Problem z Jeepem

Wykres ilości paliwa f w funkcji odległości od punktu początkowego d dla eksploracji (1–3) i przecinania (I–III) wersji problemu jeepa dla trzech jednostek paliwa – kolorowe strzałki oznaczają składy, segmenty ukośne oznaczają podróż, a segmenty pionowe oznaczają paliwo przenosić

Problem z jeepem , problem z przejściem przez pustynię lub problem z eksploracją to problem matematyczny, w którym jeep musi zmaksymalizować odległość, jaką może przebyć na pustynię przy określonej ilości paliwa. Jeep może przewozić tylko określoną i ograniczoną ilość paliwa, ale może zostawiać paliwo i zbierać paliwo na wysypiskach paliw w dowolnym miejscu na pustyni.

Problem pojawił się po raz pierwszy w IX-wiecznym zbiorze Propositiones ad Acuendos Juvenes ( Problemy z ostrzeniem młodych ), przypisywanym Alcuinowi , a zagadka dotyczyła podróżującego wielbłąda jedzącego ziarno. De viribus quantitatis (ok. 1500) Luca Pacioli również omawia ten problem. Nowoczesne leczenie zostało podane przez NJ Fine w 1947 roku.

Odmianami tego problemu są problem wielbłąda i bananów , w którym kupiec musi zmaksymalizować liczbę bananów transportowanych na rynek za pomocą wielbłąda, który żywi się bananami, problem podróżników przez pustynię , w którym wszyscy podróżni muszą dotrzeć do celu i mogą tylko wymieniają zapasy, zamiast je zostawiać, oraz problem samochodów przejeżdżających przez pustynię, które znowu mogą wymieniać tylko paliwo, ale gdzie puste samochody można porzucić. Ten ostatni problem przypomina działanie rakiety wielostopniowej .

Problem

Narysuj w skali problem z jeepem w wersji Exploring (góra) i Crossing (dół) dla trzech jednostek paliwa. Oś pozioma oznacza odległość, a oś pionowa czas. Pionowe kolorowe segmenty linii oznaczają zapas paliwa, a poziome oznaczają podróż z pobranym paliwem. Kolorowe cyfry oznaczają jednostki paliwa zgromadzone w danym momencie.

jest n jednostek paliwa. Jeep może przewieźć maksymalnie 1 jednostkę paliwa w dowolnym momencie i przejechać 1 jednostkę odległości na 1 jednostce paliwa (zakłada się, że zużycie paliwa przez jeepa jest stałe). W dowolnym momencie podróży jeep może zostawić dowolną ilość paliwa, którą przewozi na wysypisku paliw, lub może zebrać dowolną ilość paliwa pozostawioną na wysypisku podczas poprzedniej podróży, o ile jego ładunek nigdy nie przekracza 1 jednostka. Istnieją dwa warianty problemu:

Eksploracja pustyni – jeep musi wracać do bazy na koniec każdej wyprawy.
Przeprawa przez pustynię – jeep musi wracać do bazy na koniec każdej wyprawy, z wyjątkiem ostatniej wyprawy, kiedy jeep przejeżdża jak najdalej, zanim skończy mu się paliwo.

W obu przypadkach celem jest maksymalizacja odległości przebytej przez jeepa podczas jego ostatniej podróży. Alternatywnie, celem może być znalezienie najmniejszej ilości paliwa potrzebnej do wykonania ostatniej podróży na określoną odległość.

Wariacje

W klasycznym problemie paliwo w jeepie i na składowiskach jest traktowane jako ilość ciągła . Zaproponowano bardziej złożone warianty problemu, w których paliwo można pozostawić lub zebrać tylko w dyskretnych ilościach.

W problemie wielbłąda i bananów kupiec ma n jednostek bananów. Wielbłąd może przenosić maksymalnie 1 jednostkę bananów w dowolnym momencie i może przebyć 1 jednostkę odległości na 1 jednostce bananów. Rynek jest oddalony o m jednostek odległości. W dowolnym momencie wycieczki wielbłąd może zostawić dowolną ilość bananów, które niesie na stanowisku obozowym, lub może zebrać dowolną ilość bananów pozostawionych na stanowisku obozowym podczas poprzedniej wycieczki, o ile ładunek bananów nigdy nie przekracza 1 jednostka. Zadanie polega na określeniu maksymalnej liczby bananów, które można przetransportować na rynek.

W problemie podróżników przez pustynię baza początkowa ma nieograniczoną liczbę jednostek zaopatrzenia. Każdy podróżnik może nieść maksymalnie 1 jednostkę zaopatrzenia w dowolnym momencie i może przebyć 1 jednostkę odległości na 1 jednostce zaopatrzenia. Druga baza znajduje się na m jednostki odległości. W przeciwieństwie do dwóch poprzednich problemów, podróżnicy nie mogą zostawiać zapasów na pustyni; Jednak w dowolnym momencie podróży towarzyszący podróżnicy mogą przekazywać sobie zaopatrzenie, o ile żaden podróżnik nigdy nie przewozi więcej niż 1 jednostkę zaopatrzenia. Każdy powracający podróżnik musi mieć wystarczającą ilość zapasów w drodze powrotnej. Problem dotyczy minimalnej liczby podróżnych towarzyszących potrzebnych do dotarcia do drugiej bazy. Wariant tego problemu podaje całkowitą liczbę dostępnych podróżnych i pyta o maksymalną odległość, jaką można osiągnąć.

W samochodach przez pustynię baza startowa ma nieograniczoną liczbę jednostek paliwa. Każdy samochód może przewozić maksymalnie 1 jednostkę zaopatrzenia w dowolnym momencie i może przebyć 1 jednostkę odległości na 1 jednostce paliwa. Druga baza znajduje się na m jednostki odległości. Samochody nie mogą zostawiać paliwa na pustyni; Jednak w dowolnym momencie podróży towarzyszące samochody mogą przekazywać paliwo między sobą, o ile żaden samochód nigdy nie przewozi więcej niż 1 jednostkę paliwa. Puste samochody bez paliwa są porzucane na pustyni. Problem dotyczy minimalnej liczby samochodów towarzyszących potrzebnych do dotarcia do drugiej bazy. Wariant tego problemu podaje całkowitą liczbę dostępnych samochodów i pyta o maksymalną odległość, jaką można osiągnąć.

Rozwiązanie

Rozwiązanie wariantu „eksploracji pustyni” dla n = 3, pokazujące zawartość paliwa w jeepie i zrzuty paliwa na początku każdej podróży iw punkcie zwrotnym każdej podróży.

Strategia maksymalizująca dystans przebyty w ostatniej podróży dla wariantu „eksploracja pustyni” jest następująca:

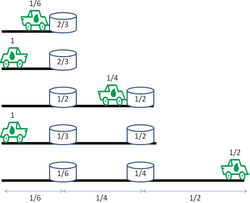
Jeep wykonuje n podróży. W każdej podróży startuje z bazy z 1 jednostką paliwa.
Podczas pierwszej podróży jeep pokonuje odległość 1/(2 n ) jednostek i zostawia ( n − 1)/ n jednostek paliwa na wysypisku paliw. Jeep ma jeszcze 1/(2 n ) jednostek paliwa – wystarczy na powrót do bazy.
Podczas każdej z kolejnych n − 1 podróży jeep zbiera 1/(2 n ) jednostek paliwa z tego pierwszego wysypiska paliwa w drodze do wyjścia, tak że wyjeżdża z wysypiska z 1 jednostką paliwa. Pobiera również 1/(2 n ) jednostek paliwa z tego pierwszego zrzutu paliwa w drodze powrotnej, co jest wystarczającą ilością paliwa na powrót do bazy.
Podczas drugiej podróży jeep jedzie do pierwszego zrzutu paliwa i tankuje. Następnie pokonuje odległość 1/(2 n − 2) jednostek i zostawia ( n − 2)/( n − 1) jednostek paliwa na drugim wysypisku paliwa. Jeep ma jeszcze 1/(2 n − 2) jednostek paliwa, co w zupełności wystarczy na powrót do pierwszego składowiska paliwa. Tutaj zbiera 1/(2 n ) jednostek paliwa, co wystarczy na powrót do bazy.
Podczas każdej z kolejnych n − 2 podróży jeep zbiera 1/(2 n − 2) jednostek paliwa z tego drugiego wysypiska paliwa w drodze na zewnątrz, tak że wyjeżdża z wysypiska z 1 jednostką paliwa. Pobiera również 1/(2 n − 2) jednostek paliwa z drugiego zrzutu paliwa w drodze powrotnej, co jest wystarczającą ilością paliwa, aby wrócić do pierwszego zrzutu paliwa.
Jeep porusza się w ten sposób, że podczas podróży k ustanawia nowy k -ty zrzut paliwa w odległości 1/(2 n − 2 k + 2) jednostek od poprzedniego zrzutu paliwa i odjeżdża ( n − k )/( n − k + 1) jednostki paliwa tam. Podczas każdego z kolejnych n − k przejazdów zbiera 1/(2 n − 2 k + 2) jednostek paliwa z k- tego składowiska w drodze na zewnątrz i kolejną 1/(2 n − 2 k + 2) jednostki paliwa w drodze powrotnej.

Kiedy jeep rozpoczyna ostatnią podróż, jest n − 1 zrzutów paliwa. Najdalszy zawiera 1/2 jednostki paliwa, następny najdalszy zawiera 1/3 jednostki paliwa itd., a na najbliższym wysypisku paliwa pozostała tylko 1/ n jednostek paliwa. Razem z 1 jednostką paliwa, z jaką startuje z bazy, oznacza to, że jeep może przebyć w obie strony całkowity dystans

{\ Displaystyle 1 + {\ Frac {1} {2}} + { \frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}}\equiv 2\ razy \mathrm {eksploracja} (n)}

jednostek podczas ostatniej podróży (maksymalna odległość przebyta na pustynię to połowa tej odległości). Po drodze zbiera połowę pozostałego paliwa na każdym wysypisku, co zapełnia jego zbiornik. Po opuszczeniu najdalszego wysypiska paliwa przemieszcza się 1/2 jednostki dalej w głąb pustyni, a następnie wraca do najdalszego wysypiska paliwa. W drodze powrotnej zbiera pozostałe paliwo z każdego zrzutu paliwa, które wystarczy na dotarcie do następnego zrzutu paliwa lub, w ostatnim kroku, na powrót do bazy.

Rozwiązanie wariantu „przekraczania pustyni” dla n = 3, pokazujące zawartość paliwa w jeepie i zrzuty paliwa na początku każdej podróży, w punkcie zwrotnym podczas pierwszych dwóch podróży i na końcu ostatniej podróży.

Dystans przebyty podczas ostatniej podróży to _n - ta liczba harmoniczna , Hn . Ponieważ liczby harmoniczne są nieograniczone, możliwe jest przekroczenie dowolnej odległości podczas ostatniej podróży, o ile w bazie dostępna jest wystarczająca ilość paliwa. Jednak zarówno ilość wymaganego paliwa, jak i liczba zrzutów paliwa rosną wykładniczo wraz z odległością do pokonania.

Wariant „przeprawa przez pustynię” można rozwiązać za pomocą podobnej strategii, z tą różnicą, że nie ma teraz wymogu zbierania paliwa w drodze powrotnej w ostatnią podróż. Tak więc podczas podróży k jeep zakłada nowy k- ty zrzut paliwa w odległości 1/(2 n − 2 k + 1) jednostek od poprzedniego zrzutu paliwa i opuszcza (2 n − 2 k − 1)/(2 n − 2 k + 1) jednostek paliwa tam. Na każdym z kolejnych n − k − 1 przejazdów zbiera 1/(2 n − 2 k + 1) jednostek paliwa z k- tego składowiska w drodze powrotnej i kolejnych 1/(2 n − 2 k + 1) jednostek paliwa w drodze powrotnej.

Teraz, gdy jeep rozpoczyna ostatnią podróż, jest n − 1 zrzutów paliwa. Najdalszy zawiera 1/3 jednostki paliwa, następny najdalszy zawiera 1/5 jednostki paliwa i tak dalej, a na najbliższym wysypisku paliwa pozostało tylko 1/(2 n - 1 ) jednostek paliwa. Razem z 1 jednostką paliwa, z jaką startuje z bazy, oznacza to, że jeep może przejechać łączną odległość ok

{\ Displaystyle 1 + {\ Frac {1} {3}} + {\ Frac {1} {5}} + \ cdots + {\ Frac {1} {2n-1}} = \ suma _ {k = 1 }^{n}{\frac {1}{2k-1}}=H_{2n-1}-{\frac {1}{2}}H_{n-1}\equiv \mathrm {krzyż} (n )}

jednostek w ostatnią podróż. Po drodze zbiera całe pozostałe paliwo na każdym wysypisku, które wypełnia jego zbiornik. Po opuszczeniu najdalszego wysypiska paliwa pokonuje dalszą odległość 1 jednostki.

Zauważ to

{\ Displaystyle \ operatorname {krzyż} (n) = \ suma _ {k = 1} ^ {n} {\ Frac {1} {2k-1}}> \ suma _ {k = 1} ^ {n} \frac {1}{2k}}={\frac {1}{2}}H_{n}=\mathrm {eksploracja} (n)}

więc teoretycznie możliwe jest pokonanie pustyni dowolnej wielkości, mając wystarczającą ilość paliwa w bazie. Tak jak poprzednio, wymagana ilość paliwa i liczba zrzutów paliwa rosną wykładniczo wraz z odległością do pokonania.

Podsumowując, maksymalna odległość, jaką jeep może pokonać (z zapasem paliwa na 1 jednostkę odległości w dowolnym momencie) podczas n podróży (z n-1 zrzutami paliwa w połowie drogi i zużyciem łącznie n jednostek paliwa) wynosi

${\ Displaystyle \ operatorname {eksplorować} (n) = {\ Frac {1} {2} }}H_{n}={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{6}}+\cdots +{\frac {1}{ 2n}}}$ , do eksploracji pustyni, gdzie jeep musi wracać do bazy na koniec każdej podróży;
${\ Displaystyle \ operatorname {krzyż} (n) = H_ {2n-1}-{\frac {1}{2}}H_{n-1}=1+{\frac {1}{3}}+{\frac {1}{5}}+\cdots + {\frac {1}{2n-1}}}$ , za przeprawę przez pustynię, gdzie jeep musi wracać do bazy na koniec każdej podróży, z wyjątkiem ostatniej podróży, kiedy jeep jedzie tak daleko, jak to możliwe, zanim skończy się paliwo.

$+{\frac {1}{n}}}$ ${\ Displaystyle H_ {n} = 1 + {\ Frac {1} {2}} + {\ Frac {1} {3}} + \$ cdots to n-ta liczba harmoniczna .

Stała ilość paliwa

Liczba jednostek paliwowych dostępnych w bazie nie musi być liczbą całkowitą. W ogólnym przypadku maksymalna odległość możliwa do osiągnięcia w przypadku problemu „eksploracja pustyni” przy użyciu $n$ jednostek paliwa wynosi

{\ Displaystyle \ operatorname {eksplorować} (n) = \ int _ {0} ^ {n} {\ Frac {\ operatorname {\ operatorname { d} f}{2\lceil nf\rceil }}}

z pierwszym zrzutem paliwa $znajdującym$ bazy ${\ Displaystyle 1/(2 \ lceil n \ rceil -2)}$ jednostek odległości od pierwszego zrzutu paliwa, trzeciego w ${\ Displaystyle 1 / (2 \ lceil n \ rceil -4)}$ jednostki odległości od drugiego wysypiska paliwa i tak dalej. Tutaj ${\ Displaystyle \ {n \} = n- \ lfloor n \ rfloor}$ jest częścią ułamkową $n$ .

Maksymalna odległość, jaką można osiągnąć w przypadku problemu „przekroczyć pustynię” przy użyciu $n$ jednostek paliwa, wynosi

{\ Displaystyle \ operatorname {krzyż} (n) = \ int _ {0} ^ {n} {\ Frac {\ operatorname { d} f}{2\lceil nf\rceil -1}}}

z pierwszym zrzutem paliwa znajdującym się w jednostkach odległości od bazy startowej ${\ Displaystyle \ {n \} / (2 \ lceil n \ rceil -1)}$ jeden w jednostkach odległości ${\ Displaystyle 1 / (2 \ lceil n \ rceil -3)}$ od pierwszego zrzutu paliwa, trzeci w $zrzutu$ i tak dalej. Tutaj ${\ Displaystyle \ {n \} = n- \ lfloor n \ rfloor}$ jest częścią ułamkową $n$ .

Inne warianty problemu

W problemie wielbłąda i bananów , zakładając, że kupiec ma łącznie n=7/3 jednostek bananów w bazie startowej, a rynek jest oddalony o m jednostek odległości:

Jeśli ${\ Displaystyle m> \ operatorname {krzyż} (n) = 1/15 + 1/3 + 1}$ , nie istnieje rozwiązanie dla ten problem;
Jeśli ${\ Displaystyle m \ równoważnik \ operatorname {krzyż} (n) - \ operatorname {krzyż} (\ lfloor n \rfloor )=1/15}$ , do transportu nie jest potrzebny żaden środkowy słupek obozowy, a odległość m będzie się powtarzać przez ${\ Displaystyle 2 \ lceil n \ rceil -1 = 5}$ razy przez wielbłąda, więc maksymalna ilość bananów transportowanych na rynek to $nm\times (2\lceil n\rceil -1)=7/3-5m$ ;
Jeśli ${\ Displaystyle \ operatorname {krzyż} (n) - \ operatorname {krzyż} (\ lfloor n\rfloor )<m\leq \mathrm {cross} (n)}$ $\mathrm {cross} (n)-\mathrm {cross} (\lfloor n\rfloor )<m\leq \mathrm {cross} (n)$ , optymalne rozwiązanie do transportu maksymalnej ilości bananów wymaga kilku pośrednich stanowisk obozowych:
1. Dla m=1/4<(1/3+1/15) potrzebny jest tylko jeden środkowy posterunek obozowy w odległości 1/15 jednostki od bazy startowej, gdzie łącznie zgromadzone zostaną 2 jednostki bananów. Odległość od posterunku obozowego do rynku to (1/4-1/15), którą wielbłąd powtórzy 3 razy, a maksymalna ilość bananów przewożonych na rynek to 2-(1/4-1/ 15)*3=1,45 jednostki;
2. Dla m=1/2>(1/3+1/15) potrzebny jest kolejny środkowy posterunek obozowy w odległości 1/3 jednostek od pierwszego posterunku, na którym zgromadzona zostanie w sumie 1 jednostka bananów. Odległość od drugiego posterunku obozowego do rynku to [1/2-(1/3+1/15)], którą wielbłąd przejedzie tylko raz, a maksymalna ilość bananów przewożonych na rynek to 1- [1/2-(1/3+1/15)]*1=0,9 jednostki.

Jeśli wielbłąd musi w końcu powrócić do bazy początkowej, wówczas ma zastosowanie funkcja ${\ Displaystyle \ operatorname {explore} (n)}$ (nadal zakładając n = 7/3 ):

Jeśli ${\ Displaystyle m> \ operatorname {eksplorować} (n) = 1/18 + 1/4 + 1/2 }$ , nie ma rozwiązania tego problemu;
Jeśli ${\ Displaystyle m \ równoważnik \ operatorname {eksplorować} (n) - \ operatorname {eksplorować} (\lfloor n\rfloor )=1/18}$ , do transportu nie jest potrzebne żadne stanowisko obozowe w połowie drogi, a odległość m będzie się powtarzać przez ${\ Displaystyle 2 \ lceil n \ rceil = 6}$ razy przez wielbłąda, więc maksymalna ilość bananów transportowanych na rynek to ${\ displaystyle nm \ razy (2\lceil n\rceil )=7/3-6m}$ ;
mi ${\ Displaystyle \ operatorname {eksplorować} (n) -$ $\mathrm {explore} (n)-\mathrm {explore} (\lfloor n\rfloor )<m\leq \mathrm {explore} (n)$ , optymalne rozwiązanie do transportu takiej maksymalnej ilości bananów wymaga kilku pośrednich stanowisk obozowych:
1. Dla m=1/4<(1/4+1/18) potrzebny jest tylko jeden środkowy posterunek obozowy w odległości 1/18 jednostki od bazy startowej, gdzie w sumie 2 jednostki bananów (plus 1/18 jednostek 18 jednostek za ostateczny powrót wielbłąda). Odległość od posterunku obozowego do rynku to (1/4-1/18), którą wielbłąd powtórzy 4 razy, a maksymalna ilość bananów przewożonych na rynek to 2-(1/4-1/ 18)*4=1,22 jednostki;
2. Dla m=1/2>(1/4+1/18) potrzebny jest kolejny środkowy posterunek obozowy w odległości 1/4 jednostki od pierwszego posterunku, gdzie w sumie 1 jednostka bananów (plus 1/4 jednostki na ostateczny powrót wielbłąda) zostaną naliczone. Odległość od drugiego posterunku obozowego do rynku to [1/2-(1/4+1/18)], którą wielbłąd powtórzy dwukrotnie, a maksymalna ilość bananów przewożonych na rynek to 1-[ 1/2-(1/4+1/18)]*2=0,61 jednostek.

W problemie podróżników przez pustynię załóżmy, że n podróżników wyruszyło z bazy startowej z n jednostkami zaopatrzenia. Po 1/( n +1) jednostkach odległości zużyliby już n / ( n +1) jednostek zaopatrzenia; W tym momencie jeden z podróżników powinien wrócić z 1/( n +1) jednostkami zaopatrzenia, pozostawiając grupę dokładnie ( n -1) jednostek zaopatrzenia, tak aby każdy pozostały podróżnik niósł dokładnie jedną jednostkę zaopatrzenia. Następnie grupa pokonuje kolejne 1/( n +1) jednostki odległości, zużywające ( n -1)/( n +1) jednostki zaopatrzenia; W tym momencie jeden z pozostałych podróżników powinien wrócić z 2/( n +1) jednostkami zaopatrzenia, aby bezpiecznie wrócić do bazy startowej, opuszczając grupę dokładnie ( n -2) jednostek zaopatrzenia. Grupa porusza się o 1/( n +1) jednostek odległości i zmniejsza jednego podróżnika, aż pozostanie tylko jeden podróżnik niosący dokładnie jedną jednostkę zaopatrzenia. Wreszcie, ten podróżnik może przebyć jedną jednostkę odległości, aby dotrzeć do najdalszego punktu. W sumie najdłuższa odległość, n podróżnych, wynosi

{\ Displaystyle \ operatorname {podróżować} (n) = {\ Frac {n-1} {n + 1} }+1=2-{\frac {2}{n+1}}}

Przyrównując to do m , można obliczyć minimalną liczbę podróżnych potrzebną do przebycia m jednostek odległości. Zauważ, że rozwiązania istnieją tylko dla m <2.

Jeśli ostatni i ostatni podróżnik również musi wrócić do bazy początkowej, to sam podróżowałby tylko 1/( n +1) jednostek, więc ma n /( n +1) jednostek zaopatrzenia do powrotu, więc najdłuższy dystans n podróżni mogą dotrzeć

{\ Displaystyle \ operatorname {podróż_ {powrót}} (n) = {\ Frac {n} {n +1}}=1-{\frac {1}{n+1}}}

Przyrównując to do m , można obliczyć minimalną liczbę podróżnych potrzebną do przebycia m jednostek odległości. Zauważ, że rozwiązania istnieją tylko dla m <1.

W problemie samochodów przez pustynię załóżmy, że n samochodów wyruszyło z bazy startowej z n jednostkami paliwa. Po przebyciu 1/ n jednostek odległości grupa zużyłaby już dokładnie jedną jednostkę paliwa; W tym momencie powinni przelać paliwo między sobą, zostawić pusty samochód i przewieźć ( n -1) jednostek paliwa między ( n -1) samochodami. Po przebyciu kolejnej 1/( n -1) jednostek odległości grupa zużyłaby kolejną jednostkę paliwa; Ponownie, powinni przelać paliwo, zostawić pusty samochód i nieść ( n -2) jednostek paliwa wśród ( n -2) samochodów. Grupa porusza się i zmniejsza jeden samochód, aż zostanie tylko jeden samochód z dokładnie jedną jednostką paliwa. Wreszcie, ten samochód może przebyć jedną jednostkę odległości, aby dotrzeć do najdalszego punktu. W sumie najdłuższa odległość, jaką może pokonać n samochodów, to n- ta liczba harmoniczna :

${\ Displaystyle H_ {n} = 1 + {\ Frac {1} {2}} + {\ Frac {1} {3}} + \ cdots + {\frac {1}{n}}}$

Przyrównując to do m , można znaleźć minimalną liczbę samochodów potrzebną do przebycia m jednostek odległości.

Zamów niezależność

Należy pamiętać, że kolejność wycieczek jeepem nie jest ustalona. Na przykład w wersji problemu „eksploracja pustyni” jeep mógłby wykonać $n - 1$ przejazdów w obie strony między bazą a pierwszym zrzutem paliwa, pozostawiając $(n - 1) / n$ jednostek paliwa na zrzucie paliwa za każdym razem a następnie wykonaj $n$ -tą podróż w jedną stronę do pierwszego zrzutu paliwa, docierając tam w sumie z $(n - 1) + 1/(2 n)$ dostępnymi jednostkami paliwa. 1 $/(2 n)$ jednostki są zapisywane na podróż powrotną do bazy na samym końcu, a pozostałe $n - 1$ jednostki paliwa są wykorzystywane do przemieszczania paliwa między pierwszym a drugim zrzutem paliwa, przy użyciu $n - 2$ podróży w obie strony, a następnie $(n -1)$ -ty przejazd w jedną stronę do drugiego zrzutu paliwa. I tak dalej.

Praktyczne zastosowania

Podczas operacji Black Buck One atakujący Vulcan był tankowany siedem razy w drodze powrotnej i raz w drodze powrotnej. Szare linie wskazują samoloty rezerwowe, które mają zastąpić ofiary.

Problem może mieć praktyczne zastosowanie w sytuacjach wojennych, zwłaszcza w odniesieniu do efektywności paliwowej . W kontekście bombardowania Japonii w czasie II wojny światowej przez B-29 , Robert McNamara mówi w filmie The Fog of War , że zrozumienie problemu zużycia paliwa spowodowanego koniecznością transportu paliwa do baz wysuniętych było głównym powodem, dla którego strategia od rozpoczęcia nalotów bombowych z Chin kontynentalnych zrezygnowano na rzecz strategii skakania po wyspach :

„Musieliśmy lecieć tymi samolotami z baz w Kansas do Indii. Potem musieliśmy lecieć paliwem przez garb do Chin. […] Mieliśmy wziąć te B-29 - nie było tam żadnych tankowców . mieli napełnić je paliwem, lecieć z Indii do Chengtu ; rozładować paliwo; lecieć z powrotem do Indii; odbyć wystarczającą liczbę misji, aby zgromadzić paliwo w Chengtu; lecieć do Yawata w Japonii ; zbombardować huty ; i wrócić do Indii. Mieliśmy tak mało szkoleń w zakresie maksymalizacji wydajności [paliwa], że faktycznie odkryliśmy, że zamiast wyładowywać paliwo, odzyskali część B-29, musieli się tym zająć. Krótko mówiąc, nie było to nic warte. I to LeMay naprawdę doszedł do tego wniosku i doprowadził szefów do przeniesienia całej sprawy na Mariany , które spustoszyły Japonię”.

( Misje bomb atomowych pod koniec II wojny światowej odbywały się przy użyciu B-29 Superfortress z wyspy Tinian na Pacyfiku na Marianach Północnych ).

Zobacz także Operację Black Buck , aby zapoznać się z zastosowaniem tych pomysłów. W tych misjach, prowadzonych podczas wojny o Falklandy , Królewskie Siły Powietrzne wykorzystywały tankowanie powietrze-powietrze przez tankowce, aby umożliwić bombowcom Vulcan stacjonującym na Wyspie Wniebowstąpienia bombardowanie celów na Falklandach .

Zobacz też