Sekwencja Fareya

Diagram Fareya do F ₉ przedstawiony za pomocą okrągłych łuków. Na obrazie SVG najedź kursorem na krzywą, aby wyróżnić ją i jej elementy.

Diagram Fareya do F ₉ .

Symetryczny wzór utworzony przez mianowniki ciągu Fareya, F ₉ .

Symetryczny wzór utworzony przez mianowniki ciągu Fareya, F ₂₅ .

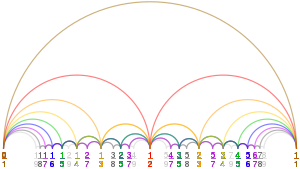
W matematyce ciąg Fareya rzędu n jest ciągiem całkowicie zredukowanych ułamków , albo od 0 do 1, albo bez tego ograniczenia, które w najniższych wartościach mają mianowniki mniejsze lub równe n , ułożone w kolejności rosnącej wielkości.

Przy ograniczonej definicji każda sekwencja Fareya zaczyna się od wartości 0, oznaczonej ułamkiem 0 / 1 , a kończy wartością 1, oznaczoną przez ułamek 1 / 1 (chociaż niektórzy autorzy pomijają te terminy).

Sekwencja Fareya jest czasami nazywana serią Fareya , co nie jest do końca poprawne, ponieważ wyrazy nie są sumowane.

Przykłady

Sekwencje Fareya rzędów od 1 do 8 to:

fa ₁ = { 0 1 _, 1 1 }

fa ₂ = { 0 1 _, 1 2 _, 1 1 }

fa ₃ = { 0 1 _, 1 3 _, 1 2 _, 2 3 _, 1 1 }

fa ₄ = { 0 1 _, 1 4 _, 1 3 _, 1 2 _, 2 3 _, 3 4 _, 1 1 }

fa ₅ = { 0 1 _, 1 5 _, 1 4 _, 1 3 _, 2 5 _, 1 2 _, 3 5 _, 2 3 _, 3 4 _, 4 5 _, 1 1 }

_, 5 6 _, 1 1 fa ₆ = { 0 1 _, 1 6 _, 1 5 _, 1 4 _, 1 3 _, 2 5 _, 1 2 _, 3 5 _, 2 3 _, 3 4 _, 4 } 7

_, 1 1 fa ₇ = { 0 1 _, 1 6 _, / 5 _, 1 4 _, 2 7 _, 1 3 _, 2 5 _, 3 7 _, 1 2 _, 4 7 _, 3 5 _, 2 3 _, 5 4 / 6 5 7 _,₃_, 4 5 _, 6 7 _, 1 1 }

fa ₈ = { 0 1 _, 1 8 _, 1 7 _, 1 6 _, 1 5 _, 1 4 _, 2 7 _, 1 3 _, 3 8 _, 2 5 _, 3 7 _, 1 2 _, 4 7 _, 3 5 _, 5 8 _, 2 3 _, 5 7 _, 3 4 _, 4 6 5 8 _, 5 6 _, 7 7 _/_, 1 1 }

wyśrodkowany
fa ₁ = { 0 / 1 _, 1 / 1 }
fa ₂ = { 0 / 1 _, 1 / 2 _, 1 / 1 }
fa ₃ = { 0 / 1 _, 1 / 3 _, 1 / 2 _, 2 / 3 _, 1 / 1 }
fa ₄ = { 0 / 1 _, 1 / 4 _, 1 / 3 _, 1 / 2 _, 2 / 3 _, 3 / 4 _, 1 / 1 }
fa ₅ = { 0 / 1 _, 1 / 5 _, 1 / 4 _, 1 / 3 _, 2 / 5 _, 1 / 2 _, 3 / 5 _, 2 / 3 _, 3 / 4 _, 4 / 5 _, 1 / 1 }
fa ₆ = { 0 / 1 _, 1 / 6 _, 1 / 5 _, 1 / 4 _, 1 / 3 _, 2 / 5 _, 1 / 2 _, 3 / 5 _, 2 / 3 _, 3 / 4 _, 4 / 5 _, 5 / 6 _, 1 / 1 }
fa ₇ = { 0 / 1 _, 1 / 7 _, 1 / 6 _, 1 / 5 _, 1 / 4 _, 2 / 7 _, 1 / 3 _, 2 / 5 _, 3 / 7 _, 1 / 2 _, 4 / 7 _, 3 / 5 _, 2 / 3 _,₅ 3 / 7 _, / 4 4 _, / 5 , 5 / 6 _, 6 / 7 _, 1 / 1 }
fa ₈ = { 0 / 1 _, 1 / 8 _, 1 / 7 _, 1 / 6 _, 1 / 5 _, 1 / 4 _, 2 / 7 _, 1 / 3 _, 3 / 8 _, 2 / 5 _, 3 / 7 _, 1 / 2 _, 4 / 7 _, 3 / 5 _, 5 / 8 _, 2 / 3 _, 5 / 7 _, 3 / 4 _, 4 / 6 / / 8 ₅_, 5 , 6 _/ 7 , 7 _, 1 / 1 }

Posortowane

 F1 = {0/1, 1/1} F2 = {0/1, 1/2, 1/1} F3 = {0/1, 1/3, 1/2, 2/3, 1/1} F4 = {0/1, 1/4, 1/3, 1/2, 2/3, 3/4, 1/1} F5 = {0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1} F6 = {0/1, 1/6, 1/5, 1/4, 1/3 , 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, 1/1} F7 = {0/1, 1/7, 1/6, 1/ 5, 1/4, 2/7, 1/3, 2/5, 3/7, 1/2, 4/7, 3/5, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 1/1} F8 = {0/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8 , 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7 /8, 1/1}

Wybuch słońca Fareya

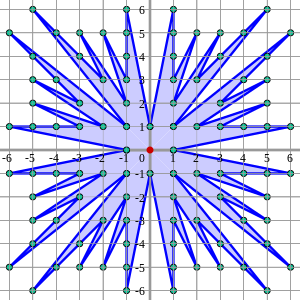
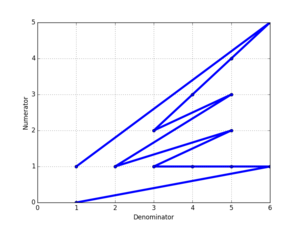
Wykreślanie liczników F _{6 w funkcji mianowników}

Rozbłyski gwiazd iteracji 1–10 nałożone na siebie

Wykreślenie liczników w funkcji mianowników sekwencji Fareya daje kształt podobny do tego po prawej, pokazanego dla $F$ ₆ .

Odzwierciedlenie tego kształtu wokół przekątnej i głównej osi generuje rozbłysk słońca Fareya , pokazany poniżej. Rozbłysk słońca Fareya rzędu $n$ łączy widoczne punkty siatki liczb całkowitych od początku w kwadracie o boku 2 $n$ , wyśrodkowanym w początku. Korzystając z twierdzenia Picka , pole rozbłysku wynosi 4 (| $F$ _n |−1), gdzie | $F$ _n | jest liczbą ułamków w $F$ _n .

Rozbłysk słońca Fareya rzędu 6, z 1 wewnętrznym (czerwonym) i 96 punktami granicznymi (zielonymi), co daje obszar 1 + 96 2 - 1 = 48, zgodnie z twierdzeniem Picka

Historia

Historia „szeregu Fareya” jest bardzo ciekawa — Hardy i Wright (1979)

... po raz kolejny człowiek, którego imię zostało nadane relacji matematycznej, nie był pierwszym odkrywcą, jeśli chodzi o zapisy. — Beiler (1964)

Sekwencje Fareya zostały nazwane na cześć brytyjskiego geologa Johna Fareya seniora , którego list o tych sekwencjach został opublikowany w Philosophical Magazine w 1816 roku. . List Fareya został odczytany przez Cauchy'ego , który przedstawił dowód w swoim Exercices de mathématique i przypisał ten wynik Fareyowi. W rzeczywistości inny matematyk, Charles Haros , opublikował podobne wyniki w 1802 roku, których nie znał ani Farey, ani Cauchy. Tak więc był to historyczny wypadek, który połączył imię Fareya z tymi sekwencjami. To jest przykład prawa eponimii Stiglera .

Nieruchomości

Diagram Fareya linii rzeczywistej do rzędu 5. Punkt w nieskończoności to 1/0.

Długość ciągu i indeks ułamka

Sekwencja Fareya rzędu n zawiera wszystkich członków sekwencji Fareya niższych rzędów. W szczególności F _n zawiera wszystkich członków F _{n −1} , a także zawiera dodatkowy ułamek dla każdej liczby mniejszej od n i względnie pierwszej do n . Zatem F ₆ 5/6 składa z 1/6 się . z F ₅ wraz ułamkami i

Środkowy wyraz ciągu Fareya F _n wynosi zawsze 1/2 ( F , dla n > 1. Z tego możemy powiązać długości F _n i _{n -1} za pomocą funkcji totient Eulera $n)}$ ${\ Displaystyle \ varphi$ :

{\ Displaystyle | F_ {n} | = | F_ {n-1} | + \ varphi (n).}

Wykorzystując fakt, że | F ₁ | = 2, możemy wyprowadzić wyrażenie na długość F _n :

{\ Displaystyle | F_ {n} | = 1 + \ suma _ {m = 1} ^ {n} \ varphi (m) = 1+\Fi (n),}

gdzie ${\ Displaystyle \ Phi (n)}$ jest totientem podsumowującym .

Mamy też :

{\ Displaystyle | F_ {n} | = {\ Frac {1} {2}} \ lewo (3 + \ suma _ {d=1}^{n}\mu (d)\left\lfloor {\tfrac {n}{d}}\right\rfloor ^{2}\right),}

i według wzoru inwersji Möbiusa :

\ Displaystyle | F_ {n} | = {\ Frac {1} {2}} (n + 3) n - \ suma _ {d = 2} ^ {n} | F _ {\ lfloor n/d \ rfloor }|,}

gdzie µ ( $podłogi$ ) jest funkcją z liczbową i jest funkcją

Asymptotyczne zachowanie | F _n | Jest :

{\ Displaystyle | F_ {n} | \ sim {\ Frac {3n ^ {2}} {\ pi ^ {2}}}.}

Indeks ${\ Displaystyle I_ {n} (a_ {k, n}) = k}$ ułamka w Farey ${\ Displaystyle a_ {k, n}}$ sekwencja ${\ Displaystyle F_ {n} = \ {a_ {k, n}: k = 0,1 \ ldots, m_ {n} \}}$ to po prostu pozycja, którą zajmuje w sekwencji $\ displaystyle a_ {k, n}} .$ Ma to szczególne znaczenie, ponieważ jest używane w alternatywnym sformułowaniu hipotezy Riemanna , patrz poniżej . Następują różne przydatne właściwości:

{\ Displaystyle I_ {n} (0/1) = 0,}

{\ Displaystyle I_ {n} (1/n) = 1,}

{\ Displaystyle I_ {n} (1/2) = (| F_ {n} | -1)/2,}

{\ Displaystyle I_ {n} (1/1) = | F_ {n} | -1,}

{\ Displaystyle I_ {n} (h / k) = | F_ {n} | -1-I_ {n} ((kh) / k).}

Indeks ${\ Displaystyle 1/k}$ gdzie ${\ Displaystyle n/(i + 1) <k \ równoważnik n/i}$ i ${\ Displaystyle n}$ jest najmniejszą wspólną wielokrotnością pierwszych $\$ , $Displaystyle n = {\ rm {lcm}} ([2, i])}$ , jest dany przez:

{\ Displaystyle I_ {n} (1/k) = 1 + n \ suma _ {j = 1} ^ {i} {\ Frac {\ varphi (j)} {j}} -k \ Phi (i). }

Fajni sąsiedzi

Ułamki, które są sąsiadującymi terminami w dowolnej sekwencji Fareya, są znane jako para Fareya i mają następujące właściwości.

Jeśli a / b i c / d są sąsiadami w sekwencji Fareya, z a / b < c / d , to ich różnica c / d - a / b jest równa 1 / bd . Od

{\ Displaystyle {\ Frac {c} {d}} - {\ Frac {a} {b}} = {\ Frac {bc-ad} {bd

jest to równoważne z powiedzeniem tego

{\ displaystyle bc-ad = 1}

.

Zatem 1/3 ich różnica i 2/5 wynosi . 1/15 są sąsiadami w F ₅ , a

Odwrotność jest również prawdziwa. Jeśli

{\ displaystyle bc-ad = 1}

dla dodatnich liczb całkowitych a , b , c i d z a < b i c < d wtedy a / b i c / d będą sąsiadami w sekwencji Fareya rzędu max( b, d ).

Jeśli p / q ma sąsiadów a / b i c / d w jakiejś sekwencji Fareya, z

\ Displaystyle {\ Frac {a} {b} < {\ Frac {p} {q} <{\ Frac {c} {d}}}

wtedy p / q jest medianą a , / b i c / d – innymi słowy

{\ Displaystyle {\ Frac {p} {q}} = {\ Frac {a + c} {b + d}}.}

Wynika to łatwo z poprzedniej własności, ponieważ jeśli bp – aq = qc – pd = 1 , to bp + pd = qc + aq , p ( b + d ) = q ( a + c ) , p / q = a + c / b + re .

Wynika z tego, że jeśli a / b i c / d są sąsiadami w sekwencji Fareya, to pierwszym wyrazem, który pojawia się między nimi, gdy zwiększa się kolejność sekwencji Fareya, jest

{\ Displaystyle {\ Frac {a + c} {b + d}},}

która po raz pierwszy pojawia się w sekwencji Fareya rzędu b + d .

Zatem pierwszym wyrazem, który 2/5 pojawia w który się a między _1/3 jest 3/8 się . , pojawia F8

Całkowita liczba par sąsiadów Fareya w _Fn wynosi 2| Fn _{_} | − 3.

Sterna -Brocota to struktura danych pokazująca, w jaki sposób sekwencja jest budowana z 0 (= 0 / 1 ) i 1 (= 1 / 1 ), biorąc kolejne mediany.

Interpretacja obszaru równoważnego

Każda kolejna para wymiernych Fareya ma równoważne pole 1. Zobacz to, interpretując kolejne wymierne r ₁ = p / q i r ₂ = p ′/ q ′ jako wektory ( p , q ) na płaszczyźnie x – y. Pole A ( p / q , p ′/ q ′) jest określone przez qp ′ − q ′ p . Ponieważ każdy dodany ułamek między dwoma poprzednimi kolejnymi ułamkami ciągu Fareya jest obliczany jako mediana (⊕), to A ( r ₁ , r ₁ ⊕ r ₂ ) = A ( r ₁ , r ₁ ) + A ( r ₁ , r ₂ ) = A ( r ₁ , r ₂ ) = 1 (ponieważ r ₁ = 1/0 i r ₂ = 0/1, jego powierzchnia musi wynosić 1).

Farey sąsiedzi i ułamki ciągłe

Ułamki, które pojawiają się jako sąsiedzi w sekwencji Fareya, mają ściśle powiązane ciągłe ekspansje ułamków. Każdy ułamek ma dwa ciągłe rozwinięcia ułamkowe — w jednym końcowy wyraz wynosi 1; w drugim końcowy wyraz jest większy niż 1. Jeśli p / q , które po raz pierwszy pojawia się w sekwencji Fareya F _q , ma ciągłe rozwinięcia ułamkowe

[0; za ₁ , za ₂ , ..., za _{n - 1} , za _n , 1]

[0; za ₁ , za ₂ , ..., za _{n - 1} , za _n + 1]

wtedy najbliższy sąsiad p / q w F _q (który będzie jego sąsiadem z większym mianownikiem) ma ciągłą ekspansję ułamkową

[0; za ₁ , za ₂ , ..., za _n ]

a jego drugi sąsiad ma ciągłą ekspansję ułamkową

[0; za ₁ , za ₂ , ..., za _{n - 1} ]

Na przykład 3/8 ma ; dwa ciągłe rozwinięcia ułamków [0 2, 1, 1, 1] i [0; 2, 1, 2] , a jego sąsiadami w F ₈ są 2 / 5 , które można rozwinąć jako [0; 2, 1, 1] ; i 1/3 [ 3 , które można rozwinąć jako [0; 2, 1].

Ułamki Fareya i najmniejsza wspólna wielokrotność

Lcm można wyrazić jako iloczyny ułamków Fareya jako

{\ Displaystyle {\ tekst {lcm}} [1,2,. ..,N]=e^{\psi (N)}={\frac {1}{2}}\left(\prod _{r\in F_{N},0<r\leq 1/2} 2\sin(\pi r)\prawo)^{2}}

gdzie jest drugą funkcją Czebyszewa . ${\ Displaystyle \ psi (N)}$

Ułamki Fareya i największy wspólny dzielnik

Ponieważ funkcja totient Eulera jest bezpośrednio połączona z gcd , tak samo jest z liczbą elementów w F _n ,

{\ Displaystyle | F_ {n} | = 1 + \ suma _ {m = 1} ^ {n} \ varphi (m) = 1 + \ suma \ limity _ {m = 1} ^ {n} \ suma \ limity _{k=1}^{m}\gcd(k,m)\cos {2\pi {\frac {k}{m}}}.}

Dla dowolnych 3 ułamków Fareya a / b , c / d i e / f zachodzi następująca identyczność między gcd wyznaczników macierzy 2x2 w wartości bezwzględnej:

{\ Displaystyle \ gcd \ lewo ({\ rozpocząć {Vmatrix} a & c \\ b & d \ koniec {Vmatrix}}, {\ zacząć {Vmatrix} a & e \\ b & f \ koniec {Vmatrix}} \ prawej) = \ gcd \ lewo ( {\begin{Vmatrix}a&c\\b&d\end{Vmatrix}},{\begin{Vmatrix}c&e\\d&f\end{Vmatrix}}\right)=\gcd \left({\begin{Vmatrix}a&e\ \b&f\end{Vmatrix}},{\begin{Vmatrix}c&e\\d&f\end{Vmatrix}}\right)}

Aplikacje

Sekwencje Fareya są bardzo przydatne do znajdowania racjonalnych przybliżeń liczb niewymiernych. Na przykład konstrukcja Eliahou dolnej granicy długości nietrywialnych cykli w procesie 3 x + 1 wykorzystuje sekwencje Fareya do obliczenia dalszego ułamkowego rozszerzania logarytmu liczby ₂ (3).

W systemach fizycznych ze zjawiskami rezonansu sekwencje Fareya zapewniają bardzo elegancką i wydajną metodę obliczania lokalizacji rezonansu w 1D i 2D.

Sekwencje Fareya są widoczne w badaniach planowania ścieżek pod dowolnym kątem na siatkach o kwadratowych komórkach, na przykład w charakteryzowaniu ich złożoności obliczeniowej lub optymalności. Połączenie można rozpatrywać w kategoriach r ograniczonych ścieżek, a mianowicie $ścieżek$ składających się z segmentów linii, z których każdy przechodzi przez co najwyżej wiersze $i$ co najwyżej kolumny Q { $Displaystyle 1 \ równoważnik q$ $Displaystyle Q}$ zbiorem wektorów takich, że $\$ równoważnik ${ \ displaystyle 0 \ równoważnik p \ równoważnik q}$ i ${\ displaystyle p}$ , ${\ displaystyle q}$ są względnie pierwsze. Niech $displaystyle Q *}$ $\$ będzie wynikiem odzwierciedlenia w linii ${\ displaystyle y = x$ } Niech ${\ Displaystyle S = \ {(\ pm x, \ pm y): (x, y) \ w Q \ kubek Q*\}}$ . Wtedy dowolną r można opisać jako sekwencję wektorów z ${\ displaystyle S}$ . ${\ displaystyle Q}$ $a$ sekwencją rzędu określoną przez odwzorowanie na ${\ Displaystyle (q, p)}$ ${\ displaystyle {\ tfrac {} p}{q}}}$ .

kręgi Forda

Porównanie okręgów Forda i diagramu Fareya z łukami kołowymi dla n od 1 do 9. Każdy łuk przecina odpowiadające mu okręgi pod kątem prostym. Na obrazie SVG najedź kursorem na okrąg lub krzywą, aby podświetlić je i ich elementy.

Istnieje związek między sekwencją Fareya a kręgami Forda .

Dla każdego ułamka p / q (w najmniejszym wyrażeniu) istnieje koło Forda C[ p / q ], które jest kołem o promieniu 1/(2 q ² ) i środku w punkcie ( p / q , 1 / 2 q ² ). Dwa okręgi Forda dla różnych ułamków są albo rozłączne , albo styczne do siebie - dwa koła Forda nigdy się nie przecinają. Jeśli 0 < p / q < 1, to okręgi Forda, które są styczne do C [ p / q ], są dokładnie okręgami Forda dla ułamków sąsiadujących z p / q w pewnym ciągu Fareya.

Zatem C [ 2 / 5 ] jest styczna do C [ 1 / 2 ], C [ 1 / 3 ], C [ 3 / 7 ], C [ 3 / 8 ] itd.

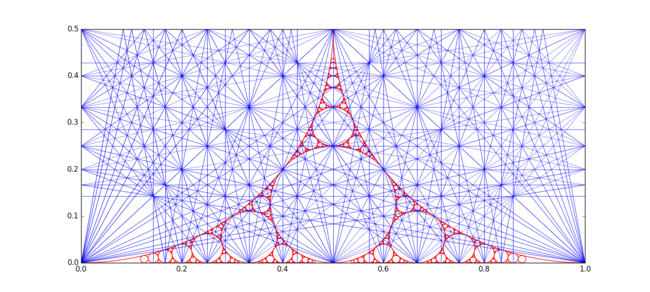
Kręgi Forda pojawiają się również w uszczelce apollińskiej (0,0,1,1). Poniższy rysunek ilustruje to wraz z liniami rezonansowymi Fareya.

Uszczelka apollińska (0,0,1,1) i wykres rezonansu Fareya.

Hipoteza Riemanna

Sekwencje Fareya są używane w dwóch równoważnych sformułowaniach hipotezy Riemanna . $: k = 0,1, \ ldots ,m_{n}\}}$ $=$ , 1 . re ${\ Displaystyle d_ {k, n} = a_ {k, n} -k/m_ {n}}$ innymi słowy ${\ Displaystyle d_{k,n}}$ jest różnicą między k -tym wyrazem n -tego ciągu Fareya, a k -tym elementem zbioru o tej samej liczbie punktów, rozłożonych równomiernie w przedziale jednostkowym. W 1924 roku Jérôme Franel udowodnił to stwierdzenie

{\ Displaystyle \ suma _ {k = 1} ^ {m_ {n}} d_ {k, n} ^ {2} =O(n^{r})\quad \forall r>-1}

jest równoważne z hipotezą Riemanna, a następnie Edmund Landau zauważył (zaraz po artykule Franela), że stwierdzenie

{\ Displaystyle \ suma _ {k = 1} ^ {m_ {n}} | d_ {k, n} | = O (n ^ {r}) \ quad \ dla wszystkich r>1/2}

jest również równoważne z hipotezą Riemanna.

Inne sumy obejmujące ułamki Fareya

Suma wszystkich ułamków Fareya rzędu n to połowa liczby elementów:

{\ Displaystyle \ suma _ {r \ w F_ {n}} r = {\ Frac {1} {2}} | F_ {n} |.}

Suma mianowników w sekwencji Fareya jest dwukrotnie większa od sumy liczników i odnosi się do funkcji totient Eulera:

{\ Displaystyle \ suma _ {a/b \ w F_ {n}} b =2\suma _{a/b\in F_{n}}a=1+\suma _{i=1}^{n}i\varphi (i),}

co zostało przypuszczane przez Harolda L. Aarona w 1962 r. i zademonstrowane przez Jeana A. Blake'a w 1966 r. Jednowierszowy dowód hipotezy Harolda L. Aarona jest następujący. Suma liczników wynosi ${\ Displaystyle {\ Displaystyle 1 + \ suma _ { 2\równoważnik b\równoważnik n}\sum _{(a,b)=1}a=1+\sum _{2\równoważnik b\równoważnik n}b{\frac {\varphi (b)}{2} }}}$ . Suma mianowników to ${\ Displaystyle {\ Displaystyle 2 + \ suma _ {2 \ równoważnik b\równoważnik n}\sum _{(a,b)=1}b=2+\sum _{2\równoważnik b\równoważnik n}b\varphi (b)}}$ . Iloraz pierwszej sumy przez drugą sumę wynosi ${\ Displaystyle {\ Frac {1} {2}}}$ .

Niech b _j będą uporządkowanymi mianownikami F _n , wtedy:

{\ Displaystyle \ suma _ {j = 0} ^ {| F_ {n} | -1} {\ Frac {b_ {j}}} {b_ {j + 1}}} = {\ Frac {3 | F_{n}|-4}{2}}}

I

{\ Displaystyle \ suma _ {j = 0} ^ {| F_ {n} | -1} {\ Frac {1} {b_ {j + 1} b_ {j }}}=1.}

Niech a _j / b _{j będzie} zatem j - tym ułamkiem Fareya w F _n

\ Displaystyle \ suma _ {j = 1} ^ {| F_{n}|-1}(a_{j-1}b_{j+1}-a_{j+1}b_{j-1})=\suma _{j=1}^{|F_{n }|-1}{\begin{Vmatrix}a_{j-1}&a_{j+1}\\b_{j-1}&b_{j+1}\end{Vmatrix}}=3(|F_{n }|-1)-2n-1,}

co jest zademonstrowane w . Również zgodnie z tym odniesieniem termin wewnątrz sumy można wyrazić na wiele różnych sposobów:

{\ Displaystyle a_ {j-1} b_ {j + 1} -a_ {j + 1} b_ {j-1} = {\ Frac {b_ {j-1} + b_ {j + 1}} {b_{j}}}={\frac {a_{j-1}+a_{j+1}}{a_{j}}}=\left\lfloor {\frac {n+b_{j-1} }{b_{j}}}\right\rfloor ,}

uzyskując w ten sposób wiele różnych sum na elementach Fareya z tym samym wynikiem. Używając symetrii około 1/2, poprzednią sumę można ograniczyć do połowy ciągu jako

\ Displaystyle \ suma _ { j=1}^{\lpodłoga |F_{n}|/2\rpodłoga}(a_{j-1}b_{j+1}-a_{j+1}b_{j-1})=3(| F_{n}|-1)/2-n-\lceil n/2\rceil ,}

Funkcję Mertensa można wyrazić jako sumę ułamków Fareya jako

}}

\ Displaystyle M (n) = -1 + \ suma _ {a \ w {\ mathcal {F}} _ {n}} e ^ {

jest

gdzie sekwencją Fareya rzędu n .

Ta formuła jest używana w dowodzie twierdzenia Franela-Landaua .

Następny termin

Istnieje zaskakująco prosty algorytm do generowania wyrazów Fn _. w porządku tradycyjnym (rosnącym) lub nietradycyjnym (malejącym) Algorytm oblicza każdy kolejny wpis na podstawie dwóch poprzednich wpisów, korzystając z podanej powyżej właściwości mediany. Jeśli a / b i c / d to dwa podane wpisy, a p / q to nieznany następny wpis, to c / d = a + p / b + q . Ponieważ c / d jest w najniższych wyrażeniach, musi istnieć liczba całkowita k taka, że kc = a + p i kd = b + q , co daje p = kc - a i q = kd - b . Jeśli uznamy, że p i q są funkcjami k , to

{\ Displaystyle {\ Frac {p (k)} {q (k)}} - {\ Frac {

więc im większe k , tym bardziej p / q zbliża się do c / d .

Aby podać następny wyraz ciągu, k musi być jak największe, z zastrzeżeniem kd − b ≤ n (ponieważ rozważamy tylko liczby o mianownikach nie większych niż n ), więc k jest największą liczbą całkowitą ≤ n + b / d . Wstawienie tej wartości k z powrotem do równań dla p i q daje

{\ Displaystyle p = \ lewo \ lfloor {\ Frac {n + b} {d}} \ prawo \ rfloor ca}

{ \ Displaystyle q = \ lewo \ lfloor {\ Frac {n + b} {d}} \ prawo \ rfloor db}

Jest to zaimplementowane w Pythonie w następujący sposób:

        
    
         0   
     
              
     
              0  
              
                        
          def  farey_sequence  (  n  :  int  ,  maleing  :  bool  =  False  )  ->  None  :  """Wypisz n-tą sekwencję Fareya. Zezwól na rosnącą lub malejącą."""  (  a  ,  b  ,  c  ,  d  )  =  (  ,  1  ,  1  ,  n  )  jeśli  malejąco  :  (  a  ,  c  )  =  (  1  ,  n  -  1  )  print  (  "  {0}  /  {1}  "  .  format  (  a  ,  b  ))  while  (  c  <=  n  i  nie  malejąco  )  lub  (  a  >  i  malejąco  ):  k  =  (  n  +  b  )  //  re  (  a  ,  b  ,  c  ,  d  )  =  (  c  ,  re  ,  k  *  c  -  a  ,  k  *  d  -  b  )  print  (  "  { 0}  /  {1}  "  .  format  (  a  ,  b  ))

Brutalne poszukiwanie rozwiązań równań diofantycznych w liczbach wymiernych często może wykorzystywać szereg Fareya (do wyszukiwania tylko form zredukowanych). Podczas gdy ten kod wykorzystuje pierwsze dwa terminy sekwencji do zainicjowania a , b , c i d , można zastąpić dowolną parę sąsiednich terminów, aby wykluczyć te mniejsze niż (lub większe niż) określony próg.

Zobacz też

przypisy

Dalsza lektura

Hatcher, Allen . „Topologia liczb” . Matematyka. Itaka, NY: Cornell U.
Graham, Ronald L .; Knuth, Donald E .; Patashnik, Oren (1989). Matematyka konkretna: podstawa informatyki (wyd. 2). Boston, MA: Addison-Wesley. s. 115–123, 133–139, 150, 462–463, 523–524. ISBN 0-201-55802-5 . — w szczególności zob. §4.5 (s. 115–123), Bonus Problem 4.61 (s. 150, 523–524), §4.9 (s. 133–139), §9.3, Problem 9.3.6 (s. 462– 463).
Vepstas, Linas. „Znak zapytania Minkowskiego, GL (2, Z) i grupa modułowa” (PDF) . — dokonuje przeglądu izomorfizmów drzewa Sterna-Brocota.
Vepstas, Linas. „Symetrie map podwajających się okresów” (PDF) . — przegląda powiązania między ułamkami Fareya a fraktalami.
Cobeli, Krystian; Zaharescu, Alexandru (2003). „Sekwencja Harosa – Fareya po dwustu latach. Ankieta”. Acta Univ. Matematyka Apulensisa. Poinformować. (5): 1–38. „str. 1–20” (PDF) . Acta Univ. Apulensis . „str. 21–38” (PDF) . Acta Univ. Apulensis .
Matwiejew, Andriej O. (2017). Sekwencje Fareya: dualność i mapy między podsekwencjami . Berlin, DE: De Gruyter. ISBN 978-3-11-054662-0 . Errata + kod

Linki zewnętrzne

Bogomolny, Aleksander . „Seria Fareya” . Przeciąć węzeł .
Bogomolny, Aleksander . „Drzewo Stern-Brocot” . Przeciąć węzeł .
Pennestri, Ettore. „Stół Brocota o podstawie 120” .
„Seria Farey” , Encyklopedia matematyki , EMS Press , 2001 [1994]
Weisstein, Eric W. „Drzewo Sterna-Brocota” . MathWorld .
OEIS A005728 (liczba ułamków w szeregu Fareya rzędu n)
OEIS A006842 (liczniki serii Fareya rzędu n)
OEIS A006843 (mianowniki szeregu Fareya rzędu n)
Zarchiwizowane w Ghostarchive i Wayback Machine : Bonahon, Francis . Zabawne ułamki i koła Forda (wideo). Brady'ego Harana . Źródło 9 czerwca 2015 r. - przez YouTube.