Solidne modelowanie
Modelowanie bryłowe (lub modelowanie bryłowe ) to spójny zbiór zasad matematycznego i komputerowego modelowania trójwymiarowych kształtów (brył) . Modelowanie bryłowe różni się od pokrewnych obszarów modelowania geometrycznego i grafiki komputerowej , takich jak modelowanie 3D , poprzez nacisk na wierność fizyczną. Razem zasady modelowania geometrycznego i bryłowego stanowią podstawę projektowania wspomaganego komputerowo 3D i ogólnie wspierają tworzenie, wymianę, wizualizację, animację, przesłuchanie i opisywanie cyfrowych modeli obiektów fizycznych.
Przegląd
Zastosowanie technik modelowania bryłowego pozwala na automatyzację kilku trudnych obliczeń inżynierskich, które są realizowane w ramach procesu projektowania. Symulacja, planowanie i weryfikacja procesów, takich jak obróbka i montaż , były jednymi z głównych katalizatorów rozwoju modelowania bryłowego. Niedawno zakres obsługiwanych zastosowań produkcyjnych został znacznie rozszerzony o produkcję blach , formowanie wtryskowe , spawanie , rury trasowanie itp. Poza tradycyjną produkcją, techniki modelowania bryłowego stanowią podstawę szybkiego prototypowania , cyfrowej archiwizacji danych i inżynierii odwrotnej poprzez rekonstrukcję brył z próbkowanych punktów na obiektach fizycznych, analizy mechanicznej z wykorzystaniem elementów skończonych , planowania ruchu i weryfikacji ścieżki NC, kinematyki i dynamiczna analiza mechanizmów , i tak dalej. Głównym problemem we wszystkich tych zastosowaniach jest możliwość skutecznego przedstawiania trójwymiarowej geometrii i manipulowania nią w sposób zgodny z fizycznym zachowaniem prawdziwych artefaktów. Badania i rozwój w zakresie modelowania bryłowego skutecznie rozwiązały wiele z tych problemów i nadal pozostają głównym przedmiotem zainteresowania inżynierii wspomaganej komputerowo .
Podstawy matematyczne
Pojęcie modelowania bryłowego w dzisiejszej praktyce opiera się na szczególnej potrzebie kompletności informacyjnej w systemach mechanicznego modelowania geometrycznego w tym sensie, że każdy model komputerowy powinien obsługiwać wszystkie zapytania geometryczne, które można zadać w stosunku do odpowiadającego mu obiektu fizycznego. Wymaganie domyślnie uznaje możliwość kilku komputerowych reprezentacji tego samego obiektu fizycznego, o ile dowolne dwie takie reprezentacje są spójne. Niemożliwe jest obliczeniowe sprawdzenie kompletności informacyjnej reprezentacji, chyba że pojęcie obiektu fizycznego zostanie zdefiniowane w kategoriach obliczalnych właściwości matematycznych i niezależne od jakiejkolwiek konkretnej reprezentacji. Takie rozumowanie doprowadziło do rozwoju paradygmatu modelowania, który ukształtował dziedzinę modelowania bryłowego, jaką znamy dzisiaj.
Wszystkie produkowane komponenty mają skończone rozmiary i dobrze zachowane granice , dlatego początkowo skupiono się na matematycznym modelowaniu sztywnych części wykonanych z jednorodnego materiału izotropowego , który można było dodawać lub usuwać. Te postulowane właściwości można przełożyć na właściwości regionów , podzbiorów trójwymiarowej przestrzeni euklidesowej . Dwa powszechne podejścia do definiowania „solidności” opierają się odpowiednio na topologii zbiorów punktowych i topologii algebraicznej . Obydwa modele określają, w jaki sposób można zbudować bryły z prostych elementów lub komórek.
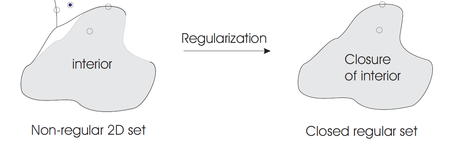
Zgodnie z kontinuum punktowym modelem solidności, wszystkie punkty dowolnego X ⊂ ℝ 3 można sklasyfikować zgodnie z ich sąsiedztwem w odniesieniu do X jako punkty wewnętrzne , zewnętrzne lub graniczne . Zakładając, że ℝ 3 posiada typową metrykę euklidesową , otoczenie punktu p ∈ X przyjmuje postać otwartej kuli . Aby X można było uznać za bryłę, każde sąsiedztwo dowolnego p ∈ X musi być konsekwentnie trójwymiarowe; punkty z sąsiedztwami o niższych wymiarach wskazują na brak solidności. Jednorodność wymiarowa otoczeń jest gwarantowana dla klasy zamkniętych zbiorów regularnych , zdefiniowanych jako zbiory równe domknięciu ich wnętrza. Dowolny X ⊂ ℝ 3 można przekształcić w zamknięty zbiór regularny lub „uregulować” poprzez domknięcie jego wnętrza, a zatem przestrzeń modelowania brył jest matematycznie zdefiniowana jako przestrzeń zamkniętych podzbiorów regularnych ℝ 3 ( przez Z twierdzenia Heinego-Borela zakłada się, że wszystkie bryły są zbiorami zwartymi ). Ponadto bryły muszą być zamknięte w ramach operacji logicznych zbioru, przecięcia i różnicy (aby zagwarantować trwałość po dodaniu i usunięciu materiału). Zastosowanie standardowych operacji boolowskich do zamkniętych zbiorów regularnych może nie dać zamkniętego zbioru regularnego, ale problem ten można rozwiązać poprzez uregulowanie wyniku zastosowania standardowych operacji boolowskich. Uregulowane operacje na zbiorach są oznaczone ∪ ∗ , ∩ ∗ i − ∗ .
Kombinatoryczna charakterystyka zbioru X ⊂ ℝ 3 jako bryły obejmuje reprezentowanie X jako orientowalnego kompleksu komórek , tak że komórki zapewniają skończone adresy przestrzenne dla punktów w skądinąd niezliczonym kontinuum. Klasa półanalitycznych ograniczonych podzbiorów przestrzeni euklidesowej jest zamknięta na operacje logiczne (standardowe i uregulowane) i wykazuje dodatkową właściwość polegającą na tym, że każdy zbiór półanalityczny można rozłożyć na zbiór rozłącznych komórek o wymiarach 0,1,2,3 . Triangulacja _ Przykładem powszechnie stosowanej stratyfikacji jest zbiór półanalityczny na zbiór punktów, odcinków linii , ścian trójkątnych i elementów czworościennych . Kombinatoryczny model solidności można następnie podsumować stwierdzeniem, że bryły są nie tylko półanalitycznie ograniczonymi podzbiorami, ale także trójwymiarowymi wielościanami topologicznymi , w szczególności trójwymiarowymi orientowanymi rozmaitościami z granicą. W szczególności implikuje to charakterystykę Eulera kombinatorycznej granicy wielościanu wynosi 2. Kombinatoryczny rozmaity model solidności gwarantuje również, że granica bryły dzieli przestrzeń na dokładnie dwie składowe zgodnie z twierdzeniem Jordana-Brouwera, eliminując w ten sposób zbiory z nierozmaitymi otoczeniami, które są uważane niemożliwe do wytworzenia.
Modele punktowe i kombinatoryczne brył są ze sobą całkowicie spójne, można ich używać zamiennie, opierając się w razie potrzeby na właściwościach kontinuum lub kombinatorycznych i można je rozszerzyć do n wymiarów. Kluczową właściwością ułatwiającą tę spójność jest to, że klasa zamkniętych podzbiorów regularnych ℝ n pokrywa się dokładnie z jednorodnie n -wymiarowymi wielościanami topologicznymi. Dlatego każdą n -wymiarową bryłę można jednoznacznie przedstawić przez jej granicę, a granica ma kombinatoryczną strukturę n-1 -wymiarowy wielościan posiadający jednorodnie n-1 -wymiarowe sąsiedztwa.
Solidne schematy reprezentacji
W oparciu o przyjęte właściwości matematyczne dowolny schemat reprezentacji brył jest metodą uchwycenia informacji o klasie półanalitycznych podzbiorów przestrzeni euklidesowej. Oznacza to, że wszystkie reprezentacje to różne sposoby organizowania tych samych danych geometrycznych i topologicznych w formie struktury danych . Wszystkie schematy reprezentacji są zorganizowane w kategoriach skończonej liczby operacji na zbiorze prymitywów. Dlatego przestrzeń modelowania dowolnej konkretnej reprezentacji jest skończona, a dowolny pojedynczy schemat reprezentacji może nie wystarczyć całkowicie do reprezentowania wszystkich typów brył. Na przykład bryły zdefiniowane za pomocą kombinacje uregulowanych operacji boolowskich nie muszą być koniecznie reprezentowane jako przeciągnięcie prymitywu poruszającego się po trajektorii przestrzennej, z wyjątkiem bardzo prostych przypadków. Zmusza to współczesne systemy modelowania geometrycznego do utrzymywania kilku schematów reprezentacji brył, a także ułatwia efektywną konwersję pomiędzy schematami reprezentacji.
Poniżej znajduje się lista typowych technik używanych do tworzenia lub przedstawiania modeli bryłowych. Nowoczesne oprogramowanie do modelowania może wykorzystywać kombinację tych schematów do przedstawienia bryły.
Instancja prymitywna
Schemat ten opiera się na koncepcji rodzin obiektów, przy czym każdy członek rodziny różni się od drugiego kilkoma parametrami. Każda rodzina obiektów nazywana jest ogólnym prymitywem , a poszczególne obiekty w rodzinie nazywane są instancjami prymitywnymi . Na przykład rodzina śrub jest ogólnym prymitywem, a pojedyncza śruba określona przez określony zestaw parametrów jest instancją prymitywu. Cechą wyróżniającą czysto sparametryzowane schematy instancji jest brak środków umożliwiających łączenie instancji w celu tworzenia nowych struktur reprezentujących nowe i bardziej złożone obiekty. Inną główną wadą tego schematu jest trudność pisania algorytmy obliczania właściwości reprezentowanych brył. W algorytmy musi być wbudowana znaczna ilość informacji specyficznych dla rodziny, dlatego też każdy rodzajowy element pierwotny należy traktować jako szczególny przypadek, co nie pozwala na jednolite ogólne traktowanie.
Wyliczenie obłożenia przestrzennego
Schemat ten jest zasadniczo listą komórek przestrzennych zajmowanych przez bryłę. Komórki, zwane także wokselami , są sześcianami o ustalonym rozmiarze i ułożonymi w stałą siatkę przestrzenną (możliwe są również inne układy wielościenne, ale sześciany są najprostsze). Każda komórka może być reprezentowana przez współrzędne pojedynczego punktu, np. środka ciężkości komórki. Zwykle narzucana jest określona kolejność skanowania, a odpowiadający jej uporządkowany zestaw współrzędnych nazywany jest tablicą przestrzenną . Tablice przestrzenne są jednoznacznymi i unikalnymi reprezentacjami stałymi, ale są zbyt szczegółowe, aby można je było używać jako reprezentacje „główne” lub definicyjne. Mogą jednak stanowić przybliżone przybliżenia części i można je wykorzystać do poprawy wydajności algorytmów geometrycznych, szczególnie w połączeniu z innymi reprezentacjami, takimi jak konstrukcyjna geometria bryłowa .
Rozkład komórek
Schemat ten wynika z kombinatorycznych (topologicznych) opisów brył wyszczególnionych powyżej. Ciało stałe można przedstawić poprzez jego rozkład na kilka komórek. Schematy wyliczenia obłożenia przestrzennego są szczególnym przypadkiem rozkładu komórek, w którym wszystkie komórki są sześcienne i układają się w regularną siatkę. Rozkłady komórek zapewniają wygodne sposoby obliczania pewnych właściwości topologicznych brył, takich jak ich łączność (liczba części) i rodzaj (liczba otworów). Rozkłady komórek w formie triangulacji są reprezentacjami stosowanymi w trójwymiarowych elementach skończonych do numerycznego rozwiązywania równań różniczkowych cząstkowych. Inne rozkłady komórek, takie jak regularne rozwarstwienie Whitneya lub rozkłady Morse'a, mogą być stosowane w zastosowaniach w planowaniu ruchu robota.
Modelowanie siatki powierzchniowej
Podobnie jak w przypadku reprezentacji granic, reprezentowana jest powierzchnia obiektu. Jednak zamiast skomplikowanych struktur danych i NURBS używana jest prosta siatka powierzchniowa wierzchołków i krawędzi. Siatki powierzchniowe mogą mieć strukturę (jak siatki trójkątne w plikach STL lub siatki kwadratowe z poziomymi i pionowymi pierścieniami czworoboków) lub siatki nieustrukturyzowane z losowo pogrupowanymi trójkątami i wielokątami wyższego poziomu.
Konstruktywna geometria bryłowa
Konstruktywna geometria brył (CSG) to rodzina schematów przedstawiania brył sztywnych jako konstrukcji boolowskich lub kombinacji prymitywów za pomocą omówionych powyżej operacji na zbiorach uregulowanych. CSG i reprezentacje brzegowe są obecnie najważniejszymi schematami reprezentacji brył. Reprezentacje CSG mają postać uporządkowanych drzew binarnych , gdzie węzły niekońcowe reprezentują albo sztywne transformacje ( izometrie zachowujące orientację ), albo uregulowane operacje na zbiorach. Węzły końcowe to prymitywne liście, które reprezentują zamknięte zbiory regularne. Semantyka reprezentacji CSG jest jasna. Każde poddrzewo reprezentuje zbiór wynikający z zastosowania wskazanych przekształceń/uregulowanych operacji na zbiorach na zbiorze reprezentowanym przez prymitywne liście poddrzewa. Reprezentacje CSG są szczególnie przydatne do uchwycenia założeń projektowych w postaci cech odpowiadających dodaniu lub usunięciu materiału (wypustki, otwory, kieszenie itp.). Atrakcyjne właściwości CSG obejmują zwięzłość, gwarantowaną ważność brył, wygodne obliczeniowo właściwości algebraiczne Boole'a i naturalną kontrolę kształtu bryły w kategoriach parametrów wysokiego poziomu definiujących prymitywy bryły oraz ich położenie i orientację. Stosunkowo prosta struktura danych i elegancka rekurencyjne dodatkowo przyczyniły się do popularności CSG.
Zamaszysty
Podstawowe pojęcie zawarte w szeroko zakrojonych schematach jest proste. Zbiór poruszający się w przestrzeni może śledzić lub wymiatać objętość (bryłę), która może być reprezentowana przez poruszający się zbiór i jego trajektorię. Taka reprezentacja jest istotna w kontekście zastosowań takich jak wykrywanie materiału usuwanego z frezu podczas jego przemieszczania się po określonej trajektorii, obliczania dynamicznej interferencji dwóch brył znajdujących się w ruchu względnym, planowania ruchu, a nawet w zastosowaniach grafiki komputerowej, takich jak śledzenie ruchu ruchy pędzla przesuwanego po płótnie. Większość komercyjnych systemów CAD zapewnia (ograniczoną) funkcjonalność konstruowania brył ukośnych, głównie w postaci dwuwymiarowego przekroju poprzecznego poruszającego się po trajektorii przestrzennej poprzecznej do przekroju. Jednakże obecne badania wykazały kilka przybliżeń trójwymiarowych kształtów poruszających się w ramach jednego parametru, a nawet ruchów wieloparametrowych.
Ukryta reprezentacja
Bardzo ogólną metodą definiowania zbioru punktów X jest określenie predykatu , który można ocenić w dowolnym punkcie przestrzeni. Innymi słowy, X definiuje się domyślnie jako składające się ze wszystkich punktów spełniających warunek określony przez predykat. Najprostszą formą predykatu jest warunek na znaku funkcji o wartościach rzeczywistych, co skutkuje znaną reprezentacją zbiorów za pomocą równości i nierówności. Na przykład, jeśli warunki , i reprezentują odpowiednio płaszczyznę i dwie otwarte liniowe półprzestrzenie . Bardziej złożone prymitywy funkcjonalne można zdefiniować za pomocą kombinacji logicznych prostszych predykatów. Ponadto teoria funkcji R pozwalają na konwersję takich reprezentacji na nierówność pojedynczej funkcji dla dowolnego zamkniętego zbioru półanalitycznego. Taką reprezentację można przekształcić w reprezentację graniczną za pomocą algorytmów poligonizacji, na przykład maszerujących kostek .
Modelowanie parametryczne i oparte na cechach
Funkcje definiuje się jako kształty parametryczne powiązane z atrybutami , takimi jak wewnętrzne parametry geometryczne (długość, szerokość, głębokość itp.), położenie i orientacja, tolerancje geometryczne , właściwości materiału i odniesienia do innych cech. Funkcje zapewniają także dostęp do powiązanych procesów produkcyjnych i modeli zasobów. Zatem cechy mają wyższy poziom semantyczny niż prymitywne zamknięte zbiory regularne. Ogólnie oczekuje się, że funkcje będą stanowić podstawę do łączenia CAD z dalszymi aplikacjami produkcyjnymi, a także do organizowania baz danych do ponownego wykorzystania danych projektowych. Modelowanie parametryczne oparte na cechach jest często łączone z konstrukcyjną geometrią brył binarnych (CSG), aby w pełni opisać systemy złożonych obiektów w inżynierii.
Historia solidnych modelarzy
Historyczny rozwój twórców modeli bryłowych należy postrzegać w kontekście całej historii CAD , a kluczowymi kamieniami milowymi był rozwój systemu badawczego BUILD, a następnie jego komercyjny spin-off Romulus , który wpłynął na rozwój Parasolid , ACIS i Rozwiązania w zakresie modelowania bryłowego . Jeden z pierwszych programistów CAD we Wspólnocie Niepodległych Państw (CIS), firma ASCON rozpoczęła w latach 90. wewnętrzny rozwój własnego narzędzia do modelowania brył. W listopadzie 2012 roku oddział matematyczny ASCON stał się odrębną firmą i otrzymał nazwę C3D Labs . Przydzielono mu zadanie opracowania jądra do modelowania geometrycznego C3D jako samodzielnego produktu – jedynego komercyjnego jądra do modelowania 3D z Rosji. Inny wkład wniósł Mäntylä ze swoim GWB oraz projekt GPM, który na początku lat 80. XX wieku wniósł między innymi wkład w techniki modelowania hybrydowego. Dzieje się tak również w przypadku języka programowania Solid Modeling PLaSM powstał na uniwersytecie w Rzymie.
Projektowanie wspomagane komputerowo
Modelowanie brył to jedynie minimum możliwości systemu CAD . W ciągu ostatnich dziesięciu lat osoby zajmujące się modelowaniem brył stały się powszechne na wydziałach inżynieryjnych [ kiedy? ] ze względu na szybsze komputery i konkurencyjne ceny oprogramowania. Oprogramowanie do modelowania bryłowego tworzy wirtualną reprezentację 3D komponentów na potrzeby projektowania i analizy maszyn. Typowy graficzny interfejs użytkownika zawiera programowalne makra, skróty klawiaturowe i dynamiczną manipulację modelem. Podkreślona jest możliwość dynamicznej reorientacji modelu w cieniowanym trójwymiarowym środowisku w czasie rzeczywistym, co pomaga projektantowi zachować mentalny obraz 3D.
Model części bryłowej zazwyczaj składa się z grupy elementów, dodawanych pojedynczo, aż do ukończenia modelu. Inżynierskie modele bryłowe są budowane głównie przy użyciu funkcji opartych na szkicowniku; Szkice 2D, które są przesuwane wzdłuż ścieżki, aby stać się trójwymiarowymi. Mogą to być na przykład wycięcia lub wytłoczki. Prace projektowe nad komponentami są zwykle wykonywane w kontekście całego produktu przy użyciu modelowania złożeń . Model złożenia zawiera odniesienia do poszczególnych modeli części składających się na produkt.
Innym rodzajem techniki modelowania jest „napawanie” ( modelowanie powierzchni swobodnych ). W tym przypadku powierzchnie są definiowane, przycinane, łączone i wypełniane w celu uzyskania bryły. Powierzchnie są zwykle definiowane za pomocą krzywych odniesienia w przestrzeni i różnych złożonych poleceń. Napawanie jest trudniejsze, ale lepiej nadaje się do niektórych technik produkcyjnych, takich jak formowanie wtryskowe. Modele bryłowe części formowanych wtryskowo zwykle mają zarówno funkcje oparte na powierzchni, jak i szkicowniku.
Rysunki techniczne można tworzyć półautomatycznie i odwoływać się do modeli bryłowych.
Modelowanie parametryczne
Modelowanie parametryczne wykorzystuje parametry do zdefiniowania modelu (na przykład wymiary). Przykładami parametrów są: wymiary używane do tworzenia elementów modelu, gęstość materiału, formuły opisujące elementy przeciągnięcia, importowane dane (na przykład opisujące powierzchnię odniesienia). Parametr można zmodyfikować później, a model zostanie zaktualizowany w celu odzwierciedlenia modyfikacji. Zazwyczaj istnieje związek pomiędzy częściami, zespołami i rysunkami. Część składa się z wielu elementów, a złożenie składa się z wielu części. Rysunki mogą być wykonane z części lub złożeń.
Przykład: Wałek jest tworzony przez wyciągnięcie okręgu o średnicy 100 mm. Na końcu wału zamontowana jest piasta. Później wał jest modyfikowany tak, aby miał długość 200 mm (kliknij na wał, wybierz wymiar długości, zmodyfikuj na 200). Po aktualizacji modelu wał będzie miał długość 200 mm, piasta przesunie się na koniec wału, do którego została zamontowana, a rysunki techniczne i właściwości masy automatycznie odzwierciedlą wszystkie zmiany.
Powiązane z parametrami, ale nieco inne, są ograniczenia . Więzy to relacje pomiędzy elementami tworzącymi określony kształt. W przypadku okna boki można zdefiniować jako równoległe i o tej samej długości. Modelowanie parametryczne jest oczywiste i intuicyjne. Jednak przez pierwsze trzy dekady CAD tak nie było. Modyfikacja oznaczała ponowne narysowanie lub dodanie nowego wycięcia lub występu na starych. Wymiary na rysunkach technicznych zostały utworzone , a nie pokazane . Modelowanie parametryczne ma ogromne możliwości, ale wymaga większych umiejętności w tworzeniu modelu. Skomplikowany model dla formowana wtryskowo może mieć tysiąc cech, a modyfikacja wczesnej cechy może spowodować awarię późniejszych funkcji. Umiejętnie utworzone modele parametryczne są łatwiejsze w utrzymaniu i modyfikacji. Modelowanie parametryczne nadaje się również do ponownego wykorzystania danych. W jednym modelu można na przykład zawrzeć całą rodzinę śrub z łbem walcowym .
Modelowanie brył medycznych
Nowoczesne skanery tomografii komputerowej i rezonansu magnetycznego można wykorzystać do tworzenia solidnych modeli cech wewnętrznych ciała, zwanych modelami opartymi na wokselach , z obrazami generowanymi za pomocą renderowania objętościowego . Optyczne skanery 3D można wykorzystać do tworzenia chmur punktów lub modeli siatek wielokątnych zewnętrznych cech ciała.
Zastosowania medycznego modelowania bryłowego;
- Wyobrażanie sobie
- Wizualizacja określonych tkanek ciała (na przykład naczyń krwionośnych i guza)
- Projektowanie protez , ortez i innych wyrobów medycznych i dentystycznych (czasami nazywa się to masową personalizacją )
- Tworzenie modeli siatek wielokątnych do szybkiego prototypowania (np. w celu pomocy chirurgom przygotowującym się do trudnych operacji)
- Łączenie modeli siatki wielokątnej z modelowaniem bryłowym CAD (na przykład projektowanie części zamiennych stawu biodrowego)
- Analiza obliczeniowa złożonych procesów biologicznych, np. przepływu powietrza, przepływu krwi
- Symulacja obliczeniowa nowych wyrobów medycznych i implantów in vivo
Jeśli zastosowanie wykracza poza wizualizację danych skanowania, konieczne będą procesy takie jak segmentacja obrazu i tworzenie siatki opartej na obrazach, aby wygenerować dokładny i realistyczny opis geometryczny danych skanowania.
Inżynieria
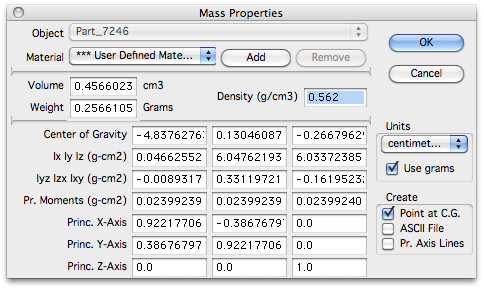
Ponieważ programy CAD działające na komputerach „rozumieją” prawdziwą geometrię obejmującą złożone kształty, można szybko obliczyć wiele atrybutów bryły 3-D, takich jak jej środek ciężkości, objętość i masa. Na przykład sześcian z zaokrąglonymi krawędziami pokazany na górze tego artykułu ma wymiary 8,4 mm od płaskiej do płaskiej. Pomimo wielu promieni i płytkiej piramidy na każdej z sześciu ścian, projektant może łatwo obliczyć jego właściwości, jak pokazano na zrzucie ekranu po prawej stronie.
Zobacz też
- Geometria obliczeniowa
- Grafika komputerowa
- Rysunek techniczny
- Reprezentacja granicy Eulera
- Lista firm CAx
- PLaSM – język programowania modelowania bryłowego.
- Rysunek techniczny