Twierdzenie trzech geodezów
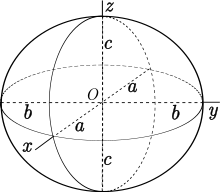
W geometrii różniczkowej twierdzenie o trzech geodezjach , znane również jako twierdzenie Lyusternika-Schnirelmanna , stwierdza, że każda rozmaitość Riemanna o topologii kuli ma co najmniej trzy geodezje proste domknięte (tj. trzy osadzone okręgi geodezyjne). Wynik można również rozszerzyć na quasi-geodezję na wypukłym wielościanie i na geodezję zamkniętą odwracalnego Finslera 2-kulki. Twierdzenie jest ostre: chociaż każda Riemanna 2-sfera zawiera nieskończenie wiele różnych zamkniętych geodezyjnych, tylko trzy z nich gwarantują brak samoprzecięć. Na przykład, w wyniku Morse'a , jeśli długości trzech głównych osi elipsoidy są różne, ale wystarczająco blisko siebie, to elipsoida ma tylko trzy proste geodezyjne zamknięte.
Historia i dowód
Geodezyjna , na powierzchni Riemanna, jest krzywą, która jest lokalnie prosta w każdym ze swoich punktów . Na przykład na płaszczyźnie euklidesowej geodezyjnymi są linie , a na powierzchni kuli geodezyjnymi są koła wielkie . Najkrótsza ścieżka na powierzchni między dwoma punktami jest zawsze geodezyjna, ale mogą istnieć również inne geodezyjne. Mówi się, że geodezja jest geodezyjną zamkniętą , jeśli powraca do swojego punktu początkowego i kierunku początkowego; w ten sposób może krzyżować się wiele razy. Twierdzenie trzech geodezyjnych mówi, że dla powierzchni homeomorficznych kuli, istnieją co najmniej trzy nieprzekraczające się geodezyjne zamknięte. Może ich być więcej niż trzy, na przykład sama kula ma nieskończenie wiele.
Wynik ten wynika z matematyki nawigacji oceanicznej, gdzie powierzchnię ziemi można dokładnie modelować za pomocą elipsoidy , oraz z badań geodezyjnych na elipsoidzie , najkrótszej ścieżce pokonywanej przez statki. W szczególności prawie kulista trójosiowa elipsoida ma tylko trzy proste geodezyjne zamknięte, jej równiki. W 1905 roku Henri Poincaré przypuszczał, że każda gładka powierzchnia topologicznie równoważna kuli również zawiera co najmniej trzy proste geodezyjne zamknięte, aw 1929 roku Lazar Lyusternik i Lev Schnirelmann opublikował dowód przypuszczenia; chociaż ogólny topologiczny argument dowodu był poprawny, wykorzystał wynik deformacji, który później okazał się błędny. Kilku autorów zaproponowało niezadowalające rozwiązania luki. Powszechnie akceptowane rozwiązanie zaproponował w latach 80. XX wieku Grayson za pomocą przepływu skracającego krzywą
Uogólnienia
Wzmocniona wersja twierdzenia stwierdza, że na dowolnej powierzchni Riemanna, która jest topologicznie kulą, koniecznie istnieją trzy proste geodezyjne domknięte, których długość jest co najwyżej proporcjonalna do średnicy powierzchni.
Liczba geodezji zamkniętych o długości co najwyżej L na gładkiej kuli topologicznej rośnie proporcjonalnie do L / log L , ale nie można zagwarantować, że wszystkie takie geodezje będą proste.
Na zwartych hiperbolicznych powierzchniach Riemanna istnieje nieskończenie wiele prostych geodezji zamkniętych, ale tylko skończenie wiele z określoną długością. Są one kodowane analitycznie przez funkcję zeta Selberga . Tempo wzrostu liczby geodezji prostych zamkniętych w funkcji ich długości badała Maryam Mirzakhani .
Istnienie trzech prostych zamkniętych geodezyjnych dotyczy również dowolnej odwracalnej metryki Finslera na 2-sferze.
Niepłynne metryki
Czy istnieje algorytm, który może znaleźć prostą zamkniętą quasi-geodezę na wypukłym wielościanie w czasie wielomianowym?
Możliwe jest również zdefiniowanie geodezji na niektórych powierzchniach, które nie wszędzie są gładkie, takich jak wielościany wypukłe . Powierzchnia wypukłego wielościanu ma metrykę, która jest lokalnie euklidesowa, z wyjątkiem wierzchołków wielościanu, a krzywa, która omija wierzchołki, jest geodezyjna, jeśli przebiega wzdłuż odcinków linii prostych w obrębie każdej ściany wielościanu i pozostaje prosta w poprzek każdej krawędzi wielościanu że się przecina. Chociaż niektóre wielościany mają proste zamknięte geodezje (na przykład regularny czworościan i dwusfenoidy mają nieskończenie wiele zamkniętych geodezyjnych, wszystkie proste), inne nie. W szczególności prosta zamknięta geodezja wielościanu wypukłego musiałaby przeciąć całkowity defekt kątowy wierzchołków na pół, a prawie wszystkie wielościany nie mają takich dwusiecznych.
Niemniej jednak twierdzenie trzech geodezyjnych można rozszerzyć na wielościany wypukłe, biorąc pod uwagę quasi-geodezy, krzywe, które są geodezyjne z wyjątkiem wierzchołków wielościanów i które mają kąty mniejsze niż π po obu stronach w każdym wierzchołku, przez który przecinają . Wersja twierdzenia o trzech geodezjach dla wypukłych wielościanów stwierdza, że wszystkie wielościany mają co najmniej trzy proste zamknięte quasi-geodezy; można to udowodnić, przybliżając wielościan gładką powierzchnią i stosując twierdzenie trzech geodezyjnych do tej powierzchni. Otwartym problemem jest to , czy którąkolwiek z tych quasi-geodezyjnych można zbudować czas wielomianowy .