Antymatroid

Trzy widoki antymatroidu: inkluzja porządkująca w swojej rodzinie dopuszczalnych zbiorów, język formalny i odpowiadający mu zestaw ścieżek.

W matematyce antymatroid to formalny system opisujący procesy, w których zestaw jest tworzony przez włączanie elementów pojedynczo, i w którym element raz dostępny do włączenia pozostaje dostępny, dopóki nie zostanie uwzględniony. Antymatroidy są zwykle aksjomatyzowane na dwa równoważne sposoby , albo jako zestaw systemów modelujących możliwe stany takiego procesu, albo jako formalny język modelujący różne sekwencje, w których elementy mogą być zawarte. Dilwortha (1940) był pierwszym, który badał antymatroidy, stosując kolejną aksjomatyzację opartą na teorii sieci i często były one ponownie odkrywane w innych kontekstach.

Aksjomaty definiujące antymatroidy jako systemy zestawów są bardzo podobne do aksjomatów matroidów , ale podczas gdy matroidy są definiowane przez aksjomat wymiany , antymatroidy są definiowane zamiast tego przez aksjomat antywymiany , od którego wywodzi się ich nazwa. Antymatroidy można postrzegać jako szczególny przypadek greedoidów i sieci semimodularnych oraz jako uogólnienie rzędów częściowych i sieci dystrybucyjnych . Antymatroidy są równoważne, poprzez dopełnienie , wypukłym geometriom , kombinatoryczna abstrakcja zbiorów wypukłych w geometrii .

Antymatroidy zostały zastosowane do modelowania ograniczeń pierwszeństwa w problemach z planowaniem , potencjalnych sekwencji zdarzeń w symulacjach, planowania zadań w sztucznej inteligencji oraz stanów wiedzy uczniów.

Definicje

Antymatroid można zdefiniować jako skończoną rodzinę skończonych zbiorów, zwanych zestawami wykonalnymi , o następujących dwóch właściwościach: ${\ displaystyle {\ mathcal {F}}}$

• Połączenie dowolnych dwóch możliwych zestawów jest również wykonalne . $Oznacza$ to, że zamknięty w związkach.
• Jeśli $Displaystyle$$x$ możliwym zbiorem, to zawiera element , dla którego $($ zestaw utworzony przez usunięcie z $}$$S \ setminus \ {x$$jest$ . $Oznacza$ to, że dostępnym systemem zbiorów .

Antymatroidy mają również równoważną definicję jako język formalny , to znaczy jako zestaw ciągów zdefiniowanych ze skończonego alfabetu symboli . Łańcuch należący do tego zbioru nazywany jest słowem języka. Język definiujący antymatroid musi spełniać następujące właściwości: ${\ displaystyle {\ mathcal {L}}}$

• Każdy symbol alfabetu występuje w co najmniej jednym słowie ${\ displaystyle {\ mathcal {L}}}$ .
• Każde słowo zawiera co $.$ jedną kopię każdego symbolu Język z tą właściwością jest nazywany normalnym .
• Każdy przedrostek słowa w ${\ displaystyle {\ mathcal {L}}}$ jest również w ${\ displaystyle {\ mathcal {L}}}$ . Język z tą właściwością nazywany jest dziedzicznym .
• Jeśli i ${\ displaystyle S}$$zawiera$ T $\ displaystyle T}$ są słowami w , a ${\ displaystyle S}$ co najmniej jeden symbol, którego nie ma w ${\ displaystyle S} T}$$\ displaystyle {\$$}$ jest symbol $}$ taki, że konkatenacja $jest$ innym słowem w mathcal {L .

Równoważność tych dwóch form definicji można zobaczyć w następujący sposób. Jeśli $język$ formalny, to zbiory symboli w słowach tworzą dostępny system zbiorów zamkniętych związkami $\ mathcal {L}}}$ . Jest dostępny dzięki dziedzicznej właściwości łańcuchów i można wykazać, że jest zamknięty przez sumę przez wielokrotne zastosowanie właściwości konkatenacji ciągów. W przeciwnym kierunku, z dostępnego systemu zbiorów zamkniętych związkami, język normalnych ciągów znaków, których wszystkie przedrostki mają zestawy symboli należących do ${\ displaystyle {\ mathcal {F}}}$ spełnia wymagania, aby język formalny był antymatroidem. ${\ displaystyle {\ mathcal {F}}}$ Te dwie transformacje są wzajemnymi odwrotnościami: przekształcenie języka formalnego w ustaloną rodzinę iz powrotem lub odwrotnie, daje ten sam system. Zatem te dwie definicje prowadzą do matematycznie równoważnych klas obiektów.

Przykłady

Sekwencja ostrzału płaskiego zestawu punktów. Segmenty linii przedstawiają krawędzie otoczek wypukłych po usunięciu niektórych punktów.

Następujące systemy dostarczają przykładów antymatroidów:

Antymatroidy łańcuchowe

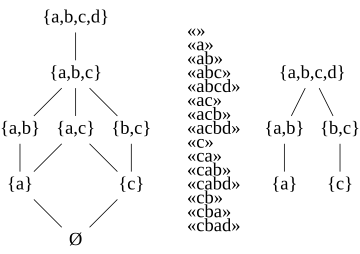
Przedrostki pojedynczego ciągu i zestawy symboli w tych przedrostkach tworzą antymatroid. Na przykład antymatroid łańcuchowy zdefiniowany przez łańcuch ma jako język formalny zbiór ciągów $\ displaystyle abcd}$

$${\ Displaystyle \ {\ varepsilon, a, ab, abc, abcd \}$$

(gdzie oznacza pusty ciąg ) i jako rodzina wykonalnych zestawów rodzina ${\ displaystyle \ varepsilon}$

$${\ Displaystyle {\ bigl \ {} \ pusty zbiór, \ {a \}, \ {a, b \}, \ {a, b, c \}, \ {a, b, c, d \} {\ bigr \}}.}$$

Posetowe antymatroidy

Niższe zbiory skończonego, częściowo uporządkowanego zbioru tworzą antymatroid, przy czym pełne słowa antymatroidu tworzą liniowe przedłużenia częściowego porządku. Zgodnie z twierdzeniem Birkhoffa o reprezentacji dla sieci rozdzielczych, możliwe zbiory w antymatroidzie poset (uporządkowane przez inkluzje zbioru) tworzą siatkę rozdzielczą, a wszystkie sieci rozdzielcze można utworzyć w ten sposób. Zatem antymatroidy można postrzegać jako uogólnienia sieci dystrybucyjnych. Antymatroid łańcuchowy jest szczególnym przypadkiem antymatroidu poset dla całkowitego porządku .

antymatroidów

Łuskanie Sekwencja ostrzału skończonego zbioru $jest$ na płaszczyźnie euklidesowej lub wielowymiarowej przestrzeni euklidesowej tworzona przez wielokrotne usuwanie wierzchołków wypukłej otoczki . Możliwymi zestawami antymatroidów utworzonych przez te sekwencje są przecięcia z dopełnieniem U { \ $U}$ zbioru wypukłego. Każdy antymatroid jest izomorficzny z łuskającym antymatroidem punktów w wystarczająco wielowymiarowej przestrzeni.

Doskonała eliminacja

Doskonałe uporządkowanie eliminacji grafu akordowego to uporządkowanie jego wierzchołków w taki sposób, że dla każdego wierzchołka $}$$grafów$ akordowych występujący później niż $displaystyle v$ zamawianie z kliki . Przedrostki doskonałych porządków eliminacji wykresu akordowego tworzą antymatroid.

Gry z odpalaniem wiórów

Gry z odpalaniem wiórów, takie jak abelowy model piaskowca, są definiowane przez graf skierowany wraz z systemem „żetonów” umieszczonych na jego wierzchołkach. Ilekroć liczba żetonów na wierzchołku $z$$nich$ najmniej tak duża, jak liczba krawędzi z $.$ możliwe jest wystrzelenie , przesuwając jeden żeton do każdego sąsiedni wierzchołek. Zdarzenie, które uruchamia się dla ${\ displaystyle v}$$tylko wtedy$$displaystyle i} ten$$się$ wystrzelił zgromadził liczbę Warunki te nie zależą od kolejności poprzednich odpaleń i pozostają prawdziwe do momentu $,$ więc każdy dany wykres i początkowe rozmieszczenie żetonów, dla których system się kończy, definiuje antymatroid na parach ${\ Displaystyle (v, i)}$ . Konsekwencją właściwości antymatroidów tych systemów jest to, że dla danego stanu początkowego liczba odpaleń każdego wierzchołka i ostateczny stabilny stan systemu nie zależą od kolejności odpalania.

Ścieżki i podstawowe słowa

W teorii mnogościowej aksjomatyzacji antymatroidu istnieją pewne specjalne zbiory zwane ścieżkami , które określają całą antymatroidę w tym sensie, że zbiory antymatroidu są dokładnie sumami ścieżek. Jeśli $,$ dowolnym możliwym zbiorem antymatroidu, element , który można usunąć z, aby utworzyć $, a możliwy zestaw, który$ nazywany jest punktem końcowym $\ displaystyle$ końcowy , nazywa się $S}$ ścieżka antymatroidu. Rodzinę ścieżek można częściowo uporządkować przez włączenie zestawu, tworząc zestaw ścieżek antymatroidu.

Dla każdego wykonalnego zestawu w antymatroidzie i każdego elementu $można$ S $}$$displaystyle S$ znaleźć podzbiór ścieżki z ${\ displaystyle S}$ , dla którego $x}$${\ displaystyle$ jest punktem końcowym: aby to zrobić, usuwaj pojedynczo elementy inne niż ${\ displaystyle x}$ , aż żadne takie usunięcie nie pozostawi wykonalnego podzbioru. Dlatego każdy możliwy zestaw w antymatroidzie jest sumą jego podzbiorów ścieżek. jeśli ${\ Displaystyle S}$ nie jest ścieżką, każdy podzbiór w tej unii jest właściwym podzbiorem S $\ displaystyle S}$ . Ale jeśli $x}$ ścieżką z punktem końcowym $każdy$ właściwy podzbiór należący do antymatroidu wyklucza $S$${$ . Dlatego ścieżki antymatroidu są dokładnie możliwymi zbiorami, które nie są równe związkom ich właściwych wykonalnych podzbiorów. Równoważnie, dana rodzina zbiorów ${\ Displaystyle {\ mathcal {P}}}$ tworzy rodzinę ścieżek antymatroidu wtedy i tylko wtedy, gdy dla każdego sumy podzbiorów ${\ displaystyle S}$ w ${\ displaystyle {\ mathcal {P}}}$ z ${\ displaystyle S}$$w$ ma o jeden element $niż$ . Jeśli tak, $jest$ rodziną związków podzbiorów $}}$ .

W formalizacji języka formalnego antymatroidu najdłuższe ciągi nazywane są słowami podstawowymi . Każde podstawowe słowo tworzy permutację całego alfabetu. Jeśli jest zbiorem podstawowych słów, można zdefiniować z $jako$$B}$$Displaystyle$ zbiór przedrostków słów w $\ displaystyle B}$ .

Geometria wypukła

Zobacz też: zbiór wypukły , geometria wypukła i operator domknięcia

Jeśli jest zbiorczym systemem definiującym antymatroid, z równym sumie zbiorów w , to $fa$$\$$displaystyle {\ mathcal {F$ } rodzina zestawów

$${\ Displaystyle {\ mathcal {G}} = \ {U \ setminus S \ mid S \ w {\ mathcal {F}} \}}$$

komplementarne $czasami$ zbiorów w $,$ nazywane geometrią wypukłą a zbiory w są nazywane zestawami wypukłymi . Na przykład w łuskającym antymatroidzie zbiory wypukłe są przecięciami danego zbioru punktów z wypukłymi podzbiorami przestrzeni euklidesowej. Układ zbioru definiujący geometrię wypukłą musi być domknięty pod przecięciami. Dla dowolnego zestawu w ${\ displaystyle$${\ mathcal {G}}},$ który nie jest równy S {\ displaystyle S ${\ displaystyle U}$ musi istnieć element, którego nie ma w $S}$$displaystyle$ , który można dodać do ${\ displaystyle S}$ , aby utworzyć inny zestaw w $displaystyle {\ mathcal {G} }}}$ .

Geometrię wypukłą można również zdefiniować za pomocą operatora $, który odwzorowuje$$.$ podzbiór z jego minimalnym zamkniętym nadzbiorem Aby być operatorem zamknięcia, powinien mieć następujące właściwości: ${\ displaystyle \ tau}$

• ${\ Displaystyle \ tau (\ pusty zbiór) = \ pusty zbiór$ : zamknięcie zbioru pustego jest puste.
• Dla każdego podzbioru ${\ Displaystyle \ tau (S)}$ U $,$$\ Displaystyle U}$ S $\ Displaystyle S}$ jest podzbiorem i ${\ Displaystyle \ tau (S) = \ tau {\ bigl (} \ tau (S) {\ bigr)}}$ .
• Ilekroć jest podzbiorem ${\ Displaystyle S \ podzbiór T \ podzbiór U}$ , ${\ Displaystyle \ tau (S)}$ jest podzbiorem ${\ Displaystyle \ tau (T)}$ .

Rodzina zbiorów zamkniętych wynikająca z operacji domknięcia tego typu jest z konieczności domknięta na przecięciach, ale może nie być geometrią wypukłą. Operatory domknięcia, które definiują geometrie wypukłe, spełniają również dodatkowy aksjomat przeciwwymienny :

• Jeśli jest podzbiorem $U$$,$${\ Displaystyle \ tau (S)}$$}$ i i są odrębnymi elementami ${\ displaystyle U}$ nie należą $($ , ale $Displaystyle$ do $\ tau (S \ kubek \ {y \})}$ , wtedy $($ należy do ${\ Displaystyle \ tau (S \ kubek \ {z \})$ .

Operacja domknięcia spełniająca ten aksjomat nazywana jest domknięciem przeciwwymiennym . Jeśli $} leq y}$ domknięciu przeciwwymiennym, to aksjomat przeciwwymienny określa częściowy porządek elementów nie należących do ${\ displaystyle S}$ , gdzie $S$ w częściowym porządku, gdy należy do $($${\ Displaystyle \ tau (S \ puchar \ {y \}$ . Jeśli $porządku$$elementem$ tego , Oznacza to, że rodzina zbiorów domkniętych domknięcia przeciwwymiennego ma tę właściwość, że dla każdego zbioru innego niż zbiór uniwersalny istnieje element ${\ displaystyle x}$ które można do niego dodać, aby utworzyć kolejny zbiór domknięty. Ta właściwość jest komplementarna z właściwością dostępności antymatroidów, a fakt, że przecięcia zbiorów domkniętych są domknięte, jest komplementarny z właściwością, że sumy dopuszczalnych zbiorów w antymatroidzie są wykonalne. Dlatego dopełnienia zbiorów zamkniętych dowolnego domknięcia przeciwwymiennego tworzą antymatroid.

Grafy nieskierowane , w których zbiory wypukłe (podzbiory wierzchołków zawierające wszystkie najkrótsze ścieżki między wierzchołkami w podzbiorze) tworzą geometrię wypukłą, to właśnie grafy ptolemejskie .

Siatki rozdzielcze

Każde dwa możliwe zestawy antymatroidu mają unikalną najmniejszą granicę górną (ich sumę) i unikalną największą granicę dolną (sumę zestawów w antymatroidzie, które są zawarte w obu z nich). Dlatego możliwe zbiory antymatroidu, częściowo uporządkowane przez inkluzje zbioru, tworzą siatkę . Różne ważne cechy antymatroidu można interpretować w kategoriach teorii sieci; na przykład ścieżki antymatroidu są nieredukowalnymi elementami odpowiedniej sieci, a podstawowe słowa antymatroidu odpowiadają maksymalne łańcuchy w sieci. Sieci powstające z antymatroidów w ten sposób uogólniają skończone sieci rozdzielcze i można je scharakteryzować na kilka różnych sposobów.

• Opis pierwotnie rozważany przez Dilwortha (1940) dotyczy nieredukowalnych elementów sieci. Dla $:$ elementu antymatroidu istnieje unikalny maksymalny możliwy zestaw, $x} }$ nie zawiera $}$$x$ : można skonstruować jako sumę wszystkich możliwych zestawów niezawierających ${\ displaystyle x}$ . Ten ${\ displaystyle S_ {x}}$ jest automatycznie nieredukowalny, co oznacza, że ​​nie jest to spotkanie dowolnych dwóch większych elementów sieci. $przecięcia$ to prawdą, ponieważ każdy możliwy nadzbiór $zawiera$ , a zatem możliwych nadzbiorów. Każdy element dowolnej sieci można rozłożyć na spotkanie zestawów nieredukowalnych, często na wiele sposobów, ale w sieci odpowiadającej antymatroidowi każdy element T {\ $T}$ ma unikalną minimalną rodzinę nieredukowalnych zestawów spotkań, których spotkaniem jest ${\ displaystyle T}$ ; $ta$$.$ ze zbiorów elementów takich $to$ Oznacza to, że sieć ma unikalne, nieredukowalne rozkłady .
• Druga charakterystyka dotyczy $x\równik z\równik y}$ w siatce, podkratach określonych przez parę elementów sieci składających $się$ ze wszystkich elementów sieci $}$$\ displaystyle$ . Interwał jest atomistyczny , jeśli każdy jego element jest połączeniem atomów (minimalne elementy powyżej dolnego elementu ) i jest logiczny ${\ displaystyle x}$ jeśli jest izomorficzny z kratą wszystkich podzbiorów skończonego zbioru. W przypadku antymatroidu każdy interwał, który jest atomistyczny, jest również logiczny.
• $y}$ , kraty powstające z antymatroidów to kraty semimodularne , kraty, $} displaystyle x \ klin y}$ spełniają górne prawo semimodularne , które dla każdych dwóch elementów i $Displaystyle$ obejmuje $\ displaystyle y$ { następnie ${\ displaystyle x \ vee y}$ obejmuje ${\ displaystyle x}$ . Przekładając ten warunek na możliwe zbiory antymatroidu, jeśli możliwy zestaw ma tylko jeden element nie należący do innego możliwego zestawu, to ten jeden element można dodać do X ${\ displaystyle$$}$$}$${\ displaystyle X$ , aby utworzyć kolejny zestaw w antymatroidzie. Dodatkowo krata antymatroidu ma $y}$ semidistributive : dla wszystkich elementów kraty , $displaystyle$ i ${\ displaystyle z}$${\ Displaystyle x \ klin y}$ i ${\ Displaystyle x \ klin z}$ są sobie równe, to również oba są równe x ${\ Displaystyle x \ klin (y \$ . Sieć semimodularna i semidystrybucyjna nazywana jest siecią dystrybucyjną łączącą .

Te trzy charakterystyki są równoważne: dowolna krata z unikalnymi rozkładami nieredukowalnymi ma boolowskie przedziały atomistyczne i jest rozdzielna z łączeniem, każda krata z boolowskimi przedziałami atomistycznymi ma unikalne rozkłady nieredukowalne i jest rozdzielna z łączeniem, a dowolna sieć rozdzielna z łączeniem ma unikalne spełniają nieredukowalne rozkłady i atomistyczne przedziały logiczne. Tak więc możemy odnosić się do kraty o dowolnej z tych trzech właściwości jako rozdzielczej łączenia. Każdy antymatroid daje początek skończonej sieci dystrybucyjnej łączącej, a każda skończona sieć dystrybucyjna łącząca pochodzi w ten sposób z antymatroidu. Inną równoważną charakterystyką skończonych sieci dystrybucyjnych łączących jest to, że tak jest stopniowane (dowolne dwa maksymalne łańcuchy mają tę samą długość), a długość maksymalnego łańcucha jest równa liczbie spotykanych nieredukowalnych elementów sieci. Antymatroid reprezentujący skończoną siatkę rozdzielającą łączenia można odzyskać z sieci: elementy antymatroidu można uznać za spotykane nieredukowalne elementy sieci, a możliwy zestaw odpowiadający dowolnemu elementowi x {\ $}$ x krata składa się z zestawu nieredukowalnych elementów, $}$ , że nie jest większa lub równa ${\ displaystyle y$${\ displaystyle x}$ w siatce.

Ta reprezentacja dowolnej skończonej sieci dystrybucyjnej łączącej jako dostępnej rodziny zbiorów zamkniętych na związki (to znaczy jako antymatroid) może być postrzegana jako analogia twierdzenia Birkhoffa o reprezentacji, zgodnie z którym każda skończona krata rozdzielcza ma reprezentację jako rodzina zbiorów zamknięte pod związkami i skrzyżowaniami.

Superrozpuszczalne antymatroidy

Zmotywowany problemem zdefiniowania rzędów częściowych na elementach grupy Coxetera , Armstrong (2009) badał antymatroidy, które są również sieciami superrozwiązywalnymi. Superrozwiązywalny antymatroid jest definiowany przez całkowicie uporządkowany zbiór elementów i rodzinę zbiorów tych elementów. Rodzina musi zawierać pusty zestaw. $\ displaystyle B}$ musi mieć tę właściwość, że jeśli dwa zbiory $i$ B należą do rodziny, to jeśli różnica teorii mnogości ${\ Displaystyle B \ setminus A}$ nie jest pusty, a jeśli jest najmniejszym elementem ${\ Displaystyle B \ setminus A}$$,$ ZA $\ Displaystyle A \ puchar \ {x\}}$ również należy do rodziny. Jak zauważa Armstrong, każda rodzina zbiorów tego typu tworzy antymatroid. Armstrong zapewnia również siatkową charakterystykę antymatroidów, które może tworzyć ta konstrukcja.

Połącz działanie i wymiar wypukły

Jeśli $antymatroid$$oba opisane jako rodzina$ zbiorów w tym samym wszechświecie elementów, to inny łączenie ZA ${\ displaystyle {\ mathcal {A}}}$ i można utworzyć w następujący sposób: ${\ displaystyle {\ mathcal {A}}$

$${\ Displaystyle {\ mathcal {A}} \ vee {\ mathcal {B}} = \ {S \ kubek T \ mid S \ in {\ mathcal {A}} \ klin T \ in {\ mathcal {B}} \}.}$$

Jest to inna operacja niż łączenie rozważane w charakterystykach antymatroidów opartych na teorii sieci: łączy dwa antymatroidy w celu utworzenia innego antymatroidu, zamiast łączenia dwóch zestawów w antymatroid w celu utworzenia innego zestawu. Rodzina wszystkich antymatroidów w tym samym wszechświecie tworzy półsieć dzięki tej operacji łączenia.

$displaystyle {\ mathcal {L}} }}$ , która odwzorowuje języki formalne na antymatroidy, gdzie zamknięcie języka jest przecięciem wszystkich antymatroidów zawierających ${\$ jako podjęzyk. To zamknięcie ma jako wykonalne zestawy związków przedrostków ciągów w ${\ displaystyle {\ mathcal {L}}}$ . Jeśli chodzi o tę operację zamknięcia, łączenie jest zamknięciem unii języków i B. ZA ${\ mathcal {A}}}$ \ mathcal ${B}}}$ Każdy antymatroid można przedstawić jako połączenie rodziny antymatroidów łańcuchowych lub równoważnie jako domknięcie zbioru podstawowych słów; wypukły wymiar antymatroidu to minimalna liczba antymatroidów łańcuchowych (lub równoważnie minimalna liczba podstawowych słów) w takiej $reprezentacji$ Jeśli jest rodziną łańcuchowych antymatroidów, których wszystkie podstawowe słowa należą do $fa$$displaystyle {\ mathfrak {F}}}$ { ${\ Displaystyle {\ mathfrak {F}}}$ generuje ${\ Displaystyle {\ mathcal {A}}}$ wtedy i tylko wtedy, gdy wykonalne zestawy z obejmują wszystkie ścieżki $}}$$\ displaystyle {\ mathcal {A}}}$$}$ . Ścieżki należące do antymatroidu jednołańcuchowego muszą tworzyć $łańcuch$ w pozycji ścieżki $\ mathcal {A}}}$ , więc wypukły wymiar antymatroidu jest równy minimalnej liczbie łańcuchów potrzebnych do pokrycia ścieżki, która zgodnie z twierdzeniem Dilwortha jest równa szerokości ścieżki.

Jeśli ktoś ma reprezentację antymatroidu jako domknięcie zestawu $podstawowych słów, wówczas$ reprezentacja może być użyta do odwzorowania możliwych zestawów antymatroidu na punkty w -wymiarowym euklidesie ${\ displaystyle d} przestrzeń: przypisz$${\ Displaystyle S}$ współrzędną do podstawowego słowa $i$ , aby wartość współrzędnej wykonalnego zestawu była długością najdłuższego przedrostka, który jest podzbiorem $W}$$displaystyle$ . Z tym osadzeniem, $jest$ podzbiorem innego możliwego zestawu $} styl wyświetlania T}$$i tylko wtedy, gdy$ współrzędne dla są mniejsze równe odpowiednim współrzędnym ${\ displaystyle S$ . Dlatego wymiar zamówienia uporządkowania inkluzji dopuszczalnych zbiorów jest co najwyżej równe wypukłemu wymiarowi antymatroidu. Jednak ogólnie te dwa wymiary mogą być bardzo różne: istnieją antymatroidy o trzecim wymiarze rzędu, ale z dowolnie dużym wymiarem wypukłym.

Wyliczenie

Liczba możliwych antymatroidów na zbiorze elementów rośnie szybko wraz z liczbą elementów w zbiorze. W przypadku zestawów składających się z jednego, dwóch, trzech itd. Elementów liczba różnych antymatroidów wynosi

$${\ Displaystyle 1,3,22,485,59386,133059751, \ kropki \,.}$$

Aplikacje

Zarówno pierwszeństwo, jak i ograniczenia czasowe zwolnienia w standardowej notacji dla teoretycznych problemów szeregowania mogą być modelowane przez antymatroidy. Boyd i Faigle (1990) używają antymatroidów do uogólnienia zachłannego algorytmu Eugene'a Lawlera do optymalnego rozwiązywania problemów z planowaniem jednoprocesorowym z ograniczeniami pierwszeństwa, w których celem jest zminimalizowanie maksymalnej kary ponoszonej przez spóźnione planowanie zadania.

Glasserman i Yao (1994) używają antymatroidów do modelowania kolejności zdarzeń w dyskretnych systemach symulacji zdarzeń.

Parmar (2003) wykorzystuje antymatroidy do modelowania postępów w realizacji celu w problemach planowania sztucznej inteligencji .

W teorii optymalności , matematycznym modelu rozwoju języka naturalnego opartym na optymalizacji w warunkach ograniczeń, gramatyki są logicznie równoważne antymatroidom.

W psychologii matematycznej antymatroidy były używane do opisywania możliwych stanów wiedzy ucznia. Każdy element antymatroidu reprezentuje pojęcie, które uczeń ma zrozumieć, lub klasę problemów, które może poprawnie rozwiązać, a zbiory elementów tworzące antymatroid reprezentują możliwe zestawy pojęć, które mogą być rozumiane przez jedną osobę. Aksjomaty definiujące antymatroid można sformułować nieformalnie jako stwierdzające, że uczenie się jednej koncepcji nigdy nie może uniemożliwić uczniowi nauczenia się innej koncepcji i że każdy możliwy stan wiedzy można osiągnąć, ucząc się pojedynczej koncepcji na raz. Zadaniem systemu oceny wiedzy jest wywnioskowanie zestawu pojęć znanych danemu uczącemu się poprzez analizę jego odpowiedzi na mały i dobrze dobrany zestaw problemów. W tym kontekście antymatroidy były również nazywane „przestrzeniami uczenia się” i „dobrze sklasyfikowanymi przestrzeniami wiedzy”.

Notatki

• Adariczewa, KV; Gorbunow, Wirginia; Tumanov, VI (2003), „Sieci półdystrybucyjne i geometrie wypukłe” , Advances in Mathematics , 173 (1): 1–49, doi : 10.1016 / S0001-8708 (02) 00011-7 .
•    , _ _ _ _ _ _ _ _ _ _ _ _ MR 2568800 , S2CID 15474840 .
•   Birkhoff, Garrett ; Bennett, MK (1985), „Krata wypukła poset” , Order , 2 (3): 223–242, doi : 10.1007 / BF00333128 , S2CID 118907732
•   Björner, Anders ; Lovász, László ; Shor, Peter W. (1991), „Gry z wypalaniem chipów na wykresach”, European Journal of Combinatorics , 12 (4): 283–291, doi : 10.1016 / S0195-6698 (13) 80111-4 , MR 1120415
•    Björner, Anders ; Ziegler, Günter M. (1992), „Wprowadzenie do greedoidów” , w White, Neil (red.), Matroid Applications , Encyclopedia of Mathematics and its Applications, tom. 40, Cambridge: Cambridge University Press, s. 284–357 , doi : 10.1017/CBO9780511662041.009 , ISBN 0-521-38165-7 , MR 1165537
• Boyd, E. Andrew; Faigle, Ulrich (1990), „Algorytmiczna charakterystyka antymatroidów”, Discrete Applied Mathematics , 28 (3): 197–205, doi : 10.1016/0166-218X (90) 90002-T , hdl : 1911/101636 .
• Chandran, LS; Ibarra, L.; Ruskey, F .; Sawada, J. (2003), „Generowanie i charakteryzacja doskonałych porządków eliminacji grafu akordowego” (PDF) , Theoretical Computer Science , 307 (2): 303–317, doi : 10.1016 / S0304-3975 (03) 00221- 4
•   Dilworth, Robert P. (1940), „Kraty z unikalnymi nieredukowalnymi rozkładami”, Annals of Mathematics , 41 (4): 771–777, doi : 10.2307/1968857 , JSTOR 1968857 .
•   Doignon, Jean-Paul; Falmagne, Jean-Claude (1999), Przestrzenie wiedzy , Springer-Verlag, ISBN 3-540-64501-2 .
•   . _ _ _ _ _ _ _ _ _ _ _
•   Edelman, Paweł H.; Saks, Michael E. (1988), „Kombinatoryczna reprezentacja i wypukły wymiar geometrii wypukłych” , Order , 5 (1): 23–32, doi : 10.1007 / BF00143895 , S2CID 119826035 .
• Eppstein, David (2008), Sekwencje uczenia się , arXiv : 0803.4030 . Częściowo zaadaptowane jako rozdziały 13 i 14   Falmagne, Jean-Claude ; Albert, Dietrich; Podwójne, Chris; Eppstein, David ; Hu, Xiangen, wyd. (2013), Przestrzenie wiedzy: zastosowania w edukacji , Springer-Verlag, doi : 10.1007/978-3-642-35329-1 , ISBN 978-3-642-35328-4 .
•   Farber, Martin; Jamison, Robert E. (1986), „Wypukłość na wykresach i hipergrafach”, SIAM Journal on Algebraic and Discrete Methods , 7 (3): 433–444, doi : 10,1137/0607049 , hdl : 10338.dmlcz/127659 , MR 0844046 .
•   Glasserman, Paweł; Yao, David D. (1994), Monotone Structure in Discrete Event Systems , Wiley Series in Probability and Statistics, Wiley Interscience, ISBN 978-0-471-58041-6 .
•   Gordon, Gary (1997), „A β niezmiennik dla greedoidów i antymatroidów”, Electronic Journal of Combinatorics , 4 (1): Research Paper 13, doi : 10.37236/1298 , MR 1445628 .
•   Jamison, Robert (1980), „Copoints in antimatroids”, Proceedings of the XI Southeastern Conference on Combinatoryics, Graph Theory and Computing (Florida Atlantic Univ., Boca Raton, Fla., 1980), tom. II , Congressus Numerantium, t. 29, s. 535–544, MR 0608454 .
•    Kashiwabara, Kenji; Nakamura, Masataka; Okamoto, Yoshio (2005), „Twierdzenie o reprezentacji afinicznej dla abstrakcyjnych geometrii wypukłych”, Computational Geometry , 30 (2): 129–144, CiteSeerX 10.1.1.14.4965 , doi : 10.1016/j.comgeo.2004.05.001 , MR 2107032 .
•    Kempner, Julia; Levit, Vadim E. (2003), „Korespondencja między dwiema charakterystykami algorytmów antymatroidów” , Electronic Journal of Combinatorics , 10 : Research Paper 44, arXiv : math/0307013 , Bibcode : 2003math......7013K , doi : 10.37236/ 1737 , MR 2014531 , S2CID 11015967
•   Knauer, Kolja (2009), „Wypalanie wiórów, antymatroidy i wielościany”, Europejska konferencja na temat kombinatoryki, teorii grafów i zastosowań (EuroComb 2009) , Elektroniczne notatki w matematyce dyskretnej, tom. 34, s. 9–13, doi : 10.1016/j.endm.2009.07.002 , MR 2591410
•   Korte, Bernhard ; Lovász, László ; Schrader, Rainer (1991), Greedoids , Springer-Verlag, s. 19–43, ISBN 3-540-18190-3 .
•   Kupiec, Nazarré; Riggle, Jason (2016), „Gramatyka OT, poza zamówieniami częściowymi: zestawy ERC i antymatroidy” , Natural Language & Linguistic Theory , 34 : 241–269, doi : 10.1007/s11049-015-9297-5 , S2CID 170567540 .
•   Monjardet, Bernard (1985), „Zastosowanie do częstego ponownego odkrywania pojęcia”, Order , 1 (4): 415–417, doi : 10.1007 / BF00582748 , S2CID 119378521 .
• Parmar, Aarati (2003), „Niektóre struktury matematyczne leżące u podstaw efektywnego planowania” , Wiosenne sympozjum AAAI na temat logicznej formalizacji zdroworozsądkowego rozumowania (PDF) .