Bitangenty kwarcu

Krzywa Trotta i siedem jej bitangentów. Pozostałe są symetryczne względem obrotu o 90° przez początek układu współrzędnych.

Krzywa Trotta ze wszystkimi 28 bitangentami.

W teorii algebraicznych krzywych płaskich ogólna krzywa płaszczyzny kwartalnej ma 28 linii dwustycznych , które są styczne do krzywej w dwóch miejscach. Linie te istnieją na zespolonej płaszczyźnie rzutowej , ale możliwe jest zdefiniowanie krzywych kwartalnych, dla których wszystkie 28 z tych linii mają jako współrzędne liczby rzeczywiste , a zatem należą do płaszczyzny euklidesowej .

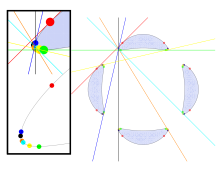
Wyraźny quartic z dwudziestoma ośmioma rzeczywistymi bitangentami został po raz pierwszy podany przez Plückera ( 1839 ). utworzone przez miejsce środków elips o ustalonych długościach osi, stycznych do dwóch nierównoległych linii. Shioda (1995) podał inną konstrukcję kwarcu z dwudziestoma ośmioma bitangentami, utworzonymi przez rzutowanie powierzchni sześciennej ; dwadzieścia siedem bitangentów krzywej Shiody jest rzeczywistych, podczas gdy dwudziesta ósma to linia w nieskończoności na płaszczyźnie rzutowej.

Przykład

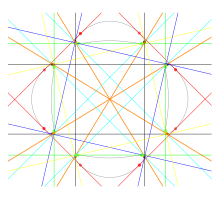
Krzywa Trotta , kolejna krzywa z 28 rzeczywistymi bitangentami, to zbiór punktów ( x , y ) spełniających równanie wielomianu czwartego stopnia

${\ Displaystyle \ Displaystyle 144 (x ^ {4} + y ^ {4}) -225 ( x^{2}+y^{2})+350x^{2}y^{2}+81=0.}$

Punkty te tworzą nieosobliwą krzywą kwarcową, która ma rodzaj trzeci i która ma dwadzieścia osiem rzeczywistych bitangentów .

Podobnie jak przykłady Plückera oraz Bluma i Guinanda, krzywa Trotta ma cztery oddzielne owale, maksymalną liczbę dla krzywej stopnia czwartego, a zatem jest krzywą M. Cztery owale można pogrupować w sześć różnych par owali; dla każdej pary owali istnieją cztery bitangenty dotykające obu owali w parze, dwa oddzielające dwa owale i dwa, które tego nie robią. Dodatkowo każdy owal ogranicza niewypukły obszar płaszczyzny i ma jeden bitangent obejmujący niewypukłą część jego granicy.

Połączenia z innymi strukturami

Podwójna krzywa do krzywej kwartalnej ma 28 rzeczywistych zwykłych podwójnych punktów, podwójnych do 28 bitangentów krzywej pierwotnej.

28 bitangentów kwarcu można również umieścić zgodnie z symbolami postaci

$Displaystyle {\ rozpocząć {bmatrix} a & b & c \\ d & e & f \\\ koniec {bmatrix}}}$

gdzie a, b, c, d, e, f to zero lub jeden i gdzie

${\ reklama w stylu displayowym + być + cf = 1 \ (\ nazwa operatora {mod} \ 2).}$

Istnieje 64 opcji dla a, b, c, d, e, f , ale tylko 28 z nich daje nieparzystą sumę. Można również interpretować a, b, c jako jednorodne współrzędne punktu płaszczyzny Fano , a d, e, f jako współrzędne prostej w tej samej skończonej płaszczyźnie rzutowej; warunek, że suma jest nieparzysta, jest równoważny wymaganiu, aby punkt i prosta się nie stykały, a istnieje 28 różnych par punktu i prostej, które się nie stykają.

Punkty i linie płaszczyzny Fano, które są rozłączne z nieincydentalną parą punkt-linia, tworzą trójkąt, a bitangenty kwarty zostały uznane za odpowiadające 28 trójkątom płaszczyzny Fano. Wykres Leviego płaszczyzny Fano to wykres Heawooda , w którym trójkąty płaszczyzny Fano są reprezentowane przez 6 cykli. Z kolei 28 6-cykli grafu Heawooda odpowiada 28 wierzchołkom grafu Coxetera .

28 bitangentów kwarcu odpowiada również parom 56 linii na powierzchni del Pezzo stopnia 2 i 28 nieparzystym cechom theta .

27 linii sześciennych i 28 bitangentów kwarty, razem ze 120 trójkątnymi płaszczyznami kanonicznej sekstycznej krzywej rodzaju 4, tworzą „ trójcę ” w sensie Vladimira Arnolda , a konkretnie formę korespondencji McKaya i mogą być powiązany z wieloma innymi przedmiotami, w tym E ₇ i E ₈ , jak omówiono na trójcach .

Notatki

• Blum R.; Guinand, AP (1964). „Kwartyk z 28 rzeczywistymi bitangentami” . Kanadyjski Biuletyn Matematyczny . 7 (3): 399–404. doi : 10.4153/cmb-1964-038-6 .
• Cayley, Arthur (1879), „O bitangentach kwarcu”, Salmon's Higher Plane Curves , s. 387–389 . W Zgromadzonych artykułach matematycznych Arthura Cayleya , Andrew Russell Forsyth, red., The University Press, 1896, tom. 11, s. 221–223.
•    Gray, Jeremy (1982), „Z historii prostej grupy”, The Mathematical Intelligencer , 4 (2): 59–67, doi : 10.1007 / BF03023483 , MR 0672918 , S2CID 14602496 . Przedruk w    Levy, Silvio, wyd. (1999), Ośmioraka droga , MSRI Publications, tom. 35, Cambridge University Press, s. 115–131, ISBN 0-521-66066-1 , MR 1722415 .
•   Manivel, L. (2006), „Konfiguracje linii i modeli algebr Liego”, Journal of Algebra , 304 (1): 457–486, arXiv : math/0507118 , doi : 10.1016/j.jalgebra.2006.04.029 , S2CID 17374533 .
• McKay, John; Sebbar, Abdellah (2007). „Funkcje replikowalne: wprowadzenie”. Granice w teorii liczb, fizyce i geometrii II : 373–386. doi : 10.1007/978-3-540-30308-4_10 .
• Plücker, J. (1839), Theorie der algebraischen Curven: gegrundet auf eine neue Behandlungsweise der analytischen Geometrie , Berlin: Adolph Marcus .
• Riemann, GFB (1876), "Zur Theorie der Abel'schen Funktionen für den Fall p = 3", Ges. Werke , Lipsk, s. 456–472 . Cytowane przez Cayleya.
•   Shioda, Tetsuji (1995), „Transformacje Weierstrassa i powierzchnie sześcienne” (PDF) , Commentarii Mathematici Universitatis Sancti Pauli , 44 (1): 109–128, MR 1336422
• Trott, Michael (1997), „Zastosowanie GroebnerBasis do trzech problemów w geometrii”, Mathematica in Education and Research , 6 (1): 15–28 .