Funkcja znaku zapytania Minkowskiego

Funkcja znaku zapytania Minkowskiego.

Po lewej: ?( x ) . Prawo: ?( x ) − x .

W matematyce funkcja znaku zapytania Minkowskiego , oznaczona ?( x ) , jest funkcją o niezwykłych właściwościach fraktalnych , zdefiniowaną przez Hermanna Minkowskiego w 1904 r. Odwzorowuje kwadratowe liczby niewymierne na liczby wymierne w przedziale jednostkowym , za pomocą wyrażenia odnoszącego się do ciągłości rozwinięcia ułamkowe kwadratów do rozwinięć binarnych liczb wymiernych, podane przez Arnauda Denjoya w 1938 r. Odwzorowuje również liczby wymierne na liczby wymierne w diadzie , co widać na podstawie rekurencyjnej definicji ściśle związanej z drzewem Sterna – Brocota .

Definicja i intuicja

Jeden ze sposobów definiowania funkcji znaku zapytania obejmuje zgodność między dwoma różnymi sposobami przedstawiania liczb ułamkowych przy użyciu skończonych lub nieskończonych sekwencji binarnych . Najbardziej znany ciąg zer i jedynek z pojedynczym znakiem „.”, na przykład „11.001001000011111…” można interpretować jako binarną reprezentację liczby . W tym przypadku jest to liczba

$${\ Displaystyle 2 + 1 + {\ Frac {1} {8}} + {\ Frac {1} {64}} + \ cdots = \ pi.}$$

Istnieje jednak inny sposób interpretacji tej samej sekwencji przy użyciu ułamków ciągłych . Interpretując część przed punktem jako liczbę binarną w ten sam sposób, zastąp każdy kolejny blok zer lub jedynek po punkcie jego długością przebiegu , w tym przypadku generując sekwencję ${\ Displaystyle [3; 2,1,2,1,4,5, \ kropki]}$ . Następnie użyj tej sekwencji jako współczynników ułamka ciągłego:

$${\ Displaystyle 3 + {\ Frac {1} {\ Displaystyle 2 + {\ Frac {1} {\ Displaystyle 1 + {\ Frac {1} {\ Displaystyle 2+ {\ Frac {1} {\ Displaystyle 1+ {\ Frac {1} {\ Displaystyle 4 + {\ Frac {1} {\ Displaystyle 5+ \ kropki}}}} }}}}}}}}\około 3,365}$$

Funkcja znaku zapytania odwraca ten proces: tłumaczy ułamek ciągły danej liczby rzeczywistej na sekwencję binarną zakodowaną w długości serii, a następnie ponownie interpretuje tę sekwencję jako liczbę binarną. Na przykład dla powyższego przykładu ${\ Displaystyle \ nazwa operatora {?} (3,365 \ kropki) = \ pi}$ . Aby zdefiniować to formalnie, jeśli liczba niewymierna ma (niekończącą się) reprezentację ułamka ciągłego ${\ displaystyle x}$

$${\ Displaystyle x = a_ {0} + {\ Frac {1} {\ Displaystyle a_ {1} + {\ Frac {1} {\ Displaystyle a_ {2} + \ cdots}} }}=[a_{0};a_{1},a_{2},\kropki ]}$$

wtedy wartość funkcji znaku zapytania na $jest$ jako wartość nieskończonego szeregu

$${\ Displaystyle \ nazwa operatora {?} (x) = a_ {0} + 2 \ suma _ {n = 1} ^ {\ infty} {\ Frac {\ lewo (-1 \ prawo) ^ {n + 1}} {2^{a_{1}+\cdots +a_{n}}}}.}$$

${\ Displaystyle [a_ {0}; a_ {1}, a_ {2}, \ kropki, a_ {m}]}$ , jeśli $[$ wymierna ma końcową reprezentację ułamka ciągłego to wartość funkcji znaku zapytania na ${\ displaystyle x}$ to skończona suma,

$${\ Displaystyle \ nazwa operatora {?} (x) = a_ {0} + 2 \ suma _ {n = 1} ^ {m} {\ Frac {\ lewo (-1 \ prawo) ^ {n + 1}} 2^{a_{1}+\cdots +a_{n}}}}.}$$

Analogicznie do sposobu, w jaki funkcja znaku zapytania reinterpretuje ułamki ciągłe jako liczby binarne, funkcję Cantora można rozumieć jako reinterpretację liczb trójskładnikowych jako liczb binarnych.

Samosymetria

Znak zapytania jest wyraźnie wizualnie samopodobny. Monoid samopodobieństw może być generowany przez dwa operatory S i R działające na kwadracie jednostkowym i zdefiniowany w następujący sposób :

$${\ Displaystyle {\ rozpocząć {wyrównane} S (x, y) & = \ lewo ({\ Frac {x} {x + 1}}, {\ Frac {y} {2}} \ prawej), \\[ 5px]R(x,y)&=(1-x,1-y).\end{wyrównane}}}$$

Wizualnie S zmniejsza kwadrat jednostki do lewej dolnej ćwiartki, podczas gdy R wykonuje odbicie punktowe przez jego środek.

Punkt na wykresie ? ma współrzędne ( x , ?( x )) dla pewnego x w przedziale jednostkowym. Taki punkt jest przekształcany przez S i R w inny punkt grafu, ponieważ ? spełnia następujące tożsamości dla wszystkich x ∈ [0, 1] :

$${\ Displaystyle {\ rozpocząć {wyrównane} \ nazwa operatora {?} \ lewo ({\ Frac {x} {x + 1}} \ prawo) & = {\ Frac {\ nazwa operatora {?} (x)} {2} },\\[5px]\nazwa_operatora {?} (1-x)&=1-\nazwa_operatora {?} (x).\end{wyrównane}}}$$

Te dwa operatory mogą być wielokrotnie łączone, tworząc monoid. Ogólny element monoidu jest wtedy

$${\ Displaystyle S ^ {a_ {1}} RS ^ {a_ {2}} RS ^ {a_ {3}} \ cdots}$$

dla dodatnich liczb całkowitych a ₁ , a ₂ , a ₃ , … . Każdy taki element opisuje samopodobieństwo funkcji znaku zapytania. Ten monoid jest czasami nazywany monoidem podwajającym okres , a wszystkie krzywe fraktalne podwajające okres mają opisaną przez siebie samosymetrię ( kategorią takich krzywych jest krzywa de Rhama , której szczególnym przypadkiem jest znak zapytania). Elementy monoidu są zgodne z wymiernymi za pomocą identyfikacji a ₁ , a ₂ , a ₃ , … z ułamkiem ciągłym [0; za ₁ , za ₂ , za ₃ ,…] . Od kiedy oboje

$${\ Displaystyle S: x \ mapsto {\ Frac {x} {x + 1}}}$$

I

$${\ Displaystyle T: x \ mapsto 1-x}$$

są liniowymi przekształceniami ułamkowymi o współczynnikach całkowitych, monoid można traktować jako podzbiór grupy modułowej PSL(2, Z ) .

Kwadratowe irracjonalne

Funkcja znaku zapytania zapewnia odwzorowanie jeden do jednego z niediadycznych liczb wymiernych na kwadratowe liczby irracjonalne , umożliwiając w ten sposób wyraźny dowód policzalności tych ostatnich. W rzeczywistości można to rozumieć jako odpowiadające orbitom okresowym dla transformacji diadycznej . Można to wyraźnie wykazać w zaledwie kilku krokach.

Symetria diadyczna

Zdefiniuj dwa ruchy: ruch w lewo i ruch w prawo, obowiązujące w przedziale jednostkowym ${\ Displaystyle 0 \ równoważnik x \ równoważnik 1$ }

$${\ Displaystyle L_ {D} (x) = {\ Frac {x} {2}}}$$

i ${\ Displaystyle L_ {C} (x) = {\ Frac {x} {1 + x}}}$ i

$${\ Displaystyle R_ {D} (x) = {\ Frac {1 + x} {2}}}$$

i ${\ Displaystyle R_ {C} (x) = {\ Frac {1} {2-x}}}$ Funkcja znaku zapytania jest wtedy zgodna z symetrią ruchu w lewo

$${\ Displaystyle L_ {D} \ circ ? =? \ circ L_ {C}}$$

i symetrię ruchu w prawo

$${\ Displaystyle R_ {D} \ circ ? =? \ circ R_ {C}}$$

gdzie ${\ displaystyle \ circ}$ oznacza skład funkcji . Można je dowolnie łączyć. Rozważmy na przykład sekwencję ruchów lewo-prawo ${\ displaystyle LRLLR.}$ Dodając indeksy dolne C i D oraz, dla jasności, usuwając operator kompozycji we wszystkich miejscach z wyjątkiem kilku, mamy: ${\ displaystyle \ circ }$

$${\ Displaystyle L_ {D} R_ {D} L_ {D} L_ {D} R_ {D} \ circ? =? \ circ L_ {C} R_ {C} L_ {C}L_{C}R_{C}}$$

Dowolne ciągi o skończonej długości w literach L i R odpowiadają diadycznym wymiernym w tym sensie, że każdy wymierny diadyczny można zapisać zarówno jako liczbę całkowitą n , jak i ${\ Displaystyle y = n/2 ^ {m}}$ m i jako skończona długość bitów ${\ Displaystyle y = 0.b_ {1} b_ {2} b_ {3} \ cdots b_ {m}}$ z ${\ displaystyle b_ {k} \ in \ {0,1 \}.}$ Zatem każdy wymierny diadyczny jest w relacji jeden do jednego z pewną samosymetrią funkcji znaku zapytania.

Niektóre zmiany w notacji mogą nieco ułatwić wyrażenie powyższego. Niech ${\ displaystyle g_ {1}$ i $}$ oznaczają L i R. Kompozycja funkcji rozciąga to na monoid , ponieważ można napisać ${\ displaystyle g_ {010}= g_ {0} g_ {1} g_ {0}}$ i ogólnie $} g_ {B} = g_ {AB}}$ dla niektórych ciągów binarnych cyfr A , B , gdzie AB jest zwykłą konkatenacją takich ciągów. Diadyczny monoid M jest zatem monoidem wszystkich takich ruchów lewo-prawo o skończonej długości. Pisząc jako ogólny element monoidu, istnieje odpowiednia samosymetria funkcji znaku zapytania: ${\ displaystyle \ gamma \ in M}$

$${\ Displaystyle \ gamma _ {D} \ circ? =? \ circ \ gamma _ {C}}$$

izomorfizm

Wyraźne odwzorowanie między wymiernymi a diadycznymi wymiernymi można uzyskać, dostarczając operator odbicia

$${\ Displaystyle r (x) = 1-x}$$

i zauważając, że oba

$${\ Displaystyle r \ circ R_ {D} \ circ r = L_ {D}}$$

i $\ Displaystyle r \ circ R_ {C} \ circ r = L_ {C}}$ Ponieważ ${\ Displaystyle r ^ {2} = 1} jest$ , an dowolny ciąg ruchów lewo-prawo można przepisać jako ciąg ruchów tylko w lewo, po których następuje odbicie, po którym następuje więcej ruchów w lewo, odbicie itd., czyli jako ${\ Displaystyle L ^ {a_ {1}} rL ^ {a_ {2}} rL ^ {a_ {3}} \ cdots}, co jest$ wyraźnie izomorficzne z ${\ Displaystyle S^{a_{1}}TS^{a_{2}}TS^{a_{3}}\cdots }$ z góry. $pewną$ wyraźną pod $,$ _ wyraźnie jest równe ${\ Displaystyle y = 0.b_ {1} b_ {2} b_ {3} \ cdots b_ {m}}$ gdzie każdy ${\ Displaystyle b_ {k}\in \{0,1\}}$ jest bitem binarnym, zero odpowiada ruchowi w lewo, a jeden odpowiada ruchowi w prawo. Równoważna sekwencja $}}$ oceniana na $L_ {C}, R_$ daje liczbę wymierną $q$$\ Displaystyle p / q = [a_ {1}$ , pamiętając, że jest to ciąg wymierny, ponieważ ciąg ${\ Displaystyle (a_ {1}, a_ {2}, a_ {3}, \ cdots, a_ {j})}$ miał skończoną długość. Ustanawia to zgodność jeden do jednego między diadycznymi wymiernymi a wymiernymi.

Okresowe orbity transformacji diadycznej

Rozważmy teraz okresowe orbity transformacji diadycznej . Odpowiadają one sekwencjom bitów składającym się ze skończonej początkowej „chaotycznej” sekwencji bitów ${\ Displaystyle b_ {0}, b_ {1}, b_ {2}, \ cdots ,b_{k-1}}$ , po których następuje powtarzający się łańcuch ${\ Displaystyle b_ {k}, b_ {k + 1}, b_ {k + 2}, \ cdots, b_ {k + m-1}} długości m {\$ Displaystyle $}$ . Takie powtarzające się ciągi odpowiadają liczbie wymiernej. Można to łatwo wyjaśnić. Pisać

$${\ Displaystyle y = \ suma _ {j = 0} ^ {m-1} b_ {k + j} 2 ^ {-j-1} }$$

wtedy wyraźnie ma

$${\ Displaystyle \ suma _ {j = 0} ^ {\ infty} b_ {k + j }2^{-j-1}=y\suma _{j=0}^{\infty }2^{-jm}={\frac {y}{1-2^{m}}}}$$

Biorąc pod uwagę początkową, niepowtarzającą się sekwencję, wyraźnie mamy liczbę wymierną. W rzeczywistości każdą liczbę wymierną można wyrazić w ten sposób: początkowa „losowa” sekwencja, po której następuje cykliczne powtórzenie. Oznacza to, że okresowe orbity mapy są w relacji jeden do jednego z wymiernymi.

Okresowe orbity jako ułamki ciągłe

Takie okresowe orbity mają równoważny okresowy ułamek ciągły, zgodnie z izomorfizmem ustalonym powyżej. Istnieje początkowa „chaotyczna” orbita o skończonej długości, po której następuje powtarzająca się sekwencja. Powtarzająca się sekwencja generuje okresowy ułamek ciągły spełniający ${\ Displaystyle x = [a_ {n}, a_ {n + 1}, a_ {n + 2}, \ cdots, a_ {n + r}, x].} Ten ciągły ułamek ma$ postać

$${\ Displaystyle x = {\ Frac {\ alfa x + \ beta} {\ gamma x + \ delta}}}$$

gdzie ${\ Displaystyle \ alfa, \ beta, \ gamma, \ delta}$ to liczby całkowite i spełniające ${\ Displaystyle \ alfa \ delta - \ beta \ gamma =\pm 1.}$ Jawne wartości można uzyskać pisząc

$${\ Displaystyle S \ mapsto {\ rozpocząć {pmatrix} 1 i 0 \\ 1 i 1 \ koniec {pmatrix}}}$$

na zmianę, tak

$${\ Displaystyle S ^ {n} \ mapsto {\ rozpocząć {pmatrix} 1 i 0 \\ n i 1 \ koniec {pmatrix}}}$$

podczas gdy odbicie jest podane przez

$${\ Displaystyle T \ mapsto {\ rozpocząć {pmatrix} -1 i 1 \\ 0 i 1 \ koniec {pmatrix}}}$$

tak, że ${\ displaystyle T ^ {2} = ja}$ . Obie te macierze są jednomodułowe , dowolne iloczyny pozostają jednomodułowe i dają macierz postaci

$${\ Displaystyle S ^ {a_ {n}} TS ^ {a_ {n + 1}} T \ cdots TS ^ {a_{n+r}}={\begin{pmatrix}\alpha &\beta \\\gamma &\delta \end{pmatrix}}}$$

podając dokładną wartość ułamka ciągłego. Ponieważ wszystkie wpisy macierzy są liczbami całkowitymi, macierz ta należy do rzutowej grupy modułowej ${\ Displaystyle PSL (2, \ mathbb {Z}).}$

γ ${\ Displaystyle \ gamma x ^ {2} + (\ delta - \ alfa) x- \ beta =$ } trudno zweryfikować, czy rozwiązania tego spełniają definicję kwadratowych liczb niewymiernych. W rzeczywistości każdy niewymierny kwadrat można wyrazić w ten sposób. Zatem niewymierne liczby kwadratowe są w relacji jeden do jednego z okresowymi orbitami transformaty diadycznej, które są w korespondencji jeden do jednego z (nie-diadycznymi) liczbami wymiernymi, które są w korespondencji jeden do jednego z racjonały diadyczne. Funkcja znaku zapytania zapewnia zgodność w każdym przypadku.

Właściwości ?( x )

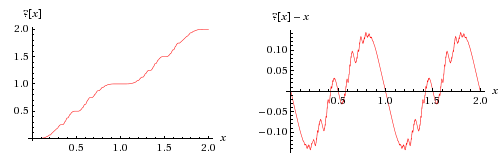
Funkcja znaku zapytania jest funkcją ściśle rosnącą i ciągłą, ale nie absolutnie ciągłą . Pochodna jest zdefiniowana ${\ displaystyle + \ infty}$ wszędzie i może przyjmować tylko dwie wartości: 0 (jej wartość prawie wszędzie, w tym wszystkie liczby wymierne ) i + . Istnieje kilka konstrukcji miary , która po zintegrowaniu daje funkcję znaku zapytania. Jedną z takich konstrukcji uzyskuje się mierząc gęstość liczb Fareya na rzeczywistej linii liczbowej. Miara znaku zapytania jest prototypowym przykładem tego, co czasami określa się jako miary multifraktalne .

Funkcja znaku zapytania odwzorowuje liczby wymierne na diadyczne liczby wymierne , czyli te, których reprezentacja o podstawie dwóch kończy się, co można udowodnić przez indukcję z konstrukcji rekurencyjnej opisanej powyżej. Odwzorowuje kwadratowe liczby niewymierne na niediadyczne liczby wymierne. W obu przypadkach zapewnia izomorfizm porządku między tymi zbiorami, konkretyzując twierdzenie Cantora o izomorfizmie, zgodnie z którym każde dwa nieograniczone policzalne gęste rzędy liniowe są izomorficzne rzędu. Jest to funkcja nieparzysta i spełnia równanie funkcyjne ?( x + 1) = ? ( x ) + 1 ; w konsekwencji x ↦ ?( x ) − x jest nieparzystą funkcją okresową z okresem jeden. Jeśli ?( x ) jest irracjonalne, to x jest albo algebraiczne stopnia większego niż dwa, albo transcendentalne .

Funkcja znaku zapytania ma 1/2 i 1 oraz co najmniej dwa kolejne, symetryczne stałe punkty w punktach 0, względem punktu środkowego. Jeden to około 0,42037. Moshchevitin przypuszczał, że były to jedyne 5 stałych punktów.

W 1943 roku Raphaël Salem postawił pytanie, czy współczynniki Fouriera – Stieltjesa funkcji znaku zapytania znikają w nieskończoności. Innymi słowy, chciał wiedzieć, czy

$${\ Displaystyle \ lim _ {n \ do \ infty} \ int _ {0} ^ {1} e ^ {2 \ pi inx} \ \ operatorname {d?} (x) = 0.}$$

Odpowiedzieli twierdząco na to Jordan i Sahlsten, jako szczególny przypadek wyniku na miarach Gibbsa .

Wykres funkcji znaku zapytania Minkowskiego jest szczególnym przypadkiem krzywych fraktalnych, zwanych krzywymi de Rhama .

Algorytm

Definicja rekurencyjna naturalnie nadaje się do algorytmu obliczania funkcji z dowolnym pożądanym stopniem dokładności dla dowolnej liczby rzeczywistej, jak pokazuje poniższa funkcja C. Algorytm schodzi z drzewa Sterna-Brocota w poszukiwaniu danych wejściowych x i po drodze sumuje warunki rozwinięcia binarnego y = ?( x ) . Dopóki niezmiennik pętli qr − ps = 1 pozostaje spełniony, nie ma potrzeby zmniejszania ułamka m / n = p + r / q + s , ponieważ jest już w najniższych kategoriach. Innym niezmiennikiem jest p / q ≤ x < r / s . Pętla for w tym programie może być analizowana trochę jak jakiś czas pętli, z warunkowymi instrukcjami break w pierwszych trzech wierszach określającymi warunek. Jedyne instrukcje w pętli, które mogą mieć wpływ na niezmienniki, znajdują się w dwóch ostatnich wierszach i można wykazać, że zachowują one prawdziwość obu niezmienników, o ile pierwsze trzy wiersze zostały wykonane pomyślnie bez wychodzenia z pętli. Trzecim niezmiennikiem treści pętli (do dokładności zmiennoprzecinkowej) jest y ≤ ?( x ) < y + d , ale ponieważ d jest zmniejszone o połowę na początku pętli, przed sprawdzeniem jakichkolwiek warunków, nasz wniosek jest tylko taki, że y ≤ ?( x ) < y + 2 d na końcu pętli.

Aby udowodnić terminację , wystarczy zauważyć, że suma q + s zwiększa się o co najmniej 1 z każdą iteracją pętli i że pętla zakończy się, gdy ta suma będzie zbyt duża, aby mogła być reprezentowana w pierwotnym typie danych C long . Jednak w praktyce przerwanie warunkowe, gdy y + d == y jest tym, co zapewnia zakończenie pętli w rozsądnym czasie.

   
       
                 
          
         /* Funkcja znaku zapytania Minkowskiego */  double  minkowski  (  double  x  )  {  long  p  =  x  ;  długie  q  =  1  ,  r  =  p  +  1  ,  s  =  1  ,  m  ,  n  ;  podwójne  re  =  1  ,  y  =  p  ;  jeśli  (  x  <  p  ||    0    0
          
       
          
             
             
            
          (  p  <  )  ^  (  r  <=  ))  powrót  x  ;  /* poza zakresem ?(x) =~ x */  for  (;;)  {  /* niezmienniki: q * r - p * s == 1 && p / q <= x && x < r / s */  d  /=  2  ;  jeśli  (  y  +  re  ==  y  )  przerwać  ;  /* osiągnięto maksymalną możliwą precyzję */  m  =  p  +  r  ;  jeśli  ((   0    0
             
            
           0
             

              
              
              
           m  <  )  ^  (  p  <  ))  przerwać  ;  /* suma przepełniona */  n  =  q  +  s  ;  jeśli  (  n  <  )  przerwij  ;  /* suma przepełniona */  if  (  x  <  (  podwójna  )  m  /  n  )  {  r  =  m  ;  s  =  n  ;  }  jeszcze  { 
              
              
              
        
    
        
 y  +=  re  ;  p  =  m  ;  q  =  n  ;  }  }  zwróć  y  +  d  ;  /* końcowe zaokrąglenie */  } 

Rozkład prawdopodobieństwa

Ograniczając funkcję znaku zapytania Minkowskiego do ?:[0,1] → [0,1], można jej użyć jako funkcji dystrybucji skumulowanej rozkładu osobliwego w przedziale jednostkowym. Ten rozkład jest symetryczny względem swojego punktu środkowego, z surowymi momentami około m ₁ = 0,5, m ₂ = 0,290926, m ₃ = 0,186389 i m ₄ = 0,126992, a więc średnia i mediana 0,5, odchylenie standardowe około 0,2023, a skośność 0 i nadmiar kurtozy około -1,147.

Zobacz też

• Pochodna Pompeju

źródła historyczne

•   Minkowski, Hermann (1904), "Zur Geometrie der Zahlen" , Verhandlungen des III. internationalen Mathematiker-Kongresses in Heidelberg , Berlin, s. 164–173, JFM 36.0281.01 , zarchiwizowane od oryginału w dniu 4 stycznia 2015 r.
•   Denjoy, Arnaud (1938), „Sur une funkction réelle de Minkowski”, J. Math. Pures Appl. , Série IX (w języku francuskim), 17 : 105–151, Zbl 0018.34602

Bibliografia

•    Alkauskas, Giedrius (2010), „Momenty funkcji znaku zapytania Minkowskiego: funkcja okresu diadycznego”, Glasgow Mathematical Journal , 52 (1): 41–64, arXiv : 0801,0051 , doi : 10,1017/S0017089509990152 , MR 2587817 , S2CID 1151 67042
•    Bhattacharjee, Meenaxi; Macpherson, Dugald; Möller, Rögnvaldur G.; Neumann, Peter M. (1997), „Liczby wymierne”, Uwagi o nieskończonych grupach permutacji , Teksty i odczyty z matematyki, tom. 12, Berlin: Springer-Verlag, s. 77–86, doi : 10.1007/978-93-80250-91-5_9 , ISBN 81-85931-13-5 , MR 1632579
•    Duszistowa, Anna A.; Moshchevitin, Nikolai G. (marzec 2012), „O pochodnej funkcji znaku zapytania Minkowskiego ${\ Displaystyle? (x)}$ „, Journal of Mathematical Sciences , 182 (4): 463–471, arXiv : 0706.2219 , doi : 10.1007/s10958-012-0750-2 , MR 2825515 , S2CID 115156022
•    Finch, Steven R. (2003), Stałe matematyczne , Encyklopedia matematyki i jej zastosowań, tom. 94, Cambridge : Cambridge University Press , ISBN 978-0-521-81805-6 , Zbl 1054.00001
•   Girgensohn, Roland (1996), „Konstruowanie funkcji osobliwych za pomocą ułamków Fareya”, Journal of Mathematical Analysis and Applications , 203 (1): 127–141, doi : 10.1006 / jmaa.1996.0370 , MR 1412484
•   Jordania, Tomasz; Sahlsten, Tuomas (2016), „Fourier Transformations of Gibbs Mierzy dla mapy Gaussa”, Mathematische Annalen , 364 ( 3–4): 983–1023, Arxiv : 1312.3619 , Bibcode : 2013Arxiv1312.3619J , doi -1241-9 , S2CID 56046793
•   Khinchin, A. Ya. (1964) [Pierwotnie opublikowane w języku rosyjskim, 1935], „10: Kwadratowe liczby niewymierne i okresowe ułamki ciągłe”, Continued Fractions , University of Chicago Press , s. 47–50, ISBN 0-486-69630-8 ; przedrukowane przez Dover Publications, 1997
• Moshchevitin, Nikolay (25 listopada 2020), „Sesja otwartych problemów”, Diophantine Problems, Determinism and Randomness , CIRM – przez YouTube
•    Pyteas Fogg, N. (2002), Berthé, Valérie ; Ferenczi, Sébastien; Mauduit, chrześcijanin; Siegel, A. (red.), Podstawienia w dynamice, arytmetyce i kombinatoryce , Lecture Notes in Mathematics, tom. 1794, Berlin: Springer-Verlag , ISBN 978-3-540-44141-0 , Zbl 1014.11015
•   Salem, Raphaël (1943), „O niektórych osobliwych funkcjach monotonicznych, które są ściśle rosnące” (PDF) , Transactions of the American Mathematical Society , 53 (3): 427–439, doi : 10,2307/1990210 , JSTOR 1990210

Dalsza lektura

• Alkauskas, Giedrius (2008), Transformacje całkowe funkcji znaku zapytania Minkowskiego , rozprawa doktorska, University of Nottingham
•   Bibiloni, L.; Paradis, J.; Viader, P. (1998), „Nowe światło na funkcję ?(x) Minkowskiego” , Journal of Number Theory , 73 (2): 212–227, doi : 10.1006/jnth.1998.2294 , hdl : 10230/843 , Zbl 0928.11006 , zarchiwizowane od oryginału w dniu 22 czerwca 2015 r
•   Bibiloni, L.; Paradis, J.; Viader, P. (2001), „Pochodna funkcji osobliwej Minkowskiego”, Journal of Mathematical Analysis and Applications , 253 (1): 107–125, doi : 10.1006/jmaa.2000.7064 , Zbl 0995.26005
• Conley, RM (2003), A Survey of the Minkowski ?(x) Function , praca magisterska, West Virginia University
• Conway, JH (2000), „Wykrzywione ułamki”, O liczbach i grach (wyd. 2), Wellesley, MA: AK Peters, s. 82–86
• Vepstas, L. (2004), Znak zapytania Minkowskiego i grupa modułowa SL (2, Z) (PDF)
• Vepstas, L. (2008), „Na miarę Minkowskiego”, arXiv : 0810,1265 [ math.DS ]

Linki zewnętrzne

• Obszerny spis bibliografii
• Weisstein, Eric W. , „Funkcja znaku zapytania Minkowskiego” , MathWorld
• Prosta implementacja IEEE 754 w C++