Funkcja Cantora

Wykres funkcji Cantora na przedziale jednostkowym

W matematyce funkcja Cantora jest przykładem funkcji ciągłej , ale nie absolutnie ciągłej . Jest to notoryczny kontrprzykład w analizie, ponieważ kwestionuje naiwne intuicje dotyczące ciągłości, pochodnej i miary. Chociaż jest ciągła wszędzie i prawie wszędzie ma pochodną zerową, jej wartość wciąż zmienia się od 0 do 1, gdy jej argument sięga od 0 do 1. Tak więc, w pewnym sensie funkcja wydaje się bardzo podobna do stałej, która nie może rosnąć, a w innym , rzeczywiście rośnie monotonicznie.

Jest również nazywany funkcją trójskładnikową Cantora , funkcją Lebesgue'a , funkcją pojedynczą Lebesgue'a , funkcją Cantora-Vitaliego , schodami diabła , funkcją schodową Cantora i funkcją Cantora-Lebesgue'a . Georg Cantor ( 1884 ) przedstawił funkcję Cantora i wspomniał, że Scheeffer wskazał, że jest to kontrprzykład dla rozszerzenia fundamentalnego twierdzenia rachunku różniczkowego, o którym mówił Harnack . Funkcję Cantora omówili i spopularyzowali Scheeffer (1884) , Lebesgue (1904) i Vitali (1905) .

Definicja

Iterowana konstrukcja funkcji Cantora

Aby zdefiniować funkcję Cantora , $: [0,1] \ do [$ będzie dowolną liczbą w ${\ Displaystyle [0,1]}$$Displaystyle$ i uzyskaj ${\ Displaystyle c (x)}$ , wykonując następujące czynności:

1. Wyraź w bazie 3. ${\ displaystyle x}$ .
2. Jeśli reprezentacja o podstawie 3 $\ displaystyle x}$ 1, zamień każdą cyfrę dokładnie po pierwszej 1 na 0. x {
3. Zamień pozostałe 2 na 1.
4. Zinterpretuj wynik jako liczbę binarną. Rezultatem jest ${\ Displaystyle c (x)}$ .

Na przykład:

• ${\ Displaystyle {\ tfrac {1} {4}}}$ ma trójskładnikową reprezentację 0,02020202 ... Nie ma jedynek, więc następny etap to nadal 0,02020202 ... To jest przepisane jako 0,01010101 ... To jest binarny reprezentacja ${\ Displaystyle {\ tfrac {1} {3}}}$ , więc ${\ Displaystyle c ({\ tfrac {1} {4}}) = {\ tfrac {1 }{3}}}$ .
• ${\ Displaystyle {\ tfrac {1} {5}}}$ ma trójskładnikową reprezentację 0,01210121 ... Cyfry po pierwszej 1 są zastępowane przez 0, aby uzyskać 0,01000000 ... To nie jest przepisywane, ponieważ nie ma dwójek. To jest binarna reprezentacja ${\ Displaystyle {\ tfrac {1} {4}}}$ , więc ${\ Displaystyle c ({\ tfrac {1} {5}}) = { \tfrac {1}{4}}}$ .
• $trójskładnikową$ reprezentację 0,21102 (lub 0,211012222 ... Cyfry po pierwszej 1 są zastępowane przez 0, aby uzyskać 0,21. Jest to przepisane jako 0,11. To jest binarna reprezentacja ${\ Displaystyle {\ tfrac {3} {4}}}$ , więc ${\ Displaystyle c ({\ tfrac {200} {243}}) = { \tfrac {3}{4}}}$ .

Równoważnie, jeśli $]$ jest ustawiony na [0,1 , to funkcja Cantora ${\ Displaystyle c: [0,1 ]\do [0,1]}$ można zdefiniować jako

${\ Displaystyle c (x) = {\ rozpocząć {przypadki} \ suma _ {n = 1} ^ {\ infty} {\ Frac {a_ {n}} {2 ^ {n}}}, & x = \ suma _ {n=1}^{\infty}{\frac {2a_{n}}{3^{n}}}\in {\mathcal {C}}\ \mathrm {for} \ a_{n}\in \ {0,1\};\\\sup _{y\równik x,\,y\in {\mathcal {C}}}c(y),&x\in [0,1]\setminus {\mathcal { C}}.\\\end{przypadki}}}$

Ta formuła jest dobrze zdefiniowana, ponieważ każdy element zbioru Cantora ma unikalną reprezentację o podstawie 3, która zawiera tylko cyfry 0 lub 2. (Dla niektórych członków trójskładnikowego rozwinięcia do {\ displaystyle {\ mathcal { $}}}$ powtarza się z końcowymi 2 i istnieje alternatywna niepowtarzająca się interpretacja kończąca się na 1. Na przykład ${\ Displaystyle {\ tfrac {1} {3}}}$ = 0,1 ₃ = 0,02222... ₃ jest członkiem zbiór Cantora). Ponieważ do $(0) = 0}$${\ Displaystyle c (1) = 1}$ i do i $\ Displaystyle c}$ jest monotoniczny na ${\ Displaystyle {\ mathcal {C}}}$ jasne jest, że ${\ Displaystyle 0 \ równoważnik c (x) \ równoważnik 1}$ dotyczy również wszystkich $\ Displaystyle x \ w [ 0,1]\setminus {\mathcal {C}}}$ .

Nieruchomości

, ${\textstyle c(x)}$ goes from 0 to 1 as Funkcja Cantora rzuca wyzwanie naiwnym intuicjom dotyczącym ciągłości i miary ; chociaż jest ciągły wszędzie i prawie wszędzie ma zerową pochodną $od$ ​​przechodzi goes from 0 to 1, and takes on every value in between. The Cantor function is the most frequently cited example of a real function that is uniformly continuous (precisely, it is Hölder continuous of exponent α = log 2/log 3) but not absolutely continuous. It is constant on intervals of the form (0.x₁x₂x₃...x_n022222..., 0.x₁x₂x₃...x_n200000...), and every point not in the Cantor set is in one of these intervals, so its derivative is 0 outside of the Cantor set. On the other hand, it has no derivative at any point in an uncountable subset of the Cantor set containing the interval endpoints described above.

Funkcję Cantora można również postrzegać jako skumulowaną funkcję rozkładu prawdopodobieństwa miary μ Bernoulliego 1/2-1/2 obsługiwanej na zbiorze Cantora: ${\ textstyle c (x) =\mu ([0,x])}$ . Ten rozkład prawdopodobieństwa, zwany rozkładem Cantora , nie ma części dyskretnej. Oznacza to, że odpowiednia miara jest bezatomowa . Dlatego w funkcji nie ma nieciągłości skokowych; każdy taki skok odpowiadałby atomowi w takcie.

Jednak żadnej niestałej części funkcji Cantora nie można przedstawić jako całki funkcji gęstości prawdopodobieństwa ; całkowanie dowolnej domniemanej funkcji gęstości prawdopodobieństwa , która nie jest prawie wszędzie równa zeru w dowolnym przedziale, da dodatnie prawdopodobieństwo pewnemu przedziałowi, do którego ten rozkład przypisuje prawdopodobieństwo zero. W szczególności, jak Vitali (1905) , funkcja nie jest całką swojej pochodnej, mimo że pochodna istnieje prawie wszędzie.

Funkcja Cantora jest standardowym przykładem funkcji pojedynczej .

Funkcja Cantora jest niemalejąca, a więc w szczególności jej wykres definiuje prostowalną krzywą . Scheeffer (1884) wykazał, że długość łuku jego wykresu wynosi 2.

Brak absolutnej ciągłości

Ponieważ miara Lebesgue'a nieprzeliczalnie nieskończonego zbioru Cantora wynosi 0, dla każdego dodatniego ε <1 i δ istnieje skończona sekwencja parami rozłącznych podprzedziałów o całkowitej długości < δ , nad którymi funkcja Cantora łącznie rośnie więcej niż ε .

W rzeczywistości dla każdego δ > 0 istnieje skończenie wiele parami rozłącznych przedziałów ( x _k , y _k ) (1 ≤ k ≤ M ) gdzie ${\ Displaystyle \ sum \ granice _ {k = 1} ^ {M} (y_ {k} -x_ {k}) <\ delta}$ i ${\ Displaystyle \sum \limits _{k=1}^{M}(c(y_{k})-c(x_{k}))=1}$ .

Alternatywne definicje

Konstrukcja iteracyjna

Poniżej definiujemy ciąg { f _n } funkcji na przedziale jednostkowym, który jest zbieżny do funkcji Cantora.

₀ Niech fa ( x ) = x .

Wtedy dla każdej liczby całkowitej n ≥ 0 następna funkcja f _{n +1} ( x ) zostanie zdefiniowana w kategoriach f _n ( x ) następująco:

Niech fa _{n +1} ( x ) = 1/2 × fa _n (3 x ) , gdy 0 ≤ x ≤ 1/3 ;

Niech f _{n +1} ( x ) = 1/2, gdy 1/3 ≤ x ≤ 2/3 ;

Niech fa _{n +1} ( x ) = 1/2 + 1/2 × fa _n (3 x - 2) , gdy 2/3 ≤ x ≤ 1 .

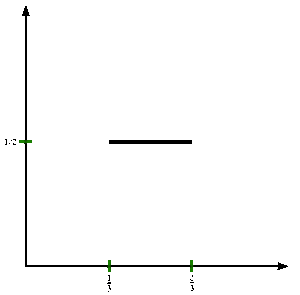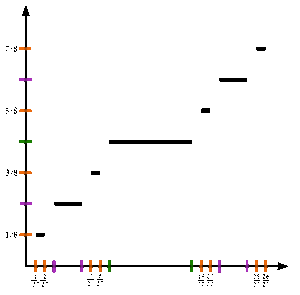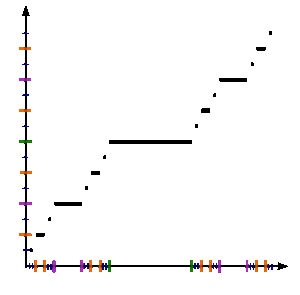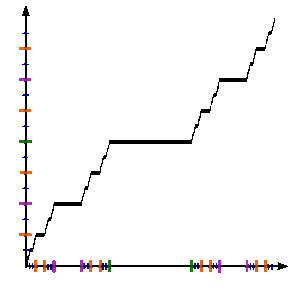
Te trzy definicje są zgodne w punktach końcowych 1/3 i 2/3, ponieważ f _n (0) = 0 i f _n (1) = 1 dla każdego n , przez indukcję. Można sprawdzić, że f _n zbiega się punktowo do zdefiniowanej powyżej funkcji Cantora. Ponadto zbieżność jest jednostajna. Rzeczywiście, rozdzielając na trzy przypadki, zgodnie z definicją f _{n +1} , widać to

${\ Displaystyle \ max _ {x \ w [0,1]} | f_ {n + 1} (x) -f_ {n} (x) | \ równoważnik {\ Frac {1} {2} }}\,\max _{x\in [0,1]}|f_{n}(x)-f_{n-1}(x)|,\quad n\geq 1.}$

Jeżeli f oznacza funkcję graniczną, to dla każdego n ≥ 0

${\ Displaystyle \ max _ {x \ in [0,1]} | f (x) -f_ {n} (x) | \ równoważnik 2 ^ {- n + 1} \, \ max _ {x \ in [ 0,1]}|f_{1}(x)-f_{0}(x)|.}$

₀₀₀ Również wybór funkcji początkowej nie ma znaczenia, pod warunkiem, że f (0) = 0, f (1) = 1 i f jest ograniczone .

Fraktalna objętość

Funkcja Cantora jest ściśle związana ze zbiorem Cantora . Zbiór Cantora C można zdefiniować jako zbiór tych liczb z przedziału [0, 1], które nie zawierają cyfry 1 w ich rozwinięciu o podstawie 3 (triadycznej) , chyba że po 1 następują tylko zera (w którym przypadku ogon można zastąpić 0222 $aby$$\ displaystyle \ ldots},$ pozbyć się dowolnego 1). Okazuje się, że zbiór Cantora jest fraktalem z (nieprzeliczalnie) nieskończenie wieloma punktami (objętość zerowymiarowa), ale zerową długością (objętość jednowymiarowa). Tylko D $)$ objętość (w sensie miary Hausdorffa przyjmuje wartość skończoną, gdzie $displaystyle D = \log(2)/\log(3)}$ to wymiar fraktalny C . Funkcję Cantora możemy zdefiniować alternatywnie jako D -wymiarową objętość przekrojów zbioru Cantora

${\ Displaystyle f (x) = H_ {D} (C \ czapka (0, x)).}$

Samopodobieństwo

Funkcja Cantora posiada kilka symetrii . Dla ${\ Displaystyle 0 \ równoważnik x \ równoważnik 1}$ istnieje symetria odbicia

${\ Displaystyle c (x) = 1-c (1-x)}$

oraz para powiększeń, jedno po lewej, drugie po prawej:

${\ Displaystyle c \ lewo ({\ Frac {x} {3}} \ prawej) = {\ Frac {c (x)} {2}}}$

I

${\ Displaystyle c \ lewo ({\ Frac {x + 2} {3}} \ prawej) = {\ Frac {1 + c (x)} 2}}}$

Powiększenia mogą być kaskadowane; generują monoid diadyczny . Jest to pokazane przez zdefiniowanie kilku funkcji pomocniczych. Zdefiniuj odbicie jako

${\ Displaystyle r (x) = 1-x}$

Pierwszą samosymetrię można wyrazić jako

${\ Displaystyle r \ circ c = c \ circ r}$

gdzie symbol $funkcji$ . czyli ${\ Displaystyle (r \ circ c) (x) = r (c (x)) = 1-c (x)}$ i podobnie w innych przypadkach. Dla lewego i prawego powiększenia napisz lewe odwzorowania

${\ Displaystyle L_ {D} (x) = {\ Frac {x} {2}}}$ i ${\ Displaystyle L_ {C} (x) = {\frac {x}{3}}}$

Wtedy funkcja Cantora jest posłuszna

$\ circ L_ {C}}$

Podobnie zdefiniuj odpowiednie odwzorowania jako

${\ Displaystyle R_ {D} (x) = {\ Frac {1 + x} {2}}}$ i ${\ Displaystyle R_ { C}(x)={\frac {2+x}{3}}}$

Następnie, podobnie

$circ R_ {C}}$

W ten sposób obie strony mogą być lustrzanym odbiciem jednej na drugiej

${\ Displaystyle L_ {D} \ circ r = r \ circ R_ {D}}$

I podobnie,

$R_ {C}}$

Operacje te można układać dowolnie. Rozważmy na przykład sekwencję ruchów lewo-prawo ${\ displaystyle LRLLR.}$ Dodając indeksy dolne C i D oraz, dla jasności, usuwając operator kompozycji we wszystkich miejscach z wyjątkiem kilku, mamy: ${\ displaystyle \ circ }$

${\ Displaystyle L_ {D} R_ {D} L_ {D} L_ {D} R_ {D} \ circ c=c\circ L_{C}R_{C}L_{C}L_{C}R_{C}}$

Dowolne ciągi o skończonej długości w literach L i R odpowiadają diadycznym wymiernym w tym sensie, że każdy wymierny diadyczny można zapisać zarówno jako liczbę całkowitą n , jak i ${\ Displaystyle y = n/2 ^ {m}}$ m i jako skończona długość bitów ${\ Displaystyle y = 0.b_ {1} b_ {2} b_ {3} \ cdots b_ {m}}$ z ${\ Displaystyle b_ {k} \ in \ {0,1 \}.}$ Zatem każdy wymierny diadyczny jest w relacji jeden do jednego z pewną samosymetrią funkcji Cantora.

Niektóre zmiany w notacji mogą nieco ułatwić wyrażenie powyższego. Niech ${\ displaystyle g_ {1}$ i $}$ oznaczają L i R. Kompozycja funkcji rozciąga to na monoid , ponieważ można napisać ${\ displaystyle g_ {010}= g_ {0} g_ {1} g_ {0}}$ i ogólnie dla niektórych ciągów binarnych ${\ Displaystyle g_ {A} g_ {B} = g_ {AB}}$ cyfr A , B , gdzie AB jest zwykłą konkatenacją takich ciągów. Diadyczny monoid M jest zatem monoidem wszystkich takich ruchów lewo-prawo o skończonej długości. Pisząc jako ogólny element monoidu, istnieje odpowiednia samosymetria funkcji Cantora: ${\ displaystyle \ gamma \ in M}$

$\ Displaystyle \ gamma _ {D} \ circ c = c \ circ \ gamma _ {C}}$

Sam monoid diadyczny ma kilka interesujących właściwości. Można to postrzegać jako skończoną liczbę ruchów lewo-prawo w dół nieskończonego drzewa binarnego ; nieskończenie odległe „liście” na drzewie odpowiadają punktom na zbiorze Cantora, więc monoid reprezentuje również samosymetrie zbioru Cantora. W rzeczywistości duża klasa powszechnie występujących fraktali jest opisana przez monoid diadyczny; dodatkowe przykłady można znaleźć w artykule na temat krzywych de Rhama . Inne fraktale posiadające samopodobieństwo są opisywane z innymi rodzajami monoidów. Diadyczny monoid sam jest sub-monoidem grupy modularnej ${\ Displaystyle SL (2, \ mathbb {Z}).}$

Zauważ, że funkcja Cantora jest bardziej niż tylko przelotnym podobieństwem do funkcji znaku zapytania Minkowskiego . W szczególności przestrzega dokładnie tych samych relacji symetrii, chociaż w zmienionej formie.

Uogólnienia

Pozwalać

${\ Displaystyle y = \ suma _ {k = 1} ^ {\ infty} b_ {k} 2 ^ {- k}}$

będzie diadyczną (binarną) ekspansją liczby rzeczywistej 0 ≤ y ≤ 1 pod względem cyfr binarnych b _k ∈ {0,1}. Ta ekspansja jest omówiona bardziej szczegółowo w artykule na temat transformacji diadycznej . Następnie rozważ funkcję

${\ Displaystyle C_ {z} (y) = \ suma _ {k = 1} ^ {\ infty} b_ {k} z ^ {k}.}$

Dla z = 1/3 odwrotnością funkcji x = 2 C _1/3 ( y ) jest funkcja Cantora. Oznacza to, że y = y ( x ) jest funkcją Cantora. Ogólnie rzecz biorąc, dla dowolnego z < 1/2, C _z ( y ) wygląda tak, jakby funkcja Cantora była odwrócona na bok, a szerokość stopni zwiększała się, gdy z zbliża się do zera.

Jak wspomniano powyżej, funkcja Cantora jest również skumulowaną funkcją dystrybucji miary w zbiorze Cantora. Różne funkcje Cantora lub Diabelskie Schody można uzyskać, biorąc pod uwagę różne bezatomowe miary prawdopodobieństwa obsługiwane na zbiorze Cantora lub innych fraktalach. Podczas gdy funkcja Cantora prawie wszędzie ma pochodną 0, obecne badania koncentrują się na kwestii wielkości zbioru punktów, w których prawa górna pochodna różni się od prawej dolnej pochodnej, co powoduje, że pochodna nie istnieje. Ta analiza różniczkowalności jest zwykle podawana w kategoriach wymiaru fraktalnego , przy czym wymiar Hausdorffa jest najpopularniejszym wyborem. Ten kierunek badań zapoczątkował w latach 90. XX wieku Darst, który wykazał, że wymiar Hausdorffa zbioru nieróżniczkowalności funkcji Cantora jest kwadratem wymiaru zbioru Cantora ${\ Displaystyle (\ log 2 / \ log 3) ^ {2}}$ . Następnie Falconer wykazał, że ta zależność do kwadratu zachodzi dla wszystkich regularnych, pojedynczych miar Ahlfora, tj.

$${\ Displaystyle \ dim _ { H}\left\{x:f'(x)=\lim _{h\to 0^{+}}{\frac {\mu ([x,x+h])}{h}}{\text { nie istnieje}}\right\}=\left(\dim _{H}\operatorname {supp} (\mu )\right)^{2}}$$

Później Troscheit uzyskał pełniejszy obraz zbioru, w którym pochodna nie istnieje dla bardziej ogólnych znormalizowanych miar Gibba wspieranych na zbiorach samokonformalnych i samopodobnych .

Funkcja znaku zapytania Hermanna Minkowskiego luźno przypomina wizualnie funkcję Cantora, pojawiając się jako „wygładzona” forma tej ostatniej; można ją skonstruować, przechodząc od dalszego rozwinięcia ułamka do rozwinięcia binarnego, tak jak można skonstruować funkcję Cantora, przechodząc od rozwinięcia trójskładnikowego do rozwinięcia binarnego. Funkcja znaku zapytania ma interesującą właściwość posiadania znikających pochodnych dla wszystkich liczb wymiernych.

Zobacz też

• Diadyczna przemiana

Notatki

•   Bas, Richard Franklin (2013) [2011]. Prawdziwa analiza dla doktorantów (wyd. Drugie). Niezależne wydawnictwa Createspace. ISBN 978-1-4818-6914-0 .
•   Kantor G. (1884). „De la puissance des zespoły parfaits de points: Extrait d'une lettre adressée à l'éditeur” [ Moc doskonałych zestawów punktów: wyciąg z listu skierowanego do redaktora]. Acta Mathematica . International Press z Bostonu. 4 : 381–392. doi : 10.1007/bf02418423 . ISSN 0001-5962 . Przedruk w: E. Zermelo (red.), Gesammelte Abhandlungen Mathematischen und Philosophischen Inhalts, Springer, Nowy Jork, 1980.
•    Darst, Richard B.; Palagallo, Judith A.; Cena, Thomas E. (2010), Ciekawe krzywe , Hackensack, NJ: World Scientific Publishing Co. Pte. Ltd., ISBN 978-981-4291-28-6 , MR 2681574
•    Dowgoszej, O.; Martio, O.; Ryazanow, W.; Vuorinen, M. (2006). „Funkcja Cantora” . Expositiones Mathematicae . Elsevier B.V. 24 (1): 1–37. doi : 10.1016/j.exmath.2005.05.002 . ISSN 0723-0869 . MR 2195181 .
•    Fleron, Julian F. (1994-04-01). „Uwaga na temat historii zbioru Cantora i funkcji Cantora”. Magazyn Matematyczny . Informa UK Limited. 67 (2): 136–140. doi : 10.2307/2690689 . ISSN 0025-570X . JSTOR 2690689 .
• Lebesgue, H. (1904), Leçons sur l'intégration et la recherche des fonctions primitives [ Lekcje integracji i poszukiwania funkcji pierwotnych ], Paryż: Gauthier-Villars
•    Leoni, Giovanni (2017). Pierwszy kurs w przestrzeniach Sobolewa . Tom. 181 (wyd. 2). Providence, Rhode Island: Amerykańskie Towarzystwo Matematyczne. P. 734. ISBN 978-1-4704-2921-8 . OCLC 976406106 .
•   Scheeffer, Ludwik (1884). „Allgemeine Untersuchungen über Rectification der Curven” [Ogólne badania dotyczące rektyfikacji krzywych]. Acta Mathematica . International Press z Bostonu. 5 : 49–82. doi : 10.1007/bf02421552 . ISSN 0001-5962 .
•   Thomson, Brian S.; Bruckner, Judith B.; Bruckner, Andrew M. (2008) [2001]. Elementarna analiza rzeczywista (wydanie drugie). ClassicalRealAnalysis.com. ISBN 978-1-4348-4367-8 .
•   Vestrup, EM (2003). Teoria miar i integracji . Szeregi Wileya w prawdopodobieństwie i statystyce. John Wiley i synowie. ISBN 978-0471249771 .
• Vitali, A. (1905), "Sulle funzioni integrali" [O funkcjach całkowych], Atti Accad. nauka Torino Cl. nauka fis. Mata. Natura. , 40 : 1021–1034

Linki zewnętrzne

• Funkcja trójskładnikowa Cantora w Encyclopaedia of Mathematics
• Funkcja Cantora autorstwa Douglasa Riversa, projekt Wolfram Demonstrations .
• Weisstein, Eric W. „Funkcja Cantora” . MathWorld .