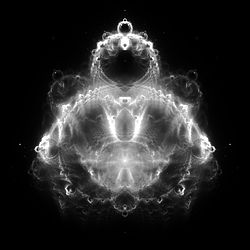
Buddabrot

Buddhabrot został powtórzony 20 000 razy.

Buddhabrot to rozkład prawdopodobieństwa na trajektoriach punktów, które wymykają się fraktalowi Mandelbrota . Jego nazwa odzwierciedla pareidoliczne podobieństwo do klasycznych przedstawień Buddy Gautamy , siedzącego w pozie medytacyjnej ze znakiem na czole ( tikka ), tradycyjnym kokiem ( ushnisha ) i lokami.

Odkrycie

Technika renderowania Buddhabrot została odkryta przez Melindę Green, która później opisała ją w poście w Usenecie z 1993 roku dla sci.fractals.

Poprzedni badacze byli bardzo bliscy znalezienia precyzyjnej techniki Buddhabrota. W 1988 roku Linas Vepstas przekazał podobne obrazy Cliffowi Pickoverowi w celu włączenia ich do mającej się wówczas ukazać książki Pickovera Computers, Pattern, Chaos, and Beauty . Doprowadziło to bezpośrednio do odkrycia łodyg Pickover . Noel Griffin również zaimplementował ten pomysł w opcji „Mandelcloud” z 1993 roku w Fractint . Jednak badacze ci nie odfiltrowali nieuciekających trajektorii wymaganych do wytworzenia upiornych form przypominających sztukę hinduską. Odwrotny filtr „Anti-Buddhabrot” tworzy obrazy podobne do braku filtrowania.

Green po raz pierwszy nazwał ten wzór Ganesh, ponieważ indyjski współpracownik „natychmiast rozpoznał go jako boga„ Ganesha ”, który ma głowę słonia”. Nazwa Buddhabrot została wymyślona później przez Lori Gardi.

Metoda renderowania

Fałszywy kolor Buddhabrot Zoom, w którym kanały czerwony, zielony i niebieski miały maksymalne wartości iteracji odpowiednio 5000, 500 i 50.

Renderowanie Buddhabrota w rozdzielczości 20 000 x 25 000 pikseli

$,$ zbiór Mandelbrota składa się ze zbioru punktów na płaszczyźnie zespolonej dla których iteracyjnie zdefiniowana sekwencja

$${\ Displaystyle z_ {n + 1} = z_ {n} ^ {2} + c}$$

nie dąży do nieskończoności $}$ gdy dąży do nieskończoności dla $\ displaystyle z_ {0} = 0$ { .

Fałszywy kolor Buddhabrot, w którym kanały czerwony, zielony i niebieski miały maksymalne wartości iteracji odpowiednio 5000, 500 i 50.

Obraz Buddhabrot można zbudować, najpierw tworząc dwuwymiarową tablicę pudełek , z których każda odpowiada ostatniemu pikselowi obrazu. Każde pudełko ${\ Displaystyle (i, j)}$ dla ${\ Displaystyle i = 1, \ ldots, m}$ i ${\ Displaystyle j = 1 , \ ldots, n}$ ma rozmiar we współrzędnych zespolonych ${\ Displaystyle \ Delta x}$ i ${\ Displaystyle \ Delta y}$ , gdzie ${\ Displaystyle \ Delta x = w/m}$ i $Displaystyle \ Delta y = h/n}$$\ displaystyle h}$ dla obrazu o szerokości i wysokości $w$ . Dla każdego pola odpowiedni licznik jest inicjalizowany na zero. Następnie losowe próbkowanie $jest$ iterowane przez funkcję Mandelbrota. Dla punktów, które uciekają w wybranej maksymalnej liczbie iteracji, a zatem nie znajdują się w zbiorze Mandelbrota, licznik dla każdego pola wprowadzonego podczas ucieczki do nieskończoności jest zwiększany o 1. Innymi słowy, dla każdej sekwencji odpowiadającej ${\ displaystyle c}$ , który ucieka, dla każdego punktu ${\ Displaystyle ({\ tekst {Re$ ucieczki, pole, które $n$ leży w obrębie zwiększa się o 1. Punkty, które nie uciekają w ciągu maksymalnej liczby iteracji (i uważane za należące do zbioru Mandelbrota) są odrzucane. Po powtórzeniu dużej liczby $są$ odcienie szarości następnie wybierane na podstawie rozkładu wartości zapisanych w tablicy. Rezultatem jest wykres gęstości podkreślający regiony, w których $wartości$ czasu na drodze do nieskończoności.

Antybuddhabrot

Buddhabrot wraz ze wzrostem maksymalnej liczby iteracji

Niuanse

Renderowanie obrazów Buddhabrota jest zwykle bardziej wymagające obliczeniowo niż standardowe techniki renderowania Mandelbrota. Wynika to częściowo z konieczności iteracji większej liczby przypadkowych punktów niż pikseli w obrazie w celu uzyskania ostrego obrazu. Renderowanie bardzo powiększonych obszarów wymaga jeszcze więcej obliczeń niż w przypadku standardowych obrazów Mandelbrota, w których dany piksel można obliczyć bezpośrednio, niezależnie od poziomu powiększenia. I odwrotnie, na piksel w powiększonym regionie obrazu Buddhabrot mogą wpływać początkowe punkty z obszarów daleko poza renderowanym. Bez uciekania się do bardziej złożonych technik probabilistycznych renderowanie powiększonych części Buddhabrot polega jedynie na przycięciu dużego, pełnowymiarowego renderowania.

Maksymalna wybrana liczba iteracji wpływa na obraz – wyższe wartości dają mniej szczegółowy wygląd, ponieważ kilka punktów przechodzi przez dużą liczbę pikseli, zanim uciekną, co powoduje, że ich ścieżki są bardziej widoczne. Gdyby zastosowano niższe maksimum, punkty te nie uciekłyby w czasie i zostałyby uznane za nieuciekające w ogóle. Liczba wybranych próbek wpływa również na obraz, ponieważ większa liczba próbek nie tylko zmniejsza szum obrazu, ale może zmniejszyć widoczność wolno poruszających się punktów i małych atraktorów, które mogą pojawić się jako widoczne smugi w renderowaniu mniejszej liczby próbek . Niektóre z tych smug są widoczne na poniższym obrazie z 1 000 000 iteracji.

Green później zdał sobie sprawę, że zapewniło to naturalny sposób tworzenia kolorowych obrazów Buddhabrot poprzez wykonanie trzech takich obrazów w skali szarości , różniących się jedynie maksymalną liczbą użytych iteracji, i połączenie ich w jeden kolorowy obraz przy użyciu tej samej metody, której używali astronomowie do tworzenia fałszywych kolorów obrazy mgławic i innych ciał niebieskich. Na przykład można przypisać obraz o maksymalnej iteracji 2000 do kanału czerwonego, obraz o maksymalnej iteracji 200 do kanału zielonego i obraz o maksymalnej iteracji 20 do kanału niebieskiego obrazu w przestrzeni kolorów RGB . Niektórzy oznaczyli obrazy Buddhabrot przy użyciu tej techniki Nebulabrots .

Maksymalna liczba iteracji: 20

Maksymalna liczba iteracji: 100

Maksymalna liczba iteracji: 1000

Maksymalna liczba iteracji: 20 000

Maksymalna liczba iteracji: 1 000 000

Związek z mapą logistyczną

Buddhabrot i jego mapa logistyczna.

Animacja przedstawiająca Buddhabrota i jego mapę logistyczną.

Związek między zbiorem Mandelbrota $x (1-x)$ przez iterację a mapą logistyczną $x )$ jest dobrze znany. Oba są powiązane przez transformację kwadratową:

$${\ Displaystyle {\ rozpocząć {wyrównane} c_ {r} i = {\ Frac {\ lambda ( 2-\lambda )}{4}}\\c_{i}&=0\\z_{r}&=-{\frac {\lambda (2x-1)}{2}}\\z_{i} &=0\end{wyrównane}}}$$

Tradycyjnym sposobem zilustrowania tej zależności jest wyrównanie mapy logistycznej i zestawu Mandelbrota za pomocą relacji między i , przy użyciu wspólnej osi x i innej osi y- $c_ {r$ { $}}$ osi, pokazując jednowymiarową zależność.

Melinda Green odkryła „przez przypadek”, że paradygmat anty-Buddhabrot w pełni integruje mapę logistyczną. Oba oparte są na śledzeniu ścieżek z punktów nieuciekających, iterowanych z (losowego) punktu początkowego, a funkcje iteracyjne są powiązane przez transformację podaną powyżej. Łatwo wtedy zauważyć, że Anti-Buddhabrot dla $z$ c $,$$Displaystyle c = ({\ tekst {losowo}$ z ${\ Displaystyle Z_ {0} = (0,0)} po$ generuje mapę logistyczną na płaszczyźnie $Displaystyle \ {c_ {r}, z_{r}\}}$ , przy użyciu podanej transformacji. Do celów renderowania używamy ${\ displaystyle z_ {0} = ({\ text {losowo}}, 0)}$ . Na mapie logistycznej wszystkie $.$ tę samą ścieżkę

Ponieważ zarówno zestaw Mandelbrota, jak i mapa logistyczna są integralną częścią Anty-Buddhabrota, możemy teraz pokazać trójwymiarową relację między nimi, używając osi 3D { $\ Displaystyle \ {c_ {r },c_{i},z_{r}\}}$ . Animacja przedstawia klasycznego Anti-Buddhabrota z ${\ Displaystyle c = ({\ tekst {losowo}}, {\ tekst {losowo}})}$ i ${\ Displaystyle z_ { 0} = (0,0)}$ , to jest zestaw 2D Mandelbrota na płaszczyźnie ${\ Displaystyle \ {c_ {r}, c_ {i} \}}$ , a także anty-Buddhabrot gdzie do ${\ Displaystyle c = ({\ tekst {losowo}}, 0)}$ i ${\ Displaystyle z_ {0} = (0,0)} , to$ logistyka 2D mapa w płaszczyźnie ${\ Displaystyle \ {c_ {r}, z_ {r} \}}$ . Obracamy płaszczyznę wokół ${\ Displaystyle \ {c_ {r}, c_ {i} \}}$$,$$\ displaystyle c_ {$ najpierw , a następnie obracając o 90 °, aby pokazać $\ Displaystyle \ {c_ {r}, z_ {r} \}}$ , a następnie obracając dodatkowe 90 °, aby pokazać $\ Displaystyle \ {c_ {r}, -c_ {i} \}}$ . Moglibyśmy obrócić dodatkowe 180 °, ale daje to te same obrazy, odbite lustrzanie wokół ${\ displaystyle c_ {r}}$ .

$płaszczyźnie$ podzbiorem klasycznego Anti-Buddhabrota, ${\ Displaystyle c_ {i} = 0}$ lub ) 3D ${\ Displaystyle \ {c_ {r}, c_ {i}, z_ {r} \}}$ prostopadle do płaszczyzna ${\ Displaystyle \ {c_ {r}, c_ {i} \}}$ . Podkreślamy to, pokazując krótko, przy obrocie o 90 °, tylko rzutowaną płaszczyznę, $„$ zakłóconą” przez rzuty płaszczyzn o niezerowym do $displaystyle c_ {i}}$ .

Linki zewnętrzne

• Łobo, Albert. „Poznaj technikę Buddhabrot” . Gęstość cząsteczkowa . Zarchiwizowane od oryginału w dniu 03.09.2018 . Źródło 2011-11-21 .
• matematyk. „Ciemna strona zbioru Mandelbrota” . YouTube . Zarchiwizowane od oryginału w dniu 2021-12-22.