Punkt Misiurewicza

Orbita przedokresowa

W matematyce punkt Misiurewicza jest wartością parametru w zbiorze Mandelbrota ( przestrzeń parametrów zespolonych odwzorowań kwadratowych), a także w rzeczywistych odwzorowaniach kwadratowych przedziału, dla którego punkt krytyczny jest ściśle przedokresowy (tj. staje się okresowy po skończonej liczbie iteracji ale sam nie jest okresowy). Przez analogię termin punkt Misiurewicza jest również używany dla parametrów w zbiorze multibrotowym gdzie unikalny punkt krytyczny jest ściśle przedokresowy. (Ten termin ma mniej sensu w przypadku map, które mają więcej niż jeden (wolny) punkt krytyczny, ponieważ niektóre punkty krytyczne mogą być okresowe, a inne nie). Punkty te zostały nazwane na cześć matematyka Michała Misiurewicza , który jako pierwszy je badał.

Główny Misiurewicz punkt stypy 1/31

Notacja matematyczna

Parametr jest punktem Misiurewicza $M_ {k, n}},$$k$ spełnia równania

${\ Displaystyle f_ {c} ^ {(k)} (z_ {cr}) = f_ {c} ^ {( k+n)}(z_{cr})}$

I

${\ Displaystyle f_ {c} ^ {(k-1)} (z_ {cr}) \ neq f_{c}^{(k+n-1)}(z_{cr})}$

Więc :

${\ Displaystyle M_ {k, n} = c: f_ {c} ^ {(k )}(z_{cr})=f_{c}^{(k+n)}(z_{cr})}$

Gdzie :

• ${\ displaystyle z_ {cr}}$ jest punktem krytycznym ${\ displaystyle f_ {c}$ do ,
• ${\ displaystyle k}$ i ${\ displaystyle n}$ są dodatnimi liczbami całkowitymi,
• $(k)}}$${\ displaystyle k}$ oznacza -ty iterację ${\ displaystyle f_ {c}}$ .

Nazwa

Punkty Misiurewicza zostały nazwane na cześć polsko-amerykańskiego matematyka Michała Misiurewicza .

Termin „punkt Misiurewicza” jest używany niejednoznacznie: Misiurewicz pierwotnie badał mapy, w których wszystkie punkty krytyczne były jednorazowe (to znaczy istnieje sąsiedztwo każdego punktu krytycznego, którego nie odwiedza orbita tego punktu krytycznego), i to znaczenie jest mocno ugruntowane w kontekście dynamiki iterowanych map interwałowych. Przypadek, w którym dla wielomianu kwadratowego unikalny punkt krytyczny jest ściśle przedokresowy, jest tylko bardzo szczególnym przypadkiem. W tym ograniczonym znaczeniu termin ten jest używany w złożonej dynamice; bardziej odpowiednie byłyby punkty Misiurewicza-Thurstona (za Williamem Thurstonem , który badał postkrytycznie skończone mapy wymierne).

Mapy kwadratowe

Złożony wielomian kwadratowy ma tylko jeden punkt krytyczny. $Za$ odpowiedniej koniugacji postaci jeden wskaż na ${\ displaystyle z = 0}$ . Punkty Misiurewicza tej rodziny map są pierwiastkami równań

${\ Displaystyle P_ {c} ^ {(k)} (0) = P_ {c} ^ {(k + n)} (0) ,}$

(pod warunkiem, że punkt krytyczny nie jest okresowy), gdzie:

• k to przedokres
• n to okres
• ${\ Displaystyle P_ {c} ^ {(n)} = P_ {c} (P_ {c} ^ {(n-1)})}$ oznacza n -krotną kompozycję ${\ Displaystyle P_ {c} (z) = z ^ {2} + c}$ do , tj. n ^-tą iteracją do ${\ displaystyle P_ {c}}$ .

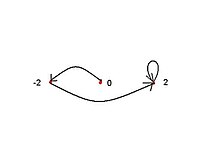
Na przykład punkty Misiurewicza o k =2 i n =1, oznaczane przez M _2,1 , są pierwiastkami

${\ Displaystyle {\ rozpocząć {wyrównane} i P_ {c}^{(2)}(0)=P_{c}^{(3)}(0)\\\strzałka w prawo {}&c^{2}+c=(c^{2}+c)^ {2}+c\\\Strzałka w prawo {}&c^{4}+2c^{3}=0.\end{aligned}}}$

Pierwiastek c = 0 nie jest punktem Misiurewicza, ponieważ punkt krytyczny jest punktem stałym, gdy c = 0, a więc jest raczej okresowy niż przedokresowy. Pozostawia to pojedynczy punkt Misiurewicza M _2,1 w c = −2.

Własności punktów Misiurewicza złożonego odwzorowania kwadratowego

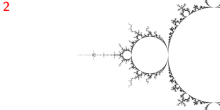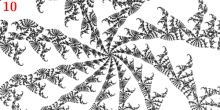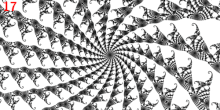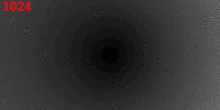
Punkty Misiurewicza należą do granicy zbioru Mandelbrota . Punkty Misiurewicza są gęste na granicy zbioru Mandelbrota.

Jeśli jest punktem $Misiurewicza$ , to powiązany wypełniony zbiór Julii jest równy zbiorowi Julii i oznacza że ​​wypełniony zbiór Julii nie ma wnętrza .

Jeśli jest punktem $Misiurewicza$ , to w odpowiednim zbiorze Julii wszystkie cykle okresowe odpychają się (w szczególności cykl, na który przypada orbita krytyczna)

$są$ Mandelbrota i zbiór Julii lokalnie asymptotycznie samopodobne wokół punktów Misiurewicza

typy

Kryteria klasyfikacji:

• liczbę padających na nie promieni zewnętrznych
• typy wizualne

Punkty Misiurewicza można podzielić ze względu na liczbę padających na nie promieni zewnętrznych

• z 3 lub więcej argumentami zewnętrznymi (lub kątami) , punktami rozgałęzień, które rozłączają zbiór Mandelbrota,
• z dokładnie 2 argumentami zewnętrznymi (punkty łuków w zbiorze Mandelbrota), które są mniej rzucające się w oczy i niełatwo je znaleźć na obrazach; punkty nierozgałęzione
• z 1 zewnętrznym argumentem: końcówki gałęzi = punkty końcowe

Typy wizualne

• wskazówki dotyczące gałęzi
• centra spirali
• punkty, w których spotykają się gałęzie

Zgodnie z Twierdzeniem o gałęziach zbioru Mandelbrota wszystkie punkty rozgałęzień zbioru Mandelbrota są punktami Misiurewicza.

Większość parametrów Misiurewicza w zbiorze Mandelbrota wygląda jak „środki spiral”. Wyjaśnieniem tego jest to, że przy parametrze Misiurewicza wartość krytyczna przeskakuje do odpychającego cyklu okresowego po skończonej liczbie iteracji. W każdym punkcie cyklu zbiór Julii jest asymptotycznie samopodobny dzięki złożonemu mnożeniu przez pochodną tego cyklu. Jeśli pochodna jest nierzeczywista, oznacza to, że zestaw Julii w pobliżu cyklu okresowego ma strukturę spiralną. Tak więc podobna struktura spiralna występuje w zestawie Julii w pobliżu wartości krytycznej i według Tan Lei twierdzenie, także w zbiorze Mandelbrota w pobliżu dowolnego parametru Misiurewicza, dla którego orbita odpychająca ma nierzeczywisty mnożnik. W zależności od wartości tego mnożnika kształt spirali może wydawać się mniej lub bardziej wyraźny. Liczba ramion spirali jest równa liczbie rozgałęzień przy parametrze Misiurewicza, a to jest równe liczbie rozgałęzień przy wartości krytycznej w zbiorze Julii. Nawet główny punkt Misiurewicza w ramieniu 1/3, na końcu promieni parametrycznych pod kątami 9/56, 11/56 i 15/56, okazuje się asymptotycznie spiralą o nieskończenie wielu zwojach, mimo że ciężko to zobaczyć bez powiększenia.

Argumenty zewnętrzne

Zewnętrzne argumenty punktów Misiurewicza, mierzone kolejno , to:

• liczby wymierne
• ułamek właściwy z parzystym mianownikiem
  • ułamki diadyczne ${\ displaystyle = 2 ^ {b} }$ mianownikiem i skończonym ( zakończonym ) rozwinięciem:
    $${\ Displaystyle {\ Frac {1} {2}} _ {10} = 0,5_ {10} = 0,1_ {2}}$$
  • ułamek z mianownikiem ${\ Displaystyle = a \ cdot 2 ^ {b}}$ i powtarzającym się rozwinięciem :
    $${\ Displaystyle {\ Frac {1} {6}} _ {10} = {\ Frac {1} {2 \ razy 3}} _ {10} = 0,16666... ​​_ {10} = 0,0 (01). .._{2}.}$$

gdzie: aib są liczbami całkowitymi dodatnimi, a b jest liczbą nieparzystą, liczba w indeksie dolnym oznacza podstawę systemu liczbowego .

Przykłady punktów Misiurewicza złożonego odwzorowania kwadratowego

Punkty końcowe

Orbita punktu krytycznego ${\ Displaystyle Z = 0}$ poniżej ${\ Displaystyle f_ {- 2}}$

${\ Displaystyle c = M_ {2,1}}$

Punkt ${\ Displaystyle c = M_ {2,2} = i}$ :

• jest końcówką filamentu
• punkt lądowania promienia zewnętrznego dla kąta = 1/6
• Jego orbity krytyczne to ${\ Displaystyle \ {0, ja, i-1, -i, i-1, -i... \}}$

punkt ${\ Displaystyle c = M_ {2,1} = -2}$

• jest punktem końcowym anteny głównej zbioru Mandelbrota
• jest punktem lądowania tylko jednego promienia zewnętrznego (promienia parametrycznego) o kącie 1/2
• Jego orbita krytyczna:
  • jest ${\ Displaystyle \ {0, -2,2,2,2,... \}}$
  • Sekwencja symboliczna = CLRRR ...
  • przedokres to 2, a okres 1

Punkty oddziałów

Powiększ główny punkt Misiurewicza dla okresów od 2 do 1024

${\ Displaystyle c = M_ {4,1}}$

Punkt ${\ Displaystyle c = -0,10109636384562... + i \, 0,95628651080914... = M_ {4,1}}$

• jest głównym punktem Misiurewicza kończyny 1/3
• ma 3 promienie zewnętrzne : 9/56, 11/56 i 15/56.

Inne punkty

Są to punkty, które nie są punktami rozgałęzionymi i niekońcowymi.

${\ Displaystyle c = M_ {23,2}}$

Punkt ${\ Displaystyle c = -0,77568377 + i \, 0,13646737}$ znajduje się w pobliżu punktu Misiurewicza ${\ Displaystyle M_ {23,2}}$ . To jest

• środek dwuramiennej spirali
• punkt lądowania 2 promieni zewnętrznych z kątami: ${\ displayStyle {\ frac {8388611} {25165824}}}$ i ${\ displayStyle {\ frac {8388613}}$ Ator to ${\ Displaystyle 3 * 2 ^ {23}}$
• punkt przedokresowy z przedokresem $}$$displaystyle$ {

Punkt ${\ Displaystyle c = -1,54368901269109}$ znajduje się w pobliżu punktu Misiurewicza $}$ }

• który jest punktem lądowania pary promieni: ${\ Displaystyle {\ Frac {5} {12}}}$ , ${\ Displaystyle {\ Frac {7} {12}}}$
• ma przedokres i ${\ displaystyle k = 3}$ i okres ${\ displaystyle n = 1}$

Zobacz też

• Dynamika arytmetyczna
• Punkt Feigenbauma
• Dendryt (matematyka)

Dalsza lektura

• Michał Misiurewicz (1981), "Miary bezwzględnie ciągłe dla pewnych map interwału" . Publikacje Mathématiques de l'IHÉS, 53 (1981), s. 17-51

Linki zewnętrzne

• Punkty przedokresowe (Misiurewicz) w zestawie Mandelbrota Jewgienija Demidowa
• Podobieństwo zestawów M i J dla punktów przedokresowych. Twierdzenie Lei autorstwa Douglasa C. Ravenela
• Misiurewicz Punkt mapy logistycznej JC Sprott