Mapa logistyczna

Mapa logistyczna to odwzorowanie wielomianowe (równoważne relacji powtarzalności ) stopnia 2 , często określane jako archetypowy przykład tego, jak złożone, chaotyczne zachowanie może wynikać z bardzo prostych nieliniowych równań dynamicznych. Mapa została spopularyzowana w artykule z 1976 roku przez biologa Roberta Maya , częściowo jako model demograficzny w czasie dyskretnym, analogiczny do równania logistycznego zapisanego przez Pierre'a François Verhulsta . Z matematycznego punktu widzenia mapa logistyczna jest napisana

${\ Displaystyle x_ {n + 1} = rx_ {n} (1-x_ {n}),}$

 

 

 

 

()

gdzie x _n jest liczbą z przedziału od zera do jeden, która reprezentuje stosunek istniejącej populacji do maksymalnej możliwej liczby ludności. To nieliniowe równanie różnicowe ma na celu uchwycenie dwóch efektów:

• reprodukcja , gdzie populacja będzie rosła w tempie proporcjonalnym do obecnej populacji, gdy liczebność populacji jest mała,
• głód (śmiertelność zależna od gęstości), gdzie tempo wzrostu będzie spadać w tempie proporcjonalnym do wartości uzyskanej przez odjęcie teoretycznej „nośności” środowiska pomniejszonej o obecną populację.

Zwykłe interesujące nas wartości parametru r mieszczą się w przedziale [0, 4] , tak że x _n pozostaje ograniczone przez [0, 1] . Przypadek r = 4 mapy logistycznej jest nieliniową transformacją zarówno mapy z przesunięciem bitowym , jak i przypadku μ = 2 mapy namiotu . Jeśli r > 4 , prowadzi to do ujemnych wielkości populacji. (Ten problem nie występuje w starszym modelu Rickera , co również wykazuje chaotyczną dynamikę.) Można również rozważyć wartości r w przedziale [−2, 0] , tak że x _n pozostaje ograniczone przez [−0,5, 1,5] .

Charakterystyka mapy

Zachowanie zależne od r

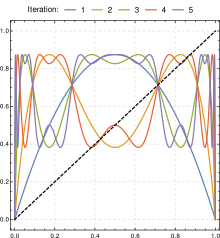
Poniższy obraz przedstawia zawartość amplitudy i częstotliwości niektórych iteracji mapy logistycznej dla wartości parametrów z zakresu od 2 do 4.

Zmieniając parametr r obserwuje się następujące zachowanie:

Ewolucja różnych warunków początkowych w funkcji r

• Przy r między 0 a 1 populacja ostatecznie umrze, niezależnie od populacji początkowej.
• Przy r między 1 a 2 populacja szybko zbliży się do wartości r - 1 / r , niezależnie od populacji początkowej.
• 

  Ewolucja różnych warunków początkowych jako funkcja r z obciążeniem
  Gdy r wynosi od 2 do 3, populacja również ostatecznie zbliży się do tej samej wartości r - 1 / r , ale najpierw przez pewien czas będzie oscylować wokół tej wartości. Szybkość konwergencji jest liniowa, z wyjątkiem r = 3 , kiedy jest dramatycznie powolna, mniej niż liniowa (patrz Pamięć bifurkacji ).
• Przy r między 3 a 1 + √ 6 ≈ 3,44949 populacja zbliży się do stałych oscylacji między dwiema wartościami. Te dwie wartości są zależne od r i podane przez ${\ Displaystyle x_ {\ pm} = {\ Frac {1} {2r} }\left(r+1\pm {\sqrt {(r-3)(r+1)}}\right)}$ .
• Przy r między 3,44949 a 3,54409 (w przybliżeniu), z prawie wszystkich warunków początkowych populacja zbliży się do stałych oscylacji między czterema wartościami. Ta ostatnia liczba jest pierwiastkiem wielomianu 12 stopnia (sekwencja A086181 w OEIS ).
• Gdy r wzrośnie powyżej 3,54409, z prawie wszystkich warunków początkowych populacja zbliży się do oscylacji między 8 wartościami, następnie 16, 32 itd. Długości przedziałów parametrów, które dają oscylacje o danej długości, szybko się zmniejszają; stosunek długości dwóch kolejnych przedziałów bifurkacji zbliża się do stałej Feigenbauma δ ≈ 4,66920 . To zachowanie jest przykładem kaskady podwajania okresu .
• Przy r ≈ 3,56995 (sekwencja A098587 w OEIS ) jest początkiem chaosu, na końcu kaskady podwojenia okresu. Z prawie wszystkich warunków początkowych nie widzimy już oscylacji o skończonym okresie. Niewielkie różnice w początkowej populacji dają dramatycznie różne wyniki w czasie, co jest podstawową cechą chaosu.
• Większość wartości r powyżej 3,56995 wykazuje zachowanie chaotyczne, ale nadal istnieją pewne izolowane zakresy r , które wykazują zachowanie niechaotyczne; są one czasami nazywane wyspami stabilności . Na przykład, począwszy od 1 + √ 8 (w przybliżeniu 3,82843) istnieje zakres parametrów r , które pokazują oscylację między trzema wartościami, a dla nieco wyższych wartości oscylacji r między 6 wartościami, a następnie 12 itd.
• Rozwój chaotycznego zachowania sekwencji logistycznej, gdy parametr r zmienia się od około 3,56995 do około 3,82843, jest czasami nazywany scenariuszem Pomeau – Manneville'a , charakteryzującym się okresową (laminarną) fazą przerywaną wybuchami aperiodycznego zachowania. Taki scenariusz ma zastosowanie w urządzeniach półprzewodnikowych. Istnieją inne zakresy, które dają oscylację między 5 wartościami itp.; wszystkie okresy oscylacji występują dla pewnych wartości r . Okno podwojenia okresu z parametrem c jest zakresem r -wartości składające się z kolejnych podzakresów. K - ty podzakres zawiera wartości r , dla których istnieje stały cykl (cykl przyciągający zbiór początkowych punktów o jednostkowej mierze) o okresie 2 ^k c . Ta sekwencja podzakresów nazywana jest kaskadą harmonicznych . W podzakresie ze stabilnym cyklem o okresie 2 ^{k *} c występują niestabilne cykle o okresie 2 ^k c dla wszystkich k < k * . r _ wartość na końcu nieskończonego ciągu podzakresów nazywana jest punktem spiętrzenia kaskady harmonicznych. Wraz ze r pojawia się szereg nowych okien o różnych wartościach c . Pierwszy dotyczy c = 1 ; wszystkie kolejne okna obejmujące nieparzyste c występują w porządku malejącym c , zaczynając od dowolnie dużego c .
• Powyżej r = 4 prawie wszystkie wartości początkowe ostatecznie opuszczają przedział [0,1] i rozchodzą się. Zbiór warunków początkowych, które mieszczą się w [0,1], tworzy zbiór Cantora , a dynamika ograniczona do tego zbioru Cantora jest chaotyczna.

Dla dowolnej wartości r istnieje co najwyżej jeden stabilny cykl. Jeśli istnieje stabilny cykl, jest on globalnie stabilny i przyciąga prawie wszystkie punkty. Niektóre wartości r ze stabilnym cyklem pewnego okresu mają nieskończenie wiele niestabilnych cykli różnych okresów.

Schemat bifurkacji po prawej podsumowuje to. Oś pozioma pokazuje możliwe wartości parametru r , podczas gdy oś pionowa pokazuje zbiór wartości x odwiedzanych asymptotycznie z prawie wszystkich warunków początkowych przez iteracje równania logistycznego z tą wartością r .

Schemat bifurkacji dla mapy logistycznej. Atraktor dla dowolnej wartości parametru r jest pokazany na linii pionowej w tym r .

Diagram bifurkacji jest samopodobny : jeśli powiększymy wspomnianą powyżej wartość r ≈ 3,82843 i skupimy się na jednym ramieniu z trzech, sytuacja w pobliżu wygląda jak zmniejszona i nieco zniekształcona wersja całego diagramu. To samo dotyczy wszystkich innych niechaotycznych punktów. Jest to przykład głębokiego i wszechobecnego związku między chaosem a fraktalami .

Powiększenie chaotycznego regionu mapy.

Stabilne regiony w regionie chaotycznym, gdzie styczna bifurkacja występuje na granicy między atraktorem chaotycznym i okresowym, dając przerywane trajektorie, jak opisano w scenariuszu Pomeau – Manneville .

Możemy również rozważyć ujemne wartości r :

• Dla r między -2 a -1 sekwencja logistyczna również charakteryzuje się zachowaniem chaotycznym.
• ₀ Przy r między -1 a 1 - √ 6 i dla x między 1/ r a 1-1/ r , populacja zbliży się do stałych oscylacji między dwiema wartościami, jak w przypadku r między 3 a 1 + √ 6 , i biorąc pod uwagę według tej samej formuły.

Chaos i mapa logistyczna

Schemat pajęczyny mapy logistycznej, przedstawiający chaotyczne zachowanie dla większości wartości r > 3,57

Funkcja logistyczna f (niebieska) i jej iterowane wersje f ² , f ³ , f ⁴ i f ⁵ dla r = 3,5 . Na przykład dla dowolnej wartości początkowej na osi poziomej f ⁴ daje wartość iteracji cztery iteracje później.

Względna prostota mapy logistycznej sprawia, że ​​jest ona szeroko stosowanym punktem wyjścia do rozważań nad pojęciem chaosu. Zgrubny opis chaosu jest taki, że systemy chaotyczne wykazują dużą wrażliwość na warunki początkowe — właściwość mapy logistycznej dla większości wartości r między około 3,57 a 4 (jak wspomniano powyżej). Częstym źródłem takiej wrażliwości na warunki początkowe jest to, że mapa przedstawia powtarzające się składanie i rozciąganie przestrzeni, na której jest zdefiniowana. W przypadku mapy logistycznej równanie różnicowe kwadratowe opisując to można traktować jako operację rozciągania i składania na przedziale (0,1) .

Poniższy rysunek ilustruje rozciąganie i składanie sekwencji iteracji mapy. Rysunek (a) po lewej pokazuje dwuwymiarowy wykres Poincarégo przestrzeni stanów mapy logistycznej dla r = 4 i wyraźnie pokazuje krzywą kwadratową równania różnicowego ( 1 ). Możemy jednak osadzić tę samą sekwencję w trójwymiarowej przestrzeni stanów, aby zbadać głębszą strukturę mapy. Rysunek (b) po prawej pokazuje to, pokazując, jak początkowo pobliskie punkty zaczynają się rozchodzić, szczególnie w tych obszarach x _t odpowiadające bardziej stromym częściom działki.

To rozciąganie i składanie nie tylko powoduje stopniową rozbieżność sekwencji iteracji, ale także rozbieżność wykładniczą (patrz wykładniki Lapunowa ), o czym świadczy również złożoność i nieprzewidywalność chaotycznej mapy logistycznej. W rzeczywistości rozbieżność wykładnicza sekwencji iteracji wyjaśnia związek między chaosem a nieprzewidywalnością: mały błąd w przypuszczalnym stanie początkowym systemu będzie odpowiadał dużemu błędowi w późniejszej fazie jego ewolucji. W związku z tym przewidywania dotyczące przyszłych stanów stają się stopniowo (a właściwie wykładniczo) . ) gorzej, gdy są nawet bardzo małe błędy w naszej wiedzy o stanie początkowym. Ta cecha nieprzewidywalności i pozornej przypadkowości doprowadziła do wykorzystania równania mapy logistycznej jako generatora liczb pseudolosowych we wczesnych komputerach.

Ponieważ mapa jest ograniczona do przedziału na osi liczb rzeczywistych, jej wymiar jest mniejszy lub równy jedności. Szacunki numeryczne dają wymiar korelacji 0,500 ± 0,005 ( Grassberger , 1983), wymiar Hausdorffa około 0,538 ( Grassberger 1981) i wymiar informacyjny około 0,5170976 ( Grassberger 1983) dla r ≈ 3,5699456 (początek chaosu). Uwaga: Można wykazać, że wymiar korelacji mieści się z pewnością w przedziale od 0,4926 do 0,5024.

Często jednak możliwe jest sformułowanie precyzyjnych i dokładnych stwierdzeń o prawdopodobieństwie przyszłego stanu w systemie chaotycznym. Jeśli (prawdopodobnie chaotyczny) system dynamiczny ma atraktor , to istnieje miara prawdopodobieństwa , która określa długoterminową proporcję czasu spędzonego przez system w różnych obszarach atraktora. W przypadku mapy logistycznej o parametrze r = 4 i stanie początkowym w (0,1) atraktorem jest również przedział (0,1) a miara prawdopodobieństwa odpowiada rozkład beta z parametrami a = 0,5 i b = 0,5 . W szczególności niezmienną miarą jest

${\ Displaystyle {\ Frac {1} {\ pi {\ sqrt {x (1-x)}}}}.}$

Nieprzewidywalność nie jest przypadkowością, ale w niektórych okolicznościach bardzo ją przypomina. Dlatego na szczęście, nawet jeśli wiemy bardzo mało o początkowym stanie mapy logistycznej (lub innego chaotycznego systemu), wciąż możemy powiedzieć coś o rozmieszczeniu stanów w arbitralnie odległej przyszłości i wykorzystać tę wiedzę do podejmowania decyzji na podstawie stanu systemu.

Reprezentacja graficzna

Diagram bifurkacji dla mapy logistycznej można zwizualizować za pomocą następującego kodu Pythona :

   
   

     
  
    
  
  

   
 import  numpy  jako  np  import  matplotlib.pyplot  jako  plt  interwał  =  (  2.8  ,  4  )  # początek, koniec  dokładność  =  0,0001  powtórzeń  =  600  # liczba powtórzeń  numtoplot  =  200  lims  =  np  .  zera  (  powtórzenia  )  rys.  ,  biax  =  plt  .  podploty  ()  ryc  

0  
   0  
       
         .  set_size_inches  (  16  ,  9  )  lims  [  ]  =  np  .  losowy  .  rand  ()  dla  r  w  np  .  arange  (  interwał  [  ],  interwał  [  1  ],  dokładność  ):  dla  i  w  zakresie  (  powtórzeń  -  1  ):  lims  [  i  +  1  ]   

       

  =  r  *  lims  [  ja  ]  *  (  1  -  lims  [  ja  ])  biax  .  plot  ([  r  ]  *  numtoplot  ,  lims  [  reps  -  numtoplot  :],  'b.'  ,  markersize  =  0,02  )  biax  .  zestaw  (  xlabel  =  'r'  ,  ylabel  =  
 'x'  ,  title  =  'mapa logistyczna'  )  plt  .  pokaż  () 

Specjalne przypadki mapy

Górna granica, gdy 0 ≤ r ≤ 1

Chociaż dokładne rozwiązania relacji powtarzalności są dostępne tylko w niewielkiej liczbie przypadków, górna granica mapy logistycznej w postaci zamkniętej jest znana, gdy 0 ≤ r ≤ 1 . Istnieją dwa aspekty zachowania mapy logistycznej, które powinny być uchwycone przez górną granicę w tym reżimie: asymptotyczny zanik geometryczny ze stałą r i szybki początkowy zanik, gdy x ₀ jest bliski 1, napędzany przez (1 - x _n ) wyraz w relacji rekurencyjnej. Poniższa granica obejmuje oba te efekty:

${\ Displaystyle \ forall n \ in \ {0,1, \ ldots \} \ quad {\ tekst {i}} \ quad x_ {0}, r \ in [0,1], \ quad x_ {n} \ leq {\frac {x_{0}}{r^{-n}+x_{0}n}}.}$

Rozwiązanie, gdy r = 4

Szczególny przypadek r = 4 można w rzeczywistości rozwiązać dokładnie, podobnie jak przypadek r = 2 ; jednak ogólny przypadek można przewidzieć tylko statystycznie. Rozwiązaniem, gdy r = 4 jest,

${\ Displaystyle x_ {n} = \ sin ^ {2} \ lewo (2 ^ {n} \ teta \ pi \ po prawej)}$

gdzie parametr warunku początkowego θ jest określony przez

${\ Displaystyle \ theta = {\ tfrac {1} {\ pi}} \ sin ^ {-1} \ lewo ({\ sqrt {x_ {0}}} \ prawej).}$

Dla wymiernego θ , po skończonej liczbie iteracji x _n odwzorowuje się na sekwencję okresową. Ale prawie wszystkie θ są irracjonalne , a dla irracjonalnego θ xn nigdy się _nie powtarza – jest nieokresowe. To równanie rozwiązania wyraźnie pokazuje dwie kluczowe cechy chaosu – rozciąganie i składanie: współczynnik 2 ⁿ pokazuje wykładniczy wzrost rozciągania, co skutkuje wrażliwą zależnością od warunków początkowych , podczas gdy kwadrat funkcji sinus zachowuje x _n złożony w zakresie [0,1] .

Dla r = 4 równoważne rozwiązanie pod względem liczb zespolonych zamiast funkcji trygonometrycznych jest

${\ Displaystyle x_ {n} = {\ Frac {- \ alfa ^ {2 ^ {n}} - \ alfa ^ {- 2 ^ {n}} +2}{4}}}$

gdzie α jest jedną z liczb zespolonych

${\ Displaystyle \ alfa = 1-2x_ {0} \ pm {\ sqrt {\ lewo (1-2x_ {0} \ prawo) ^ {2} -1}}}$

o module równym 1. Tak jak kwadratowa funkcja sinusoidalna w rozwiązaniu trygonometrycznym nie prowadzi ani do kurczenia się, ani do rozszerzania zbioru odwiedzanych punktów, tak w tym drugim rozwiązaniu efekt ten jest realizowany przez jednostkowy moduł α .

Natomiast rozwiązaniem, gdy r = 2 jest

${\ Displaystyle x_ {n} = {\ tfrac {1} {2}} - {\ tfrac {1} {2}} \ lewo (1- 2x_{0}\prawo)^{2^{n}}}$

dla ₀ x ∈ [0,1) . Ponieważ ₀ (1 − 2 x ) ∈ (−1,1) dla dowolnej wartości x ₀ innej niż niestabilny punkt stały 0, wyraz ₀ (1 − 2 x ) ^{2 n} dąży do 0, gdy n dąży do nieskończoności, więc x _n dąży do stabilnego punktu stałego 1 / 2 .

Znajdowanie cykli o dowolnej długości, gdy r = 4

Dla przypadku r = 4 z prawie wszystkich warunków początkowych sekwencja iteracji jest chaotyczna. Niemniej jednak istnieje nieskończona liczba warunków początkowych, które prowadzą do cykli i rzeczywiście istnieją cykle o długości k dla wszystkich liczb całkowitych k > 0 . Możemy wykorzystać związek mapy logistycznej z transformacją diadyczną (znaną również jako mapa przesunięcia bitowego ), aby znaleźć cykle o dowolnej długości. Jeśli x jest zgodne z mapą logistyczną x _{n + 1} = 4 x _n (1 − x _n ) i y następuje po transformacji diadycznej

${\ Displaystyle y_ {n + 1} = {\ rozpocząć {przypadki} 2y_ {n} i 0 \ leq y_{n}<{\tfrac {1}{2}}\\2y_{n}-1&{\tfrac {1}{2}}\leq y_{n}<1,\end{przypadki}}}$

wtedy oba są powiązane homeomorfizmem

${\ Displaystyle x_ {n} = \ sin ^ {2} \ lewo (2 \ pi y_ {n} \ prawo).}$

Powodem, dla którego transformacja diadyczna jest również nazywana mapą z przesunięciem bitowym, jest to, że kiedy y jest zapisane w notacji binarnej, mapa przesuwa punkt binarny o jedno miejsce w prawo (i jeśli bit na lewo od punktu binarnego stał się „1”, to „1” jest zmieniane na „0”). Na przykład cykl o długości 3 występuje, jeśli iteracja ma 3-bitową powtarzającą się sekwencję w rozwinięciu binarnym (która nie jest również jednobitową powtarzalną sekwencją): 001, 010, 100, 110, 101 lub 011. Iteracja 001001001... odwzorowuje na 010010010..., który odwzorowuje na 100100100..., który z kolei odwzorowuje oryginalny 001001001...; więc to jest 3-cykl mapy przesunięcia bitowego. A pozostałe trzy powtarzające się sekwencje z rozwinięciem binarnym dają 3-cyklowy 110110110... → 101101101... → 011011011... → 110110110.... Każdy z tych 3-cykli można przekształcić w postać ułamkową: na przykład pierwszy podany cykl 3 można zapisać jako 1 / 7 → 2 / 7 → 4 / 7 → 1 / 7 . Korzystając z powyższego tłumaczenia z mapy przesunięcia bitowego na $0,611260467$ logistyczną, otrzymujemy odpowiedni cykl logistyczny 0,611260467... → 0,950484434... → 0,188255099... mógłby w podobny sposób przetłumaczyć inny 3-cykl przesunięcia bitowego na odpowiadający mu cykl logistyczny. Podobnie cykle o dowolnej długości k można znaleźć na mapie przesunięć bitowych, a następnie przetłumaczyć na odpowiednie cykle logistyczne.

Ponieważ jednak prawie wszystkie liczby w [0,1) są niewymierne, prawie wszystkie warunki początkowe mapy przesunięcia bitowego prowadzą do nieokresowości chaosu. Jest to jeden ze sposobów, aby zobaczyć, że mapa logistyczna r = 4 jest chaotyczna dla prawie wszystkich warunków początkowych.

Liczba cykli o (minimalnej) długości k = 1, 2, 3,… dla mapy logistycznej z r = 4 ( mapa namiotowa z μ = 2 ) jest znanym ciągiem całkowitym (sekwencja A001037 w OEIS ): 2, 1 , 2, 3, 6, 9, 18, 30, 56, 99, 186, 335, 630, 1161... Mówi nam to, że mapa logistyczna z r = 4 ma 2 stałe punkty, 1 cykl o długości 2, 2 cykle o długości 3 i tak dalej. Sekwencja ta przybiera szczególnie prostą postać dla liczby pierwszej k : 2 ⋅ 2 ^{k - 1} - 1 / k . Na przykład: 2 ⋅ 2 ^{13 - 1} - 1 / 13 = 630 to liczba cykli o długości 13. Ponieważ ten przypadek mapy logistycznej jest chaotyczny dla prawie wszystkich warunków początkowych, wszystkie te cykle o skończonej długości są niestabilne.

Pojęcia pokrewne

Feigenbaum uniwersalność map 1-D

Uniwersalność jednowymiarowych map z maksimami parabolicznymi i stałymi ${\ Displaystyle \ delta = 4,669201$ jest widoczna $...$ z mapą proponowaną jako model zabawkowy dla dyskretnej dynamiki lasera: ${\ Displaystyle x \ rightarrow Gx (1- \ tanh (x))}$ , gdzie ${\ Displaystyle x}$ oznacza amplitudę pola elektrycznego, to $wzmocnienie$ jako parametr bifurkacji.

Stopniowy wzrost w przedziale $zmienia$ dynamikę z regularnej na chaotyczną z jakościowo takim $diagramem$ dla logistycznej

Zobacz też

• Funkcja logistyczna , rozwiązanie ciągłego odpowiednika mapy logistycznej: logistyczne równanie różniczkowe .
• Stabilność Lapunowa # Definicja dla systemów o czasie dyskretnym
• Maltuzjański model wzrostu
• Punkty okresowe złożonych odwzorowań kwadratowych , których szczególnym przypadkiem jest mapa logistyczna ograniczona do linii rzeczywistej
• Radialna sieć funkcji bazowych , która ilustruje odwrotny problem dla mapy logistycznej.
• Równanie Schrödera
• Sztywne równanie

Notatki

• Grassberger, P .; Procaccia, I. (1983). „Pomiar dziwności dziwnych atraktorów”. Fizyka D. 9 (1–2): 189–208. Bibcode : 1983PhyD....9..189G . doi : 10.1016/0167-2789(83)90298-1 .
•   Grassberger, P. (1981). „O wymiarze Hausdorffa atraktorów fraktalnych”. Dziennik fizyki statystycznej . 26 (1): 173–179. Bibcode : 1981JSP....26..173G . doi : 10.1007/BF01106792 . S2CID 119833080 .
•   Sprott, Julien Clinton (2003). Analiza chaosu i szeregów czasowych . Oxford University Press. ISBN 978-0-19-850840-3 .
•   Strogatz, Steven (2000). Dynamika nieliniowa i chaos . Wydawnictwo Perseusz. ISBN 978-0-7382-0453-6 .
•   Tufillaro, Mikołaj; Abbott, Tyler; Reilly, Jeremiasz (1992). Eksperymentalne podejście do dynamiki nieliniowej i chaosu . Addison-Wesley w Nowym Jorku. ISBN 978-0-201-55441-0 .

Linki zewnętrzne

• Hiperpodręcznik Chaosu . Wprowadzenie do chaosu i fraktali.
• Interaktywna wizualizacja mapy logistycznej w postaci notatnika Jupyter
• Mapa logistyczna i chaos autorstwa Elmera G. Wiensa
• Złożoność i chaos (audiobook) autorstwa Rogera White'a. Rozdział 5 dotyczy równania logistycznego.
• „ Historia map iterowanych ” w A New Kind of Science autorstwa Stephena Wolframa . Champaign, Illinois: Wolfram Media, s. 918, 2002.
• „Bardzo krótka historia uniwersalności w podwojeniu okresu” P. Cvitanovića
• „Niezbyt krótka historia funkcji uniwersalnej” P. Cvitanovića
• Discrete Logistic Equation autorstwa Marka Bodnara na podstawie pracy Phila Ramsdena, Wolfram Demonstrations Project .
• Multiplikatywne sprzężenie 2 map logistycznych autorstwa C. Pellicer-Lostao i R. Lopez-Ruiz po pracy Eda Pegga Jr, Wolfram Demonstrations Project .
• Wykorzystanie SAGE do zbadania dyskretnego równania logistycznego