Grawitacja Marsa

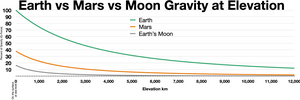
Grawitacja Ziemi vs Marsa vs Księżyca na wysokości

Grawitacja Marsa jest zjawiskiem naturalnym, wynikającym z prawa grawitacji lub grawitacji, dzięki któremu wszystkie rzeczy mające masę wokół planety Mars są przyciągane do niej. Jest słabsza niż grawitacja ziemska ze względu na mniejszą masę planety. Średnie przyspieszenie grawitacyjne na Marsie wynosi 3,72076 ms ^-2 (około 38% przyspieszenia ziemskiego ) i jest zmienne. Ogólnie rzecz biorąc, izostazja kontrolowana przez topografię napędza anomalie grawitacyjne na krótkich falach w swobodnym powietrzu . W tym samym czasie, przepływ konwekcyjny i skończona siła płaszcza prowadzą do anomalii grawitacyjnych w wolnym powietrzu na długich falach w skali planetarnej na całej planecie. Zmienność grubości skorupy, aktywność magmowa i wulkaniczna, wypiętrzenie Moho wywołane uderzeniem , sezonowe zmiany polarnych czap lodowych, zmiany masy atmosferycznej i zmiany porowatości skorupy mogą również korelować ze zmianami poprzecznymi. Z biegiem lat powstały modele składające się z rosnącej, ale ograniczonej liczby sferycznych harmonicznych . Sporządzone mapy obejmowały anomalię grawitacyjną w powietrzu , Anomalia grawitacyjna Bouguera i grubość skorupy ziemskiej. W niektórych obszarach Marsa istnieje korelacja między anomaliami grawitacyjnymi a topografią. Biorąc pod uwagę znaną topografię, można wywnioskować pole grawitacyjne o wyższej rozdzielczości. Pływowe odkształcenie Marsa przez Słońce lub Fobosa można zmierzyć jego grawitacją. To pokazuje, jak sztywne jest wnętrze i pokazuje, że rdzeń jest częściowo płynny. Badanie grawitacji powierzchniowej Marsa może zatem dostarczyć informacji o różnych cechach i dostarczyć przydatnych informacji dla przyszłych lądowań.

Pomiar

Obrotowa sferyczna harmoniczna, z

{\ Displaystyle \ ell = 0 {\ tekst {do}} 4}

dla pionu i

tekst {do}} 4}

\ poziomy. W przypadku marsjańskich C ₂₀ i C ₃₀ zmieniają się one w czasie z powodu sezonowych zmian masy polarnych czap lodowych w ramach rocznego cyklu sublimacji i kondensacji dwutlenku węgla.

Aby zrozumieć grawitację Marsa, często mierzy się jego natężenie pola grawitacyjnego g i potencjał grawitacyjny U. Po prostu, jeśli założyć, że Mars jest statycznym idealnie kulistym ciałem o promieniu R _M , pod warunkiem, że tylko jeden satelita krąży wokół Marsa po orbicie kołowej i takie oddziaływanie grawitacyjne jest jedyną siłą działającą w układzie, równanie byłoby

{\ Displaystyle {\ Frac {GMm} {r ^ {2}}} = pan \ omega ^ {2},}

gdzie G to uniwersalna stała grawitacji (powszechnie przyjmowana jako G = 6,674 × 10-11 ^m 3 ^kg -1 ^s -2 ⁾ , M to masa Marsa (najbardziej zaktualizowana wartość: 6,41693 × 10 ²³ kg), m to masa satelity, r to odległość między Marsem a satelitą, a to prędkość kątowa $satelity$ , która jest również ${\ Displaystyle {\ Frac {2 \ pi} {T}}}$ ( T to okres orbitowania satelity).

Dlatego ${\ Displaystyle g = {\ Frac {GM} {R_ {M} ^ {2}}} ={\frac {r^{3}\omega ^{2}}{R_{M}^{2}}}={\frac {4r^{3}\pi ^{2}}{T^{2 }R_{M}^{2}}}}$ , gdzie R _M jest promieniem Marsa. RM _Przy prawidłowym pomiarze r , T i są parametrami możliwymi do uzyskania z Ziemi.

Ponieważ jednak Mars jest ogólnym, niesferycznym ciałem planetarnym, na które wpływają złożone procesy geologiczne, dokładniej potencjał grawitacyjny jest opisywany sferycznymi funkcjami harmonicznymi , zgodnie z konwencją geodezyjną; zobacz Model geopotencjału .

{\ Displaystyle U (r, \ lambda, \ psi) = - {\ Frac {GM} {r}} \ lewo (

gdzie ${\ displaystyle r, \ psi, \ lambda}$ są współrzędnymi sferycznymi badanego punktu. ${\ Displaystyle \ lambda}$ to długość geograficzna, a $szerokość$ geograficzna. ${\ Displaystyle C _ {\ ell m}}$ i $ell m}}$ $\$ są bezwymiarowymi współczynnikami harmonicznymi stopnia rzędu ${\ displaystyle m}$ . ${\ Displaystyle P _ {\ ell} ^ {m}}$ jest wielomianem Legendre'a stopnia z $\$ $Displaystyle m = 0}$ i jest powiązanym wielomianem Legendre'a z ${\ Displaystyle m>0}$ . Służą one do opisu rozwiązań równania Laplace'a . ${\ displaystyle R}$ to średni promień planety. Współczynnik jest czasami zapisywany jako $_ {\ ell 0}}$ ${\ Displaystyle J_ {n}}$ .

Im niższy stopień $,$ porządek $tym$ długość fali anomalii reprezentuje. Z kolei na anomalię grawitacyjną na długich falach mają wpływ globalne struktury geofizyczne.
Im wyższy stopień $.$ porządek $,$ krótsza długość fali anomalii, którą reprezentuje Dla stopnia powyżej 50 wykazano, że różnice te mają wysoką korelację z topografią. Geofizyczna interpretacja cech powierzchni może dodatkowo pomóc w uzyskaniu pełniejszego obrazu marsjańskiego pola grawitacyjnego, chociaż wyniki mogą być mylące.

Najstarszą techniką określania grawitacji Marsa są obserwacje z Ziemi. Później, wraz z pojawieniem się bezzałogowych statków kosmicznych, opracowano kolejne modele grawitacji na podstawie danych śledzenia radiowego.

Naukowcy mierzyli perturbacje różnych statków kosmicznych za pomocą metod Dopplera i śledzenia odległości, aby opracować różne modele grawitacji od pierwszego przybycia bezzałogowej sondy kosmicznej Mariner 9 w 1971 r. (Źródło: NASA's Scientific Visualization Studio)

Obserwacja z Ziemi

Przed przybyciem sondy Mariner 9 i orbitera Viking na Marsa jedynie oszacowanie stałej grawitacji Marsa GM, tj. uniwersalnej stałej grawitacji pomnożonej przez masę Marsa, było dostępne do wydedukowania właściwości marsjańskiego pola grawitacyjnego. GM można uzyskać poprzez obserwacje ruchów naturalnych satelitów Marsa ( Fobosa i Deimosa ) oraz przelotów statków kosmicznych obok Marsa ( Mariner 4 i Mariner 6 ).

Długoterminowe obserwacje ruchów Fobosa i Deimosa z Ziemi dostarczają parametrów fizycznych, w tym półosi wielkiej , ekscentryczności , kąta nachylenia do płaszczyzny Laplaca itp., które pozwalają obliczyć stosunek masy Słońca do masy Marsa, moment bezwładność i współczynnik potencjału grawitacyjnego Marsa oraz podać wstępne oszacowania pola grawitacyjnego Marsa.

Wywnioskowano z danych śledzenia radiowego

Doppler trójdrożny, z oddzielnym nadajnikiem i odbiornikiem sygnału

Precyzyjne śledzenie statku kosmicznego ma pierwszorzędne znaczenie dla dokładnego modelowania grawitacji, ponieważ modele grawitacji są opracowywane na podstawie obserwacji niewielkich perturbacji statku kosmicznego, tj. niewielkich zmian prędkości i wysokości. Śledzenie odbywa się zasadniczo za pomocą anten Deep Space Network (DSN), z zastosowaniem jednokierunkowego, dwukierunkowego i trójkierunkowego Dopplera oraz śledzenia zasięgu. Śledzenie jednokierunkowe oznacza, że dane są przesyłane w jedną stronę do DSN ze statku kosmicznego, podczas gdy dwukierunkowe i trójkierunkowe obejmują przesyłanie sygnałów z Ziemi do statku kosmicznego (łącze w górę), a następnie spójnie transponowane z powrotem na Ziemię (łącze w dół) . Różnica między śledzeniem dwukierunkowym i trójkierunkowym polega na tym, że w pierwszym przypadku nadajnik i odbiornik sygnału są takie same na Ziemi, podczas gdy w drugim nadajnik i odbiornik znajdują się w różnych miejscach na Ziemi. Wykorzystanie tych trzech rodzajów danych śledzenia zwiększa zasięg i jakość danych, ponieważ jeden z nich może wypełnić lukę w danych drugiego.

Śledzenie Dopplera jest powszechną techniką śledzenia statku kosmicznego, wykorzystującą metodę prędkości radialnej, która polega na wykrywaniu przesunięć Dopplera. Gdy statek kosmiczny oddala się od nas wzdłuż linii wzroku, nastąpi przesunięcie sygnału ku czerwieni, podczas gdy w przypadku odwrotu nastąpi przesunięcie sygnału ku niebu. Taka technika została również zastosowana do obserwacji ruchu egzoplanet. Podczas gdy śledzenie zasięgu odbywa się poprzez pomiar czasu propagacji sygnału w obie strony. Połączenie przesunięcia Dopplera i obserwacji odległości sprzyja większej dokładności śledzenia statku kosmicznego.

Dane śledzenia byłyby następnie konwertowane w celu opracowania globalnych modeli grawitacji przy użyciu sferycznego równania harmonicznego pokazanego powyżej. Należy jednak przeprowadzić dalszą eliminację skutków związanych z wpływem stałego pływu , różnymi efektami relatywistycznymi związanymi ze Słońcem, Jowiszem i Saturnem, siłami niezachowawczymi (np. desaturacja momentu pędu (AMD), opór atmosferyczny i ciśnienie promieniowania słonecznego ). , w przeciwnym razie wystąpią znaczne błędy.

Historia

Najnowszym modelem grawitacyjnym dla Marsa jest Goddard Mars Model 3 (GMM-3), wyprodukowany w 2016 r., z rozwiązaniem harmonicznych sferycznych do stopnia i rzędu 120. Model ten został opracowany na podstawie 16 lat danych śledzenia radiowego z Mars Global Surveyor (MGS ), Mars Odyssey i Mars Reconnaissance Orbiter (MRO), a także model topografii MOLA i zapewnia globalną rozdzielczość 115 km. Wraz z tym modelem utworzono oddzielną mapę anomalii grawitacyjnych w powietrzu, mapę anomalii grawitacyjnej Bouguera i mapę grubości skorupy ziemskiej. W porównaniu z MRO110C i innymi poprzednimi modelami znaczna poprawa oszacowania pola grawitacyjnego wynika z dokładniejszego modelowania niezachowawczych sił działających na statek kosmiczny.

Rozwiązania grawitacyjne	Autorski	Rok	Stopień (m) i rząd (l) sferycznego rozwiązania harmonicznego [Rozdzielczość powierzchniowa (km)]	Źródło danych
–	JP Gapcyński, RH Tolson i WH Michael Jr	1977	6	Śledzenie danych statków kosmicznych Mariner 9, Viking 1 i 2
Geoide Martien	G Balmino, B Moynot i N Vales	1982	18 [¬600 km]	Śledzenie danych statków kosmicznych Mariner 9, Viking 1 i 2
GMM-1	DE Smith, FJ Lerch, RS Nerem, MT Zuber, GB Patel, SK Fricke i FG Lemoine	1993	50 [200-300 km]	Śledzenie danych statków kosmicznych Mariner 9, Viking 1 i 2
Mars50c	AS Konopliw, WL Sjogren	1995	50	Śledzenie danych statków kosmicznych Mariner 9, Viking 1 i 2
GMM-2B	FG Lemoine, DE Smith, DD Rowlands, MT Zuber, GA Neumann, DS Chinn i DE Pavlis	2001	80	Dane śledzenia Mars Global Surveyor (MGS) i dane topograficzne pochodzące z MOLA
GGM1041C	FG Lemoine	2001	90	Dane śledzenia Mars Global Surveyor (MGS) i Mars Odyssey oraz dane topograficzne pochodzące z MOLA
MGS95J	AS Konopliv, CF Yoder, EM Standish, DN Yuan, WL Sjogren	2006	95 [~112 km]	Dane śledzenia Mars Global Surveyor (MGS) i Mars Odyssey oraz dane topograficzne pochodzące z MOLA
MGGM08A	JC Marty, G Balmino, J Duron, P Rosenblatt, S Le Maistre, A Rivoldini, V Dehant, T. Van Hoolst	2009	95 [~112 km]	Dane śledzenia Mars Global Surveyor (MGS) i Mars Odyssey oraz dane topograficzne pochodzące z MOLA
MRO110B2	AS Konopliv, SW Asmar, WM Folkner, Ö Karatekin, DC Nunes, SE Smrekar, CF Yoder, MT Zuber	2011	110	Dane śledzenia Mars Global Surveyor (MGS), Mars Odyssey i Mars Reconnaissance Orbiter (MRO) oraz dane topograficzne pochodzące z MOLA
MGM2011	C Hirt, SJ Claessens, M Kuhn, MY Featherstone	2012	[3 km (równik) – 125 km]	Rozwiązanie grawitacyjne MRO110B2 i dane topograficzne pochodzące z MOLA
GMM-3	A Genova, S Goossens, FG Lemoine, E Mazarico, GA Neumann, DE Smith, MT Zuber	2016	120 [115 km]	Mars Global Surveyor (MGS), Mars Odyssey i Mars Reconnaissance Orbiter (MRO) MGS (SPO-1, SPO-2, GCO, mapa) ODY (ODYT, ODYM) MRO (MROT, MROM)

Techniki śledzenia statku kosmicznego i geofizyczna interpretacja cech powierzchni mogą wpływać na rozdzielczość natężenia pola grawitacyjnego. Lepsza technika faworyzuje sferyczne rozwiązania harmoniczne do wyższych stopni i rzędów. Niezależna analiza Mariner 9 i Viking Orbiter dane śledzenia dały stopień i rząd 6 sferycznych rozwiązań harmonicznych. Dalsze połączenie dwóch zestawów danych, wraz z korelacją anomalii z cechami wulkanicznymi (anomalia dodatnia) i głęboko drukowaną depresją (anomalia ujemna) wspomagane danymi obrazowymi pozwala na stopień i wytworzono rząd 18 sferycznych rozwiązań harmonicznych. Dalsze zastosowanie przestrzennej metody ograniczeń a priori, która uwzględniała topografię w rozwiązywaniu ograniczenia prawa potęgowego Kauli, faworyzowało model sferycznego rozwiązania harmonicznego do 50 stopnia w rozdzielczości globalnej (Goddard Mars Model-1 lub GMM-1) następnie kolejne modele o większej kompletności i stopniu i zamów do 120 na najnowszy GMM-3.

Mapa grawitacji Marsa w swobodnym powietrzu stworzona wraz z rozwiązaniem grawitacyjnym GMM-3 (Czerwony: grawitacja wysoka; Niebieski: grawitacja niska) (Źródło: NASA's Scientific Visualization Studio)

Dlatego modele grawitacyjne nie są obecnie tworzone bezpośrednio poprzez przeniesienie zmierzonych danych grawitacyjnych do dowolnego systemu informacji przestrzennej, ponieważ istnieje trudność w stworzeniu modelu o wystarczająco wysokiej rozdzielczości. Dane topograficzne uzyskane z MOLA Instrument na pokładzie Mars Global Surveyor staje się zatem użytecznym narzędziem do tworzenia bardziej szczegółowego modelu grawitacji w krótkiej skali, wykorzystującego korelację grawitacji i topografii w krótkich falach. Jednak nie wszystkie regiony Marsa wykazują taką korelację, zwłaszcza północna nizina i bieguny. Można łatwo uzyskać mylące wyniki, co może prowadzić do błędnej interpretacji geofizyki.

Późniejsze modyfikacje modelu grawitacyjnego obejmują uwzględnienie innych niezachowawczych sił działających na statek kosmiczny, w tym oporu atmosferycznego , ciśnienia promieniowania słonecznego , ciśnienia promieniowania słonecznego odbitego od Marsa , emisji termicznej Marsa i pchania statku kosmicznego, które zmniejsza lub zmniejsza moment obrotowy koła. Ponadto marsjańska precesja i przyciąganie trzeciego ciała spowodowane Słońcem , Księżycem i planet, które mogłyby wpływać na orbitę statku kosmicznego, a także wpływ relawistyczny na pomiary również powinny zostać poprawione. Czynniki te mogą prowadzić do przesunięcia rzeczywistego pola grawitacyjnego. Dokładne modelowanie jest zatem wymagane w celu wyeliminowania przesunięcia. Takie prace wciąż trwają.

Statyczne pole grawitacyjne

Wielu badaczy przedstawiło korelację między anomaliami grawitacyjnymi na krótkich falach (zmiennymi lokalnie) a topografią. W regionach o wyższej korelacji anomalie grawitacyjne w swobodnym powietrzu można rozszerzyć do wyższego stopnia poprzez geofizyczną interpretację cech powierzchni, tak aby mapa grawitacyjna mogła oferować wyższą rozdzielczość. Stwierdzono, że południowa wyżyna ma wysoką korelację grawitacji / topografii, ale nie na nizinie północnej. Dlatego rozdzielczość modelu anomalii grawitacyjnych w swobodnym powietrzu ma zwykle wyższą rozdzielczość dla półkuli południowej, nawet do ponad 100 km.

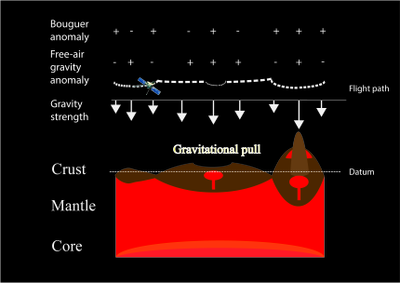
Anomalie grawitacyjne w swobodnym powietrzu są stosunkowo łatwiejsze do zmierzenia niż anomalie Bouguera , o ile dostępne są dane topograficzne, ponieważ nie trzeba eliminować efektu grawitacyjnego z powodu efektu nadwyżki masy lub niedoboru terenu po zmniejszeniu grawitacji do morza poziom. Jednak, aby zinterpretować strukturę skorupy ziemskiej, konieczna jest dalsza eliminacja takiego efektu grawitacyjnego, aby zmniejszona grawitacja była tylko wynikiem rdzenia, płaszcza i skorupy poniżej punktu odniesienia. Produktem po eliminacji są anomalie Bouguera. Jednak najważniejszym ograniczeniem w obliczeniach byłaby gęstość materiału budującego teren, który może zmieniać się poprzecznie na planecie i zależy od porowatości i geochemii skały. Odpowiednie informacje można było uzyskać z marsjańskich meteorytów i analiz in situ.

Lokalne anomalie grawitacyjne

Zmienność granicy skorupa-płaszcz, intruzja, wulkanizm i topografia mogą mieć wpływ na orbitę statku kosmicznego ze względu na większą gęstość płaszcza i materiału wulkanicznego oraz niższą gęstość skorupy. (Nie w skali) +ve: Anomalia dodatnia; -ve: Anomalia ujemna

Ponieważ anomalie grawitacyjne Bouguera mają silne powiązania z głębokością granicy skorupa-płaszcz, jedna z dodatnimi anomaliami Bouguera może oznaczać, że ma cieńszą skorupę złożoną z materiału o mniejszej gęstości i jest pod silniejszym wpływem gęstszego płaszcza i odwrotnie. Jednak może to również wynikać z różnicy w gęstości ładunku wybuchowego wulkanu i ładunku osadów, a także intruzji podpowierzchniowej i usuwania materiału. Wiele z tych anomalii jest związanych z cechami geologicznymi lub topograficznymi. Nieliczne wyjątki obejmują anomalię 63 ° E, 71 ° N, która może reprezentować rozległą zakopaną strukturę o wielkości ponad 600 km, poprzedzającą zakopaną powierzchnię wczesnonoachijską.

Anomalie topograficzne

Silna korelacja między topografią a krótkofalowymi anomaliami grawitacyjnymi w swobodnym powietrzu została wykazana zarówno w badaniach pola grawitacyjnego Ziemi, jak i Księżyca, i można to wytłumaczyć powszechnym występowaniem izostazy. Oczekuje się wysokiej korelacji dla stopnia powyżej 50 (anomalia krótkofalowa) na Marsie. I może wynosić nawet 0,9 dla stopni między 70 a 85. Taka korelacja może być wyjaśniona kompensacją zginania obciążeń topograficznych. Należy zauważyć, że starsze regiony Marsa są kompensowane izostatycznie, podczas gdy młodsze regiony są zwykle kompensowane tylko częściowo.

Anomalie z konstrukcji wulkanicznych

Mapa grawitacji Marsa Bouguera, stworzona wraz z rozwiązaniem grawitacyjnym GMM-3 w 2016 r. (Czerwony: wysoka grawitacja; Niebieski: niska grawitacja) (Źródło: NASA's Scientific Visualization Studio)

Różne konstrukty wulkaniczne mogą zachowywać się inaczej pod względem anomalii grawitacyjnych. Wulkany Olympus Mons i Tharsis Montes wytwarzają najmniejsze dodatnie anomalie grawitacyjne w swobodnym powietrzu w Układzie Słonecznym. Alba Patera , również wulkaniczne wzniesienie, na północ od Tharsis Montes , wytwarza jednak ujemną anomalię Bouguera, chociaż jej zasięg jest podobny do Olympus Mons. A dla Elysium Mons , w jego centrum stwierdzono niewielki wzrost anomalii Bouguera w ogólnym kontekście negatywnych anomalii we wzniesieniu Elysium.

Znajomość anomalii wulkanów wraz z gęstością materiału wulkanicznego byłaby przydatna w określaniu składu litosfery i ewolucji skorupy ziemskiej różnych budowli wulkanicznych. Sugerowano, że ekstrudowana lawa może wahać się od andezytu (mała gęstość) do bazaltu (wysoka gęstość), a skład może się zmieniać podczas budowy tarczy wulkanicznej, co przyczynia się do anomalii. Innym scenariuszem jest to, że materiał o dużej gęstości wtargnął pod wulkan. Takie ustawienie zaobserwowano już w przypadku słynnego Syrtis major, o którym wywnioskowano, że wymarł komora magmowa z 3300 kg m ³ pod wulkanem, wynikająca z pozytywnej anomalii Bouguera.

Anomalie z depresji

Różne zagłębienia zachowują się również inaczej w anomalii Bouguera. Gigantyczne baseny uderzeniowe, takie jak Argyre , Isidis , Hellas i Utopia , również wykazują bardzo silne dodatnie anomalie Bouguera w sposób kołowy. Te baseny były przedmiotem dyskusji pod kątem pochodzenia kraterów uderzeniowych. Jeśli tak, dodatnie anomalie mogą być spowodowane wypiętrzeniem Moho, przerzedzeniem skorupy ziemskiej i zdarzeniami modyfikacji przez osadowe i wulkaniczne obciążenia powierzchniowe po zderzeniu.

Ale jednocześnie istnieją również duże baseny, które nie są związane z taką pozytywną anomalią Bouguera, na przykład Daedalia , północna Tharsis i Elysium , które, jak się uważa, leżą pod północną równiną nizinną .

Ponadto stwierdzono, że niektóre części Coprates , Eos Chasma i Kasei Valles mają pozytywne anomalie Bouguera, chociaż są to depresje topograficzne. Może to sugerować, że zagłębienia te są podszyte płytkimi, gęstymi ciałami intruzyjnymi.

Globalne anomalie grawitacyjne

Globalne anomalie grawitacyjne, określane również jako długofalowe anomalie grawitacyjne, to harmoniczne niskiego stopnia pola grawitacyjnego, których nie można przypisać lokalnej izostazji, ale raczej skończonej sile płaszcza i różnicom gęstości w prądzie konwekcyjnym. W przypadku Marsa największą składową anomalii Bouguera jest harmoniczna pierwszego stopnia, która reprezentuje deficyt masy na półkuli południowej i nadmiar na półkuli północnej. Drugi co do wielkości składnik odpowiada spłaszczeniu planety i Tharsis .

Wczesne badania geoidy w latach pięćdziesiątych i sześćdziesiątych XX wieku koncentrowały się na harmonicznych niskiego stopnia ziemskiego pola grawitacyjnego w celu zrozumienia jego wewnętrznej struktury. Sugerowano, że takie anomalie długofalowe na Ziemi mogą być powodowane przez źródła zlokalizowane w głębokim płaszczu, a nie w skorupie, na przykład spowodowane różnicami gęstości w napędzaniu prądu konwekcyjnego, który ewoluował w czasie . Korelacja między pewnymi anomaliami topograficznymi a anomaliami grawitacyjnymi na długich falach, na przykład grzbietem środkowoatlantyckim i grzbietem Carlsberg , które mają wysoką topografię i wysoką grawitację na dnie oceanu, stały się w ten sposób argumentem za ideą prądu konwekcyjnego na Ziemi w latach 70., chociaż takie korelacje są słabe w globalnym obrazie.

Innym możliwym wyjaśnieniem anomalii w skali globalnej jest skończona wytrzymałość płaszcza (w przeciwieństwie do zerowego naprężenia), co powoduje, że grawitacja odbiega od równowagi hydrostatycznej . W przypadku tej teorii, ze względu na skończoną siłę, przepływ może nie istnieć w większości obszarów, które są niedostatecznie naprężone. A zmiany gęstości głębokiego płaszcza mogą być wynikiem niejednorodności chemicznych związanych z separacją kontynentów i bliznami pozostawionymi na Ziemi po oderwaniu księżyca. Są to przypadki sugerowane do pracy, gdy w pewnych okolicznościach dopuszcza się powolny przepływ. Jednak argumentowano, że teoria może nie być fizycznie wykonalna.

Zmienne w czasie pole grawitacyjne

Na Marsie zachodzi cykl sublimacji-kondensacji, który powoduje wymianę dwutlenku węgla między kriosferą a atmosferą. Z kolei następuje wymiana masy między dwiema sferami, co daje sezonowe wahania grawitacji. (Dzięki uprzejmości NASA/JPL-Caltech)

Sezonowa zmiana pola grawitacyjnego na biegunach

Cykl sublimacji - kondensacji dwutlenku węgla na Marsie między atmosferą a kriosferą (polarna pokrywa lodowa) przebiega sezonowo. Cykl ten jest prawie jedyną zmienną odpowiadającą za zmiany pola grawitacyjnego na Marsie. Zmierzony potencjał grawitacyjny Marsa z orbiterów można uogólnić jako równanie poniżej,

{\ Displaystyle V ({\ tekst {Mars}}) = V ({\ tekst {solidna planeta}}) + V ({\ tekst {{ czapki sezonowe}}+{\text{atmosfera}})}

Z kolei, gdy w czapach sezonowych będzie więcej masy z powodu większej kondensacji dwutlenku węgla z atmosfery, masa atmosfery spadnie. Mają odwrotny stosunek do siebie. A zmiana masy ma bezpośredni wpływ na zmierzony potencjał grawitacyjny.

Sezonowa wymiana masy między północną a południową czapą polarną wykazuje zmienność grawitacji na długich falach w czasie. Długie lata ciągłych obserwacji wykazały, że wyznaczenie parzystego strefowego, znormalizowanego współczynnika grawitacji C _{l=2, m=0} , oraz nieparzystego, strefowego, znormalizowanego współczynnika grawitacji C _{l=3, m=0} są kluczowe dla wyznaczenia zmiennego w czasie grawitacji $jest$ powodu takiej wymiany masy, gdzie $jest$ , podczas gdy porządkiem. Częściej są one reprezentowane w postaci C _lm w pracach naukowych.

Jeśli uznamy dwa bieguny za dwie różne masy punktowe, to ich masy są zdefiniowane jako:

{\ Displaystyle M_ {NP} = {\ Frac {C_ {20} + C_ {30}} {2}} \, M _ {\ tekst {Mars}}}

{\ Displaystyle M_ {SP} = {\ Frac {C_ {20} -C_ {30}} {2}} \, M _ {\ tekst {Mars}}}

Dane wskazują, że maksymalne wahania masy południowej czapy polarnej wynoszą około 8,4 × 10 ¹⁵ kg i występują w pobliżu równonocy jesiennej , podczas gdy dla północnego bieguna wynoszą około 6,2 × 10 ¹⁵ kg i występują między przesileniem zimowym a wiosną równonoc .

W dłuższej perspektywie stwierdzono, że masa lodu zmagazynowanego na biegunie północnym wzrosłaby o (1,4 ± 0,5) × 10 ¹¹ kg, a na biegunie południowym zmniejszyłaby się o (0,8 ± 0,6) × 10 ¹¹ kg. Ponadto atmosfera również w długim okresie zmniejszyłaby się pod względem masy dwutlenku węgla o (0,6 ± 0,6) × 10 ^{11 kg.} Ze względu na istnienie niepewności nie jest jasne, czy migracja materiału z bieguna południowego na biegun północny trwa, chociaż takiej możliwości nie można wykluczyć.

Fala

Dwie główne siły pływowe działające na Marsa to przypływ słoneczny i przypływ Fobosa. Liczba Love k ₂ jest ważną proporcjonalną bezwymiarową stałą odnoszącą pole pływowe działające na ciało z momentem wielobiegunowym wynikającym z rozkładu masy ciała. Zwykle k ₂ może stwierdzić odkształcenie kwadrupolowe. Znalezienie k ₂ jest pomocne w zrozumieniu struktury wnętrza Marsa. Najbardziej aktualne k ₂ uzyskane przez zespół Genova to 0,1697 ± 0,0009. Jakby _k2 jest mniejszy niż 0,10, wskazany byłby stały rdzeń, co oznacza, że przynajmniej zewnętrzny rdzeń jest płynny na Marsie, a przewidywany promień rdzenia wynosi 1520–1840 km.

Jednak obecne dane śledzenia radiowego z MGS, ODY i MRO nie pozwalają na wykrycie wpływu opóźnienia fazowego na pływy, ponieważ jest on zbyt słaby i wymaga dokładniejszego pomiaru perturbacji statku kosmicznego w przyszłości.

Implikacje geofizyczne

Grubość skorupy

Histogram procentowego pola powierzchni w stosunku do grubości skorupy Marsa: 32 km i 58 km to dwa główne szczyty histogramu.

Porównanie topografii , anomalii grawitacyjnych w powietrzu i mapy gęstości skorupy ziemskiej – Czerwony: wysoka grawitacja; Niebieski: niska grawitacja

Obecnie nie są dostępne żadne bezpośrednie pomiary grubości skorupy ziemskiej na Marsie. Implikacje geochemiczne meteorytów SNC i meteorytu ortopiroksenitu ALH84001 sugerują, że średnia grubość skorupy Marsa wynosi 100–250 km. Analiza relaksacji lepkiej sugeruje, że maksymalna grubość wynosi 50–100 km. Taka grubość ma kluczowe znaczenie dla utrzymania półkulistych zmian skorupy ziemskiej i zapobiegania przepływowi kanałów. Połączone badania geofizyki i geochemii sugerują, że średnia grubość skorupy ziemskiej może spaść do 50 ± 12 km.

Pomiar pola grawitacyjnego przez różne orbitery umożliwia stworzenie globalnego modelu potencjału Bouguera o wyższej rozdzielczości. Po wyeliminowaniu lokalnych anomalii płytkiej gęstości i efektu spłaszczenia rdzenia powstaje resztkowy potencjał Bouguera, jak wskazuje następujące równanie:

{\ Displaystyle U_ {RB} = U_ {B} -U _ {\ tekst {rdzeń}} - U _ {\ tekst {lokalny}}}

Pozostały potencjał Bouguera pochodzi z płaszcza. Falowanie granicy skorupa-płaszcz lub Moho , z poprawioną masą terenu, powinno spowodować zmianę szczątkowej anomalii. Z kolei w przypadku zaobserwowania falistej granicy powinny nastąpić zmiany w grubości skorupy.

Globalne badanie szczątkowych danych dotyczących anomalii Bouguera wskazuje, że grubość skorupy Marsa waha się od 5,8 km do 102 km. Na podstawie histogramu grubości skorupy ziemskiej zidentyfikowano dwa główne piki na 32 km i 58 km. Te dwa szczyty są powiązane z dychotomią skorupy ziemskiej Marsa. Prawie cała skorupa grubsza niż 60 km pochodzi z południowych wyżyn, o ogólnie jednolitej grubości. A północna nizina ma ogólnie cieńszą skorupę. Stwierdzono, że grubość skorupy ziemskiej regionu Arabia Terra i półkuli północnej zależy od szerokości geograficznej. Im bardziej na południe w kierunku Sinai Planum i Lunae Planum , im bardziej pogrubiona jest skorupa.

Spośród wszystkich regionów Thaumasia i Claritis zawierają najgrubszą część skorupy na Marsie, która odpowiada za histogram > 70 km. Zaobserwowano, że baseny Hellas i Argyre mają skorupę cieńszą niż 30 km, które są wyjątkowo cienkim obszarem na półkuli południowej . Zaobserwowano również, że Isidis i Utopia mają znaczne przerzedzenie skorupy ziemskiej, przy czym uważa się, że środek basenów Isidis ma najcieńszą skorupę na Marsie.

Redystrybucja skorupy przez uderzenie i lepką relaksację

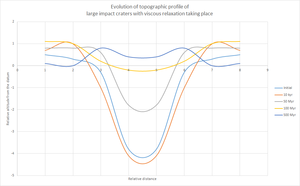
Po początkowym uderzeniu duży strumień ciepła i duża zawartość wody sprzyjałyby relaksacji lepkiej. Skórka staje się bardziej plastyczna. Topografia basenu kraterów jest zatem poddawana większym naprężeniom z powodu grawitacji własnej, która dodatkowo napędza przepływ skorupy ziemskiej i zanikanie rzeźby terenu. Jednak ta analiza może nie zadziałać w przypadku gigantycznych kraterów uderzeniowych, takich jak Hellas , Utopia , Argyre i Isidis .

Uważa się, że przerzedzenie skorupy ziemskiej miało miejsce pod prawie wszystkimi głównymi kraterami uderzeniowymi. Możliwymi przyczynami są wykopaliska skorupy ziemskiej, modyfikacja poprzez osadzanie się materiału wulkanicznego i przepływ skorupy ziemskiej w słabej litosferze. Po wydobyciu skorupy sprzed uderzenia, przywrócenie grawitacji nastąpiłoby poprzez centralne wypiętrzenie płaszcza, tak aby deficyt masy wnęki mógł zostać skompensowany masą wypiętrzonego, gęstszego materiału.

Gigantyczne baseny uderzeniowe Utopia, Hellas, Argyre i Isidis to tylko niektóre z najbardziej znanych przykładów. Utopia , basen uderzeniowy położony na nizinie północnej, jest wypełniony lekkim i osadzonym przez wodę materiałem osadowym i ma lekko pogrubioną skorupę w środku. Jest to potencjalnie spowodowane dużym procesem odnawiania powierzchni na nizinie północnej. Podczas gdy dla Hellas , Argyre i Isidis , mają one wielką wypukłą rzeźbę Moho i wykazują pierścienie rozproszonej, pogrubionej skorupy poza krawędzią skorupy.

Ale wręcz przeciwnie, prawie wszystkie baseny marsjańskie o średnicy 275 km < D < 1000 km są związane z powierzchnią o małej amplitudzie i płaskorzeźbą Moho o małej amplitudzie. Stwierdzono nawet, że wiele z nich ma ujemną anomalię grawitacyjną w swobodnym powietrzu , chociaż dowody wskazują, że wszyscy powinni doświadczyć wysokiej grawitacji (dodatnia anomalia grawitacyjna w powietrzu). Sugerowano, że nie były one spowodowane samą erozją i zakopaniem, ponieważ dodanie materiału do basenu w rzeczywistości zwiększyłoby siłę grawitacji, a nie ją zmniejszyło. Zatem lepka relaksacja powinna mieć miejsce. Wysoki strumień ciepła i wysoka zawartość wody we wczesnej skorupie marsjańskiej sprzyjały relaksacji lepkiej. Te dwa czynniki sprawiły, że skorupa stała się bardziej plastyczna. Topografia basenu kraterów byłaby narażona na większe naprężenia z powodu grawitacji własnej. Takie naprężenie spowodowałoby przepływ skorupy ziemskiej, a tym samym zanik rzeźby terenu. Gigantyczne baseny uderzeniowe to wyjątki, które nie doświadczyły lepkiej relaksacji, ponieważ przerzedzenie skorupy spowodowało, że skorupa była zbyt cienka, aby utrzymać przepływ skorupy subsolidusowej.

Niska gęstość skorupy ziemskiej

Najnowszy model gęstości skorupy ziemskiej RM1, opracowany w 2017 r., podaje gęstość skorupy ziemskiej na poziomie 2582 ± 209 kg m ^-3 dla Marsa, co stanowi średnią globalną wartość. Powinny istnieć boczne zmiany gęstości skorupy ziemskiej. Na przykład, oczekuje się, że nad kompleksami wulkanicznymi lokalna gęstość wyniesie aż 3231 ± 95 kg m ^-3 , co zgadza się z danymi meteorytowymi i wcześniejszymi szacunkami. Ponadto gęstość na półkuli północnej jest na ogół wyższa niż na półkuli południowej, co może sugerować, że ta druga jest bardziej porowata niż pierwsza.

Aby osiągnąć wartość objętościową, porowatość może odgrywać ważną rolę. Jeśli gęstość ziarna mineralnego zostanie wybrana na 3100 kg m ^-3 , porowatość od 10% do 23% może spowodować spadek gęstości nasypowej o 200 kg m ^{-3 .} Jeśli przestrzenie porów są wypełnione wodą lub lodem, spodziewany jest również spadek gęstości nasypowej. Dalszy spadek gęstości nasypowej można wytłumaczyć wzrostem gęstości wraz z głębokością, przy czym warstwa powierzchniowa jest bardziej porowata niż głębszy Mars, a wzrost gęstości wraz z głębokością ma również zróżnicowanie geograficzne.

Zastosowania inżynieryjne i naukowe

areoida

Areoid jest planetarną geoidą , która reprezentuje ekwipotencjalną figurę grawitacyjną i rotacyjną Marsa, analogiczną do koncepcji geoidy („ poziom morza ” ) na Ziemi. Zostało to ustalone jako rama odniesienia dla opracowania MEGDR (ang. Gridded Data Records) MOLA Mission Experiment, który jest globalnym modelem topografii. Model topograficzny jest ważny w mapowaniu cech geomorfologicznych i zrozumieniu różnych rodzajów procesów zachodzących na Marsie.

Do wyprowadzenia areoidy wymagane są dwie części prac. Po pierwsze, ponieważ dane grawitacyjne są niezbędne do określenia położenia środka masy planety, na które w dużej mierze wpływa rozkład masy we wnętrzu, niezbędne są dane śledzenia radiowego statku kosmicznego. Zostało to w dużej mierze zrobione przez Mars Global Surveyor (MGS). Następnie MOL 2 na pokładzie MGS, który działa na orbicie o wysokości 400 km, może mierzyć zasięg (odległość) między statkiem kosmicznym a powierzchnią ziemi, zliczając czas przelotu impulsu z instrumentu w obie strony. Połączenie tych dwóch prac pozwala na wykonanie zarówno areoidy, jak i MEGDR-ów. Na podstawie powyższego areoida przyjęła promień jako średni promień planety na równiku jako 3396 km.

Model topograficzny MEDGRs został opracowany na podstawie pomiarów zasięgu (odległości) wykonanych za pomocą instrumentu MOLA 2 oraz danych śledzenia radiowego Mars Global Surveyor (MGS). Najwyższy punkt znajduje się na Olympus Mons, a najgłębszy punkt znajduje się w Basenie Hellady. (Brązowo-czerwony: topografia wysoka; zielono-niebieski: topografia niska) (Źródło: NASA/JPL-Caltech)

Lądowanie na powierzchni

Ponieważ między Marsem a Ziemią jest duża odległość, natychmiastowe polecenie lądownikowi jest prawie niemożliwe, a lądowanie w dużej mierze zależy od jego autonomicznego systemu. Uznano, że aby uniknąć niepowodzenia, dokładne zrozumienie pola grawitacyjnego Marsa jest niezbędne dla projektów lądowania, tak aby można było zminimalizować czynniki kompensujące i niepewności efektów grawitacyjnych, umożliwiając płynny postęp lądowania. Pierwszy w historii obiekt stworzony przez człowieka lądujący na Marsie, Mars 2 lądownik, rozbił się z nieznanego powodu. Ponieważ środowisko powierzchniowe Marsa jest złożone i składa się z poprzecznie zmieniających się wzorów morfologicznych, aby uniknąć zagrożenia ze strony skał, postęp lądowania powinien być dodatkowo wspomagany przez zastosowanie LIDAR-u na miejscu w celu określenia dokładnej pozycji lądowania i innych środków ochronnych.