Monochromatyczna elektromagnetyczna fala płaska

W ogólnej teorii względności monochromatyczna elektromagnetyczna czasoprzestrzeń fali płaskiej jest analogiem monochromatycznych fal płaskich znanych z teorii Maxwella. Dokładna definicja rozwiązania jest dość skomplikowana, ale bardzo pouczająca.

Każde dokładne rozwiązanie równania pola Einsteina , które modeluje pole elektromagnetyczne , musi uwzględniać wszystkie efekty grawitacyjne energii i masy pola elektromagnetycznego . Oprócz pola elektromagnetycznego, jeśli nie ma materii i pól niegrawitacyjnych, równania pola Einsteina i równania pola Maxwella muszą być rozwiązywane jednocześnie .

W teorii pól elektromagnetyzmu Maxwella jednym z najważniejszych rodzajów pól elektromagnetycznych są pola reprezentujące elektromagnetyczne promieniowanie mikrofalowe . Spośród nich najważniejszymi przykładami są płaskie fale elektromagnetyczne , w których promieniowanie ma płaskie czoła fal poruszające się w określonym kierunku z prędkością światła. Spośród nich najbardziej podstawowe są monochromatyczne fale płaskie, w których występuje tylko jedna częstotliwość składnik jest obecny. To jest właśnie zjawisko, które model ten rozwiązanie, ale w kategoriach ogólnej teorii względności.

Definicja rozwiązania

Tensor metryczny unikalnego dokładnego rozwiązania modelującego liniowo spolaryzowaną falę płaską elektromagnetyczną o amplitudzie q i częstotliwości ω można zapisać w postaci współrzędnych Rosena

${\ Displaystyle ds ^ {2} = - 2 \, du \, dv + C ^ {2} \ lewo ({\ Frac {q ^ {2}} {\ omega ^ {2}}}, 2 {\ frac {q^{2}}{\omega ^{2}}},\omega u\right)\,\left(dx^{2}+dy^{2}\right),\qquad -\infty <v ,x,y<\infty ,\quad -u_{0}<u<u_{0}.}$

gdzie $jest$ pierwszym dodatnim $a={\frac {q^{2}}{\omega ^{2}}}$ C ( za 2 ) = , ) = 0 where . In this chart, ∂_u, ∂_v are null coordinate vectors while ∂_x, ∂_y are spacelike wektory współrzędnych.

Tutaj cosinus Mathieu C ( a , b , ξ ) jest parzystą funkcją , która rozwiązuje równanie Mathieu i również przyjmuje wartość C ( a , b , 0) = 1 . Wbrew nazwie funkcja ta nie jest okresowa i nie można jej zapisać w postaci funkcji sinusoidalnych czy nawet hipergeometrycznych. (Zobacz Funkcja Mathieu , aby uzyskać więcej informacji o funkcji cosinus Mathieu).

Zauważ, że w wyrażeniu dla metryki ∂ _u , ∂ _v są zerowymi polami wektorowymi. Dlatego ∂ _u + ∂ _v jest polem wektorowym podobnym do czasu , podczas gdy ∂ _u − ∂ _v , ∂ _x , ∂ _y to przestrzenno podobne pola wektorowe .

Aby zdefiniować potencjał wektora pola elektromagnetycznego, można przyjąć czterowektorowy potencjał elektromagnetyczny

${\ Displaystyle {\ vec {A}} = {\ Frac {{\ sqrt {2}} a \ int C \ lewo ({\ Frac {u ^ {2}} {\ omega ^ {2}}}, { \frac {q^{2}}{2\omega ^{2}}},\omega u\right)\,\sin(\omega u)\,du}{C\left({\frac {q^ {2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}}\;\częściowe _{x }}$

Jest to pełna specyfikacja modelu matematycznego sformułowanego w ogólnej teorii względności.

Lokalne izometrie

Nasza czasoprzestrzeń jest modelowana przez rozmaitość Lorentza , która ma pewne niezwykłe symetrie. Mianowicie, nasza czasoprzestrzeń dopuszcza sześciowymiarową grupę autoizometrii Liego. Ta grupa jest generowana przez sześciowymiarową algebrę Liego pól wektorowych Killing . Wygodna baza składa się z jednego zerowego pola wektorowego,

${\ Displaystyle {\ vec {\ xi}} _ {1} = \ częściowe _ {v}}$

trzy kosmiczne pola wektorowe,

${\ Displaystyle {\ vec {\ xi}} _ {2} = \ częściowe _ {x}, \ ;{\vec {\xi}}_{3}=\częściowe _{y},\;{\vec {\xi}}_{4}=-y\,\częściowe _{x}+x\, \częściowe _{y}}$

i dwa dodatkowe pola wektorowe,

${\ Displaystyle {\ rozpocząć {wyrównane} {\ vec {\ xi}} _ {5} & = x \ \ częściowe _ {v} + \ int {\ Frac {du} {C \ lewo ({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}} \,\częściowe _{x}\\{\vec {\xi}}_{6}&=y\,\częściowe _{v}+\int {\frac {du}{C\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}}\,\częściowe _{y}\end{wyrównane}}}$

${\ vec {\ xi}} _ {2}, \, {\ vec {\ xi}} _ {3}, \, {\ vec { \xi }}_{4}}$ Displaystyle generuje grupę euklidesową , działającą w obrębie każdego płaskiego czoła fali, co uzasadnia nazwę fali płaskiej dla tego rozwiązania. $\ vec {\ xi}} _ {6}}$ { pokazać, że wszystkie kierunki nie poprzeczne są równoważne. Odpowiada to faktowi, że w płaskiej czasoprzestrzeni dwie zderzające się fale płaskie zawsze zderzają się czołowo , gdy są reprezentowane w odpowiednim układzie Lorentza .

Na przyszłość zwróć uwagę, że ta sześciowymiarowa grupa samoizometrii działa przechodnio , dzięki czemu nasza czasoprzestrzeń jest jednorodna . Jednak nie jest izotropowy , ponieważ kierunki poprzeczne różnią się od kierunków nie poprzecznych.

Rodzina obserwatorów inercyjnych

Pole ramki

${\ Displaystyle {\ vec {e}} _ {0} = {\ Frac {1} {\ sqrt {2}}} \ lewo (\ częściowe _ {u} + \ częściowe _ {v} \ prawej)}$

${\ Displaystyle {\ vec {e}} _ {1} = {\ Frac {1} {\ sqrt { 2}}}\lewo(-\częściowa _{u}+\częściowa _{v}\prawa)}$

${\ Displaystyle {\ vec {e}} _ {2} = {\ Frac {1} {C \ lewo ({\ Frac {q ^ {2}}} {\ omega ^{2}}},\,{\frac {2q^{2}}{\omega ^{2}}},\,\omega u\right)}}\częściowa _{x}}$

${\ Displaystyle {\ vec {e}} _ {3} = {\ Frac {1} {C \ lewo ({\ Frac {q ^ {2}} {\ omega ^ {2}}}, \, {\ frac {2q^{2}}{\omega ^{2}}},\,\omega u\right)}}\partial _{y}}$

reprezentuje lokalną ramkę Lorentza zdefiniowaną przez rodzinę niewirujących obserwatorów inercyjnych . To jest,

${\ Displaystyle \ nabla _ {{\ vec {e}} _ {0}} {\ vec {e}} _ {0} = 0}$

co oznacza, że ​​krzywe całkowe czasopodobnego pola wektora jednostkowego e ₀ są geodezyjnymi czasopodobnymi , a także

${\ Displaystyle \ nabla _ {{\ vec {e}} _ {0}} {\ vec {e}} _ {1 }=\nabla _{{\vec {e}}_{0}}{\vec {e}}_{2}=\nabla _{{\vec {e}}_{0}}{\vec { e}}_{3}=0}$

co oznacza, że ​​przestrzennopodobne pola wektorów jednostkowych e ₁ , e ₂ , e ₃ są niewirujące. (Są one transportowane przez Fermiego-Walkera .) Tutaj ${\ displaystyle {\ vec {e}} _ {0}}$ jest czasowym jednostkowym polem wektorowym, podczas gdy ${\ displaystyle {\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3}} są$ kosmicznymi polami wektorów jednostkowych.

Nieobrotowe układy inercjalne są tak bliskie, jak tylko można w zakrzywionych czasoprzestrzeniach, zwykłym układom Lorentza znanym ze szczególnej teorii względności , gdzie transformacje Lorentza są po prostu zmianami z jednego układu Lorentza na inny.

Pole elektromagnetyczne

Jeśli chodzi o naszą ramę, pole elektromagnetyczne otrzymane z podanego powyżej potencjału wynosi

${\ Displaystyle {\ vec {E}} = q \, \ sin (\ omega u) \, {\ vec {e}} _ {2}}$

${\ Displaystyle {\ vec {B}} = - q \, \ sin (\ omega u) \, {\ vec {e}} _ {3}}$

To pole elektromagnetyczne jest rozwiązaniem bez źródła równań pola Maxwella w określonej zakrzywionej czasoprzestrzeni określonej przez tensor metryczny powyżej. Jest to rozwiązanie zerowe i reprezentuje poprzeczną sinusoidalną elektromagnetyczną falę płaską o amplitudzie q i częstotliwości ω , poruszającą się w kierunku e ₁ . Kiedy jeden

• oblicza tensor naprężenia i energii T ^ab dla zadanego pola elektromagnetycznego,
• obliczyć tensor Einsteina Gab ^, dla zadanego tensora metrycznego

okazuje się, że równanie pola Einsteina G ^ab = 8 πT ^ab jest spełnione. To właśnie oznacza stwierdzenie, że istnieje dokładne rozwiązanie w postaci elektropróżni .

Jeśli chodzi o nasz układ, tensor energii naprężenia okazuje się być

${\ Displaystyle T ^ {{\ kapelusz {j}}} {\ kapelusz {k}}} = {\ Frac {q ^{2}\sin ^{2}(\omega u)}{4\pi }}{\begin{bmatrix}1&1&0&0\\1&1&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}}}$

Jest to to samo wyrażenie , które można znaleźć w klasycznym elektromagnetyzmie (gdzie pomija się efekty grawitacyjne energii pola elektromagnetycznego) dla pola zerowego podanego powyżej; jedyna różnica polega na tym, że teraz nasz układ jest anholonomiczną (ortonormalną) bazą na zakrzywionej czasoprzestrzeni , a nie bazą współrzędnych w płaskiej czasoprzestrzeni . (Zobacz pola ramki .)

Względny ruch obserwatorów

Mówi się, że mapa Rosena porusza się wraz z naszą rodziną inercjalnych obserwatorów, ponieważ wszystkie współrzędne ve − u , x , y są stałe wzdłuż każdej linii świata, określone przez krzywą całkową czasoprzestrzennego pola wektora jednostkowego ${\ Displaystyle {\ vec {X}} = {\ vec {e}} _ {0}}$ . Tak więc na wykresie Rosena ci obserwatorzy mogą wydawać się nieruchomi. Ale w rzeczywistości poruszają się względem siebie względem siebie. Aby to zobaczyć, należy obliczyć ich tensor ekspansji w odniesieniu do układu podanego powyżej. Okazuje się, że tak

${\ Displaystyle \ theta [{\ vec {X}}] _ {{\ kapelusz {i}}} {\ kapelusz {j}}} = {\ Frac {\ omega} {\ sqrt {2}}} \, { \frac {C^{\prime}({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}} ,\omega u)}{C({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}}, \omega u)}}\,\operatorname {diag} (0,1,1)}$

Gdzie

${\ Displaystyle C ^ {\ pierwsza} (a, q, \ xi) = {\ Frac {\ częściowe C (a, q, \ xi)} {\ częściowe \ xi}}.}$

Nieznikające składniki są identyczne i są

1. wklęsły w dół na ${\ Displaystyle -u_ {0}<u <u_ {0}}$
2. zniknąć przy u = 0 .

Fizycznie oznacza to, że mała sferyczna „chmura” naszych inercyjnych obserwatorów unosi się przez chwilę w punkcie u = 0 , a następnie zaczyna się zapadać, ostatecznie przechodząc przez siebie w momencie u = u ₀ . Jeśli wyobrazimy sobie, że tworzą one trójwymiarową chmurę równomiernie rozłożonych cząstek testowych, zapadnięcie się następuje prostopadle do kierunku propagacji fali. Chmura nie wykazuje ruchu względnego w kierunku propagacji, więc jest to czysto poprzeczny .

Dla (przybliżenie krótkofalowe) ma się około ${\ Displaystyle {\ Frac {q} {\ omega}} \ ll 1}$

${\ Displaystyle g_ {xx} \ około \ cos (qu) ^ {2}}$

${\ Displaystyle \ theta [{\ vec {X}}] _ {22} \ około -q \ \ tan (qu)}$ Na przykład z ${\ Displaystyle q = 1/2, \ omega = 5}$ , jeden ma

gdzie dokładne wyrażenia są wykreślone na czerwono, a przybliżenia krótkofalowe na zielono.

Tensor wirowości naszej kongruencji znika identycznie , więc linie świata naszych obserwatorów są hiperpowierzchniowo ortogonalne . Trójwymiarowy tensor Riemanna hiperplastrów jest dany, w odniesieniu do naszego układu, przez

${\ Displaystyle {{} ^ {3} R} _ {1212} = {{} ^ {3} R} _ {1313} = q ^ {2}\,\sin(\omega u)^{2}}$

${\ Displaystyle {{} ^ {3} R} _ {2323} = {\ Frac {- \ omega ^ {2}} {2}} \, { \frac {C^{\prime}\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2} }},\omega u\right)^{2}}{C\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{ 2\omega ^{2}}},\omega u\po prawej)^{2}}}}$

Krzywizna dzieli się równo na falę (krzywizny przekroju równoległe do kierunku propagacji) i tło (krzywizna przekroju poprzecznego).

Tensor krzywizny Riemanna

W przeciwieństwie do tego, $rozkład$ Bela krzywizny Riemanna, wzięty w odniesieniu do prostotą Tensor elektrograwitacyjny , który bezpośrednio reprezentuje przyspieszenia pływowe , to

${\ Displaystyle E [{\ vec {X}}] _ {{\ kapelusz {m}} { \hat {n}}}=q^{2}\,\sin(\omega u)^{2}\,\operatorname {diag} (0,1,1)}$

Tensor magnetograwitacyjny , który bezpośrednio reprezentuje siłę spin-spin na żyroskopie niesionym przez jednego z naszych obserwatorów, to

${\ Displaystyle B [{\ vec {X}}] _ {{\ kapelusz {m}} {\ kapelusz { n}}}=q^{2}\,\sin(\omega u)^{2}{\begin{bmatrix}0&0&0\\0&0&-1\\0&1&0\end{bmatrix}}}$

( Tensor topograficzny , który reprezentuje przestrzenne krzywizny przekroju , zgadza się z tensorem elektrograwitacyjnym).

Patrząc wstecz na nasz wykres tensora metrycznego, można zauważyć, że tensor pływowy wytwarza małe sinusoidalne przyspieszenia względne o okresie ω , które są całkowicie poprzeczne do kierunku propagacji fali. Efekt grawitacyjny netto w wielu okresach ma wytworzyć cykl ekspansji i ponownego zapadania się naszej rodziny inercyjnych, nie obracających się obserwatorów. Można to uznać za efekt krzywizny tła fali .

Ten cykl ekspansji i ponownego zapadania się przypomina rozszerzające się i ponownie zapadające się modele kosmologiczne FRW i występuje z podobnego powodu: obecności niegrawitacyjnej masy-energii. W modelach FRW ta energia masowa wynika z masy cząstek pyłu; tutaj jest to spowodowane energią pola pola fal elektromagnetycznych. Tam cykl ekspansji i ponownego zapadania się zaczyna się i kończy silną osobliwością krzywizny skalarnej ; tutaj jest zwykła osobliwość współrzędnych (okoliczność, która bardzo zmyliła Einsteina i Rosena w 1937 r.). Ponadto występuje niewielka sinusoidalna modulacja rozszerzania i ponownego zapadania się.

Efekty optyczne

Ogólna zasada dotycząca fal płaskich mówi, że nie można zobaczyć, jak pociąg fal wjeżdża na stację, ale widać, jak odjeżdża . Oznacza to, że jeśli ktoś spojrzy przez nadchodzące czoła fal na odległe obiekty, nie zobaczy zniekształceń optycznych, ale jeśli odwróci się i spojrzy przez odchodzące czoła fal na odległe obiekty, zobaczy zniekształcenia optyczne. W szczególności zerowa kongruencja geodezyjna generowana przez zerowe pole wektorowe ${\ Displaystyle {\ vec {k}} = {\ vec {e}} _ {0} + {\ vec {e} }_{1}}$ ma znikające skalary optyczne , ale zerowa kongruencja geodezyjna generowana przez ${\ Displaystyle {\ vec {\ ell}} = {\ vec {e}} _ {0} - {\ vec {e }}_{1}}$ ma znikające skalary skręcania i ścinania, ale niezanikający skalar ekspansji

${\ Displaystyle \ theta = {\ sqrt {2}} \ omega \, {\ Frac {C ^ {\ pierwsza} \ lewo ({\ Frac {q ^ {2}} {\ omega ^ {2}}}, {\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}{C\left({\frac {q^{2}}{\omega ^{2} }},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}}}$

To pokazuje, że patrząc przez odchodzące czoła fal na odległe obiekty, nasi bezwładni obserwatorzy zauważą zmianę ich pozornej wielkości w taki sam sposób, jak ekspansja samej czasoprzestrzennej kongruencji geodezyjnej.

Wykres Brinkmanna

Jednym ze sposobów szybkiego sprawdzenia wiarygodności twierdzenia, że ​​u = u ₀ jest zwykłą osobliwością współrzędnych, jest przypomnienie sobie, że nasza czasoprzestrzeń jest jednorodna , więc wszystkie zdarzenia są równoważne. Aby to bezpośrednio potwierdzić i zbadać z innej perspektywy względny ruch naszych inercjalnych obserwatorów, którzy nie obracają się, można zastosować transformację współrzędnych

${\ Displaystyle u \ do u}$

${\ Displaystyle v \ do v- {\ Frac {\ kropka {r}} {2r}} \ lewo (x ^ {2} + y ^ {2} \ prawo)}$

${\ Displaystyle x \ do x/r}$

${\ Displaystyle y \ do y/r}$

Gdzie

${\ Displaystyle - {\ Frac {{\ ddot {r}} (u)} {r (u)}} = q \ sin ( \omega u)^{2}}$

To sprowadza rozwiązanie do jego reprezentacji pod względem współrzędnych Brinkmanna :

${\ Displaystyle ds ^ {2 }=-q\,\sin(\omega u)^{2}\,du^{2}-2\,du\,dv+dx^{2}+dy^{2},\qquad -\infty <u,v,x,y<\infty}$

Ponieważ można wykazać, że nowe współrzędne są geodezyjnie kompletne , współrzędne Brinkmanna definiują globalny wykres współrzędnych. Na tym wykresie widać, że nieskończona sekwencja identycznych cykli rozszerzania się i ponownego zapadania!

środki żrące

Na wykresie Brinkmanna nasze pole ramki staje się dość skomplikowane:

${\ Displaystyle {\ vec {e}} _ {0} = {\ Frac {\ częściowe _ {u} + \ częściowe _ {v}} {\ sqrt {2}}} + \ lewo \ {{\ frac { x^{2}+y^{2}}{\sqrt {2}}}\left(-q^{2}\sin(\omega u)^{2}+{\frac {\omega ^{2 }}{2}}\,{\frac {C^{\prime}\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2} }{2\omega ^{2}}},\omega u\right)^{2}}{C\left({\frac {q^{2}}{\omega ^{2}}},{\ frac {q^{2}}{2\omega ^{2}}},\omega u\prawo)^{2}}}\prawo)\częściowe _{v}\prawo\}+\lewo\{{ \frac {\omega }{2}}{\frac {C^{\prime}\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{ 2}}{2\omega ^{2}}},\omega u\right)}{C\left({\frac {q^{2}}{\omega ^{2}}},{\frac { q^{2}}{2\omega ^{2}}},\omega u\right)}}\left(x\częściowe _{x}+y\częściowe _{y}\prawe)\prawe\} }$

i tak dalej. Oczywiście, jeśli ktoś obliczy tensor ekspansji, tensor elektrograwitacyjny itd., otrzyma te same odpowiedzi, co poprzednio, ale wyrażone w nowych współrzędnych.

Uderzająca jest prostota tensora metrycznego w porównaniu ze złożonością układu. Chodzi o to, że na nowym wykresie można łatwiej zwizualizować kaustykę utworzoną przez względny ruch naszych obserwatorów. $linie$ krzywe czasopodobnego jednostkowego pola wektora geodezyjnego naszych Na wykresie Rosena pojawiają się one jako pionowe linie współrzędnych, ponieważ ten wykres się porusza.

Aby zrozumieć, jak ta sytuacja wygląda na wykresie Brinkmanna, zauważ, że gdy ω jest ekstensywne, nasze geodezyjne pole wektora jednostkowego w czasie staje się w przybliżeniu

${\ Displaystyle {\ vec {X}} \ około {\ Frac {\ częściowe _ {u} + \ częściowe _ {v}} {\ sqrt {2}}} -q \ tan (qu) \ left(x\częściowa _{x}+y\częściowa _{y}\prawa)+{\frac {x^{2}+y^{2}}{\sqrt {2}}}\,\lewa( -q^{2}\sin(\omega u)^{2}+q^{2}\tan(qu)^{2}\right)\częściowo _{v}}$

Tłumienie ostatniego terminu, wynikiem jest

Przybliżony ruch naszej rodziny obserwatorów przedstawiony na wykresie Brinkmanna

${\ Displaystyle {\ vec {X}} \ około \ częściowe _ {t} -q \ tan \ lewo ({\ frac {qu}{\sqrt {2}}}\prawo)\lewo(x\częściowo _{x}+y\częściowo _{y}\prawo)}$

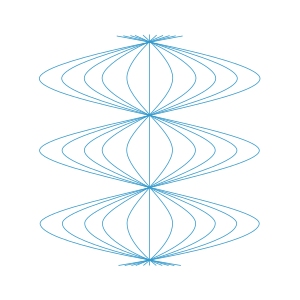
Natychmiast uzyskuje się krzywą całkową, która wykazuje cykle rozszerzania sinusoidalnego i rekonwergencji. Zobacz rysunek, na którym czas biegnie pionowo i wykorzystuje się symetrię radialną do wyeliminowania jednego wymiaru przestrzennego. Ten rysunek pokazuje, dlaczego na wykresie Rosena występuje osobliwość współrzędnych; obserwatorzy muszą przechodzić obok siebie w regularnych odstępach czasu, co jest niezgodne z właściwością współprzemieszczania się, więc wykres załamuje się w tych miejscach. Zauważ, że ta liczba błędnie sugeruje, że jeden obserwator jest niejako „centrum przyciągania”, ale w rzeczywistości wszyscy są całkowicie równoważni , ze względu na dużą grupę symetrii tej czasoprzestrzeni. Zauważ też, że szeroko sinusoidalny ruch względny naszych obserwatorów jest w pełni zgodny z zachowaniem tensora ekspansji (dotyczącego pola układu odpowiadającego naszej rodzinie obserwatorów), które zostało zauważone powyżej.

Warto zauważyć, że te nieco zawiłe punkty zdezorientowały postać nie mniej niż Alberta Einsteina w jego artykule na temat fal grawitacyjnych z 1937 roku (napisanym na długo przed tym, zanim zastosowana tutaj współczesna maszyneria matematyczna została powszechnie doceniona w fizyce).

$.$ fal krótkich są krzywymi okresowymi, które mają postać sinusoidy z okresem przez znacznie mniejsze perturbacje sinusoidalne w kierunku zerowym ∂ _v i mając znacznie krótszy okres, ${\ Displaystyle 2 \ pi / \ omega}$ . Obserwatorzy okresowo rozszerzają się i ponownie zapadają poprzecznie do kierunku propagacji; ruch ten jest modulowany przez krótki okres zaburzeń o małej amplitudzie.

Streszczenie

Porównując nasze dokładne rozwiązanie ze zwykłą monochromatyczną płaską falą elektromagnetyczną traktowaną w szczególnej teorii względności (tj. jako falę w płaskiej czasoprzestrzeni, pomijając efekty grawitacyjne energii pola elektromagnetycznego), widać, że uderzającą nową cechą ogólnej teorii cykle rozszerzania się i zapadania doświadczane przez naszych obserwatorów, które można przypisać krzywiźnie tła , a nie jakimkolwiek pomiarom dokonywanym w krótkich czasach i odległościach (rzędu długości fali elektromagnetycznego promieniowania mikrofalowego).

Zobacz też

• Argument z lepkimi koralikami , dla opisu artykułu Einsteina i Rosena z 1937 r., Do którego nawiązywał powyżej.

•   Misner, Karol; Thorne, Kip S. & Wheeler, John Archibald (1973). Grawitacja . San Francisco: WH Freeman . ISBN 0-7167-0344-0 . Patrz rozdział 35.11