Sześcienna harmoniczna

Sześcienne harmoniczne

W dziedzinach takich jak chemia obliczeniowa oraz fizyka ciała stałego i materii skondensowanej tak zwane orbitale atomowe lub spin-orbitale , pojawiające się w podręcznikach fizyki kwantowej, są często częściowo zastępowane sześciennymi harmonicznymi z wielu powodów. Te harmoniczne są zwykle nazywane harmonicznymi teseralnymi w dziedzinie fizyki materii skondensowanej, w której nazwa harmoniczne kubic odnosi się raczej do nieredukowalnych reprezentacji w sześciennej grupie punktowej.

Wstęp

Orbitale atomowe podobne do wodoru z główną liczbą kwantową $są$ liczbą kwantową momentu pędu często wyrażane jako $displaystyle$$+ 1}$

${\ Displaystyle \ psi _ {nlm} (\ mathbf {r}) = R_ {nl} (r) Y_ {l} ^{m}(\theta,\varphi)}$

w którym ${\ Displaystyle R_ {nl} (r)}$ jest promieniową częścią funkcji falowej i ${\ Displaystyle Y_ {l} ^ {m} (\ theta ,\varphi )}$ jest częścią zależną od kąta. Y ${\ Displaystyle Y_ {l} ^ {m} (\ theta, \ varphi)}$ to sferyczne harmoniczne , które są rozwiązaniami operatora pędu . Harmoniczne sferyczne są reprezentacjami funkcji pełnej grupy rotacyjnej SO(3) z symetrią obrotową. W wielu dziedzinach fizyki i chemii te harmoniczne sferyczne są zastępowane harmonicznymi sześciennymi, ponieważ symetria obrotowa atomu i jego otoczenia jest zniekształcona lub ponieważ harmoniczne sześcienne oferują korzyści obliczeniowe.

Symetria i układ współrzędnych

W wielu przypadkach, zwłaszcza w chemii oraz fizyce ciała stałego i materii skondensowanej , badany układ nie ma symetrii obrotowej. Często ma jakąś dolną symetrię , ze specjalną reprezentacją grupy punktów , lub w ogóle nie ma symetrii przestrzennej . Systemy biologiczne i biochemiczne , takie jak aminokwasy i enzymy , często należą do niskocząsteczkowych grup punktów symetrii . Stałe kryształy pierwiastków często należą do grup przestrzennych i grup punktowych o wysokiej symetrii. (Reprezentacje harmonicznych sześciennych są często wymienione i przywoływane w tabelach grup punktów ). System ma przynajmniej stałą orientację w trójwymiarowej przestrzeni euklidesowej . Dlatego układem współrzędnych używanym w takich przypadkach jest najczęściej kartezjański układ współrzędnych zamiast sferycznego układu współrzędnych . W kartezjańskim układzie współrzędnych orbitale atomowe są często wyrażane jako

${\ Displaystyle \ psi _ {nlc} (\ mathbf {r}) = R_ {nl} (r) X_ {lc} (\ matematyka {r} )}$

z sześciennymi harmonicznymi jako zestawem podstawowym ${\ Displaystyle X_ {lc} (\ mathbf {r})$ } . Obliczenia LCAO i MO w chemii obliczeniowej lub obliczenia ścisłego wiązania w fizyce ciała stałego wykorzystują harmoniczne sześcienne jako atomową podstawę orbitalną. Indeksy lc oznaczają jakąś reprezentację kartezjańską.

Przekształcenia bazowe

Dla reprezentacji sferycznych harmonicznych wybiera się sferyczny układ współrzędnych z główną osią w kierunku z . Dla harmonicznych sześciennych ta oś jest również najwygodniejszym wyborem. Dla stanów o większej liczbie kwantowej momentu pędu i wyższym wymiarze $\ Displaystyle l (l$$1)}$ liczba możliwych obrotów lub przekształceń bazowych w przestrzeni Hilberta rośnie i tak samo liczba $,$ na podstawie zbioru -wymiarowych harmonicznych Istnieje większa swoboda wyboru reprezentacji, która pasuje do symetrii grupy punktów problemu. Reprezentacje sześcienne wymienione w tabeli są wynikiem przekształceń, które są obrotami 2D o 45° i, jeśli to konieczne, obrotem o 90° do osi rzeczywistej, np.

${\ Displaystyle X_ {lc} (\ mathbf {r}) = Y_ {l} ^ {0}}$

${\ Displaystyle X_ {lc '} (\ mathbf {r}) = {\ Frac {1} {i ^ {n_ {c'}} {\ sqrt {2}}}} \ lewo (Y_ {l} ^ {m} - Y_ {l} ^ {- m} \ prawej)}$

${\ Displaystyle X_{lc''}(\mathbf {r} )={\frac {1}{i^{n_{c''}}{\sqrt {2}}}}\left(Y_{l}^{m }+Y_{l}^{-m}\prawo)}$

Znaczna liczba harmonicznych sferycznych jest wymieniona w Tabeli harmonicznych sferycznych .

Korzyści obliczeniowe

żelazocyjankowy , używany do wytwarzania „błękitu Turnbulla” z oktaedrycznie otoczonym centralnym jonem Fe ³⁺ .

Przede wszystkim harmoniczne sześcienne są funkcjami rzeczywistymi , podczas gdy harmoniczne sferyczne są funkcjami złożonymi . Liczby zespolone są dwuwymiarowe z częścią rzeczywistą i częścią urojoną. Liczby zespolone oferują bardzo dobre i skuteczne narzędzia do analitycznego rozwiązywania problemów matematycznych, ale nie są zbyt skuteczne, gdy są używane do obliczeń numerycznych. Pominięcie części urojonej pozwala zaoszczędzić połowę wysiłku obliczeniowego przy sumowaniu, współczynnik czterokrotny przy mnożeniu i często współczynnik ośmiokrotny lub nawet większy, jeśli chodzi o obliczenia wykorzystujące macierze.

Sześcienne harmoniczne często pasują do symetrii potencjału lub otoczenia atomu. Powszechnym otoczeniem atomów w ciałach stałych i kompleksach chemicznych jest otoczenie oktaedryczne z symetrią oktaedrycznej sześciennej grupy punktowej . Reprezentacje harmonicznych sześciennych często mają wysoką symetrię i krotność, więc operacje takie jak całkowanie można zredukować do ograniczonej lub nieredukowalnej części dziedziny funkcji, która ma zostać oceniona. Problem z 48-krotną ośmiościenną _Oh można obliczyć znacznie szybciej, jeśli ograniczy się obliczenia, takie jak całkowanie, do nieredukowalnej części dziedziny funkcji .

Tabela harmonicznych sześciennych

S-orbitale

S -orbitale mają tylko część promieniową.

${\ Displaystyle \ psi _ {n00} (\ mathbf {r}) = R_ {n0} (r) Y_ {0} ^ {0}}$

${\ Displaystyle s = X_ {00} = Y_ {0} ^ {0} = {\ Frac {1} {\ sqrt {4 \ pi}}}}$

	n=1	2	3	4	5	6	7
R n0

P-orbitale

Trzy orbitale p to orbitale atomowe o liczbie kwantowej momentu pędu ℓ = 1 . Sześcienne wyrażenie harmoniczne p-orbitali

${\ Displaystyle p_ {z} = N_ {1} ^ {c} {\ Frac {z} {r}} = Y_ {1} ^ {0}}$

${\ Displaystyle p_ {x} = N_ {1} ^ {c} {\ Frac {x} {r}} = {\ Frac {1 }{\sqrt {2}}}\left(Y_{1}^{-1}-Y_{1}^{1}\right)}$

${\ Displaystyle p_ {y} = N_ {1} ^ {c} {\ Frac {y} {r}} = {\ Frac {i} {\ sqrt {2}}} \ lewo (Y_ {1}^{-1}+Y_{1}^{1}\prawo)}$

z

${\ Displaystyle N_ {1} ^ {c} = \ lewo ({\ Frac {3} {4 \ pi}} \ prawo) ^ {1/2}}$

p z	px _	p y

Orbitale d

Pięć orbitali d to orbitale atomowe o liczbie kwantowej momentu pędu ℓ = 2 . Kątowa część d-orbitali jest często wyrażana jak

${\ Displaystyle \ psi _ {n2c} (\ mathbf {r}) = R_ {n2} (r) X_ {2c} (\ matematyka {r} )}$

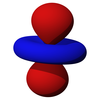
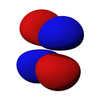
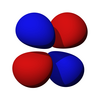
Kątowa część orbitali d to sześcienne harmoniczne ${\ Displaystyle X_ {2c} (\ mathbf {r})}$

${\ Displaystyle d_ {z ^ {2}} = N_ {2} ^ {c} {\ Frac {3z ^ {2} - r^{2}}{2r^{2}{\sqrt {3}}}}=Y_{2}^{0}}$

${\ Displaystyle d_ {xz} = N_ {2} ^ {c} {\ Frac {xz} {r ^ {2}}} = {\ Frac {1} {\ sqrt {2}}} \left(Y_{2}^{-1}-Y_{2}^{1}\right)}$

${ \ displaystyle d_ {yz} = N_ {2} ^ {c} {\ frac {yz} {r ^ {2}}} = {\ frac {i} {\ sqrt {2}}} \ lewo (Y_ {2 } ^ {- 1} + Y_ {2} ^ {1} \ prawej)}$

${\ Displaystyle d_ {xy} =N_{2}^{c}{\frac {xy}{r^{2}}}={\frac {i}{\sqrt {2}}}\left(Y_{2}^{-2} - Y_ {2} ^ {2} \ prawej)}$

${\ Displaystyle d_ {x ^{2}-y^{2}}=N_{2}^{c}{\frac {x^{2}-y^{2}}{2r^{2}}}={\frac {1 }{\sqrt {2}}}\left(Y_{2}^{-2}+Y_{2}^{2}\right)}$

z

${\ Displaystyle N_ {2} ^ {c} = \ lewo ({\ Frac {15} {4 \ pi}} \ prawo) ^ {1/2}}$

dz 2 _	d xz	d yz	d xy	d x 2 -y 2

Orbitale f

Siedem orbitali f to orbitale atomowe o liczbie kwantowej momentu pędu ℓ = 3 . często wyrażane jak

${\ Displaystyle \ psi _ {n3c} (\ mathbf {r}) = R_ {n3} (r) X_ {3c} (\ matematyka {r} )}$

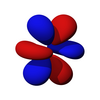
Kątowa część orbitali f to sześcienne harmoniczne ${\ Displaystyle X_ {3c} (\ mathbf {r})}$ . W wielu przypadkach wybiera się różne kombinacje liniowe harmonicznych sferycznych, aby skonstruować sześcienny zestaw bazowy f-orbitalny.

${\ Displaystyle f_ {z ^ {3}} = N_ {3} ^ {c} {\ frac {z(2z^{2}-3x^{2}-3y^{2})}{2r^{3}{\sqrt {15}}}}=Y_{3}^{0}}$

${\ Displaystyle f_ {xz ^ {2}} = N_ {3 }^{c}{\frac {x(4z^{2}-x^{2}-y^{2})}{2r^{3}{\sqrt {10}}}}={\frac { 1}{\sqrt {2}}}\left(Y_{3}^{-1}-Y_{3}^{1}\right)}$

${\ Displaystyle f_ {yz ^ {2}} = N_ {3} ^ {c} {\ Frac {y (4z ^ {2}-x^{2}-y^{2})}{2r^{3}{\sqrt {10}}}}={\frac {i}{\sqrt {2}}}\left( Y_ {3}^{-1}+Y_{3}^{1}\right)}$

${\ styl wyświetlania f_{xyz}=N_{3}^{c}{\frac {xyz}{r^{3}}}={\frac {i}{\sqrt {2}}}\left(Y_{3} ^{-2}-Y_{3}^{2}\right)}$

${\ Displaystyle f_ {z (x ^ {2} -y ^ {2})} = N_ {3} ^ {c} {\ Frac {z \ lewo (x ^ {2} -y ^ {2}\right)}{2r^{3}}}={\frac {1}{\sqrt {2}}}\left(Y_{3}^{-2}+Y_{3}^{2 } \ prawej)}$

${\ Displaystyle f_ { x(x^{2}-3y^{2})}=N_{3}^{c}{\frac {x\lewo(x^{2}-3y^{2}\prawo)}{2r^ {3}{\sqrt {6}}}}={\frac {1}{\sqrt {2}}}\left(Y_{3}^{-3}-Y_{3}^{3}\right )}$

${\ Displaystyle f_ {y (3x ^{2}-y^{2})}=N_{3}^{c}{\frac {y\lewo(3x^{2}-y^{2}\prawo)}{2r^{3} {\sqrt {6}}}}={\frac {i}{\sqrt {2}}}\left(Y_{3}^{-3}+Y_{3}^{3}\right)}$

z

${\ Displaystyle N_ {3} ^ {c} = \ lewo ({\ Frac {105} {4 \ pi}} \ prawo) ^ {1/2}}$

f z 3	f xz 2	fz 2 _	f xyz	fa z(x 2 -y 2 )	fa x(x 2 -3y 2 )	f y(3x 2 -y 2 )

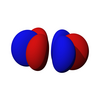Zobacz też

• Orbitale atomowe
• Fizyka atomowa
• Harmoniczne sferyczne
• Sferyczny układ współrzędnych
• Kartezjański układ współrzędnych
• Przestrzeń euklidesowa
• Przestrzeń Hilberta
• Zestaw podstawowy (chemia)
• Podstawa (algebra liniowa)
• Wektor współrzędnych
• Metoda LCAO
• Metoda ciasnego wiązania