Urodzone współrzędne
W fizyce relatywistycznej wykres współrzędnych Borna jest wykresem współrzędnych dla (części) czasoprzestrzeni Minkowskiego , płaskiej czasoprzestrzeni szczególnej teorii względności . Jest często używany do analizy fizycznych doświadczeń obserwatorów poruszających się po pierścieniu lub dysku obracającym się na sztywno z prędkościami relatywistycznymi , tzw. obserwatorów Langevina . Ten wykres jest często przypisywany Maxowi Bornowi , ze względu na jego pracę z 1909 roku nad relatywistyczną fizyką obracającego się ciała. Aby zapoznać się z przeglądem zastosowania przyspieszeń w płaskiej czasoprzestrzeni, zobacz Przyspieszenie (szczególna teoria względności) i właściwy układ odniesienia (płaska czasoprzestrzeń) .
Z doświadczenia ze scenariuszami inercjalnymi (tj. pomiarami w układach inercjalnych) obserwatorzy Langevina synchronizują swoje zegary zgodnie ze standardową konwencją Einsteina lub odpowiednio powolną synchronizacją zegarów (obie synchronizacje wewnętrzne). Dla pewnego obserwatora Langevina ta metoda sprawdza się doskonale. W jego bezpośrednim sąsiedztwie synchronizują się zegary, a światło rozchodzi się izotropowo w przestrzeni. Ale doświadczenie, gdy obserwatorzy próbują zsynchronizować swoje zegary na zamkniętej ścieżce w przestrzeni, jest zagadkowe: zawsze są co najmniej dwa sąsiednie zegary, które mają różne czasy. Aby zaradzić tej sytuacji, obserwatorzy uzgadniają zewnętrzną procedurę synchronizacji (czas współrzędnych t — lub dla obserwatorów jadących na pierścieniu, właściwy czas współrzędnych dla ustalonego promienia r ). Dzięki temu porozumieniu obserwatorzy Langevina jadący na sztywno obracającym się dysku wywnioskują z pomiarów niewielkich odległości między sobą, że geometria dysku nie jest euklidesowa. Bez względu na to, jakiej metody użyją, dojdą do wniosku, że geometria jest dobrze aproksymowana przez pewną metrykę Riemanna , a mianowicie metrykę Langevina-Landaua-Lifschitza. To z kolei bardzo dobrze przybliża geometria płaszczyzny hiperbolicznej (z ujemnymi krzywiznami odpowiednio –3 ω 2 i –3 ω 2 r 2 ). Ale jeśli ci obserwatorzy zmierzą większe odległości, uzyskają różne wyniki, w zależności od zastosowanej metody pomiaru! Jednak we wszystkich takich przypadkach najprawdopodobniej uzyskają wyniki, które są niezgodne z jakąkolwiek metryką riemannowską . W szczególności, jeśli użyją najprostszego pojęcia odległości, odległości radarowej, dzięki różnym efektom, takim jak asymetria , dojdą do wniosku, że „geometria” dysku jest nie tylko nieeuklidesowa, ale także nieriemannowska.
Obracający się dysk nie jest paradoksem . Bez względu na to, jakiej metody użyją obserwatorzy do analizy sytuacji: na końcu analizują obracający się dysk, a nie układ inercyjny.
Obserwatorzy Langevina na mapie cylindrycznej
Aby uzasadnić wykres Borna, najpierw rozważymy rodzinę obserwatorów Langevin reprezentowaną na zwykłym cylindrycznym wykresie współrzędnych dla czasoprzestrzeni Minkowskiego. Linie świata tych obserwatorów tworzą podobną do czasu kongruencję , która jest sztywna w tym sensie, że ma zanikający tensor ekspansji. Reprezentują obserwatorów, którzy sztywno obracają się wokół osi cylindrycznej symetrii.

Z elementu liniowego
możemy natychmiast odczytać pole ramki reprezentujące lokalne układy Lorentza obserwatorów stacjonarnych (inercjalnych).
Tutaj jest czasowym polem wektorów jednostkowych , podczas gdy inne są przestrzennymi polami wektorów jednostkowych; przy każdym zdarzeniu wszystkie cztery są wzajemnie ortogonalne i określają nieskończenie mały układ Lorentza statycznego obserwatora, którego linia świata przechodzi przez to zdarzenie.
pola ramki w kierunku uzyskujemy pożądane pole ramki opisujące fizyczne doświadczenie obserwatorów Langevina, a mianowicie mi →
Ta rama została najwyraźniej po raz pierwszy wprowadzona (w domyśle) przez Paula Langevina w 1935 roku; wydaje się, że jego pierwszym wyraźnym użyciem był TA Weber, dopiero w 1997 roku! Jest zdefiniowany w regionie 0 < R < 1/ω; to ograniczenie jest fundamentalne, ponieważ w pobliżu zewnętrznej granicy prędkość obserwatorów Langevina zbliża się do prędkości światła.
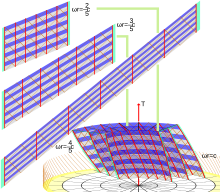
czasu pola wektora jednostkowego się na wykresie cylindrycznym jako o stałym promieniu (tak jak czerwona krzywa na ryc. 1). Załóżmy, że wybieramy jednego obserwatora Langevina i rozważamy innych obserwatorów poruszających się po pierścieniu o promieniu R, który sztywno obraca się z prędkością kątową ω. Następnie, jeśli weźmiemy krzywą całkową (niebieska spiralna krzywa na ryc. 1) kosmicznego wektora bazowego, otrzymamy krzywą, która, jak mamy nadzieję, może być interpretowane jako „linia równoczesności” dla obserwatorów jeżdżących na pierścieniu. Ale jak widzimy na ryc. 1, idealne zegary noszone przez tych obserwatorów na pierścieniu nie mogą być zsynchronizowane . To jest nasza pierwsza wskazówka, że zdefiniowanie zadowalającego pojęcia geometrii przestrzennej nie jest tak łatwe, jak można by się spodziewać, nawet dla obracającego się pierścienia , a tym bardziej obracającego się dysku!
Obliczając rozkład kinematyczny kongruencji Langevina, stwierdzamy, że wektor przyspieszenia wynosi
To jest skierowane promieniowo do wewnątrz i zależy tylko od (stałego) promienia każdej spiralnej linii świata. Tensor ekspansji znika identycznie, co oznacza, że pobliscy obserwatorzy Langevina zachowują stałą odległość od siebie. Wektor wirowości jest
która jest równoległa do osi symetrii. Oznacza to, że linie świata najbliższych sąsiadów każdego obserwatora Langevina skręcają się wokół własnej linii świata , jak sugeruje ryc. 2. Jest to rodzaj lokalnego pojęcia „wirowania” lub wirowości.
W przeciwieństwie do tego, zauważ, że rzutowanie helis na dowolny z przestrzennych hiperplastrów okrąg, który jest oczywiście krzywą zamkniętą podstawy współrzędnych jest przestrzennym polem wektora Killing , które ponadto degenerują się do zamkniętych krzywych o zerowej długości na oś R = 0. Wyraża to fakt, że nasza czasoprzestrzeń wykazuje cylindryczną symetrię , a także wykazuje rodzaj globalnego pojęcia rotacji naszych obserwatorów Langevina.
pokazuje , w jaki sposób wektory przestrzenne kręci się wokół ponieważ współrzędna Z jest nieistotna Oznacza to, że wektory nie są transportowane po świecie przez Fermiego-Walkera linia, więc rama Langevina obraca się , a także nie jest inercjalna . Innymi , w naszym prostym wyprowadzeniu układu Langevina utrzymywaliśmy układ wyrównany z wektorem bazowym . Wprowadzając stałą prędkość obrotu ramki przenoszonej przez każdego obserwatora Langevina wokół , gdybyśmy chcieli „odkręcić” naszą ramkę, aby uzyskać wersję stabilizowaną .
Transformacja do wykresu Borna
Aby otrzymać wykres Borna , wyprostowujemy helikalne linie świata obserwatorów Langevina, używając prostej transformacji współrzędnych
Nowy element liniowy to
krzyżowe” obejmujące , że wykres Borna nie jest ortogonalnych . Współrzędne Borna są czasami określane jako obracające się współrzędne cylindryczne .
Na nowym wykresie linie świata obserwatorów Langevin pojawiają się jako pionowe linie proste. Rzeczywiście, możemy łatwo przekształcić cztery pola wektorowe składające się na ramkę Langevina na nowy wykres. uzyskujemy
Są to dokładnie te same pola wektorowe, co poprzednio – są teraz po prostu reprezentowane na innym wykresie współrzędnych!
Nie trzeba dodawać, że w procesie „odwijania” linii świata obserwatorów Langevina, które na wykresie cylindrycznym pojawiają się jako helisy, „rozwijaliśmy” linie świata obserwatorów statycznych, które teraz pojawiają się jako helisy na mapie Borna ! Należy również zauważyć, że podobnie jak układ Langevina, wykres Borna jest zdefiniowany tylko w obszarze 0 < r < 1/ω.
Jeśli ponownie obliczymy rozkład kinematyczny obserwatorów Langevina, czyli o kongruencji czasowej , otrzymamy oczywiście tę samą odpowiedź, co poprzednio, tylko wyrażoną jako nowy wykres. Konkretnie, wektor przyspieszenia to
znika tensor ekspansji, a wektor wirowości jest
Podwójne pole kowektorowe pola wektora jednostkowego podobnego do czasu w dowolnym polu ramki reprezentuje nieskończenie małe przestrzenne hiperslice. Jednak twierdzenie Frobeniusa o całkowalności nakłada silne ograniczenie co do tego, czy te przestrzenne elementy hiperpłaszczyznowe mogą być „połączone razem”, aby utworzyć rodzinę przestrzennych hiperpowierzchni, które są wszędzie prostopadłe do światowych linii kongruencji. Rzeczywiście, okazuje się, że jest to możliwe, w takim przypadku mówimy, że kongruencja jest hiperpowierzchniowo ortogonalna wtedy i tylko wtedy, gdy wektor wirowości znika identycznie . Tak więc gdy obserwatorzy statyczni na wykresie cylindrycznym dopuszczają unikalną rodzinę hiperplastrów , obserwatorzy Langevina nie dopuszczają takich . W szczególności powierzchnie przestrzenne na wykresie Borna są statycznych, a nie do obserwatorów . To nasza druga (i znacznie bardziej dobitna) wskazówka, że zdefiniowanie „geometrii przestrzennej obracającego się dysku” nie jest tak proste, jak można by się spodziewać.
Aby lepiej zrozumieć ten kluczowy punkt, rozważ krzywe całkowe trzeciego wektora układu Langevina
które przechodzą przez promień . (Dla wygody usuniemy z naszych rozważań nieistotną współrzędną z). Krzywe te leżą na powierzchni
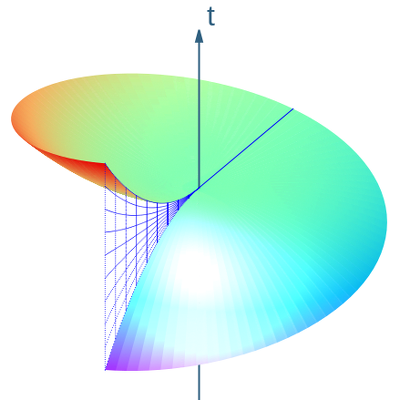
pokazano na ryc. 3. Chcielibyśmy traktować to jako „przestrzeń w czasie” dla naszych obserwatorów Langevin. Ale dwie rzeczy idą źle.
twierdzenie Frobeniusa mówi nam, że żadnego cokolwiek. Rzeczywiście , wektory nie leżą w naszym przekroju . Tak więc, chociaż znaleźliśmy hiperpowierzchnię przestrzenną, jest ona prostopadła do linii świata tylko niektórych naszych obserwatorów Langevina. Ponieważ przeszkodę wynikającą z twierdzenia Frobeniusa można rozumieć w kategoriach awarii pól wektorowych tworząc algebrę Liego , ta przeszkoda jest różniczkowa, w rzeczywistości jest teorią Liego. Oznacza to, że jest to rodzaj nieskończenie małej przeszkody w istnieniu zadowalającego pojęcia przestrzennych hiperplastrów dla naszych obracających się obserwatorów.
Po drugie, jak pokazuje ryc. 3, nasza próba hiperprzecięcia doprowadziłaby do nieciągłego pojęcia „czasu” z powodu „skoków” krzywych całkowych (pokazanych jako nieciągłość siatki w kolorze niebieskim). Alternatywnie, możemy spróbować użyć czasu wielowartościowego. Żadna z tych alternatyw nie wydaje się zbyt atrakcyjna! Jest to ewidentnie globalna przeszkoda . Jest to oczywiście konsekwencją naszej niemożności zsynchronizowania zegarów obserwatorów Langevin poruszających się choćby na jednym pierścieniu – powiedzmy na obrzeżu dysku – a tym bardziej na całym dysku .
Efekt Sagnaca
że przymocowaliśmy kabel światłowodowy na obwodzie pierścienia o promieniu który obraca się ze stałą prędkością kątową ω. Chcemy obliczyć czas podróży w obie strony, zmierzony przez obserwatora na pierścieniu, dla impulsu laserowego wysłanego zgodnie z ruchem wskazówek zegara i przeciwnie do ruchu wskazówek zegara wokół kabla. Dla uproszczenia pominiemy fakt, że światło przechodzi przez kabel światłowodowy z prędkością nieco mniejszą niż prędkość światła w próżni i będziemy udawać, że linia świata naszego impulsu laserowego jest krzywą zerową (ale z pewnością nie zerową geodezyjną ! ).
W elemencie linii Born wstawmy . To daje
Lub
Na przejazd w obie strony uzyskujemy czas przejazdu
δ , znajdujemy (dodatnie ω oznacza obrót w kierunku przeciwnym do ruchu wskazówek zegara, ujemne ω oznacza obrót w prawo), dzięki czemu obserwatorzy na pierścieniu mogą określić prędkość kątową pierścienia (mierzoną za pomocą obserwatora statycznego) z różnicy między czasem ruchu w kierunku zgodnym z ruchem wskazówek zegara i przeciwnym do ruchu wskazówek zegara. Jest to znane jako efekt Sagnaca . Jest to ewidentnie efekt globalny .
Geodezja zerowa

Chcemy porównać pojawienie się geodezji zerowej na wykresie cylindrycznym i wykresie Borna.
Na wykresie cylindrycznym odczytano równania geodezyjne
Natychmiast otrzymujemy pierwsze całki
Podłączając je do wyrażenia uzyskanego z elementu liniowego przez ustawienie , otrzymujemy
z którego widzimy, że minimalny promień geodezyjnej zerowej jest dany przez
- tj.
stąd

Możemy teraz rozwiązać, aby uzyskać geodezję zerową jako krzywe sparametryzowane przez parametr afiniczny, jak następuje:
Bardziej użyteczna dla naszych celów jest obserwacja, że trajektoria zerowej geodezji (jej rzut na dowolny przestrzenny hiperslice ) jest oczywiście linią prostą określoną przez
Aby uzyskać minimalny promień linii przechodzącej przez dwa punkty (po tej samej stronie punktu najbliższego początku układu współrzędnych), rozwiązujemy
co daje
Rozważmy teraz najprostszy przypadek, radialną geodezję zerową (R min = L = 0, E = 1, P = 0). W postaci można zapisać promieniową geodezyjną zerową geodezję skierowaną na zewnątrz
0 z promieniem R pierścienia jadącego na obserwatorze Langevina (patrz ryc. 4). Przechodząc do wykresu Borna, stwierdzamy, że trajektorię można zapisać jako
0 Ślady okazują się być lekko wygięte na wykresie Borna (patrz zielona krzywa na ryc. 4). Z rozdziału Transforming to the Born widzimy, że na wykresie Borna nie możemy poprawnie nazwać tych „śladów” jako „projekcje”, ponieważ dla obserwatora Langevin ortogonalny hiperslice dla t = t nie istnieje (patrz rys. 3).
Podobnie dla geodezji radialnej zerowej skierowanej do wewnątrz otrzymujemy
przedstawiony jako czerwona krzywa na ryc. 4.
Zauważ, że aby wysłać impuls laserowy w kierunku nieruchomego obserwatora S przy R = 0, obserwator Langevin L musi wycelować nieco w tył , aby skorygować swój własny ruch. Obracając wszystko, tak jak spodziewałby się łowca kaczek, aby wysłać impuls laserowy w kierunku obserwatora Langevina poruszającego się po obracającym się w kierunku przeciwnym do ruchu wskazówek zegara pierścieniu, obserwator centralny musi wycelować nie w aktualną pozycję tego obserwatora, ale w pozycję, w której się pojawi w samą porę, aby przechwycić sygnał. Te rodziny promieniowych geodezji zerowych skierowanych do wewnątrz i na zewnątrz reprezentują bardzo różne krzywe w czasoprzestrzeni, a ich projekcje nie są zgodne dla ω > 0.

Podobnie geodezja zerowa między obserwatorami Langevina na pierścieniu wydaje się lekko wygięta do wewnątrz na wykresie Borna, jeśli geodezja rozchodzi się z kierunkiem obrotu (patrz zielona krzywa na ryc. 5). Aby to zobaczyć, zapisz równanie geodezji zerowej na wykresie cylindrycznym w formularzu
Przekształcając do współrzędnych Borna, otrzymujemy równania
Wyeliminowanie ϕ daje
co pokazuje, że geodezja rzeczywiście wydaje się wyginać do wewnątrz (patrz ryc. 6). To też znajdujemy
Dla geodezji zerowej propagującej się w kierunku przeciwnym do obrotu (czerwona krzywa na ryc. 5) otrzymujemy
a geodezja wygina się lekko na zewnątrz. To kończy opis pojawiania się geodezji zerowej na wykresie Borna, ponieważ każda geodezja zerowa jest albo radialna, albo ma jakiś punkt najbliższego zbliżenia do osi cylindrycznej symetrii.
Zauważ (patrz ryc. 5), że obserwator na pierścieniu próbujący wysłać impuls laserowy do innego obserwatora na pierścieniu musi celować nieco przed lub za swoją współrzędną kątową, jak podano na wykresie Borna, aby skompensować ruch obrotowy celu. Zauważ też, że przedstawiony tutaj obraz jest w pełni zgodny z naszymi oczekiwaniami (patrz wygląd nocnego nieba ), że poruszający się obserwator zobaczy pozorne położenie innych obiektów na swojej sferze niebieskiej, które zostaną przesunięte w kierunku jego ruchu.
Odległość radarowa w dużej
Okazuje się, że nawet w płaskiej czasoprzestrzeni obserwatorzy przyspieszający (nawet obserwatorzy przyspieszający liniowo; patrz współrzędne Rindlera ) mogą stosować różne odrębne , ale istotne operacyjnie pojęcia odległości. Być może najprostszym z nich jest odległość radarowa .
000 Zastanów się, jak statyczny obserwator w R=0 może określić swoją odległość do obserwatora poruszającego się po pierścieniu w R=R . W zdarzeniu C wysyła impuls radarowy w kierunku pierścienia, który uderza w linię świata obserwatora jadącego na pierścieniu w punkcie A ′, a następnie powraca do obserwatora centralnego w zdarzeniu C ″. (Patrz po prawej stronie na ryc. 7). Następnie dzieli upływający czas (zmierzony za pomocą idealnego zegara, który nosi) przez dwa. Nietrudno zauważyć, że uzyskuje dla tej odległości po prostu R (na wykresie cylindrycznym) lub r (na wykresie Borna).
Podobnie obserwator poruszający się po pierścieniu może określić swoją odległość do obserwatora centralnego, wysyłając impuls radarowy w zdarzeniu A w kierunku obserwatora centralnego, który uderza w jego linię świata w zdarzeniu C ′ i wraca do obserwatora poruszającego się po pierścieniu w zdarzeniu A ″ . (Patrz schemat po lewej stronie na ryc. 7.) Nietrudno zauważyć, że uzyskuje on dla tej odległości (na wykresie cylindrycznym) lub (na wykresie Borna), wynik nieco mniejszy od uzyskanego przez obserwatora centralnego. Jest to konsekwencją dylatacji czasu: czas, jaki upłynął dla obserwatora jeżdżącego po pierścieniu, jest mniejszy o współczynnik niż czas dla obserwatora centralnego. Tak więc, chociaż odległość radarowa ma proste znaczenie operacyjne, nie jest nawet symetryczna .
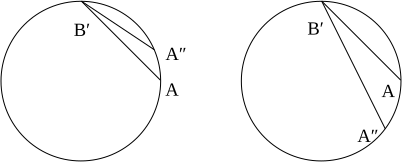
0 Aby dotrzeć do tego kluczowego punktu, porównaj odległości radarowe uzyskane przez dwóch obserwatorów poruszających się po pierścieniu ze współrzędną radialną R = R . Na schemacie po lewej stronie na ryc. 8 możemy zapisać współrzędne zdarzenia A jako
i możemy zapisać współrzędne zdarzenia B ′ jako
Zapisując nieznany czas właściwy jako , zapisujemy teraz współrzędne zdarzenia A ″ jako
0 Wymagając, aby odcinki łączące te zdarzenia były zerowe, otrzymujemy równanie, które w zasadzie możemy rozwiązać dla Δ s . Okazuje się, że ta procedura daje dość skomplikowane równanie nieliniowe, więc po prostu przedstawiamy kilka reprezentatywnych wyników liczbowych. Przy R = 1, Φ = π/2 i ω = 1/10, okazuje się, że odległość radarowa od A do B wynosi około 1,311, podczas gdy odległość od B do A wynosi około 1,510. Ponieważ ω dąży do zera, oba wyniki zmierzają w kierunku √ 2 = 1,414 (patrz także ryc. 5).
Pomimo tych potencjalnie zniechęcających rozbieżności, nie jest w żaden sposób niemożliwe opracowanie wykresu współrzędnych, który jest przystosowany do opisu fizycznego doświadczenia pojedynczego obserwatora Langevina , a nawet pojedynczego arbitralnie przyspieszającego obserwatora w czasoprzestrzeni Minkowskiego. Pauri i Vallisneri dostosowali procedurę synchronizacji zegara Märzke-Wheeler , aby opracować dostosowane współrzędne, które nazywają współrzędnymi Märzke-Wheeler (patrz artykuł cytowany poniżej). W przypadku ustalonego ruchu kołowego wykres ten jest w rzeczywistości bardzo blisko powiązany z pojęciem odległości radarowej „w dużej mierze” od danego obserwatora Langevina.
Odległość radarowa w małym
Jak wspomniano powyżej , z różnych powodów rodzina obserwatorów Langevina nie dopuszcza żadnej rodziny ortogonalnych hiperplastrów. Dlatego obserwatorów tych po prostu nie da się skojarzyć z jakimkolwiek pokrojeniem czasoprzestrzeni na rodzinę kolejnych "stałych przekrojów czasu".
Jednakże, ponieważ kongruencja Langevina jest stacjonarna , możemy sobie wyobrazić zastąpienie każdej linii świata w tej kongruencji punktem . Oznacza to, że możemy rozważyć przestrzeń ilorazową czasoprzestrzeni Minkowskiego (a raczej obszar 0 < R < 1/ ω ) przez kongruencję Langevina, która jest trójwymiarową rozmaitością topologiczną . Co więcej, możemy umieścić metrykę riemannowską na tej rozmaitości ilorazowej, przekształcając ją w trójwymiarową rozmaitość riemannowską w taki sposób, że metryka ma proste znaczenie operacyjne.
Aby to zobaczyć, rozważmy element linii Born
Ustawiając d s 2 = 0 i rozwiązując d t otrzymujemy
Właściwy czas, jaki upłynął dla impulsu radaru w obie strony, wyemitowanego przez obserwatora Langevina, wynosi wtedy
Dlatego w naszej rozmaitości ilorazowej element linii Riemanna
odpowiada odległości między nieskończenie małymi obserwatorami Langevina . Nazwiemy to metryką Langevina-Landaua-Lifschitza , a pojęcie odległości radarowej możemy nazwać „w małej” .
Ta metryka została po raz pierwszy podana przez Langevina , ale interpretacja w kategoriach odległości radarowej „w małej” pochodzi od Lwa Landaua i Evgeny'ego Lifshitza , którzy uogólnili konstrukcję, aby działała dla ilorazu dowolnej rozmaitości Lorentza przez stacjonarną kongruencję czasową.
Jeśli przyjmiemy współramę
możemy łatwo obliczyć tensor krzywizny Riemanna naszej trójwymiarowej rozmaitości ilorazowej. Ma tylko dwa niezależne nietrywialne składniki,
Tak więc w pewnym sensie geometria obracającego się dysku jest zakrzywiona , jak twierdził Theodor Kaluza (bez dowodu) już w 1910 r. W rzeczywistości, do drugiego rzędu w ω , ma on geometrię płaszczyzny hiperbolicznej, tak jak twierdził Kaluza.
Ostrzeżenie: jak widzieliśmy, istnieje wiele możliwych pojęć odległości, które mogą być stosowane przez obserwatorów Langevina jadących na sztywno obracającym się dysku, więc stwierdzenia odnoszące się do „geometrii obracającego się dysku” zawsze wymagają starannej kwalifikacji.
0 Aby przybliżyć ten ważny punkt, użyjmy metryki Landaua-Lifschitza do obliczenia odległości między obserwatorem Langevina poruszającym się po pierścieniu o promieniu R a centralnym obserwatorem statycznym. Aby to zrobić, wystarczy zintegrować nasz element liniowy na odpowiednim zerowym torze geodezyjnym. Z naszej wcześniejszej pracy wynika, że musimy podłączyć
do naszego elementu liniowego i zintegrować
To daje
Ponieważ mamy teraz do czynienia z metryką Riemanna, to pojęcie odległości jest oczywiście symetryczne przy wymianie dwóch obserwatorów, w przeciwieństwie do odległości radarowej „w dużej”. Wartości podane przez to pojęcie są sprzeczne z odległościami radarowymi „w dużym” obliczonymi w poprzedniej sekcji. Ponadto, ponieważ do drugiego rzędu metryka Landaua-Lifschitza jest zgodna z konwencją synchronizacji Einsteina, widzimy, że tensor krzywizny, który właśnie obliczyliśmy, ma znaczenie operacyjne: podczas gdy odległość radarowa „w dużej mierze” między parami obserwatorów Langevina z pewnością nie jest Riemanna pojęcie odległości , odległość między parami pobliskich obserwatorów Langevina odpowiada odległości riemannowskiej określonej przez metrykę Langevina-Landaua-Lifschitza. (W trafnym zdaniu Howarda Percy'ego Robertsona jest to kinematics im Kleinen ).
Jednym ze sposobów sprawdzenia, czy wszystkie rozsądne koncepcje odległości przestrzennej naszych obserwatorów Langevina zgadzają się z pobliskimi obserwatorami, jest wykazanie, za Nathanem Rosenem , że dla dowolnego obserwatora Langevina, poruszający się natychmiast obserwator bezwładnościowy również otrzyma odległości podane przez Langevin -Metryka Landaua-Lifschitza, dla bardzo małych odległości.
Zobacz też
- Paradoks Ehrenfesta , dla czasami kontrowersyjnego tematu, często badanego za pomocą wykresu Borna.
- Żyroskop światłowodowy
- współrzędne Rindlera jako kolejny użyteczny wykres współrzędnych dostosowany do innej ważnej rodziny przyspieszonych obserwatorów w czasoprzestrzeni Minkowskiego ; artykuł ten podkreśla również istnienie odrębnych pojęć odległości, które mogą być stosowane przez takich obserwatorów.
- Efekt Sagnaca
Kilka dokumentów o znaczeniu historycznym:
-
Urodzony, M. (1909). „Die Theorie des starren Elektrons in der Kinematik des Relativitäts-Prinzipes” . Ann. fizyka . 30 (11): 1–56. Bibcode : 1909AnP...335....1B . doi : 10.1002/andp.19093351102 .
- Tłumaczenie Wikiźródła: Teoria sztywnego elektronu w kinematyce zasady względności
-
Ehrenfest, P. (1909). „Gleichförmige Rotation starrer Körper und Relativitätstheorie”. fizyka Z. _ 10 : 918. Bibcode : 1909PhyZ...10..918E .
- Tłumaczenie Wikiźródła: Jednolity obrót ciał sztywnych i teoria względności
- Langevin, P. (1935). „Remarques au sujet de la Note de Prunier”. CR Acad. nauka Paryż . 200 : 48.
Kilka klasycznych odniesień:
- Gron, Ø. (1975). „Relatywistyczny opis obracającego się dysku”. Jestem. J. Fiz . 43 (10): 869–876. Bibcode : 1975AmJPh..43..869G . doi : 10.1119/1.9969 .
- Landau, LD i Lifschitz, EM (1980). Klasyczna teoria pól (wyd. 4) . Londyn: Butterworth-Heinemann. ISBN 0-7506-2768-9 . Zobacz sekcję 84 , aby zapoznać się z metryką Landaua-Lifschitza dotyczącą ilorazu rozmaitości Lorentza przez kongruencję stacjonarną ; patrz problem na końcu sekcji 89 dla zastosowania do obserwatorów Langevin.
Wybrane najnowsze źródła:
- Rizzi, G. & Ruggiero, ML (2004). Teoria względności w obracających się klatkach . Dordrecht: Kluwer. ISBN 1-4020-1805-3 . Ta książka zawiera cenny przegląd historyczny autorstwa Øyvinda Grøna i kilka innych artykułów na temat paradoksu Ehrenfest i związanych z nim kontrowersji oraz artykuł Lluisa Bela omawiający kongruencję Langevina. W tej książce można znaleźć setki dodatkowych odniesień.
- Pauri, Massimo & Vallisneri, Michele (2000). „Współrzędne Märzke-Wheelera dla przyspieszonych obserwatorów w szczególnej teorii względności”. Znaleziony. fizyka Lett . 13 (5): 401–425. Bibcode : 2000gr.qc.....6095P . doi : 10.1023/A:1007861914639 . S2CID 15097773 . Bada wykres współrzędnych skonstruowany przy użyciu odległości radarowej „w dużej mierze” od pojedynczego obserwatora Langevina. Zobacz także wersję eprint .
Linki zewnętrzne
- The Rigid Rotating Disk in Relativity , Michael Weiss (1995), z FAQ sci.physics .














































![{\displaystyle {\begin{aligned}R&={\sqrt {(E^{2}-P^{2})\,s^{2}+L^{2}/(E^{2}-P^{2})}}=\\&={\sqrt {(E^{2}-P^{2})\,s^{2}+R_{\mathrm {min} }^{2}}},\\T&=T_{0}+E\,s,\\[1em]Z&=Z_{0}+P\,s,\\\Phi &=\Phi _{0}+\operatorname {arctan} \left({\frac {E^{2}-P^{2}}{L}}\,s\right)=\\&=\Phi _{0}+\operatorname {arctan} \left({\frac {\sqrt {E^{2}-P^{2}}}{R_{\mathrm {min} }\,\operatorname {sgn} {(L)}}}\,s\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/417b52c09902fd606f9e9ca192947dedd154aa69)





































