Wzór na długość haka

W matematyce kombinatorycznej wzór na długość haka jest wzorem na liczbę standardowych obrazów Younga , których kształt jest danym diagramem Younga . Ma zastosowanie w różnych dziedzinach , takich jak teoria reprezentacji , prawdopodobieństwo i analiza algorytmów ; na przykład problem najdłuższych rosnących podciągów . Powiązany wzór podaje liczbę półstandardowych obrazów Younga, które są specjalizacją wielomianu Schura .

Definicje i stwierdzenie

Niech $_ {1} \ geq \ cdots \ geq \ lambda _ {k})}$${\ Displaystyle n = \ lambda _ {1} + \ cdots + \ lambda _ {k}}$ będzie podziałem n . Zwyczajowo interpretuje się graficznie jako diagram Younga $do$ lewej tablicę kwadratowych komórek z ${\ Displaystyle k}$ rzędy długości ${\ Displaystyle \ lambda _ {1}, \ ldots, \ lambda _ {k}}$ . (Standardowy) obraz Younga o kształcie $wypełnieniem$ komórek ${$ Younga wszystkimi liczbami całkowitymi $\ Displaystyle \ {1, \ kropki ,n\}}$ , bez powtórzeń, tak że każdy wiersz i każda kolumna tworzą ciągi rosnące. Dla komórki w pozycji $Displaystyle (i, j)}$ { $haczyk$ , w ${ \ Displaystyle H _ {\ lambda} (i, j)}$$,$ i th kolumnie, to zbiór komórek ${\ Displaystyle (a, b)}$ takie, że za ${\ Displaystyle a = i}$ i ${\ Displaystyle b \ geq j}$ jot $\ Displaystyle a \ geq i}$ i ${\ Displaystyle b = j}$ . ${\ Displaystyle h _ {\ lambda} (i, j)}$ jot liczba komórek w ${\ Displaystyle H _ {\ lambda} (i, j)}$ .

Formuła długości haka wyraża liczbę standardowych obrazów Younga o kształcie oznaczonych przez $f ^ {\ lambda}}$$\ Displaystyle$ lub ${\ Displaystyle d _ {\ lambda}}$ , jak

${\ Displaystyle f ^ {\ lambda} = {\ Frac {n!} {\ prod h _ {\ lambda} (i, j)}},}$

gdzie iloczyn znajduje się na wszystkich komórkach diagramu Younga ${\ Displaystyle (i, j)} .$

Przykłady

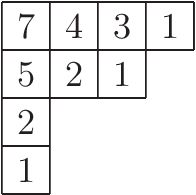
Tablica zawierająca długość haka każdej komórki na diagramie Younga ${\ Displaystyle (4,3,1,1)}$

Rysunek po prawej stronie pokazuje długości haków dla komórek na diagramie Younga ${\ Displaystyle \ lambda = (4,3,1,1)}$ , odpowiadające podziałowi 9 = 4 + 3 + 1 + 1. Wzór na długość haka podaje liczbę standardowych obrazów Younga jako:

${\ Displaystyle f ^ {\ lambda} = {\ Frac {9!} {7 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2\ckropka 2\ckropka 1\ckropka 1\ckropka 1}}=216.}$

Liczba katalońska liczy ścieżki Dycka ze stopniami ${$ górę (U) przeplatanymi $krokami$ w dół (D), tak że na każdym kroku jest do $n}$ nigdy nie są bardziej poprzedzające D niż U. Są one w bijekcji z obrazami Younga o kształcie ${\ Displaystyle \ lambda = (n, n)}$ : ścieżka Dycka odpowiada tableau, którego pierwszy wiersz zawiera pozycje U-kroków, podczas gdy drugi wiersz zawiera pozycje D-kroków. Na przykład UUDDUD odpowiada obrazom z wierszami 125 i 346.

To pokazuje, że $formuła$ formule

${\ Displaystyle C_ {n} = {\ Frac {(2n)!} {(n + 1) (n) \ cdots (3) (2) (n) (n-1) \ cdots (2) (1) }}={\frac {(2n)!}{(n+1)!\,n!}}={\frac {1}{n{+}1}}{\binom {2n}{n}} .}$

Historia

Istnieją inne wzory na $,$ na długość haka jest szczególnie prosty i elegancki. Mniej wygodny wzór wyrażający $wyznacznik$ został wydedukowany niezależnie przez Frobeniusa i Younga odpowiednio algebraicznych. MacMahon znalazł alternatywny dowód na wzór Younga-Frobeniusa w 1916 roku, używając metod różnicowych.

Sama formuła długości haczyka została odkryta w 1953 roku przez Frame'a, Robinsona i Thralla jako ulepszenie formuły Younga-Frobeniusa. Sagan opisuje odkrycie w następujący sposób.

Pewnego czwartku w maju 1953 roku Robinson odwiedzał Frame na Uniwersytecie Stanowym Michigan. Omawiając pracę Staala (ucznia Robinsona), Frame doprowadził do przypuszczenia formuły haka. Początkowo Robinson nie mógł uwierzyć, że istnieje taka prosta formuła, ale po wypróbowaniu kilku przykładów przekonał się i razem potwierdzili tożsamość. W sobotę udali się na University of Michigan, gdzie po wykładzie Robinsona Frame przedstawili swój nowy wynik. To zaskoczyło Thralla, który był na widowni, ponieważ właśnie tego samego dnia udowodnił ten sam wynik!

Pomimo prostoty wzoru na długość haczyka, dowód Frame-Robinson-Thrall nie jest zbyt wnikliwy i nie zapewnia żadnej intuicji co do roli haczyków. Poszukiwanie krótkiego, intuicyjnego wyjaśnienia pasującego do tak prostego wyniku dało początek wielu alternatywnym dowodom. Hillman i Grassl przedstawili pierwszy dowód, który wyjaśnia rolę haczyków w 1976 r., Udowadniając szczególny przypadek wzoru Stanleya na zawartość haczyków, o którym wiadomo, że implikuje wzór na długość haczyka. Greene , Nijenhuis i Wilf znalazł probabilistyczny dowód za pomocą chodzenia po haku, w którym długości haka pojawiają się naturalnie w 1979 r. Remmel zaadaptował oryginalny dowód Frame-Robinsona-Thralla do pierwszego dowodu bijektywnego dla wzoru na długość haka w 1982 r. Bezpośredni dowód bijektywny został po raz pierwszy odkryty przez Franzblau i Zeilberger w 1982 r. Zeilberger przekształcił również dowód chodu hakowego Greene-Nijenhuis-Wilf w dowód bijektywny w 1984 r. Prostszą bijekcję bezpośrednią ogłosili Pak i Stoyanovskii w 1992 r., a jej pełny dowód przedstawili para i Novelli w 1997 r. .

Tymczasem formuła długości haka została uogólniona na kilka sposobów. RM Thrall znalazł analogię do wzoru na długość haka dla przesuniętych Young Tableaux w 1952 r. Sagan podał dowód chodu z przesuniętym hakiem dla wzoru na długość haka dla przesuniętych obrazów Younga w 1980 r. Sagan i Yeh udowodnili wzór na długość haka dla drzew binarnych za pomocą haka chodzić w 1989 roku. Proctor podał uogólnienie poset (patrz poniżej).

Dowód probabilistyczny

Heurystyczny argument Knutha

Formułę długości haka można zrozumieć intuicyjnie za pomocą następującej heurystyki, ale niepoprawnej, argumentu zaproponowanego przez DE Knutha . Biorąc pod uwagę, że każdy element tableau jest najmniejszy na swoim haku i losowo wypełnia kształt tableau, prawdopodobieństwo, że komórka będzie zawierała minimalny element odpowiedniego haka, wynosi ${\ Displaystyle (i, j)}$ odwrotność długości haka. Mnożąc te prawdopodobieństwa przez wszystkie ${\ displaystyle i}$ i ${\ displaystyle j}$ podaje formułę. Ten argument jest błędny, ponieważ zdarzenia nie są niezależne.

Argument Knutha jest jednak słuszny dla wyliczenia oznaczeń na drzewach spełniających właściwości monotoniczności analogiczne do tych z tablicy Younga. W tym przypadku zdarzenia typu „hak”, o których mowa, są w rzeczywistości zdarzeniami niezależnymi.

Dowód probabilistyczny przy użyciu chodzenia hakowego

Jest to dowód probabilistyczny znaleziony przez C. Greene'a , A. Nijenhuisa i HS Wilfa w 1979 roku. Zdefiniuj

${\ Displaystyle e_ {\ lambda} = {\ Frac {n!} {\ prod _ {(i, j) \ in Y (\ lambda)} h _ {\ lambda} (i, j)}}.}$

Chcemy pokazać, że ${\ Displaystyle f ^ {\ lambda} = e_ {\ lambda}}$ . Pierwszy,

${\ Displaystyle f ^ {\ lambda} = \ suma _ {\ mu \ uparrow \ lambda} f ^ {\ mu},}$

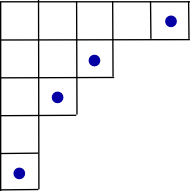
Rogi diagramu Younga (5,3,2,1,1)

$.$ suma przebiega po wszystkich diagramach Younga $uzyskanych$ usunięcia jednej komórki narożnej (Maksymalny wpis obrazu Younga o $daje$ obrazy kształtu $)$ .

Definiujemy ${\ Displaystyle f ^ {\ pusty zestaw} = 1}$ i ${\ Displaystyle e_ {\ pusty zestaw} = 1}$ , więc wystarczy pokazać ten sam cykl

${\ Displaystyle e_ {\ lambda} = \ suma _ {\ mu \ uparrow \ lambda} e_ {\ mu},}$

co oznaczałoby przez indukcję ${\ Displaystyle f ^ {\ lambda} = e_ {\ lambda}} .$ Powyższą sumę można postrzegać jako sumę prawdopodobieństw, zapisując ją jako

${\ Displaystyle \ suma _ {\ mu \ górna część \ lambda} {\ Frac {e_ {\ mu}} {e_ {\ lambda}}} = 1.}$

Dlatego musimy pokazać, że liczby $definiują$ na zbiorze diagramów Younga $Displaystyle \ mu }$ z ${\ Displaystyle \ mu \ uparrow \ lambda}$ . Odbywa się to w konstruktywny sposób poprzez zdefiniowanie spaceru losowego, zwanego marszem hakowym , na komórkach diagramu Younga , który ostatecznie wybiera jedną z narożnych komórek ${\ displaystyle \ lambda}$${\ Displaystyle \ lambda}$$\ mu \ uparrow \ lambda})$ które są w bijekcji z diagramami , dla których $Displaystyle$ . Chodzenie po haku jest określone przez następujące zasady.

1. Wybierz jednolicie losowo komórkę z ${\ Displaystyle | \ lambda |}$ komórek. Stamtąd rozpocznij losowy spacer.
2. H. $\ Displaystyle$${$ ∖ .
3. Kontynuuj, aż dotrzesz do narożnej komórki do $\ displaystyle {\ textbf {c}}}$ .

Twierdzenie: dla danej komórki narożnej mamy ${\ Displaystyle \ lambda }$$b) }$ ,

${\ Displaystyle \ mathbb {P} \ lewo ({\ textbf {c}} = (a, b) \ prawej) = {\ Frac {e_ { \mu }}{e_{\lambda }}},}$

gdzie ${\ Displaystyle \ mu = \ lambda \ setminus \ {(a, b) \}}$ .

Biorąc to pod uwagę, zsumowanie wszystkich komórek narożnych $frac$ ∑ ${e_{\mu }}{e_{\lambda }}}=1}$$Displaystyle \ suma _ {\ mu \ uparrow \ lambda$ zgodnie z deklaracją.

Połączenie z reprezentacjami grupy symetrycznej

Wzór na długość haka ma ogromne znaczenie w $displaystyle$ reprezentacji grupy symetrycznej gdzie wiadomo, że liczba jest równa wymiarowi $f ^ {\ lambda}}$ złożonej nieredukowalnej reprezentacji związanej z $}}$$lambda$ .

Szczegółowa dyskusja

Złożone nieredukowalne reprezentacje $są$ symetrycznej $indeksowane$ według $moduł$ ( Specht ) Ich postacie są związane z teorią funkcji symetrycznych poprzez iloczyn wewnętrzny Halla:

${\ Displaystyle \ chi ^ {\ lambda} (w) = \ langle s _ {\ lambda}, p _ {\ tau (w)} \ rangle, }$

gdzie ${\ Displaystyle s_ {\ lambda}}$ jest funkcją Schura powiązaną z ${\$$Displaystyle p _ {\ tau (w)}}$ jest funkcją symetryczną sumy potęgowej s λ {\ Displaystyle s_ {\ lambda} } podziału związanego z rozkładem cyklu $tau (w)}$$\ Displaystyle$ . Na przykład, jeśli ${\ Displaystyle w = (154) (238) (6) (79)}$ wtedy ${\ Displaystyle \ tau (w) = (3,3,2,1)}$ .

Ponieważ permutacja tożsamości $w$ postać mi $\ Displaystyle e = (1) (2) \ cdots (n)}$ notacji cyklicznej, ${\ Displaystyle \ tau (e) = (1, \ ldots, 1) = 1 ^ {(n)}}$ , wzór mówi

${\ Displaystyle f ^ {\ lambda} \, = \, \ dim V _ {\ lambda} \, = \, \chi ^{\lambda }(e)\,=\,\langle s_{\lambda },p_{1^{(n)}}\rangle }$

Rozwinięcie funkcji Schura w kategoriach jednomianowych funkcji symetrycznych wykorzystuje liczby Kostki :

${\ Displaystyle s _ {\ lambda} = \ suma _ {\ mu} K _ {\ lambda \ mu} m_ {\ mu},}$

Wtedy iloczyn wewnętrzny z ${\ Displaystyle p_ {1 ^ {(n)}} = h_ {1 ^ {(n)}}}$ to ${\ displaystyle K _ {\ lambda 1 ^ {(n)}}}$ , ponieważ ${\ Displaystyle \ langle m_ {\ mu}, h _ {\ nu} \ rangle = \ delta _ { \mu \nu }}$ . Zauważ, ${\ Displaystyle K _ {\ lambda 1 ^ {(n)}}}$ jest równe ${\ Displaystyle f ^ {\ lambda} = \ dim V_ {\ lambda}}$ , więc ${\ Displaystyle \ textstyle \ suma _ {\ lambda \ vdash n} \ lewo (f ^ {\ lambda} \ prawej) ^ {2} = n!}$ z rozważenia regularnej reprezentacji ${\ Displaystyle S_ {n} }$ lub kombinatorycznie z korespondencji Robinson – Schensted – Knuth .

Z obliczeń wynika również, że:

${\ Displaystyle (x_ {1} + x_ {2} + \ cdots + x_ {k}) ^ {n} = \ suma _ {\ lambda \ vdash n} s_ {\ lambda} f ^ {\ lambda}.}$

Jest to rozwinięcie ${\ Displaystyle \ langle s_ {\ mu}, s _ {\ nu} \ rangle = \ delta _ {\ mu \ nu}}$$ponieważ$ przy użyciu współczynników podanych przez . Powyższą równość można udowodnić również sprawdzając współczynniki każdego jednomianu po obu stronach i używając korespondencji Robinsona – Schensteda – Knutha $bardziej$ rozkład modułów przez moduły $przyjmując$ Zobacz dwoistość Schura – Weyla .

Dowód wzoru haka za pomocą wzoru Frobeniusa

Z powyższych rozważań

${\ Displaystyle p_ {1 ^ {(n)}} = \ suma _ {\ lambda \ vdash n} s_ {\ lambda} f ^ {\ lambda}}$

aby

${\ Displaystyle \ Delta (x) p_ {1 ^ {(n)}} = \ suma _ {\ lambda \ vdash n }\Delta (x)s_{\lambda}f^{\lambda}}$

gdzie ${\ Displaystyle \ Delta (x) = \ prod _ {i <j} (x_ {i} -x_ {j})}$ wyznacznikiem Vandermonde'a .

Dla podziału ${\ Displaystyle \ lambda = (\ lambda _ {1} \ geq \ cdots \ geq \ lambda _ {k})}$ zdefiniuj ${\ Displaystyle l_ {i} = \ lambda _ {i} + ki}$ dla ${\ Displaystyle i = 1, \ ldots, k}$ . Do poniższych potrzebujemy co najmniej tyle zmiennych , ile wierszy w podziale, więc od teraz pracujemy ze zmiennymi $x$ 1 $x_ {1}, \ cdots, x_ { n}}$ .

Każdy termin jest równy ${\ Displaystyle \ Delta (x) s_ {\ lambda}}$

${\ Displaystyle a_ {(\ lambda _ {1} + k-1, \ lambda _ {2} + k-2, \ kropki, \ lambda _ {k})} (x_ {1}, x_ {2}, \dots ,x_{k})\ =\ \det \!\left[{\begin{matrix}x_{1}^{l_{1}}&x_{2}^{l_{1}}&\dots &x_ {k}^{l_{1}}\\x_{1}^{l_{2}}&x_{2}^{l_{2}}&\kropki &x_{k}^{l_{2}}\\ \vdots &\vdots &\ddots &\vdots \\x_{1}^{l_{k}}&x_{2}^{l_{k}}&\dots &x_{k}^{l_{k}}\ koniec {macierz}}\prawo]}$

$jest$ Zobacz funkcję Schura ${\ Displaystyle x_ {1} ^ {l_ {1}} \ cdots x_ {k} ^ {l_ {k}}}$ wektor że współczynnik w ${\ Displaystyle \ Delta (x)p_{1^{(n)}}}$ , oznaczone ${\ Displaystyle \ lewo [\ Delta (x) p_ {1 ^ {(n)}} \ prawej] _ {l_ {1} , \ cdots , l_ {k}}}$ jest równe ${\ Displaystyle f ^ {\ lambda}}$ . Jest to znane jako formuła postaci Frobeniusa , która stanowi jeden z najwcześniejszych dowodów.

Pozostaje tylko uprościć ten współczynnik. Mnożenie

${\ Displaystyle \ Delta (x) \ = \ \sum _{w\in S_{n}}\operatorname {sgn}(w)x_{1}^{w(1)-1}x_{2}^{w(2)-1}\cdots x_ {k}^{w(k)-1}}$

I

${\ Displaystyle p_ {1 ^ {(n)}} \ = \ (x_ {1} + x_ {2} + \ cdots + x_ {k}) ^ {n} \ = \ \ suma {\ frac {n! }{d_{1}!d_{2}!\cdots d_{k}!}}x_{1}^{d_{1}}x_{2}^{d_{2}}\cdots x_{k}^ {d_{k}}}$

wnioskujemy, że nasz współczynnik as

${\ Displaystyle \ suma _ {w \ w S_ {n}} \ nazwa operatora {sgn} (w) {\ Frac {n!} {(l_ {1} -w (1) + 1)! \ cdots (l_ { k}-w(k)+1)!}}}$

co można zapisać jako

${\ Displaystyle {\ Frac {n!} {l_ {1}! l_ {2}! \ cdots l_ {k}!}} \ suma _ {w \ w S_ {n}} \ operatorname {sgn} (w) \left[(l_{1})(l_{1}-1)\cdots (l_{1}-w(1)+2)\right]\left[(l_{2})(l_{2}- 1)\cdots (l_{2}-w(2)+2)\right]\left[(l_{k})(l_{k}-1)\cdots (l_{k}-w(k)+ 2)\prawo]}$

Ta ostatnia suma jest równa następującemu wyznacznikowi

${\ Displaystyle \ det \ lewo [{\ rozpocząć {macierz} 1 & l_ {1} & l_ {1} (l_ {1} -1) & \ kropki & \ prod _ {i = 0} ^ {k-2} (l_ {1}-i)\\1&l_{2}&l_{2}(l_{2}-1)&\kropki &\prod _{i=0}^{k-2}(l_{2}-i) \\\vdots &\vdots &\vdots &\ddots &\vdots \\1&l_{k}&l_{k}(l_{k}-1)&\dots &\prod _{i=0}^{k- 2}(l_{k}-i)\koniec{macierzy}}\prawo]}$

która kolumna-redukuje się do wyznacznika Vandermonde'a i otrzymujemy wzór

${\ Displaystyle f ^ {\ lambda} = {\ Frac {n!} {l_ {1}! \, l_ {2}! \ cdots l_ {k}!}} \ prod _ {i <j} (l_ { i}-l_{j}).}$

Zauważ, że $postać$ haka pierwszego pudełka w każdym rzędzie diagramu Younga, a wyrażenie to można łatwo przekształcić w pożądaną ${\ Displaystyle {\ Frac {n!} {\ prod h _ {\ lambda} (i, j)}}}$ : jeden pokazuje ${\ Displaystyle \ textstyle l_ {i}! = \ prod _ {j> i} (l_ {i} -l_ {j}) \ cdot \ prod _ {j \ równoważnik \ lambda _ {i}} h _ {\ lambda} (i, j)}$ , gdzie ten ostatni iloczyn przebiega przez $wiersz$ diagramu Younga.

Połączenie z najdłuższymi rosnącymi podciągami

Wzór na długość haka ma również ważne zastosowania w analizie najdłuższych rosnących podsekwencji w losowych permutacjach. Jeśli ${\ Displaystyle \ sigma _ {n}}$ oznacza jednolicie losową permutację rzędu $Displaystyle$ L $L (\ sigma _ {n})}$ oznacza maksymalną długość rosnący podciąg ${\ Displaystyle \ sigma _ {n}}$ i ${\ Displaystyle \ ell _ {n}}$ oznacza oczekiwaną (średnią) wartość ${$ i Siergieja Kerowa oraz niezależnie Benjamina F. Logana i Lawrence'a A. Sheppa wykazali, że $}$$displaystyle$$}$$}}$ duży, jest w przybliżeniu równy . Jest to odpowiedź na pytanie postawione pierwotnie przez Stanisława Ulama . Dowód opiera się na tłumaczeniu pytania za pomocą Korespondencja Robinsona-Schensteda do problemu dotyczącego ograniczającego kształtu losowego obrazu Younga wybranego według miary Plancherela . Ponieważ definicja miary Plancherela obejmuje wielkość $.$ wzór na długość haka może być następnie użyty do przeprowadzenia asymptotycznej analizy kształtu granicznego, a tym samym również do udzielenia odpowiedzi na pierwotne

Pomysły Vershika-Kerova i Logana-Sheppa zostały później udoskonalone przez Jinho Baika, Percy'ego Deifta i Kurta Johanssona, którym udało się przeprowadzić znacznie dokładniejszą analizę ograniczającego zachowania maksymalnej rosnącej długości podsekwencji, udowadniając ważny wynik znany obecnie jako twierdzenie Baika – Deifta – Johanssona. Ich analiza ponownie w decydujący sposób wykorzystuje fakt, że $ma$ długość haka wykorzystała jedno z wyrażeń wyznaczników.

Powiązane formuły

Wzór na liczbę obrazów Younga o kształcie został pierwotnie wyprowadzony ze wzoru na wyznacznik Frobeniusa w związku z teorią reprezentacji: ${\ displaystyle \ lambda}$

${\ Displaystyle f (\ lambda _ {1}, \ ldots, \ lambda _ {k}) = {\ Frac {n! \, \ Delta (\ lambda _ {k}, \ lambda _ {k-1} + 1,\ldots ,\lambda _{1}+k-1)}{\lambda _{k}!\,(\lambda _{k-1}+1)!\cdots (\lambda _{1}+ k-1)!}}.}$

Długości haczyków można również wykorzystać do nadania reprezentacji iloczynu funkcji generującej dla liczby przegród w odwrotnej płaszczyźnie o danym kształcie. Jeśli λ jest podziałem pewnej liczby całkowitej p , podział n w odwrotnej płaszczyźnie o kształcie λ uzyskuje się, wypełniając pola na diagramie Younga nieujemnymi liczbami całkowitymi, tak aby wpisy sumowały się do n i nie zmniejszały się wzdłuż każdego wiersza i w dół każdej kolumny. Długości haczyków ${\ displaystyle h_ {1}, \ kropki, h_ {p}}$ można zdefiniować jak w przypadku obrazów Younga. Jeśli π _n oznacza liczbę podziałów płaszczyzny odwrotnej n o kształcie λ , to funkcję generującą można zapisać jako

${\ Displaystyle \ suma _ {n = 0} ^ {\ infty} \ pi _ {n} x ^ {n} =\prod _{k=1}^{p}(1-x^{h_{k}})^{-1}}$

Stanley odkrył inny wzór na tę samą funkcję generującą. Ogólnie rzecz biorąc, jeśli $posetem$ z $ZA$ , funkcją generującą dla odwrotnych partycji jest $\ displaystyle A}$

${\ Displaystyle {\ Frac {P (x)} {(1-x) (1-x ^ {2}) \ cdots (1-x^{n})}}}$

gdzie $jest$ wielomianem $_$ _ _ _ $_$ _

W przypadku podziału rozważamy poset w jego komórkach określonych przez relację ${\ displaystyle \ lambda}$

${\ Displaystyle (i, j) \ równoważnik (i ', j') \ iff i \ równoważnik ja' \ qquad { \textrm {i}}\qquad j\leq j'}$ .

Tak więc rozszerzenie liniowe jest po prostu standardowym obrazem Younga, tj. ${\ Displaystyle P (1) = f ^ {\ lambda}}$

Dowód wzoru haka za pomocą wzoru Stanleya

Łącząc dwa wzory na funkcje generujące, mamy

${\ Displaystyle {\ Frac {P(x)}{(1-x)(1-x^{2})\cdots (1-x^{n})}}=\prod _{(i,j)\in \lambda }( 1-x^{h_{(i,j)}})^{-1}}$

Obie strony zbiegają się wewnątrz dysku o promieniu jeden i następujące wyrażenie ma sens dla ${\ displaystyle | x| <1}$

${\ Displaystyle P (x) = {\ Frac {\ prod _ {k = 1} ^ {n} (1-x ^ {k})} {\ prod _ {(i, j) \ w \ lambda} ( 1-x^{h_{(i,j)}})}}.}$

Podstawienie 1 byłoby brutalne, ale prawa strona jest funkcją ciągłą wewnątrz dysku jednostkowego, a wielomian jest ciągły wszędzie, więc przynajmniej możemy powiedzieć

${\ Displaystyle P (1) = \ lim _ {x \ do 1} {\ Frac {\ prod _ {k = 1} ^ {n} (1-x ^ {k})} {\ prod _ {(i ,j)\in \lambda }(1-x^{h_{(i,j)}})}}.}$

Zastosowanie reguły $wzór$ Hôpitala razy daje na długość haka

${\ Displaystyle P (1) = {\ Frac {n!} {\ prod _ {(i, j) \ in \ lambda} h_ {(i, j)}}}.}$

Półstandardowa formuła długości haka tableaux

s ${\ Displaystyle s _ {\ lambda} (x_ {1}, \ ldots, x_ {k})}$$jest$ generującą półstandardowe obrazy Younga o $displaystyle \ lambda}$ i wpisy w ${\ Displaystyle \ {1, \ ldots, k \}}$ . Specjalizuję się w tym ${\ displaystyle x_ {i} = 1}$ podaje liczbę półstandardowych obrazów, które można zapisać w kategoriach długości haków:

${\ Displaystyle s_ {\ lambda} (1, \ ldots, 1) \ = \ \ prod _ {(i, j) \ in \ operatorname {Y} (\ lambda)} {\ Frac {k-i + j} {h_{\lambda}(i,j)}}.}$

Diagram Younga $\ Displaystyle$ nieredukowalnej reprezentacji specjalnej grupy liniowej $lambda$ \ re ja za sol $Displaystyle \ operatorname {diag} (x_ {1}, \ ldots, x_ {k}$ działając w tej reprezentacji. Powyższa specjalizacja jest zatem wymiarem nieredukowalnej reprezentacji, a wzór jest alternatywą dla bardziej ogólnego wzoru na wymiar Weyla .

Możemy to uściślić, biorąc główną specjalizację funkcji Schura w zmiennych ${\ Displaystyle 1, t, t ^ {2} \!, t ^ {3} \!, \ldots}$ :

${\ Displaystyle s_ {\ lambda} (1, t, t ^ {2}, \ ldots) \ = \ {\ Frac {t ^ {n \ lewo (\ lambda \ po prawej)}} {\ prod _ {(i ,j)\in Y(\lambda )}(1-t^{h_{\lambda }(i,j)})}},}$

gdzie ${\ Displaystyle n (\ lambda) = \ suma _ {i} (i {-} 1) \ lambda _ { i} = \ suma _ {i} {\ tbinom {\ lambda _ {i} '}{2}}}$ dla partycji sprzężonej ${\ Displaystyle \ lambda '}$ .

Formuła kształtu skośnego

Istnieje uogólnienie tego wzoru na skośne kształty,

${\ Displaystyle s _ {\ lambda / \ mu} (1, t, t ^ {2}, \ cdots) = \ suma _ {S \ in E (\ lambda / \ mu)} \ prod _ {(i, j )\in \lambda \setminus S}{\frac {t^{\lambda _{j}'-i}}{1-t^{h(i,j)}}}}$

$rozmieszczone$ suma jest przejmowana przez $.$ diagramy kształtu i pudełka zgodnie z

Uogólnienie do d -kompletnych pozycji

$diagramy$ można uznać za ideały skończonego rzędu w posecie , a standardowe obrazy Younga rozszerzeniami . Robert Proctor podał uogólnienie wzoru na długość haka do liczenia liniowych przedłużeń większej klasy pozycji, uogólniając zarówno drzewa, jak i diagramy skośne.

Linki zewnętrzne

• Zaskakująca matematyka najdłuższych rosnących podciągów autorstwa Dana Romika. Zawiera omówienie wzoru na długość haka i kilku jego wariantów, z zastosowaniami do matematyki najdłuższych rosnących podciągów.