Znak (matematyka)

Symbole plusa i minusa służą do pokazania znaku liczby.

W matematyce znakiem liczby rzeczywistej jest jej właściwość bycia dodatnim , ujemnym lub zerowym . W zależności od lokalnych konwencji, zero można uznać za ani dodatnie, ani ujemne (bez znaku lub unikalnego trzeciego znaku) lub można je uznać zarówno za dodatnie, jak i ujemne (mając oba znaki). ^{[ potrzebne źródło ]} Ilekroć nie wspomniano o tym konkretnie, ten artykuł jest zgodny z pierwszą konwencją.

W niektórych kontekstach warto rozważyć zero ze znakiem (takie jak reprezentacje zmiennoprzecinkowe liczb rzeczywistych w komputerach). W matematyce i fizyce wyrażenie „zmiana znaku” jest związane z generowaniem addytywnej odwrotności (negacja lub mnożenie przez -1 ) dowolnego obiektu, który pozwala na taką konstrukcję i nie jest ograniczony do liczb rzeczywistych. Dotyczy to między innymi wektorów, macierzy i liczb zespolonych, które nie są określone jako dodatnie, ujemne lub zerowe. Słowo „znak” jest również często używane do wskazania innych binarnych aspektów obiektów matematycznych, które przypominają pozytywność i negatywność, takich jak nieparzyste i parzyste (znak permutacji ), poczucie orientacji lub obrotu ( cw/ccw ), jednostronne granice , oraz inne pojęcia opisane w § Inne znaczenia poniżej.

Znak liczby

Liczby z różnych systemów liczbowych, takie jak liczby całkowite , wymierne , liczby zespolone , kwaterniony , oktoniony , ... mogą mieć wiele atrybutów, które ustalają pewne właściwości liczby. System liczbowy, który ma strukturę uporządkowanego pierścienia, zawiera unikalny numer, który po dodaniu do dowolnego numeru pozostawia ten ostatni bez zmian. Ten unikalny numer jest znany jako dodatkowy element tożsamości systemu . Na przykład liczby całkowite mają strukturę uporządkowanego pierścienia. Liczba ta jest ogólnie oznaczana jako $0$ $0$ $0.$ Ze względu na całkowity porządek w tym pierścieniu istnieją liczby większe od zera, zwane liczbami dodatnimi . Inną właściwością wymaganą do uporządkowania pierścienia jest to, że dla każdej liczby dodatniej istnieje unikalna odpowiednia liczba mniejsza niż suma z pierwotną liczbą dodatnią wynoszącą $0.$ Te liczby mniejsze niż nazywane są liczbami ujemnymi . Liczby w każdej takiej parze są ich odwrotnościami addytywnymi . Ten atrybut liczby, będący wyłącznie albo zerem $(0)$ , $0$ dodatni $(+)$ lub ujemny $(-)$ jest nazywany jego znakiem i często jest kodowany odpowiednio jako liczby rzeczywiste , $1$ i $-1$ (podobnie jak definiowana jest funkcja znaku ). Ponieważ liczby wymierne i rzeczywiste są również uporządkowanymi pierścieniami (w rzeczywistości uporządkowanymi polami ), atrybut znaku ma również zastosowanie do tych systemów liczbowych.

$0$ Kiedy znak minus jest używany między dwiema liczbami, reprezentuje binarną operację odejmowania. Kiedy znak minus jest zapisywany przed pojedynczą liczbą, reprezentuje jednoargumentową operację dającą addytywną odwrotność (czasami nazywaną negacją ) operandu. Abstrakcyjnie więc różnica dwóch liczb jest sumą miniendu z addytywną odwrotnością odejmowania. Chociaż jest własną odwrotnością dodatku ( $-0 = 0$ ), addytywna odwrotność liczby dodatniej jest ujemna, a addytywna odwrotność liczby ujemnej jest dodatnia. Podwójne zastosowanie tej operacji jest zapisane jako $-(-3) = 3$ . Znak plus jest używany głównie w algebrze do oznaczenia binarnej operacji dodawania i rzadko do podkreślenia pozytywności wyrażenia.

W powszechnym zapisie liczbowym (używanym w arytmetyce i innych miejscach) znak liczby jest często wyraźnie zaznaczany przez umieszczenie znaku plusa lub minusa przed liczbą. Na przykład $+3$ oznacza „dodatnią trójkę”, a $-3$ „ujemną trójkę” (algebraicznie: addytywna odwrotność $3$ ). Bez określonego kontekstu (lub gdy nie podano wyraźnego znaku) liczba jest domyślnie interpretowana jako dodatnia. Ten zapis ustanawia silne skojarzenie znaku minus „ $-$ " z liczbami ujemnymi, a znak plus "+" z liczbami dodatnimi.

Znak zera

$0$ $0$ $0$ $0$ Zgodnie z konwencją, że zero nie jest ani dodatnie, ani ujemne, do wartości liczbowej można przypisać określoną wartość znaku . Jest to wykorzystywane w funkcji ${\ displaystyle \ operatorname {sgn}}$ -function , jak zdefiniowano dla liczb rzeczywistych. W arytmetyce $+0$ i $-0$ oznaczają tę samą liczbę . Generalnie nie ma niebezpieczeństwa pomylenia wartości z jej znakiem, chociaż konwencja przypisania obu znaków nie pozwala od razu na to rozróżnienie.

W niektórych kontekstach, zwłaszcza w informatyce , warto rozważyć podpisane wersje zera, przy czym zera ze znakiem odnoszą się do różnych, dyskretnych reprezentacji liczb ( więcej informacji można znaleźć w podpisanych reprezentacjach liczb ).

$0$ Symbole $+0$ i $-0$ rzadko pojawiają się jako substytuty $0 +$ i $0 -$ , używane w rachunku różniczkowym i analizie matematycznej dla granic jednostronnych (odpowiednio granica prawostronna i granica lewostronna). Ten zapis odnosi się do zachowania funkcji, gdy jej rzeczywista zmienna wejściowa zbliża się wzdłuż wartości dodatnich (odpowiednio ujemnych); te dwie granice nie muszą istnieć ani się zgadzać.

Terminologia dotycząca znaków

$0$ Kiedy mówi się, że nie jest ani dodatnia, ani ujemna, następujące wyrażenia mogą odnosić się do znaku liczby:

Liczba jest dodatnia , jeśli jest większa od zera.
Liczba jest ujemna , jeśli jest mniejsza od zera.
Liczba jest nieujemna, jeśli jest większa lub równa zeru.
Liczba nie jest dodatnia, jeśli jest mniejsza lub równa zeru.

$0$ Kiedy mówi się, że jest zarówno dodatnie, jak i ujemne, w odniesieniu do znaku liczby używane są zmodyfikowane wyrażenia:

Liczba jest ściśle dodatnia, jeśli jest większa od zera.
Liczba jest ściśle ujemna, jeśli jest mniejsza od zera.
Liczba jest dodatnia , jeśli jest większa lub równa zeru.
Liczba jest ujemna , jeśli jest mniejsza lub równa zeru.

Na przykład wartość bezwzględna liczby rzeczywistej jest zawsze „nieujemna”, ale niekoniecznie „dodatnia” w pierwszej interpretacji, podczas gdy w drugiej interpretacji nazywana jest „dodatnią” - choć niekoniecznie „ściśle dodatnią” .

Ta sama terminologia jest czasami używana dla funkcji , które dają wartości rzeczywiste lub inne ze znakiem. Na przykład funkcja byłaby nazywana funkcją dodatnią , jeśli jej wartości są dodatnie dla wszystkich argumentów jej dziedziny, lub funkcją nieujemną, jeśli wszystkie jej wartości są nieujemne.

Liczby zespolone

Liczb zespolonych nie można uporządkować, więc nie mogą mieć struktury uporządkowanego pierścienia, a zatem nie można ich podzielić na dodatnie i ujemne liczby zespolone. Mają jednak wspólny atrybut z liczbami rzeczywistymi, który nazywa się wartością bezwzględną lub wielkością . Wielkości są zawsze nieujemnymi liczbami rzeczywistymi, a do każdej niezerowej liczby należy dodatnia liczba rzeczywista, jej wartość bezwzględna .

Na przykład wartość bezwzględna $-3$ i wartość bezwzględna $3$ są równe $3$ . Jest to zapisane symbolami jako $| -3 | = 3$ i $| 3 | = 3$ .

Ogólnie rzecz biorąc, dowolną wartość rzeczywistą można określić za pomocą jej wielkości i znaku. Używając standardowego kodowania, każda rzeczywista wartość jest dana przez iloczyn wielkości i znaku w standardowym kodowaniu. Relację tę można uogólnić, aby zdefiniować znak dla liczb zespolonych.

Ponieważ zarówno liczby rzeczywiste, jak i zespolone tworzą pole i zawierają dodatnie liczby rzeczywiste, zawierają również odwrotności wielkości wszystkich liczb niezerowych. Oznacza to, że dowolną liczbę różną od zera można pomnożyć przez odwrotność jej wielkości, czyli podzielić przez jej wielkość. Jest natychmiastowe, że iloraz dowolnej niezerowej liczby rzeczywistej przez jej wielkość daje dokładnie jej znak. Analogicznie znak liczby zespolonej $z$ można zdefiniować jako iloraz liczby $z$ i jej wielkości $| z |$ . Znak liczby zespolonej jest wykładniczym iloczynu jej argumentu z jednostką urojoną. reprezentuje w pewnym sensie jego złożony argument. $to$ rzeczywistych, z wyjątkiem definicji złożonej funkcji znaku patrz § Złożona funkcja znaku poniżej.

Funkcje znakowe

Funkcja znaku rzeczywistego

y = sgn(x)

Kiedy mamy do czynienia z liczbami, często wygodnie jest mieć ich znak dostępny jako liczba. Osiąga się to za pomocą funkcji, które wyodrębniają znak dowolnej liczby i odwzorowują go na predefiniowaną wartość przed udostępnieniem go do dalszych obliczeń. Na przykład korzystne może być sformułowanie skomplikowanego algorytmu tylko dla wartości dodatnich i dopiero później zajęcie się znakiem.

Funkcja znaku rzeczywistego

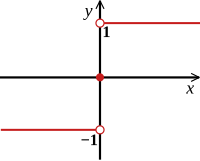
Funkcja signum lub funkcja signum wyodrębnia znak liczby rzeczywistej, odwzorowując zbiór liczb rzeczywistych na zbiór trzech liczb rzeczywistych ${\ Displaystyle \ {- 1, \; 0, \; 1 \}.}$ Można to zdefiniować w następujący sposób:

{\ Displaystyle {\ rozpocząć {wyrównane} \ nazwa operatora {sgn}: {} & \ mathbb {R} \ do \ {-1,0,1 \} \\& x \ mapsto \ nazwa operatora {sgn} (x) = { \begin{przypadki}-1&{\text{if }}x<0,\\~~\,0&{\text{if }}x=0,\\~~\,1&{\text{if }} x>0.\end{przypadki}}\end{wyrównane}}}

Zatem

sgn(x)

wynosi 1, gdy

x

jest dodatnie, a

sgn(x)

wynosi −1, gdy

x

jest ujemne. Dla niezerowych wartości

x

funkcję tę można również zdefiniować za pomocą wzoru

{\ Displaystyle \ nazwa operatora {sgn} (x) = {\ Frac {x} {| x |}} = {\ Frac {| x|} {x}},}

gdzie

| x |

jest wartością bezwzględną

x

.

Złożona funkcja znaku

Podczas gdy liczba rzeczywista ma kierunek jednowymiarowy, liczba zespolona ma kierunek dwuwymiarowy. Funkcja znaku zespolonego wymaga wielkości swojego argumentu $z = x + iy$ , którą można obliczyć jako

{\ Displaystyle | z | = {\ sqrt {z {\ bar {z}}}} = {\ sqrt {x ^ {2} + y ^ {2}}}.}

$0$ $0$ Analogicznie do powyższego, funkcja znaku zespolonego wyodrębnia znak zespolony liczby zespolonej, odwzorowując zbiór niezerowych liczb zespolonych na zbiór jednomodułowych liczb zespolonych i na : ${\ Displaystyle \ {z \ in \ mathbb {C}: | z | = 1 \} \ kubek \ {0 \}.}$ Można to zdefiniować w następujący sposób:

Niech $z$ będzie również wyrażone przez jego wielkość i jeden z jego argumentów $φ$ jako $z = | z |\cdot mi jaφ,$ więc

{\ Displaystyle \ nazwa operatora {sgn} (z) = {\ rozpocząć {przypadki} 0 i {\ tekst {dla}} z = 0 \\ {\ dfrac {z} {| z |}} = e ^ {i \ varphi }&{\text{inaczej}}.\end{przypadki}}}

Definicja ta może być również uznana za wektor znormalizowany, to znaczy wektor, którego kierunek jest niezmienny i którego długość jest ustalona na jedność . Jeśli pierwotną wartością było R,θ w postaci biegunowej, to znak (R, θ) wynosi 1 θ. Rozszerzenie funkcji sign() lub signum() na dowolną liczbę wymiarów jest oczywiste, ale zostało to już zdefiniowane jako normalizowanie wektora.

Znaki według konwencji

W sytuacjach, w których istnieją dokładnie dwie równe możliwości dla atrybutu, są one często określane umownie jako odpowiednio plus i minus . W niektórych kontekstach wybór tego przypisania (tj. który zakres wartości uznawany jest za dodatni, a który za ujemny) jest naturalny, podczas gdy w innych jest to wybór arbitralny, wymagający jawnej konwencji znakowej, której jedynym wymogiem jest konsekwentne stosowanie Konwencji.

Znak kąta

Mierząc od osi x , kąty na okręgu jednostkowym liczą się jako dodatnie w kierunku przeciwnym do ruchu wskazówek zegara i ujemne w kierunku zgodnym z ruchem wskazówek zegara .

W wielu kontekstach często kojarzy się znak z miarą kąta , zwłaszcza kąta zorientowanego lub kąta obrotu . W takiej sytuacji znak wskazuje, czy kąt jest zgodny z wskazówek zegara , czy przeciwnie do ruchu wskazówek zegara. Chociaż można stosować różne konwencje, w matematyce często kąty przeciwne do ruchu wskazówek zegara są liczone jako dodatnie, a kąty zgodne z ruchem wskazówek zegara jako ujemne.

Możliwe jest również powiązanie znaku z kątem obrotu w trzech wymiarach, przy założeniu, że oś obrotu została zorientowana. W szczególności w prawo wokół zorientowanej osi zwykle liczy się jako dodatni, podczas gdy obrót w lewo liczy się jako ujemny.

Znak zmiany

Gdy wielkość x zmienia się w czasie, zmiana wartości x jest zwykle definiowana przez równanie

{\ Displaystyle \ Delta x = x _ {\ tekst {końcowy}} -x_ {\ tekst {początkowy}}.}

Stosując tę konwencję, wzrost x liczy się jako zmiana dodatnia, podczas gdy spadek x liczy się jako zmiana ujemna. W rachunku różniczkowym ta sama konwencja jest używana w definicji pochodnej . W rezultacie każda rosnąca funkcja ma pochodną dodatnią, podczas gdy każda funkcja malejąca ma pochodną ujemną.

Znak kierunku

W geometrii analitycznej i fizyce często określa się pewne kierunki jako dodatnie lub ujemne. Dla podstawowego przykładu, oś liczbowa jest zwykle rysowana z liczbami dodatnimi po prawej stronie i liczbami ujemnymi po lewej stronie:

W rezultacie, podczas omawiania ruchu liniowego , przemieszczenia lub prędkości , ruch w prawo jest zwykle uważany za dodatni, podczas gdy podobny ruch w lewo jest uważany za ujemny.

Na płaszczyźnie kartezjańskiej kierunki w prawo i w górę są zwykle uważane za dodatnie, przy czym kierunek w prawo jest dodatnim kierunkiem x , a kierunek w górę jest dodatnim kierunkiem y . Jeśli wektor przemieszczenia lub prędkości zostanie rozdzielony na składowe wektora , wówczas część pozioma będzie dodatnia dla ruchu w prawo i ujemna dla ruchu w lewo, podczas gdy część pionowa będzie dodatnia dla ruchu w górę i ujemna dla ruchu w dół.

Sygnalizacja w informatyce

Najbardziej znaczący bit
0	1	1	1	1	1	1	1	=	127
0	1	1	1	1	1	1	0	=	126
0	0	0	0	0	0	1	0	=	2
0	0	0	0	0	0	0	1	=	1
0	0	0	0	0	0	0	0	=	0
1	1	1	1	1	1	1	1	=	−1
1	1	1	1	1	1	1	0	=	−2
1	0	0	0	0	0	0	1	=	−127
1	0	0	0	0	0	0	0	=	−128
Większość komputerów używa dopełnienia do dwóch do przedstawienia znaku liczby całkowitej.

W obliczeniach wartość całkowita może być albo ze znakiem, albo bez znaku, w zależności od tego, czy komputer śledzi znak liczby. Ograniczając zmienną całkowitą tylko do wartości nieujemnych, można użyć jeszcze jednego bitu do przechowywania wartości liczby. Ze względu na sposób, w jaki arytmetyka liczb całkowitych jest wykonywana w komputerach, reprezentacje liczb ze znakiem zwykle nie przechowują znaku jako pojedynczego niezależnego bitu, zamiast tego używają np. uzupełnienia do dwóch .

Natomiast liczby rzeczywiste są przechowywane i przetwarzane jako wartości zmiennoprzecinkowe . Wartości zmiennoprzecinkowe są reprezentowane za pomocą trzech oddzielnych wartości: mantysy, wykładnika i znaku. Biorąc pod uwagę ten oddzielny bit znaku, możliwe jest reprezentowanie zarówno dodatniego, jak i ujemnego zera. Większość języków programowania zwykle traktuje dodatnie zero i ujemne zero jako wartości równoważne, chociaż zapewniają one środki, za pomocą których można wykryć rozróżnienie.

Inne znaczenia

Ładunek elektryczny może być dodatni lub ujemny.

Oprócz znaku liczby rzeczywistej znak słowny jest również używany na różne powiązane sposoby w matematyce i innych naukach:

Słowa do znaku oznaczają, że dla wielkości $q$ wiadomo, że albo $q = Q$ , albo $q = - Q$ dla pewnego $Q$ . Często jest wyrażany jako $q = \pm Q$ . Dla liczb rzeczywistych oznacza to, że tylko wartość bezwzględna $| q |$ znana jest ilość W przypadku liczb zespolonych i wektorów wielkość znana do znaku jest silniejszym warunkiem niż wielkość ze znanym wielkość : oprócz $Q$ i $- Q$ , istnieje wiele innych możliwych wartości $q$ takich, że $| q | = | P |$ .
Znak permutacji jest definiowany jako dodatni, jeśli permutacja jest parzysta, i ujemny, jeśli permutacja jest nieparzysta.
W teorii grafów graf ze znakiem to graf, w którym każda krawędź została oznaczona znakiem dodatnim lub ujemnym.
W analizie matematycznej miara ze znakiem jest uogólnieniem pojęcia miary , w którym miara zbioru może mieć wartości dodatnie lub ujemne.
W reprezentacji cyfr ze znakiem każda cyfra liczby może mieć znak dodatni lub ujemny.
Idee podpisanego obszaru i podpisanej objętości są czasami używane, gdy dla niektórych obszarów lub objętości jest wygodne liczenie jako ujemne. Jest to szczególnie prawdziwe w teorii uwarunkowań . W (abstrakcyjnie) zorientowanej przestrzeni wektorowej każdą uporządkowaną podstawę przestrzeni wektorowej można sklasyfikować jako zorientowaną dodatnio lub ujemnie.
W fizyce każdy ładunek elektryczny ma znak, dodatni lub ujemny. Zgodnie z konwencją, ładunek dodatni to ładunek o tym samym znaku co proton , a ładunek ujemny to ładunek o tym samym znaku co elektron .

Zobacz też

^. ^ ^abc ^Weisstein , Eric W. „ Znak” mathworld.wolfram.com . Źródło 2020-08-26 .
Bibliografia _ _ www.cs.cas.cz . Źródło 2020-08-26 .
^ „Znak kątów | Co to jest kąt? | Kąt dodatni | Kąt ujemny” . Matematyka Tylko matematyka . Źródło 2020-08-26 .

[:0-1] . ^ ^abc ^Weisstein , Eric W. „ Znak” mathworld.wolfram.com . Źródło 2020-08-26 .

[2] Bibliografia _ _ www.cs.cas.cz . Źródło 2020-08-26 .

[3] „Znak kątów | Co to jest kąt? | Kąt dodatni | Kąt ujemny” . Matematyka Tylko matematyka . Źródło 2020-08-26 .