Dowody małego twierdzenia Fermata

W tym artykule zebrano różne dowody małego twierdzenia Fermata , które to stwierdza

${\ Displaystyle a ^ {p} \ równoważnik a {\ pmod {p}}}$

dla każdej liczby pierwszej p i każdej liczby całkowitej a (patrz arytmetyka modularna ).

uproszczenia

Niektóre z podanych poniżej dowodów małego twierdzenia Fermata opierają się na dwóch uproszczeniach.

Po pierwsze, możemy założyć, że a mieści się w przedziale 0 ≤ a ≤ p − 1 . Jest to prosta konsekwencja praw arytmetyki modularnej ; mówimy po prostu, że możemy najpierw zredukować modulo p . Jest to zgodne z redukcją $modulo$ jak można sprawdzić .

Po drugie, wystarczy to udowodnić

${\ Displaystyle a ^ {p-1} \ równoważnik 1 {\ pmod {p}}}$

dla za w przedziale 1 ≤ za ≤ p - 1 . Rzeczywiście, jeśli poprzednie twierdzenie dotyczy takiego , pomnożenie obu stron przez a daje pierwotną postać twierdzenia,

${\ Displaystyle a ^ {p} \ równoważnik a {\ pmod {p}}}$

Z drugiej strony, jeśli a = 0 lub a = 1 , twierdzenie jest trywialne.

Dowody kombinatoryczne

Dowód przez liczenie naszyjników

Jest to prawdopodobnie najprostszy znany dowód, wymagający najmniejszego zaplecza matematycznego. Jest to atrakcyjny przykład dowodu kombinatorycznego (dowód polegający na liczeniu zbioru przedmiotów na dwa różne sposoby ).

Podany tutaj dowód jest adaptacją dowodu Golomba .

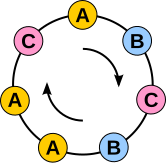
Dla uproszczenia załóżmy, że a jest dodatnią liczbą całkowitą . Rozważ wszystkie możliwe ciągi p symboli , używając alfabetu z różnymi symbolami. Całkowita liczba takich ciągów wynosi p ^reguła , ponieważ istnieje możliwość dla każdej z p pozycji (patrz iloczynu ).

Na przykład, jeśli p = 5 i a = 2 , to możemy użyć alfabetu z dwoma symbolami (powiedzmy A i B ), i mamy 2 ⁵ = 32 łańcuchy o długości 5:

AAAAA , AAAAB , AAABA , AAABB , AABAA , AABAB , AABBA , AABBB ,

ABAAA , ABAAB , ABABA , ABABB , ABBAA , ABBAB , ABBBA , ABBBB ,

BAAAA , BAAAB , BAABA , BAABB , BABAA , BABAB , BABBA , BABBB ,

BBAAA , BBAAB , BBABA , BBABB , BBBAA , BBBAB , BBBBA , BBBBB .

Poniżej wykażemy, że jeśli usuniemy z listy ciągi składające się z pojedynczego symbolu (w naszym przykładzie AAAAA i BBBBB ), pozostałe ciągi a ^p − a można ułożyć w grupy, z których każda zawiera dokładnie p ciągów. Wynika z tego, że a ^p − a jest podzielne przez p .

Naszyjniki

Naszyjnik przedstawiający siedem różnych napisów ( ABCBAAC , BCBAACA , CBAACAB , BAACABC , AACABCB , ACABCBA , CABCBAA )

Naszyjnik przedstawiający tylko jeden sznurek ( AAAAAAA )

Pomyślmy o każdym takim sznurku jako o naszyjniku . Oznacza to, że łączymy ze sobą dwa końce sznurka i traktujemy dwa sznurki jako ten sam naszyjnik, jeśli możemy obrócić jeden sznurek, aby uzyskać drugi sznurek; w tym przypadku powiemy, że te dwa ciągi są przyjaciółmi . W naszym przykładzie wszystkie następujące łańcuchy są przyjaciółmi:

AAAAB , AAABA , AABAA , ABAAA , BAAAA .

W całości, każdy wiersz poniższej listy odpowiada pojedynczemu naszyjnikowi, a cała lista zawiera wszystkie 32 struny.

AAAAB , AAABA , AABAA , ABAAA , BAAAA ,

AAABB , AABBA , ABBAA , BBAAA , BAAAB ,

AABAB , ABABA , BABAA , ABAAB , BAABA ,

AABBB , ABBBA , BBBAA , BBAAB , BAABB ,

ABABB , BABBA , ABBAB , BBABA , BABAB ,

ABBBB , BBBBA , BBBAB , BBABB , BABBB ,

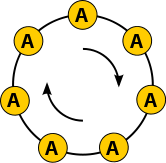
AAAAA ,

BBBBB .

Zauważ, że na powyższej liście każdy naszyjnik z więcej niż jednym symbolem jest reprezentowany przez 5 różnych sznurków, a liczba naszyjników reprezentowanych przez tylko jeden sznurek wynosi 2, tj. jest liczbą odrębnych symboli. Zatem lista pokazuje bardzo wyraźnie, dlaczego 32 − 2 jest podzielne przez 5 .

Można skorzystać z następującej reguły, aby obliczyć, ilu przyjaciół ma dany ciąg S :

Jeśli S jest zbudowane z kilku kopii ciągu T , a samego T nie można dalej podzielić na powtarzające się ciągi, to liczba przyjaciół S (w tym samego S ) jest równa długości T .

Załóżmy na przykład, że zaczynamy od ciągu S = ABBABBABBABB , który składa się z kilku kopii krótszego ciągu T = ABB . Jeśli obrócimy go o jeden symbol na raz, otrzymamy następujące 3 ciągi:

ABBABBABBABB ,

BBABBABBABBA ,

BABBABBABBAB .

Nie ma żadnych innych, ponieważ ABB ma dokładnie 3 symbole i nie można go podzielić na dalsze powtarzające się ciągi.

Uzupełnienie dowodu

Korzystając z powyższej reguły, możemy dość łatwo zakończyć dowód małego twierdzenia Fermata w następujący sposób. Naszą początkową pulę łańcuchów ^p można podzielić na dwie kategorie:

• Niektóre łańcuchy zawierają p identycznych symboli. Jest ich dokładnie jeden , po jednym dla każdego symbolu w alfabecie. (W naszym działającym przykładzie są to łańcuchy znaków AAAAA i BBBBB .)
• Reszta ciągów używa co najmniej dwóch różnych symboli z alfabetu. Jeśli możemy rozbić S na powtarzające się kopie jakiegoś łańcucha T , długość T musi być podzielona przez długość S . Ale ponieważ długość S jest liczbą pierwszą p , jedyną możliwą długością T jest również p . Dlatego powyższa reguła mówi nam, że S ma dokładnie p przyjaciół (wliczając w to samego S ).

Druga kategoria zawiera struny ^p − jednej a i można je ułożyć w grupy p strun, po grupie dla każdego naszyjnika. Dlatego a ^p − a musi być podzielne przez p , zgodnie z obietnicą.

Dowód za pomocą układów dynamicznych

Dowód ten wykorzystuje kilka podstawowych pojęć z układów dynamicznych .

Zaczynamy od rozważenia rodziny funkcji T _n ( x ), gdzie n ≥ 2 jest liczbą całkowitą , odwzorowując przedział [0, 1] na siebie za pomocą wzoru

${\ Displaystyle T_ {n} (x) = {\ rozpocząć {przypadki} \ {nx \} i 0 \ równoważnik x <1, \\1&x=1,\end{przypadki}}}$

gdzie { y } oznacza część ułamkową y . Na przykład funkcja T ₃ ( x ) jest zilustrowana poniżej:

₀₀₀₀ liczba x jest punktem stałym funkcji f ( x ), jeśli f ( x ) = x ; innymi słowy, jeśli f pozostawia x stałe. Punkty stałe funkcji można łatwo znaleźć graficznie: są to po prostu x punktów, w których wykres funkcji f ( x ) przecina wykres linii y = x . Na przykład stałymi punktami funkcji T ₃ ( x ) są 0, 1/2 i 1; zaznaczono je czarnymi kółkami na poniższym schemacie:

Będziemy potrzebować następujących dwóch lematów.

Lemat 1. Dla dowolnego n ≥ 2 funkcja T _n ( x ) ma dokładnie n punktów stałych.

Dowód. Na powyższej ilustracji są 3 stałe punkty i ten sam argument geometryczny dotyczy każdego n ≥ 2.

Lemat 2. Dla dowolnych dodatnich liczb całkowitych n i m oraz dowolnych 0 ≤ x ≤ 1,

${\ Displaystyle T_ {m} (T_ {n} (x)) = T_ {mn} (x).}$

Innymi słowy _, Tmn ( x ) jest złożeniem Tn ( x ) i Tm ₍ x ) _.

Dowód. Dowód tego lematu nie jest trudny, ale musimy być nieco ostrożni z punktem końcowym x = 1. W tym punkcie lemat jest oczywiście prawdziwy, ponieważ

${\ Displaystyle T_ {m} (T_ {n} (1)) = T_ {m} (1) = 1 = T_ {mn} (1).}$

Załóżmy więc, że 0 ≤ x < 1. W tym przypadku

${\ Displaystyle T_ {n} (x) = \ {nx \ <1,}$

więc T _m ( T _n ( x )) jest dane przez

${\ Displaystyle T_ {m} (T_ {n} (x)) = \ {m \ {nx \} \}.}$

Dlatego tak naprawdę musimy to pokazać

${\ Displaystyle \ {m \ {nx \} \} = \ {mnx \}.}$

W tym celu obserwujemy, że { nx } = nx − k , gdzie k jest częścią całkowitą liczby nx ; Następnie

${\ Displaystyle \ {m \ {nx \} \} = \ {mnx-mk \} = \ {mnx \} ,}$

ponieważ mk jest liczbą całkowitą.

Teraz właściwie rozpocznijmy dowód małego twierdzenia Fermata od zbadania funkcji T _{a ^p} ( x ). Założymy, że ^a ≥ 2. Z Lematu 1 wiemy, że ma p punktów stałych. Z Lematu 2 wiemy, że

${\ Displaystyle T_ {a ^ {p}} (x) = \ underbrace {T_ {a} (T_ {a}(\cdots T_{a}(x)\cdots ))} _{p{\text{razy}}},}$

więc każdy stały punkt T _a ( x ) jest automatycznie stałym punktem T _{a ^p} ( x ).

Interesują nas punkty stałe T _{a ^p} ( x ), które nie są stałymi punktami T _a ( x ). Nazwijmy zbiór takich punktów S . Istnieje p − ^a punktów w S , ponieważ znowu z Lematu 1 T _a ( x ) ma dokładnie stałe punkty. Poniższy diagram ilustruje sytuację dla a = 3 i p = 2. Czarne kółka to punkty S , których jest 3 ² − 3 = 6.

₀ Główną ideą dowodu jest teraz podzielenie zbioru S up na jego orbity pod T _a . Oznacza to, że wybieramy punkt x w S i wielokrotnie stosujemy do niego T _a (x), aby otrzymać sekwencję punktów

${\ Displaystyle x_ {0}, T_ {a} (x_ {0}), T_ {a} (T_ {a} (x_ {0})), T_ {a} (T_ {a} (T_ {a} (x_{0}))),\ldkropki .}$

₀ Sekwencja ta nazywana jest orbitą x pod T _a . Zgodnie z Lematem 2 sekwencję tę można zapisać jako

${\ Displaystyle x_ {0}, T_ {a} (x_ {0}), T_ {a ^ {2}} (x_ {0}), T_ {a ^ {3}} (x_ {0}), \ kropki .}$

₀₀₀ Ponieważ zakładamy, że x jest stałym punktem T _{a ^p} ( x ), po p krokach uderzamy w T _{a ^p} ( x ) = x i od tego momentu sekwencja się powtarza.

₀ Jednak sekwencja nie może zacząć się powtarzać wcześniej. Gdyby tak było, długość powtarzającej się sekcji musiałaby być dzielnikiem p , więc musiałaby wynosić 1 (ponieważ p jest liczbą pierwszą). Jest to jednak sprzeczne z naszym założeniem, że x nie jest stałym punktem T _a .

Innymi słowy, orbita zawiera dokładnie p różnych punktów. Dotyczy to każdej orbity S . Dlatego zbiór S , który zawiera p - a punktów, można podzielić na orbity, z których każda zawiera p punktów , więc a ^p - a jest podzielne przez p ^.

(Ten dowód jest zasadniczo taki sam, jak dowód liczenia naszyjników podany powyżej, po prostu widziany przez inną soczewkę: można pomyśleć o przedziale [0, 1] jako określonym przez sekwencje cyfr o podstawie a (nasze rozróżnienie między 0 a 1 odpowiada znanemu rozróżnieniu między przedstawianiem liczb całkowitych jako kończących się na „.0000…” i „.9999…”). T _{a ⁿ} jest równoznaczne z przesunięciem takiej sekwencji o n wiele cyfr. Stałymi punktami tego będą sekwencje które są cykliczne z okresem dzielącym n . W szczególności stałe punkty T _{a ^p} można traktować jako naszyjniki o długości p , przy czym T _{a ⁿ} odpowiada rotacji takich naszyjników o n miejsc.

Dowód ten można również przedstawić bez rozróżnienia między 0 a 1, po prostu używając przedziału półotwartego [0, 1); wtedy T _n miałoby tylko n − 1 punktów stałych, ale T _{a ^p} − T _a nadal wychodziłoby na a ^p − a , w razie potrzeby.)

Dowody wielomianowe

Dowód 1

Dowód ten, ze względu na Eulera , wykorzystuje indukcję do udowodnienia twierdzenia dla wszystkich liczb całkowitych a ≥ 0 .

Krok podstawowy, że 0 ^p ≡ 0 (mod p ) , jest trywialny. Następnie musimy pokazać, że jeśli twierdzenie jest prawdziwe dla a = k , to jest również prawdziwe dla a = k + 1 . Dla tego kroku indukcyjnego potrzebujemy następującego lematu.

Lemat . Dla dowolnych liczb całkowitych x i y oraz dla dowolnej liczby pierwszej p , ( x + y ) ^p ≡ x ^p + y ^p (mod p ) .

Lemat jest przypadkiem snu pierwszoroczniaka . Zostawiając dowód na później, przechodzimy do indukcji.

dowód . Załóżmy k ^p ≡ k (mod p ) i rozważmy ( k +1) ^p . Zgodnie z lematem, który mamy

${\ Displaystyle (k + 1) ^ {p} \ równoważnik k ^ {p} + 1 ^ {p} {\ pmod {p}}.}$

Korzystając z hipotezy indukcji, mamy, że k ^p ≡ k (mod p ); i, trywialnie, 1 ^p = 1. Zatem

${\ Displaystyle (k + 1) ^ {p} \ równoważnik k + 1 {\ pmod {p}},}$

co jest stwierdzeniem twierdzenia dla a = k +1. ∎

Aby udowodnić lemat, musimy wprowadzić twierdzenie dwumianowe , które mówi, że dla dowolnej dodatniej liczby całkowitej n ,

${\ Displaystyle (x + y) ^ {n} = \ suma _ {i = 0} ^ {n} {n \ wybierz i}x^{ni}y^{i},}$

gdzie współczynniki są współczynnikami dwumianowymi ,

$\ Displaystyle {n \ wybierz i} = {\ Frac {n!} {i! (ni)!}}}$

opisane za pomocą funkcji silni , n ! = 1×2×3×⋯× n .

Dowód lematu. Rozważamy współczynnik dwumianowy, gdy wykładnik jest liczbą pierwszą p :

${\ Displaystyle {p \ wybierz i} = {\ Frac {p!} {i! (pi)!}}}$

Wszystkie współczynniki dwumianowe są liczbami całkowitymi. Licznik zawiera czynnik p zgodnie z definicją silni. Gdy 0 < i < p , żaden z wyrazów w mianowniku nie zawiera czynnika p (opierając się na pierwszorzędności p ), pozostawiając sam współczynnik posiadający czynnik pierwszy p z licznika, co sugeruje, że

${\ Displaystyle {p \ wybierz i} \ równoważnik 0 {\ pmod {p}}, \ qquad 0 <i <p.}$

Modulo p , to eliminuje wszystkie oprócz pierwszego i ostatniego wyrazu sumy po prawej stronie twierdzenia dwumianowego dla liczby pierwszej p . ∎

Pierwszość p jest niezbędna dla lematu; w przeciwnym razie mamy przykłady takie jak

${\ Displaystyle {4 \ wybierz 2} = 6,}$

co nie jest podzielne przez 4.

Dowód 2

Korzystając z lematu mamy:

${\ Displaystyle k ^ {p} \ równoważnik ((k-1) + 1) ^ {p} \ równoważnik (k-1) ^ {p} + 1 \ równoważnik ((k-2) + 1) ^ {p }+1\equiv (k-2)^{p}+2\equiv \dots \equiv k{\pmod {p}}}$ .

Dowód za pomocą rozwinięcia wielomianowego

Dowód, który został po raz pierwszy odkryty przez Leibniza (który go nie opublikował), a później ponownie odkryty przez Eulera , jest bardzo prostym zastosowaniem twierdzenia o wielomianach , które stwierdza

${\ Displaystyle (x_ {1} + x_ {2} + \ cdots + x_ {m}) ^ {n} = \ suma _ {k_ {1}, k_ {2} ,\kropki ,k_{m} \na górze k_{1}+k_{2}+\kropki +k_{m}=n}{n \wybierz k_{1},k_{2},\ldots ,k_{m }}x_{1}^{k_{1}}x_{2}^{k_{2}}\cdots x_{m}^{k_{m}}}$

Gdzie

${\ Displaystyle {n \ wybierz k_ {1}, k_ {2}, \ ldots, k_ {m}} = {\ Frac {n!} {k_ {1}! k_ {2}! \ kropki k_ {m} !}}}$

a sumowanie obejmuje wszystkie ciągi nieujemnych indeksów całkowitych ki _k 1 _, k 2 _, ..., k _m takie, że suma wszystkich wynosi n .

Zatem jeśli wyrazimy a jako sumę jedynek, otrzymamy

${\ Displaystyle a ^ {p} = (1 + 1 +... + 1) ^ {p} = \ suma _ {k_ {1}, k_ {2}, \ kropki, k_ {a} \ na szczycie k_ { 1}+k_{2}+\kropki +k_{a}=p}{p \wybierz k_{1},k_{2},\ldots ,k_{a}}}$

Oczywiście, jeśli p jest liczbą pierwszą i jeśli kj _nie jest równe p dla dowolnego j , mamy

${\ Displaystyle {p \ wybierz k_ {1}, k_ {2}, \ ldots, k_ {a}} \ równoważnik 0 {\ pmod {P}},}$

a jeśli k _j jest równe p dla pewnego j, to wtedy

${\ Displaystyle {p \ wybierz k_ {1}, k_ {2}, \ ldots, k_ {a}} = 1.}$

Ponieważ istnieją dokładnie takie elementy , że k _j = p dla pewnego j , wynika z tego twierdzenie.

(Ten dowód jest w zasadzie bardziej gruboziarnistym wariantem dowodu liczenia naszyjników podanego wcześniej; współczynniki wielomianowe liczą, na ile sposobów łańcuch może zostać permutowany w dowolne anagramy, podczas gdy argument naszyjnik liczy, ile sposobów można obrócić sznurek na cykliczne anagramy. To znaczy, że nietrywialne współczynniki wielomianowe tutaj są podzielne przez p , można postrzegać jako konsekwencję faktu, że każdy nietrywialny naszyjnik o długości p można rozwinąć w sznurek na wiele sposobów.

To wielomianowe rozwinięcie jest również, oczywiście, tym, co zasadniczo leży u podstaw powyższego dowodu opartego na twierdzeniu o dwumianach )

Dowód za pomocą rozszerzeń produktów mocy

Dowód addytywno-kombinatoryczny oparty na formalnych rozwinięciach iloczynów mocy przedstawił Giedrius Alkauskas. Dowód ten nie wykorzystuje ani algorytmu euklidesowego , ani twierdzenia dwumianowego , ale raczej wykorzystuje formalne szeregi potęgowe z wymiernymi współczynnikami.

Dowód jako szczególny przypadek twierdzenia Eulera

Dowód ten, odkryty przez Jamesa Ivory'ego i ponownie odkryty przez Dirichleta , wymaga pewnej wiedzy z zakresu arytmetyki modułowej .

Załóżmy, że a jest dodatnie i niepodzielne przez p . Chodzi o to, że jeśli zapiszemy sekwencję liczb

${\ Displaystyle a, 2a, 3a, \ ldots, (p-1) a}$

 

 

 

 

()

i zredukować każdy modulo p , wynikowa sekwencja okazuje się być przegrupowaniem

${\ Displaystyle 1,2,3, \ ldots, p-1.}$

 

 

 

 

()

Dlatego jeśli pomnożymy razem liczby w każdej sekwencji, wyniki muszą być identyczne modulo p :

${\ Displaystyle a \ razy 2a \ razy 3a \ razy \ cdots \ razy (p-1) a \ równoważnik 1 \ razy 2 \ razy 3 \ razy \ cdots \ razy (p-1) {\ pmod {p}}. }$

Zbieranie razem daje warunki

${\ Displaystyle a ^ {p-1} (p-1)! \ równoważnik (p-1)! {\ pmod {p}}.}$

Ostatecznie możemy „skreślić” liczby 1, 2, ..., p − 1 z obu stron tego równania, otrzymując

${\ Displaystyle a ^ {p-1} \ równoważnik 1 {\ pmod {p}}.}$

W powyższym dowodzie są dwa kroki, które musimy uzasadnić:

• Dlaczego elementy ciągu ( A ), zredukowane modulo p , są przegrupowaniem ( B ) i
• Dlaczego „anulowanie” jest ważne w przypadku arytmetyki modularnej.

Poniżej udowodnimy te rzeczy; zobaczmy najpierw przykład tego dowodu w działaniu.

Przykład

Jeśli a = 3 i p = 7 , to rozważana sekwencja to

${\ Displaystyle 3,6,9,12,15,18;}$

redukcja modulo 7 daje

${\ Displaystyle 3,6,2,5,1,4,}$

co jest tylko przeróbką

${\ Displaystyle 1,2,3,4,5,6.}$

Pomnożenie ich razem daje

${\ Displaystyle 3 \ razy 6 \ razy 9 \ razy 12 \ razy 15 \ razy 18 \ równoważnik 3 \ razy 6 \ razy 2 \ razy 5 \ razy 1 \ razy 4 \ odpowiednik 1 \ razy 2 \ razy 3 \ razy 4 \ razy 5\razy 6{\pmod {7}};}$

to jest,

${\ Displaystyle 3 ^ {6} (1 \ razy 2 \ razy 3 \ razy 4 \ razy 5 \ razy 6) \ równoważnik (1 \ razy 2 \ razy 3 \ razy 4 \ razy 5 \ razy 6) {\ pmod { 7}}.}$

Anulowanie 1 × 2 × 3 × 4 × 5 × 6 daje plony

${\ Displaystyle 3 ^ {6} \ równoważnik 1 {\ pmod {7}},}$

co jest małym twierdzeniem Fermata dla przypadku a = 3 i p = 7 .

Prawo anulowania

Wyjaśnijmy najpierw, dlaczego w pewnych sytuacjach „anulowanie” jest ważne. Dokładne stwierdzenie jest następujące. Jeśli u , x i y są liczbami całkowitymi, a u nie jest podzielne przez liczbę pierwszą p i jeśli

${\ Displaystyle ux \ równoważnik uy {\ pmod {p}},}$

 

 

 

 

()

wtedy możemy „anulować” u , aby uzyskać

${\ displaystyle x \ równoważnik y {\ pmod {p}}.}$

 

 

 

 

()

Nasze użycie tego prawa anulowania w powyższym dowodzie małego twierdzenia Fermata było poprawne, ponieważ liczby 1, 2, ..., p − 1 z pewnością nie są podzielne przez p (w rzeczywistości są mniejsze niż p ).

Możemy łatwo udowodnić prawo anulowania, korzystając z lematu Euklidesa , który ogólnie mówi, że jeśli liczba pierwsza p dzieli iloczyn ab (gdzie a i b są liczbami całkowitymi), to p musi dzielić a lub b . Rzeczywiście, twierdzenie ( C ) oznacza po prostu, że p dzieli ux − uy = u ( x − y ) . od str jest liczbą pierwszą, która nie dzieli u , lemat Euklidesa mówi nam, że zamiast tego musi dzielić x − y ; to znaczy ( D ) zachodzi.

Należy zauważyć, że warunki, w których obowiązuje prawo anulowania, są dość ścisłe i to wyjaśnia, dlaczego małe twierdzenie Fermata wymaga, aby p było liczbą pierwszą. Na przykład 2×2 ≡ 2×5 (mod 6) , ale nie jest prawdą, że 2 ≡ 5 (mod 6) . Jednakże obowiązuje następujące uogólnienie prawa anulowania: jeśli u , x , y i z są liczbami całkowitymi, jeśli u i z są względnie pierwsze i jeśli

${\ Displaystyle ux \ równoważnik uy {\ pmod {z}},}$

wtedy możemy „anulować” u , aby uzyskać

${\ displaystyle x \ równoważnik y {\ pmod {z}}.}$

Wynika to z uogólnienia lematu Euklidesa .

Właściwość przegrupowania

Na koniec musimy wyjaśnić, dlaczego sekwencja

${\ Displaystyle a, 2a, 3a, \ ldots, (p-1) a,}$

po zredukowaniu modulo p staje się przegrupowaniem sekwencji

${\ Displaystyle 1,2,3, \ ldots, p-1.}$

Zacznijmy od tego, że żaden z wyrazów a , 2 a , ..., ( p − 1) a nie może być przystający do zera modulo p , ponieważ jeśli k jest jedną z liczb 1, 2, ..., p − 1 , to k jest względnie pierwsze z p , podobnie jak a , więc lemat Euklidesa mówi nam, że ka nie ma wspólnego dzielnika z p . Dlatego przynajmniej wiemy, że liczby a , 2 a , ..., ( p − 1) a , zredukowane modulo p , musi znaleźć się wśród liczb 1, 2, 3, ..., p − 1 .

Ponadto liczby a , 2 a , ..., ( p − 1) a muszą być różne po ich skróceniu modulo p , ponieważ jeśli

${\ Displaystyle ka \ równoważnik ma {\ pmod {p}},}$

gdzie k i m są jednym z 1, 2, ..., p − 1 , to prawo anulowania mówi nam, że

${\ displaystyle k \ równoważnik m {\ pmod {p}}.}$

Ponieważ oba k i m są między 1 a p - 1 , muszą być równe. Dlatego wyrazy a , 2 a , ..., ( p − 1) a zredukowane modulo p muszą być różne. Podsumowując: kiedy zmniejszymy liczby p − 1 a , 2 a , ..., ( p − 1) a modulo p , otrzymujemy różne wyrazy ciągu 1 , 2 , ..., p − 1 . Ponieważ jest ich dokładnie p - 1 , jedyną możliwością jest to, że te pierwsze są przegrupowaniem tych drugich.

Zastosowania do twierdzenia Eulera

Tej metody można również użyć do udowodnienia twierdzenia Eulera , z niewielką zmianą polegającą na tym, że liczby od 1 do p - 1 są zastępowane przez liczby mniejsze niż i względnie pierwsze z pewną liczbą m (niekoniecznie pierwszą). Zarówno właściwość przegrupowania, jak i prawo anulowania (w uogólnionej formie wspomnianej powyżej ) są nadal spełnione i można je wykorzystać.

Na przykład, jeśli m = 10 , to liczbami mniejszymi niż m i względnie pierwszymi z m są 1 , 3 , 7 i 9 . Mamy więc:

${\ Displaystyle a \ razy 3a \ razy 7a \ razy 9a \ równoważnik 1 \ razy 3 \ razy 7 \ razy 9 {\ pmod {10}}.}$

Dlatego,

${\ Displaystyle {a ^ {\ varphi (10)}} \ równoważnik 1 {\ pmod {10}}.}$

Dowód jako następstwo kryterium Eulera

Główny artykuł: kryterium Eulera § Alternatywny dowód

Dowody z wykorzystaniem teorii grup

Standardowy dowód

Dowód ten wymaga najbardziej podstawowych elementów teorii grup .

Chodzi o to, aby uznać, że zbiór G = {1, 2, …, p − 1 }, z operacją mnożenia (biorąc modulo p ), tworzy grupę . Jedynym aksjomatem grupowym, którego sprawdzenie wymaga pewnego wysiłku, jest to, że każdy element G jest odwracalny. Biorąc to na wiarę, załóżmy, że a mieści się w przedziale 1 ≤ a ≤ p − 1 , czyli a jest elementem G . Niech k będzie porządkiem z a , to znaczy k jest najmniejszą dodatnią liczbą całkowitą taką, że a ^k ≡ 1 (mod p ) . Wtedy liczby 1, a , a ² , ..., a ^{k −1} zredukowane modulo p tworzą podgrupę G , której rząd wynosi k , a zatem, zgodnie z twierdzeniem Lagrange'a , k dzieli rząd G , który wynosi p - 1 . Zatem p − 1 = km dla pewnej dodatniej liczby całkowitej m a następnie

${\ Displaystyle a ^ {p-1} \ równoważnik a ^ {km} \ równoważnik (a ^ {k}) ^ {m} \ równoważnik 1 ^ {m} \ równoważnik 1 {\ pmod {p}}.}$

Aby udowodnić, że każdy element b z G jest odwracalny, możemy postępować w następujący sposób. Po pierwsze, b jest względnie pierwsze z p . Zatem tożsamość Bézouta zapewnia nas, że istnieją liczby całkowite x i y takie, że bx + py = 1 . Czytając tę ​​równość modulo p , widzimy, że x jest odwrotnością dla b , ponieważ bx ≡ 1 (mod p ) . Dlatego każdy element G jest odwracalny. Tak więc, jak wspomniano wcześniej, G jest grupą.

Na przykład, gdy p = 11 , odwrotności każdego elementu są podane w następujący sposób:

A	1	2	3	4	5	6	7	8	9	10
a -1	1	6	4	3	9	2	8	7	5	10

Dowód Eulera

Jeśli weźmiemy poprzedni dowód i zamiast twierdzenia Lagrange'a spróbujemy go udowodnić w tej konkretnej sytuacji, to otrzymamy trzeci dowód Eulera, który uznał za bardziej naturalny. Niech A będzie zbiorem, którego elementami są liczby 1, a , a ² , ..., a ^{k − 1} zredukowane modulo p . Jeśli A = G , to k = p - 1 , a zatem k dzieli p -1 . W przeciwnym razie jest jakieś b ₁ ∈ G \ A .

Niech A ₁ będzie zbiorem, którego elementami są liczby b ₁ , ab ₁ , a ² b ₁ , …, a ^{k − 1} b ₁ zredukowane modulo p . Wtedy A ₁ ma k różnych elementów, bo inaczej byłyby dwie różne liczby m , n ∈ {0, 1, ..., k − 1 } takie, że a ^m b ₁ ≡ a ⁿ b ₁ (mod p ) , co jest niemożliwe, ponieważ wynikałoby z tego, że a ^m ≡ a ⁿ (mod p ) . Z drugiej strony żaden element zbioru A _{1 nie} może być elementem zbioru A , ponieważ w przeciwnym razie istniałyby liczby m , n ∈ {0, 1, …, k − 1 } takie, że a ^m b ₁ ≡ a ⁿ (mod p ) , a następnie b ₁ ≡ za ⁿ za ^{k - m} ≡ za ^{n + k - m} (mod p ) , co jest niemożliwe, ponieważ b ₁ ∉ ZA .

Zatem zbiór A ∪ A ₁ ma 2 k elementów. Jeśli okaże się, że jest równe G , to 2 k = p −1 , a zatem k dzieli p −1 . W przeciwnym razie jest jakieś b ₂ ∈ G \( A ∪ A ₁ ) i możemy zacząć wszystko od nowa, definiując A ₂ jako zbiór, którego elementami są liczby b ₂ , ab ₂ , za ² b ₂ , ..., za ^{k - 1} b ₂ zredukowane modulo p . Ponieważ G jest skończone, proces ten musi się w pewnym momencie zatrzymać, a to dowodzi, że k dzieli p − 1 .

Na przykład, jeśli a = 5 i p = 13 , to od

• 5 ² = 25 ≡ 12 (mod 13) ,
• 5 ³ = 125 ≡ 8 (mod 13) ,
• 5 ⁴ = 625 ≡ 1 (mod 13) ,

mamy k = 4 i A = {1, 5, 8, 12 }. Oczywiście A ≠ G = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} . Niech b ₁ będzie elementem G \ A ; na przykład weźmy b ₁ = 2 . Wtedy, od

• 2×1 = 2 ,
• 2×5 = 10 ,
• 2×8 = 16 ≡ 3 (mod 13) ,
• 2×12 = 24 ≡ 11 (mod 13) ,

mamy A ₁ = {2, 3, 10, 11 }. Oczywiście, ZA ∪ ZA ₁ ≠ G . Niech b ₂ będzie elementem G \( A ∪ A ₁ ) ; na przykład weźmy b ₂ = 4 . Wtedy, od

• 4×1 = 4 ,
• 4×5 = 20 ≡ 7 (mod 13) ,
• 4×8 = 32 ≡ 6 (mod 13) ,
• 4×12 = 48 ≡ 9 (mod 13) ,

mamy A ₂ = {4, 6, 7, 9 }. A teraz G = ZA ∪ ZA ₁ ∪ ZA ₂ .

Zauważ, że zbiory A , A ₁ itd. są w rzeczywistości cosetami zbioru A w G .