Pseudojednorodny wielościan
Pseudojednorodny tę wielościan to wielościan , który ma wielokąty foremne jako ściany i ma samą konfigurację wierzchołków na wszystkich wierzchołkach , ale nie jest przechodni przez wierzchołki : nie jest prawdą, że dla dowolnych dwóch wierzchołków istnieje symetria wielościanu odwzorowującego pierwszy izometrycznie na drugą. Zatem chociaż wszystkie wierzchołki pseudojednorodnego wielościanu wyglądają tak samo, nie jest on izogonalny . Nazywa się je pseudojednorodnymi wielościanami ze względu na ich podobieństwo do prawdziwych jednolitych wielościanów .
Istnieją dwa pseudojednorodne wielościany: pseudorombikubooktaedr i pseudo-wielki rombikubooktaedr . Obydwa mają D 4d , taką samą jak antygraniastosłup kwadratowy . Obydwa można zbudować z jednolitego wielościanu , przekręcając jedną czapkę w kształcie kopuły.
Pseudojednorodne wielościany
Pseudorhombikubooktaedr
Pseudorombukoboktahedr jest jedynym wypukłym pseudojednostajnym wielościanem. Jest to również bryła Johnsona (J 37 ) i można ją również nazwać wydłużoną kwadratową żyrobikupią . Jego dualnością jest dwudziestościan pseudodeltoidalny . Jak sama nazwa wskazuje, można ją skonstruować poprzez wydłużenie kwadratowej żyrobikupoli ( J 29 ) i wstawienie ośmiokątnego pryzmatu pomiędzy jego dwiema połówkami. Powstała bryła jest lokalnie wierzchołkowo-regularna — układ czterech ścian padających na dowolny wierzchołek jest taki sam dla wszystkich wierzchołków; jest to wyjątkowe wśród ciał stałych Johnsona. Nie jest to jednak przechodnia wierzchołków , a co za tym idzie, nie jest to jedna z brył Archimedesa , ponieważ istnieją pary wierzchołków takie, że nie ma izometrii bryły, która odwzorowuje jeden na drugi. Zasadniczo te dwa typy wierzchołków można rozróżnić na podstawie ich „sąsiadów sąsiadów”. Innym sposobem sprawdzenia, czy wielościan nie jest regularny z wierzchołkami, jest zauważenie, że wokół jego równika znajduje się dokładnie jeden pas ośmiu kwadratów, co odróżnia wierzchołki pasa od wierzchołków po obu stronach.
 Rombuboktaedr |
 Rozbite sekcje |
 Pseudo-rombikuboktaedr |
Bryłę można również zobaczyć w wyniku skręcenia jednej z kwadratowych kopuł ( J 4 ) na rombowo-sześciennym ośmiościanie (jednej z brył Archimedesa ; inaczej wydłużonej kwadratowej ortobicupoli) o 45 stopni. Jego podobieństwo do rombowo-sześciennego ośmiościanu nadaje mu alternatywną nazwę pseudorhombicuboctahedron . Czasami nazywano ją „czternastą bryłą Archimedesa”.
W przypadku ścian pokolorowanych według symetrii D 4d może to wyglądać następująco:
| pseudorombikubooktaedr |
Dwuścian pseudonaramienny Dwuścian wielościanowy |
|
|---|---|---|
 internet |

|

|
równika znajduje się 8 (zielonych) kwadratów , 4 (czerwone) trójkąty i 4 (żółte) kwadraty powyżej i poniżej oraz jeden (niebieski) kwadrat na każdym biegunie.
Budowę jednolitych i pseudo rombowo-sześciennych można zobaczyć w następujących powiększeniach ośmiokątnego pryzmatu:
 Pryzmat ośmiokątny (kolorowy o symetrii D 8h )... |
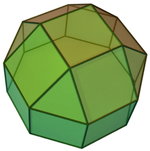 ...z jednym z ośmiokątów powiększonym kwadratową kopułą. |
 Istnieją dwie możliwości orientacji drugiej nieskrzyżowanej kwadratowej kopuły. Wyrównuje się odpowiednie ściany (trójkąty z trójkątami, kwadraty z kwadratami) i powstaje rombowo-ośmiościan. Konstrukcja ta ma D 4h , chociaż rombowo-sześcienny ośmiościan ma pełną symetrię oktaedryczną. |
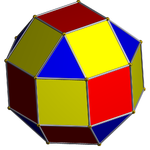 Drugi wybór wyrównuje nieodpowiednie ściany (trójkąty z kwadratami) i tworzy pseudorombicubośmiościan . Konstrukcja ta ma D 4d . |
Pseudowielki ośmiościan rombowy
Jednolity , niewypukły wielki rombowo-sześcian ośmiościan może być postrzegany jako oktagramowy pryzmat z oktagramami wydrążonymi ze skrzyżowanymi kwadratowymi kopułami, podobnie jak rombowo- sześcienny ośmiościan może być postrzegany jako ośmiokątny pryzmat z ośmiokątami powiększonymi kwadratowymi kopułami. Obracanie jednej z kopuł w tej konstrukcji skutkuje pseudowielkim rombikubośmiościanem .
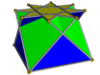 Skrzyżowana kwadratowa kopuła |
 Niewypukły wielki ośmiościan rombowy |
 Pseudowielki ośmiościan rombowy |
Poniższe zdjęcia przedstawiają wykopy w pryzmacie oktagramowym ze skrzyżowanymi kwadratowymi kopułami, etapami. Skrzyżowane kwadratowe kopuły są zawsze czerwone, natomiast kwadratowe boki pryzmatu oktagramowego są w pozostałych kolorach. Dla przejrzystości wszystkie obrazy są zorientowane w przybliżeniu w ten sam sposób.
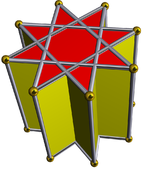 Pryzmat oktagramowy (kolorowy o symetrii D 8h )... |
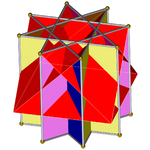 ...z jednym z oktagramów (tutaj górny) wydobytym ze skrzyżowaną kwadratową kopułą. Można to nazwać wydłużoną, skrzyżowaną kwadratową kopułą lub powiększonym pryzmatem oktagramowym i jest izomorficzna z wydłużoną kwadratową kopułą Johnsona . |
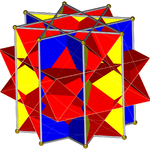 Istnieją dwie możliwości orientacji drugiej skrzyżowanej kwadratowej kopuły. Wyrównuje się odpowiednie ściany (trójkąty z trójkątami, kwadraty z kwadratami) i tworzy się niewypukły wielki rombowo-ośmiościan. Konstrukcja ta ma D 4h , chociaż niewypukły wielki ośmiościan rombowy ma pełną symetrię oktaedryczną . |
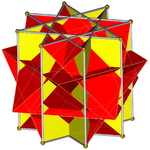 Drugi wybór wyrównuje nieodpowiednie ściany (trójkąty z kwadratami) i tworzy pseudo-wielki rombikubooktaedr (lub pseudokwazirohombikubośmiościan). Konstrukcja ta ma D 4d . |
Pseudowielki ośmiościan rombowo-sześcienny ma pojedynczy „pas” kwadratów wokół równika i można go skonstruować, skręcając jedną ze skrzyżowanych kopuł kwadratowych na niewypukłym ośmiościanie wielkim rombowo-sześciennym o 45 stopni. Jest to analogiczne do pseudorombikubooktaedru.
Podwójne pseudojednorodne wielościany
Wszystkie twarze dualne pseudojednorodnych wielościanów są przystające , ale nie przechodnie: nie wszystkie ich ściany leżą na tej samej orbicie symetrii , a zatem nie są izoedryczne . Jest to konsekwencja pseudojednorodnych wielościanów mających tę samą konfigurację wierzchołków w każdym wierzchołku, ale nie będących przechodnimi przez wierzchołki . Świadczą o tym różne kolory użyte do twarzy na obrazach podwójnych pseudojednorodnych wielościanów w tym artykule, oznaczających różne typy twarzy.

