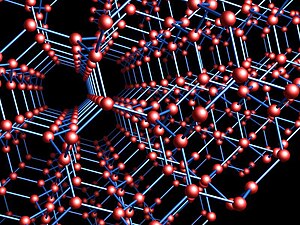
Wykres Lavesa

W geometrii i krystalografii wykres Lavesa to nieskończony i wysoce symetryczny układ punktów i odcinków w trójwymiarowej przestrzeni euklidesowej , tworzący wykres okresowy . Trzy segmenty o równej długości spotykają się pod kątem 120° w każdym punkcie, a wszystkie cykle wykorzystują dziesięć lub więcej segmentów. Jest to najkrótszy możliwy wykres potrójnie okresowy w stosunku do objętości jego dziedziny podstawowej . Jeden układ wykresu Lavesa wykorzystuje jeden z każdych ośmiu punktów w siatce liczb całkowitych jako jego punkty i łączy wszystkie pary tych punktów, które są najbliższymi sąsiadami , w odległości ${\ displaystyle {\ sqrt {2}}}$ . Można go również zdefiniować, w oderwaniu od jego geometrii, jako abstrakcyjny graf nieskierowany , graf obejmujący cały graf na czterech wierzchołkach.

HSM Coxeter ( 1955 ) nazwał kryształem K4 _ten graf na cześć Fritza Lavesa , który po raz pierwszy napisał o nim jako o strukturze krystalicznej w 1932 roku. Nazywano go również , (10,3)-sieć , diamentowy bliźniak , triamond i srs netto . Regiony przestrzeni najbliższe każdemu wierzchołkowi wykresu to przystające 17-boczne wielościany, które są kafelkami przestrzeni. Jego krawędzie leżą na przekątnych regularnego skośnego wielościanu , powierzchnia z sześcioma kwadratami spotykającymi się w każdym całkowitym punkcie przestrzeni.

Kilka krystalicznych substancji chemicznych ma znane lub przewidywane struktury w postaci wykresu Lavesa. Pogrubienie krawędzi wykresu Lavesa do cylindrów daje powiązaną minimalną powierzchnię , gyroid , który fizycznie pojawia się w niektórych strukturach filmu mydlanego i skrzydłach motyli.

Konstrukcje

Z siatki liczb całkowitych

Regularny wielościan skośny , w który można wpisać wykres Lavesa. Krawędzie wykresu Lavesa są przekątnymi niektórych kwadratów tej wielościennej powierzchni.

Jak opisuje Coxeter (1955) , wierzchołki grafu Lavesa można zdefiniować, wybierając jeden z każdych ośmiu punktów trójwymiarowej sieci liczb całkowitych i tworząc graf najbliższego sąsiada . W szczególności wybiera się punkty

{\ Displaystyle {\ rozpocząć {wyrównane} (0,0,0), \ quad (1,2,3), \ quad (2,3,1), \ quad (3,1,2) ),\\(2,2,2),\quad (3,0,1),\quad (0,1,3),\quad (1,3,0),\\\koniec {wyrównane}} }

i wszystkie inne punkty utworzone przez dodanie wielokrotności czterech do tych współrzędnych. Krawędzie wykresu Lavesa łączą pary punktów, których odległość euklidesowa od siebie jest pierwiastkiem kwadratowym z dwóch , ponieważ punkty każdej pary różnią się o jedną jednostkę w dwóch współrzędnych,

{\ Displaystyle {\ sqrt {2}}}

i są takie same w trzeciej współrzędnej. Krawędzie stykają się pod kątem 120° w każdym wierzchołku na płaskiej płaszczyźnie. Wszystkie pary wierzchołków, które nie sąsiadują ze sobą, są dalej od siebie, w odległości co najmniej

{\ displaystyle {\ sqrt {6}}}

od siebie. Krawędzie powstałego graf geometryczny to przekątne podzbioru ścian regularnego wielościanu skośnego z sześcioma kwadratowymi ścianami na wierzchołek, więc wykres Lavesa jest osadzony w tym skośnym wielościanie.

Możliwe jest wybranie większego zestawu jednego na cztery punkty siatki całkowitej, tak aby wykres par odległości $większego$ zestawu tworzył dwie lustrzane kopie wykresu Lavesa, odłączonych od siebie, ze wszystkimi innymi parami punktów dalej niż ${\ displaystyle {\ sqrt {2}}}$ od siebie.

Jako wykres pokrywający

$wykres$ Lavesa można skonstruować jako maksymalny abelowy wykres pokrywający wykresu . Bycie abelowym grafem pokrywającym $}$ mogą być czterokolorowe, tak że każdy wierzchołek ma sąsiadów z pozostałych trzech kolorów i tak, że istnieją symetrie zachowujące kolor K 4 {\ displaystyle K_ dowolnego wierzchołka do dowolnego innego wierzchołka o tym samym kolorze. Dla wykresu Lavesa w jego postaci geometrycznej ze współrzędnymi całkowitymi, te symetrie są translacje , które dodają liczby parzyste do każdej współrzędnej (dodatkowo przesunięcia wszystkich trzech współrzędnych muszą być zgodne modulo cztery). Stosując kolejno dwa takie tłumaczenia, translacja netto jest niezależna od ich kolejności: dojeżdżają one do siebie, tworząc grupę abelową . Wektory translacji z tej grupy tworzą trójwymiarową siatkę . Wreszcie bycie wykresem pokrywającym maksymalnego abela oznacza, że nie ma innego wykresu pokrywającego ${\ displaystyle K_ {4}}$ z udziałem sieci o wyższych wymiarach. Ta konstrukcja $kryształu$ alternatywną nazwę wykresu Lavesa .

Wykres maksymalnego pokrycia abelowego można skonstruować z dowolnego wykresu skończonego ${\ displaystyle G}$ ; zastosowana do , konstrukcja tworzy (abstrakcyjny) wykres Lavesa, ale nie nadaje mu tego samego $układu$ Wybierz drzewo rozpinające , niech $będzie$ liczbą krawędzi, których nie ma w drzewie rozpinającym (w tym przypadku trzy krawędzie niebędące drzewami) i $wybierz$ wektor w ${\ displaystyle \ mathbb {Z} ^ {d}}$ dla każdej z tych niebędących drzewami krawędzi. Następnie $Displaystyle$ zbiór wierzchołków wykresu pokrywającego tak, aby były to $\ displaystyle w}$ $pary$ $,$ gdzie jest $}$ jest wektorem w ${\ displaystyle \ mathbb {Z} ^ {d}}$ . Dla $każdej$ takiej pary i każdej do ${\ Displaystyle v}$ w ${\ Displaystyle G}$ , zrób krawędź od ${\ Displaystyle (v, w)}$ do $}$ ${\ Displaystyle (u, w \ pm \ epsilon$ $)$ gdzie jest $zerowym,$ ${\ displaystyle uv}$ należy drzewa opinającego, a poza tym jest wektorem bazowym powiązanym z , i gdzie znak plus lub minus jest wybierany w zależności od kierunku, w którym krawędź jest przemierzana. Otrzymany wykres jest niezależny od wybranego drzewa rozpinającego, a tę samą konstrukcję można również interpretować bardziej abstrakcyjnie za pomocą homologii .

Używając tej samej konstrukcji, sześciokątne nakładanie płaszczyzny jest wykresem maksymalnego pokrycia abelowego trójkrawędziowego dipola , a sześcienny romb jest maksymalnym wykresem pokrycia abelowego dipola czterokrawędziowego. D ${\ displaystyle d} -wymiarowa siatka całkowita (jako wykres$ $z$ krawędziami o jednostkowej długości) jest maksymalnym abelowym wykresem obejmującym wykres z jednym wierzchołkiem własnymi .

Jako wykres odległości jednostkowej

Wykres jednostkowej odległości na trójwymiarowej siatce liczb całkowitych ma wierzchołek dla każdego punktu sieci; każdy wierzchołek ma dokładnie sześciu sąsiadów. Możliwe jest usunięcie niektórych punktów z sieci, tak aby każdy pozostały punkt miał dokładnie trzech pozostałych sąsiadów, a indukowany podwykres tych punktów nie miał cykli krótszych niż dziesięć krawędzi. Można to zrobić na cztery sposoby, z których jeden jest izomorficzny jako wykres abstrakcyjny z wykresem Lavesa. Jednak jego wierzchołki znajdują się w innych pozycjach niż w bardziej symetrycznej, konwencjonalnej konstrukcji geometrycznej.

Nieruchomości

Graf Lavesa jest grafem sześciennym , co oznacza, że w każdym wierzchołku są dokładnie trzy krawędzie. Każdą parę wierzchołka i sąsiedniej krawędzi można przekształcić w każdą inną taką parę przez symetrię grafu, więc jest to graf symetryczny . Silniej, dla każdych dwóch wierzchołków $każdej$ korespondencji jeden do jednego między trzema krawędziami incydentnymi z trzema krawędziami incydentnymi z $u}$ $displaystyle$ ${\ displaystyle v} v}$ można zrealizować za pomocą symetrii. Jednak ogólna struktura jest chiralna : żadna sekwencja translacji i obrotów nie może sprawić, że zbiegnie się ona z jej lustrzanym odbiciem.

Obwód tej struktury wynosi 10 — najkrótsze cykle w grafie mają 10 wierzchołków — a 15 z tych cykli przechodzi przez każdy wierzchołek . Liczby wierzchołków w odległości 0, 1, 2, ... od dowolnego wierzchołka (tworzące sekwencję koordynacyjną grafu Lavesa) to:

1, 3, 6, 12, 24, 35, 48, 69, 86, 108, 138, 161, 192, 231, ... (sekwencja A038620 w OEIS ) .

Komórki diagramu Woronoja wykresu Lavesa

Jeśli otaczająca przestrzeń jest podzielona na regiony najbliższe każdemu wierzchołkowi - komórki diagramu Woronoja tej struktury - tworzą one heptadekaedrę z 17 ścianami każda. Są to plezjoedry , wielościany, które układają przestrzeń w izoedry . Eksperymenty ze strukturami tworzonymi przez te wielościany doprowadziły fizyka Alana Schoena do odkrycia minimalnej powierzchni żyroskopu , która jest topologicznie równoważna powierzchni uzyskanej przez pogrubienie krawędzi wykresu Lavesa do walców i przejęcie granicy ich związku.

Graf Lavesa jest unikalną najkrótszą siecią potrójnie okresową w następującym sensie. Potrójnie okresowa oznacza powtarzanie się w nieskończoność we wszystkich trzech wymiarach przestrzeni, więc sieć potrójnie okresowa jest połączonym wykresem geometrycznym z trójwymiarową siatką translacyjnych symetrii. Podstawową domeną jest dowolny kształt, który może układać przestrzeń ze swoimi przetłumaczonymi kopiami pod tymi symetriami. Każda $ma$ nieskończenie wiele możliwości wyboru domeny podstawowej o różnych kształtach, ale wszystkie mają tę samą objętość . Można również zmierzyć długość krawędzi sieci w obrębie pojedynczej kopii domeny podstawowej; Zadzwoń pod ten numer ${\ displaystyle L}$ . Podobnie jak w $,$ nie zależy od wyboru domeny podstawowej, o ile granica domeny przecina tylko krawędzie, a nie zawiera części ich $.$ Graf Lavesa ma cztery klasy symetrii wierzchołków ( orbit ), ponieważ rozważane tutaj symetrie to tylko translacje, a nie obroty potrzebne do odwzorowania tych czterech klas na siebie. Każda klasa symetrii ma jeden wierzchołek w dowolnej dziedzinie podstawowej, więc dziedzina podstawowa zawiera dwanaście półkrawędzi o łącznej długości ${\ Displaystyle 6 {\ sqrt {2}}}$ . $} 2}}}$ 32. Z tych dwóch liczb stosunek ( wielkość bezwymiarowa ) wynosi zatem ${\ Displaystyle L ^ {3}/V$ . Jest to w rzeczywistości minimalna możliwa wartość: wszystkie sieci potrójnie okresowe mają

{\ Displaystyle {\ Frac {L ^ {3}} {V}} \ geq {\ Frac {27} {\ sqrt {2}}}}

z równością tylko w przypadku wykresu Lavesa.

Przykłady fizyczne

Model 3D części wykresu Lavesa

Sztuka

Rzeźba zatytułowana Bamboozle autorstwa Jacobusa Verhoeffa i jego syna Toma Verhoeffa ma postać fragmentu wykresu Lavesa, którego wierzchołki są reprezentowane przez wielokolorowe, zazębiające się trójkąty akrylowe. Został zainstalowany w 2013 roku na Politechnice w Eindhoven .

Kryształy molekularne

Wykres Lavesa został zasugerowany jako alotrop węgla , analogiczny do bardziej powszechnej struktury węgla grafenu i grafitu , które również mają trzy wiązania na atom pod kątem 120 °. W grafenie sąsiednie atomy mają takie same płaszczyzny wiązania, podczas gdy w strukturze grafu Lavesa płaszczyzny wiązania sąsiednich atomów są skręcone o kąt około 70,5° wokół linii wiązania. Jednak ten hipotetyczny alotrop węgla okazuje się niestabilny.

Wykres Lavesa może również dać strukturę krystaliczną boru , która według obliczeń powinna być stabilna. Inne substancje chemiczne, które mogą tworzyć tę strukturę, to SrSi ₂ (od którego wywodzi się nazwa „srs net”) i azot elementarny , a także niektóre struktury metaloorganiczne i węglowodory cykliczne .

Zbadano strukturę pasm elektronowych dla modelu ciasnego wiązania grafu Lavesa, wykazując istnienie punktów Diraca i Weyla w tej strukturze.

Inny

Strukturę wykresu Lavesa i wywodzących się z niego powierzchni żyroskopowych zaobserwowano również eksperymentalnie w układach mydło-woda oraz w sieciach chitynowych łusek skrzydeł motyla .

Linki zewnętrzne

Hart, George W. , Sieć (10, 3) .
Sloane, NJA (red.), „Sekwencja A046944 (liczba unikających się spacerów o długości n na wykresie Lavesa)” , The On-Line Encyclopedia of Integer Sequences , Fundacja OEIS
Sloane, NJA (red.), „Sekwencja A290705 (seria Theta triamond)” , The On-Line Encyclopedia of Integer Sequences , Fundacja OEIS