D 6 polytope
 6-sześcian |
 6-ortopleks |
geometrii 6-wymiarowej istnieje 47 jednolitych polytopów o symetrii D 6 , z których 16 jest unikalnych, a 31 jest wspólnych z symetrią B 6 . Istnieją dwie regularne formy, 6-ortopleks i 6-półsześcian z odpowiednio 12 i 32 wierzchołkami.
Można je wizualizować jako symetryczne projekcje ortograficzne w płaszczyznach Coxetera grupy D6 Coxetera i innych podgrup.
Wykresy
Symetryczne rzuty prostokątne tych 16 polytopów można wykonać w płaszczyznach D 6 , D 5 , D 4 , D 3 , A 5 , A 3 , Coxeter . A k ma symetrię [k+1] , D k ma symetrię [2(k-1)] . B 6 jest również uwzględnione, chociaż w tych polytopach istnieje tylko połowa jego [12] symetrii.
Każdy z tych 16 polytopów jest pokazany na tych 7 płaszczyznach symetrii, z narysowanymi wierzchołkami i krawędziami oraz wierzchołkami pokolorowanymi według liczby nakładających się wierzchołków w każdej pozycji rzutowej.
| # | Wykresy płaszczyzny Coxetera |
Diagram Coxetera Nazwy |
||||||
|---|---|---|---|---|---|---|---|---|
|
B6 [ 12/2] |
D 6 [10] |
D 5 [8] |
D 4 [6] |
re 3 [4] |
5 [ 6] |
3 [4 ] |
||
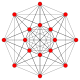
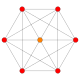
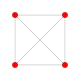
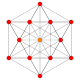
| 1 |  |
 |
 |
 |
 |
 |
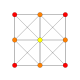 |
= 6-półsześcian Hemihexeract (hax) |
| 2 |  |
 |
 |
 |
 |
 |
 |
= kantyczny 6-sześcian Ścięty hemihexeract ( thax ) |
| 3 |  |
 |
 |
 |
 |
 |
 |
= Runcic 6-cube Mały rombowy hemihexeract (sirhax) |
| 4 |  |
 |
 |
 |
 |
 |
 |
= steryczny 6-sześcian Mały pryzmat hemihekserakt (sofaks) |
| 5 |  |
 |
 |
 |
 |
 |
 |
= pentic 6-cube Mały komórkowy demihekserakt ( sochax ) |
| 6 |  |
 |
 |
 |
 |
 |
 |
= runcicantic 6-cube Wielki rombowy hemihexeract ( girhax ) |
| 7 |  |
 |
 |
 |
 |
 |
 |
= stericantic 6-sześcian prismatościęty hemihexeract (pithax) |
| 8 |  |
 |
 |
 |
 |
 |
 |
= steriruncic 6-cube Prismatorhombated hemihexeract ( prohax ) |
| 9 |  |
 |
 |
 |
 |
 |
 |
= Stericantic 6-sześcian Cellitruncated hemihexeract (cathix) |
| 10 |  |
 |
 |
 |
 |
 |
 |
= Pentiruncic 6-sześcian Cellirhombated hemihexeract (crohax) |
| 11 |  |
 |
 |
 |
 |
 |
 |
= Pentysteryczny 6-sześcianowy hemihexeract z pryzmatem komórkowym (cophix) |
| 12 |  |
 |
 |
 |
 |
 |
 |
= Steriruncicantic 6-sześcian Wielki pryzmatyczny hemihexeract (gophax) |
| 13 |  |
 |
 |
 |
 |
 |
 |
= Pentiruncicantic 6-sześcian Celligreatorhombated hemihexeract (cagrohax) |
| 14 |  |
 |
 |
 |
 |
 |
 |
= Pentisstericantic 6-cube Celliprismato ścięty hemihexeract (capthix) |
| 15 |  |
 |
 |
 |
 |
 |
 |
= Pentisteriruncic 6-sześcian Celliprismatorhombated hemihexeract (caprohax) |
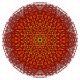
| 16 |  |
 |
 |
 |
 |
 |
 |
= Pentisteriruncicantic 6-sześcian Wielki hemihekserakt komórkowy (gochax) |
-
HSM Coxeter :
- HSM Coxeter, Regular Polytopes , wydanie 3, Dover, Nowy Jork, 1973
-
Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Papier 22) HSM Coxeter, Regularne i półregularne Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Papier 23) HSM Coxeter, Regularne i półregularne Polytopes II , [Math. Zeit. 188 (1985) 559-591]
- (Papier 24) HSM Coxeter, Regularne i półregularne Polytopy III , [Math. Zeit. 200 (1988) 3-45]
- NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Rozprawa, University of Toronto, 1966
- Klitzing, Richard. „Jednolite polytopy 6D (polipeta)” .