Efekt akustyczno-sprężysty

Efekt akustosprężysty polega na tym, jak zmieniają się prędkości dźwięku (zarówno prędkości wzdłużne , jak i prędkości fali ścinającej ) elastycznego materiału , jeśli zostanie poddany początkowemu polu naprężeń statycznych . Jest to nieliniowy efekt konstytutywnej relacji między naprężeniem mechanicznym a skończonym odkształceniem w materiale o ciągłej masie . W klasycznej liniowej teorii sprężystości małe odkształcenia większości materiałów sprężystych można opisać liniową zależnością między przyłożonym naprężeniem a wypadkowym odkształceniem. Zależność ta jest powszechnie znana jako uogólnione prawo Hooke'a . Liniowa teoria sprężystości obejmuje stałe sprężystości drugiego rzędu $($ np . $i daje stałe wzdłużne i ścinające prędkości$ dźwięku w elastycznym materiale, na które nie ma wpływu przyłożone naprężenie. Z drugiej strony efekt akustosprężysty obejmuje rozszerzenie konstytutywnej relacji (nieliniowa teoria sprężystości) wyższego rzędu między przyłożonym naprężeniem a wynikającym z niego odkształceniem, co daje prędkości dźwięku wzdłużnego i ścinającego zależne od stanu naprężenia materiału. W granicach materiału nienaprężonego odtwarzane są prędkości dźwięku z liniowej teorii sprężystości.

Efekt akustyczno-sprężysty został zbadany już w 1925 roku przez Brillouina. Odkrył, że prędkość rozchodzenia się fal akustycznych zmniejsza się proporcjonalnie do przyłożonego ciśnienia hydrostatycznego. Jednak konsekwencją jego teorii było to, że fale dźwiękowe przestałyby się rozchodzić przy wystarczająco dużym ciśnieniu. Później wykazano, że ten paradoksalny efekt był spowodowany błędnymi założeniami, że ciśnienie nie ma wpływu na parametry sprężystości.

W 1937 roku Francis Dominic Murnaghan przedstawił teorię matematyczną rozszerzającą liniową teorię sprężystości, aby obejmowała również skończone odkształcenie w elastycznych materiałach izotropowych . Teoria ta obejmowała trzy $,$ sprężystości trzeciego rzędu i m $\$$displaystyle n$ . W 1953 roku Huges i Kelly wykorzystali teorię Murnaghana w swojej pracy eksperymentalnej do ustalenia wartości liczbowych stałych sprężystości wyższego rzędu dla kilku elastycznych materiałów, w tym polistyrenu , żelaza Armco i pyreksu , poddanych ciśnieniu hydrostatycznemu i jednoosiowemu ściskaniu .

Nieliniowa teoria sprężystości dla materiałów hipersprężystych

Efekt akustosprężysty jest efektem skończonej deformacji nieliniowych materiałów sprężystych. Współczesne obszerne ujęcie tego można znaleźć w. Ta książka dotyczy zastosowania nieliniowej teorii sprężystości i analizy właściwości mechanicznych materiałów stałych zdolnych do dużych odkształceń sprężystych. Szczególny przypadek teorii akustosprężystości dla ściśliwego izotropowego materiału hiperelastycznego , takiego jak stal polikrystaliczna , został odtworzony i pokazany w tym tekście na podstawie nieliniowej teorii sprężystości przedstawionej przez Ogdena.

Należy zauważyć , że ustawienie w tym tekście, jak również w, jest izotermiczne i nie ma odniesienia do termodynamiki .

Relacja konstytutywna – materiały hipersprężyste (relacja naprężenie-odkształcenie)

Materiał hipersprężysty jest szczególnym przypadkiem materiału sprężystego Cauchy'ego , w którym naprężenie w dowolnym punkcie jest obiektywne i określone jedynie przez aktualny stan odkształcenia w odniesieniu do dowolnej konfiguracji odniesienia (więcej szczegółów na temat odkształcenia można znaleźć również na stronach Odkształcenie (mechanika ) i odkształcenie skończone ). Jednak praca wykonana przez naprężenia może zależeć od ścieżki, jaką obiera deformacja. Dlatego materiał elastyczny Cauchy'ego ma strukturę niezachowawczą, a naprężenia nie można wyprowadzić ze skalarnej potencjału sprężystego . Szczególny przypadek materiałów elastycznych Cauchy'ego, w których praca wykonywana przez naprężenia jest niezależna od ścieżki odkształcenia, nazywany jest materiałem sprężystym Greena lub materiałem hipersprężystym. Takie materiały są konserwatywne, a naprężenia w materiale można wyprowadzić ze skalarnego potencjału sprężystości, bardziej znanego jako funkcja gęstości energii odkształcenia .

Konstytutywny związek między naprężeniem a odkształceniem można wyrazić w różnych formach w oparciu o wybrane formy naprężenia i odkształcenia. Wybór pierwszego tensora naprężenia Pioli-Kirchhoffa ${$ który jest transpozycją nominalnego tensora naprężenia $\boldsymbol {N}}}$${\ Displaystyle {\ boldsymbol {P}} ^ {T} =$ ), równanie konstytutywne dla ściśliwego materiału hiperelastycznego można wyrazić za pomocą odkształcenia zieleni Lagrange'a ( ) jako: ${\ displaystyle {\ boldsymbol {E}}}$

$${\ Displaystyle {\ boldsymbol {P}} = {\ boldsymbol {F} }\cdot {\frac {\częściowy W}{\częściowy {\boldsymbol {E}}}}\qquad {\text{or}}\qquad P_{ij}=F_{ik}~{\frac {\częściowy W}{\częściowe E_{kj}}},\qquad i,j=1,2,3~,}$$

gdzie jest tensorem gradientu deformacji i gdzie drugie wyrażenie wykorzystuje konwencję $sumowania$ Einsteina zapisu indeksowego tensorów . $,$ funkcją gęstości energii odkształcenia dla materiału hiperelastycznego i została zdefiniowana na jednostkę objętości a nie na jednostkę masy, ponieważ pozwala to uniknąć konieczności mnożenia prawej strony przez gęstość masy ${\ displaystyle \ rho _ {0}}$ konfiguracji referencyjnej.

Zakładając, że skalarna funkcja gęstości energii odkształcenia $szeregu$ być przybliżona przez rozwinięcie Taylora w bieżącym odkształceniu mi $\ boldsymbol {E}}}$ , można to wyrazić (w notacji indeksowej) jako:

$${\ Displaystyle W \ około C_ {0} + C_ {ij} E_ {ij} + {\ Frac {1} {2!}$$

Nałożenie ograniczeń, że funkcja energii odkształcenia powinna wynosić zero i mieć minimum, gdy materiał jest w stanie nieodkształconym (tj. ${\ Displaystyle W (E_ {ij} = 0) = 0}$ ) jasne jest, że w funkcji energii odkształcenia nie ma stałego ani liniowego składnika, a zatem:

$${\ Displaystyle W \ około {\ Frac {1} {2!}} C_ {ijkl} E_ {ij} E_ {kl} + { \frac {1}{3!}}C_{ijklmn}E_{ij}E_{kl}E_{mn}+\cdots ,}$$

gdzie jest tensorem $jest$ modułów sprężystości drugiego rzędu podczas gdy $Displaystyle C_ {ijklmn}}$ szóstego rzędu moduły sprężystości trzeciego rzędu. Symetria wraz ze skalarną $\ displaystyle C_{ijkl}}$$odkształcenia$$implikuje$ moduły mają następującą symetrię:

$${\ Displaystyle C_ {ijkl} = C_ {jikl} = C_ {ijlk},}$$

co zmniejsza liczbę niezależnych stałych sprężystości z 81 do 36. Ponadto ekspansja mocy oznacza, że ​​​​moduły drugiego rzędu również mają większą symetrię

$${\ Displaystyle C_ {ijkl} = C_ {klij},}$$

${ijklmn}}$ dodatkowo zmniejsza liczbę niezależnych stałych sprężystości do 21. Tych samych argumentów można użyć dla modułów sprężystości trzeciego rzędu do ja jot k l . Te ${\ Displaystyle C_ {ijklmn} = C_ {IJK}})$ pozwalają również na wyrażenie modułów sprężystości za pomocą notacji Voigta (tj. do ${IJ}}$ do .

Tensor gradientu deformacji można wyrazić w postaci składowej jako

$${\ Displaystyle F_ {ij} = {\ Frac {\ częściowe u_ {i}} {\ częściowe X_ {j}}} + \ delta _ {ij} ,}$$

gdzie $}$ przemieszczeniem punktu materialnego od współrzędnej ${\ Displaystyle X_$$i}}$ w konfiguracji odniesienia do współrzędnej $}}$$\ displaystyle x_ {i$ w zdeformowanej konfiguracji (patrz rysunek 2 na stronie teorii odkształceń skończonych). Uwzględnienie rozwinięcia mocy funkcji energii $odkształcenia$ w relacji konstytutywnej i zastąpienie tensora odkształcenia Lagrange'a na stronie tensora odkształcenia skończonego (zauważ, że małe litery $\ displaystyle u }$ zostały użyte w tej sekcji w porównaniu z dużymi literami na stronie odkształcenia skończonego ) równanie konstytutywne

$${\ Displaystyle P_ {ij} = C_ {ijkl} {\ Frac {\ częściowe u_ {k}}} {\ częściowe X_ {l} }}+{\frac {1}{2}}M_{ijklmn}{\frac {\częściowe u_{k}}{\częściowe X_{l}}}{\frac {\częściowe u_{m}}{\ częściowe X_{n}}}+{\frac {1}{3}}M_{ijklmnpq}{\frac {\częściowe u_{k}}{\częściowe X_{l}}}{\frac {\częściowe u_{ m}}{\częściowe X_{n}}}{\frac {\częściowe u_{p}}{\częściowe X_{q}}}+\cdots ,}$$

Gdzie

$${\ Displaystyle M_$$

a terminy wyższego rzędu zostały zaniedbane (patrz szczegółowe wyprowadzenia). Dla odniesienia $to$ przez zaniedbywanie terminów ${\ Displaystyle P_ {ij} = C_ {ijkl} {\ Frac {\ częściowe u_ {k}} {\ częściowe X_ {l}}}}, które jest wersją uogólnionego prawa Hooke'a,$ redukuje gdzie $P_ {ij}}$${ \$$częściowe X_ {$ jest miarą stresu, podczas gdy $}}$ , a do to liniowa zależność między nimi.

Prędkość dźwięku

Zakładając, że małe odkształcenie dynamiczne (akustyczne) zaburza już obciążony statycznie materiał, efekt akustosprężysty można uznać za efekt nałożony na małe odkształcenie na większe skończone odkształcenie (zwane także teorią małych na dużych). Zdefiniujmy trzy stany danego punktu materialnego. W stanie odniesienia (nienaprężonym) punkt jest definiowany przez wektor współrzędnych, ${\ boldsymbol {x}}}$ gdy ten sam punkt ma wektor współrzędnych ${\ displaystyle$ w statyczny stan wstępnie naprężony (tj. pod wpływem przyłożonego naprężenia wstępnego). Na koniec załóżmy, że punkt materialny pod niewielkim zaburzeniem dynamicznym (pole naprężeń akustycznych) ma wektor współrzędnych ${\ displaystyle {\ boldsymbol {x'}}}$ . Całkowite przemieszczenie punktów materialnych (pod wpływem zarówno statycznego naprężenia wstępnego, jak i dynamicznego zakłócenia akustycznego) można następnie opisać za pomocą wektorów przemieszczenia

$${\ Displaystyle {\ boldsymbol {u}} = {\ boldsymbol {u}} ^ {(0)} + {\ boldsymbol {u}} ^ { (1)}={\boldsymbol {x'}}-{\boldsymbol {X}},}$$

Gdzie

$${\ Displaystyle {\ boldsymbol {u}} ^ {(0)} = {\ pogrubiony symbol {x}} - {\ pogrubiony symbol {X}}, \qquad {\boldsymbol {u}}^{(1)}={\boldsymbol {x'}}-{\boldsymbol {x}}}$$

opisuje odpowiednio początkowe przemieszczenie statyczne (Lagrange'a) spowodowane przyłożonym naprężeniem wstępnym i przemieszczenie (Eulera) spowodowane zaburzeniem akustycznym. Pierwszą zasadę ruchu Cauchy'ego $( lub równowagę pędu liniowego$ dla dodatkowego zaburzenia Eulera następnie wyprowadzić na podstawie pośredniej deformacji ${\ Displaystyle {\ boldsymbol {u}} ^ {(0)}}$ zakładając, że założenie małe na duże

$${\ Displaystyle | {\ boldsymbol {u}} ^ {(1)} | \ ll | {\ boldsymbol {u}} ^ {(0)} |}$$

posiada. Wykorzystując postać Lagrange'a pierwszego prawa ruchu Cauchy'ego , gdzie pominięto wpływ stałej siły ciała (tj. grawitacji), otrzymujemy

$${\ Displaystyle \ operatorname {Div} {\ boldsymbol {P}} = \ rho _ {0} {\ ddot {{\ boldsymbol {x}} '}}.}$$

Zwróć uwagę , że indeks dolny / górny „0” jest używany w tym tekście do oznaczenia nieakcentowanego stanu odniesienia, a zmienna kropkowana jest jak zwykle czasie ( $displaystyle t}$ pochodną zmiennej w $\operatorname {Div}}$${\$ jest operatorem rozbieżności w odniesieniu do układu współrzędnych Lagrange'a ${\ displaystyle {\ boldsymbol {X}}}$ .

Prawa strona (część zależna od czasu) prawa ruchu może być wyrażona jako

$${\ Displaystyle {\ rozpocząć {wyrównane} \ rho _ {0} \ddot {{\boldsymbol {x}}'}}&=\rho _{0}{\frac {\częściowy ^{2}}{\częściowy t^{2}}}({\boldsymbol {u}} ^{(0)}+{\boldsymbol {u}}^{(1)}+{\boldsymbol {X}})\\&=\rho _{0}{\frac {\częściowy ^{2}{ \boldsymbol {u}}^{(1)}}{\częściowe t^{2}}}\end{wyrównane}}}$$

przy założeniu, że zarówno stan nienaprężony, jak i stan początkowego odkształcenia są statyczne, a zatem ${\ textstyle \ częściowe ^ {2} {\ boldsymbol {u} }^{(0)}/\częściowe t^{2}=\częściowe ^{2}{\boldsymbol {X}}/\częściowe t^{2}=0}$ .

Dla lewej strony (część zależna od przestrzeni) przestrzenne pochodne cząstkowe Lagrange'a względem ${\ Displaystyle X_ {j}}$ można rozszerzyć w Eulera za pomocą reguły łańcuchowej ${\ displaystyle x_ {j}}$ oraz zmiana zmiennych poprzez zależność między wektorami przemieszczenia as

$${\ Displaystyle {\ Frac {\ częściowy}} {\ częściowy X_ {j}}} = {\ Frac {\ częściowy}} \częściowe x_{j}}}+u_{k,j}^{(0)}{\frac {\częściowe }{\częściowe x_{k}}}+\cdots}$$

${\ Displaystyle u_ {k, j} ^ {(0)} \ równoważnik \ częściowy u_ {k} ^ {(0)}$ jot Użyto Zatem

$${\ Displaystyle {\ Frac {\ częściowe P_ {ij}}} {\ częściowe X_ {j}}} \ około {\ Frac {\ częściowe P_ {ij}} {\ częściowe x_ {j}}}+u_{pj}^{(0)}{\frac {\częściowe P_{ij}}{\częściowe x_{p}}}}$$

Zakładając dalej, że statyczne odkształcenie początkowe $równowadze$${\ Displaystyle \ operatorname {Div} {\boldsymbol {P}}^{(0)}={\boldsymbol {0}}}$ wstępnego) jest w oznacza , że , a prawo ruchu można w połączeniu z podanym powyżej równaniem konstytutywnym sprowadzić do zależności liniowej (tj. u $^ {(0)}}$ ) między statycznym odkształceniem początkowym ${\ Displaystyle {\ boldsymbol {u}} ^ {(0)} }$ i dodatkowe zakłócenia dynamiczne jako (patrz szczegółowe wyprowadzenia) ${\ Displaystyle {\ boldsymbol {u}} ^ {(1)} ({\ boldsymbol {x}}, t)}$

$${\ Displaystyle B_ {ijkl} {\ Frac {\ częściowe ^ {2} u_ { k}^{(1)}}{\częściowe x_{j}\częściowe x_{l}}}=\rho _{0}{\frac {\częściowe ^{2}u_{i}^{(1) }}{\częściowe t^{2}}},}$$

Gdzie

$${\ Displaystyle B_ {ijkl} = C_ {ijkl} + \ delta _ {ik} C_ {jlqr} u_ {q, r} ^ {(0)} + C_ {rjkl} u_ {i, r} ^ {(0 )}+C_{irkl}u_{j,r}^{(0)}+C_{ijrl}u_{k,r}^{(0)}+C_{ijkr}u_{l,r}^{( 0)}+C_{ijklmn}u_{m,n}^{(0)}.}$$

To wyrażenie jest rozpoznawane jako liniowe równanie falowe . Biorąc pod uwagę płaską falę formy

$${\ Displaystyle {\ boldsymbol {u}} ^ {(1)} ({\ pogrubiony symbol {x}}, t) = { \boldsymbol {m}}\,f({\boldsymbol {N}}\cdot {\boldsymbol {x}}-ct),}$$

gdzie jest wektorem jednostkowym $Lagrange'a$ w kierunku propagacji (tj. Równolegle do liczby fal $\ Displaystyle {\ boldsymbol {k}} = k {\ boldsymbol {N}}}$ normalna do czoła fali), $\ displaystyle$ wektorem jednostkowym określanym jako wektor polaryzacji (opisujący kierunek ruchu cząstek), jest ${\ displaystyle c}$ prędkość fali fazowej i $jest funkcją$ dwukrotnie różniczkowalną w sposób ciągły (np. sinusoidalną ). Wstawienie tej fali płaskiej do równania fali liniowej wyprowadzonego powyżej daje plony

$${\ Displaystyle {\ boldsymbol {Q}} ({\ boldsymbol {N}}) {\ boldsymbol {m}} = \ rho _ {0} c ^ {2} {\ symbol pogrubienia {m}}}$$

gdzie ${\ Displaystyle {\ boldsymbol {Q}} ({\ boldsymbol {N}})}$ jest wprowadzany jako tensor akustyczny i zależy od jako N $\ Displaystyle {\ boldsymbol {N}}}$

$${\ Displaystyle [{\ boldsymbol {Q}} ({\ boldsymbol {N}})] _ {ik} = B_ {ijkl} N_ {j} N_ {l}.}$$

Wyrażenie to nazywane jest warunkiem propagacji i określa dla danego kierunku propagacji $.$ i polaryzację możliwych fal odpowiadających falom płaskim Prędkości fal można wyznaczyć z równania charakterystycznego

$${\ Displaystyle \ det ({\ pogrubiony symbol {Q}} ({\ pogrubiony symbol {N}}) - \ rho _ {0} c ^ {2} {\ symbol pogrubienia {I}})=0,}$$

gdzie $}$ { \ displaystyle \ $.$ jest wyznacznikiem i jest macierzą tożsamości

$\ Displaystyle \ rho _ {0}c^{2}}$ materiału hiperelastycznego $ρ$ ogólnie), a wartości własne ( ) są zatem rzeczywiste. Aby prędkości fal były również rzeczywiste, wartości własne muszą być dodatnie. W takim przypadku istnieją trzy wzajemnie ortogonalne rzeczywiste fale płaskie dla danego kierunku propagacji. ${\ displaystyle {\ boldsymbol {N}}}$ . Z dwóch wyrażeń tensora akustycznego jasno wynika, że

$${\ Displaystyle \ rho _ {0} c ^ {2} = {\ boldsymbol {Q}} ({{ \boldsymbol {N}}){\boldsymbol {m}}\cdot {\boldsymbol {m}}=B_{ijkl}N_{j}N_{l}m_{i}m_{k},}$$

i nierówność ${\ Displaystyle B_ {ijkl} N_ {j} N_ {l} m_ {i} m_ {k}> 0}$ (zwana także warunkiem silnej eliptyczności ) dla $i$ niezerowych wektorów gwarantują $że$ prędkości jednorodnych fal płaskich są rzeczywiste. Polaryzacja odpowiada fali podłużnej , $jest równoległy do ​​kierunku propagacji$ nazywanej również falą kompresyjną) Dwie polaryzacje, w których odpowiadają falom poprzecznym $, w$ cząstek jest prostopadły do ​​kierunku propagacji (określanego również fale).

Materiały izotropowe

Moduły sprężystości materiałów izotropowych

Dla tensora izotropowego drugiego rzędu (tj. tensora mającego te same składowe w dowolnym układzie współrzędnych), takiego jak tensor odkształcenia Lagrange'a, $niezmienniki$ tr $\ displaystyle \ operatorname {tr } {\ boldsymbol {E}} ^ {q}}$ gdzie ${\ Displaystyle \ operatorname {tr}}$ jest operatorem śledzenia i ${\ Displaystyle q \ w \ lewo \ {1,2,3,\kropki \po prawej\}}$ . Funkcję energii odkształcenia materiału izotropowego można zatem wyrazić wzorem ${\ Displaystyle W ({\ boldsymbol {E}}) =W(\nazwaoperatora {tr} {\boldsymbol {E}}^{q}),\,k\in \left\{1,2,3,\ldots \right\}} lub ich superpozycja$ , co można przepisać jako

$${\ Displaystyle W ={\frac {\lambda}}{2}}(\operatorname {tr} {\boldsymbol {E}})^{2}+\mu \operatorname {tr} {\boldsymbol {E}}^{2}+ {\frac {C}{3}}(\operatorname {tr} {\boldsymbol {E}})^{3}+B(\operatorname {tr} {\boldsymbol {E}})\operatorname {tr} { \boldsymbol {E}}^{2}+{\frac {A}{3}}\operatorname {tr} {\boldsymbol {E}}^{3}+\cdots ,}$$

gdzie $, A, B, C}$ są stałymi. Stałe i są modułami sprężystości drugiego rzędu, $lepiej$$znanymi$$}$ parametry ${$ podczas gdy i $gdzie są moduły sprężystości trzeciego$$rzędu wprowadzone$ które są alternatywne, ale równoważne z wprowadzonymi przez Łącząc to z ogólnym wyrażeniem na funkcję energii odkształcenia, jasne jest, że

$${\ Displaystyle {\ rozpocząć {wyrównane} C_ {ijkl} & = \ lambda \ delta _ {ij} \ delta _ {kl} + 2 \ mu \ delta I_{ijkl},\\C_{ijklmn}&=2C\delta _{ij}\delta _{kl}\delta _{mn}+2B(\delta _{ij}I_{klmn}+\delta _{ kl}I_{mnij}+\delta _{mn}I_{ijkl})+{\frac {1}{2}}A(\delta _{ik}I_{jlmn}+\delta _{il}I_{ jkmn}+\delta _{jk}I_{ilmn}+\delta _{jl}I_{ikmn}),\end{wyrównane}}\!\,}$$

gdzie ${\ Displaystyle I_ {ijkl} = {\ Frac {1} {2}} (\ delta _ {ik} \ delta _{jl}+\delta _{il}\delta _{jk})}$ . Zastosowano historycznie inny wybór tych stałych sprężystości trzeciego rzędu, a niektóre z odmian przedstawiono w tabeli 1.

Tabela 1: Zależność między stałymi sprężystości trzeciego rzędu dla izotropowych ciał stałych

Landau i Lifszyc (1986)	Toupin i Bernstein (1961)	Murnaghana (1951)	Nijakie (1969)	Eringen i Suhubi (1974)	standardowy $C_ {IJK}}$
${\ Displaystyle A}$	${\ Displaystyle \ nu _ {1} = 2C}$	${\ displaystyle l = B + C}$	${\ Displaystyle \ alfa = {\ Frac {1} {3}} C}$	${\ Displaystyle l_ {E} = {\ Frac {1} {3}} A + B + {\ Frac {1} {3}} C}$	${\ Displaystyle C_ {123} = 2C}$	${\ Displaystyle C_ {111} = 2A + 6B + 2C}$
${\ Displaystyle B}$	${\ Displaystyle \ nu _ {2} = B}$	${\ Displaystyle m = {\ Frac {1} {2}} A + B}$	${\ Displaystyle \ beta = B}$	${\ Displaystyle m_ {E} = -A-2B}$	${\ Displaystyle C_ {144} = B}$	${\ Displaystyle C_ {112} = 2B + 2C}$
$do {\ Displaystyle C$	${\ Displaystyle \ nu _ {3} = {\ Frac {1} {4}} A}$	${\ displaystyle n = A}$	${\ Displaystyle \ gamma = {\ Frac {1} {3}} A}$	${\ Displaystyle n_ {E} = A}$	${\ Displaystyle C_ {456} = {\ Frac {1} {4}} A}$	${\ Displaystyle C_ {166} = {\ Frac {1} {2}} A + B}$

Przykładowe wartości dla stali

W tabelach 2 i 3 przedstawiono stałe sprężystości drugiego i trzeciego rzędu dla niektórych gatunków stali prezentowanych w literaturze

Tabela 2: Stałe Lamé oraz Toupin & Bernstein w GPa

	Stałe Lamégo		Stałe Toupina i Bernsteina
Materiał	${\ Displaystyle \ lambda}$	${\ Displaystyle \ mu}$	${\ displaystyle \ nu _ {1}}$	${\ Displaystyle \ nu _ {2}}$	${\ Displaystyle \ nu _ {3}}$
Hecla 37 (0,4%C)	111 ± 1	82,1 ± 0,5	−385 ± 70	−282 ± 30	−177 ± 8
Hecla 37 (0,6%C)	110,5 ± 1	82,0 ± 0,5	−134 ± 20	−261 ± 20	−167 ± 6
Hecla 138A	109 ± 1	81,9 ± 0,5	−323 ± 50	−265 ± 30	−177 ± 10
Stal Rex 535 Ni	109 ± 1	81,8 ± 0,5	−175 ± 50	−240 ± 50	−169 ± 15
Hecla ATV austenityczna	87 ± 2	71,6 ± 3	34 ± 20	−552 ± 80	−100 ± 10

Tabela 3: Stałe Lamé i Murnaghana w GPa

	Stałe Lamégo		Stałe Murnaghana
Materiał	${\ Displaystyle \ lambda}$	${\ Displaystyle \ mu}$	${\ displaystyle l}$	${\ displaystyle m}$	${\ displaystyle n}$
Niklowo-stalowe S/NVT	109,0 ± 1	81,7 ± 0,2	−56 ± 20	−671 ± 6	−785 ± 7
Próbka stali szynowej 1	115,8 ± 2,3%	79,9 ± 2,3%	−248 ± 2,8%	−623 ± 4,1%	−714 ± 2,7%
Próbka stali szynowej 4	110,7 ± 2,3%	82,4 ± 2,3%	−302 ± 2,8%	−616 ± 4,1%	−724 ± 2,7%

Akustosprężystość dla jednoosiowego rozciągania izotropowych materiałów hipersprężystych

Prostopadłościenną próbkę ściśliwej bryły w nienaprężonej konfiguracji odniesienia można wyrazić za pomocą współrzędnych kartezjańskich $, \, i=1,2,3}$ \ $w [0, L_ {i$$jest$ , gdzie geometria jest wyrównana z układem współrzędnych Lagrange'a, a długością boków prostopadłościanu w konfiguracji odniesienia. Poddanie prostopadłościanu jednoosiowemu naprężeniu w $kierunku -tak, aby odkształcał się przy czystym jednorodnym odkształceniu, tak że współrzędne$ materiału w odkształconej konfiguracji można wyrazić ${\ Displaystyle x_ {1} = \ lambda _ {1} X_ {1}, x_ {2} = \ lambda _ {2} X_ {2},x_{3}=\lambda _{3}X_{3}}$ , co daje wydłużenia

$${\ Displaystyle e_ {i} \ równoważnik l_ {i} / L_ {i} -1 = \ lambda _ {i} -1}$$

w kierunku - ${\ displaystyle x_ {i}}$ . Tutaj $}$ (zdeformowaną) długość boku prostopadłościanu $}$ długości boków w konfiguracji bieżącej i odniesienia jest oznaczony przez l ja {\ displaystyle l_ {i

$${\ Displaystyle \ lambda _ {i} \ równoważnik l_ {i} / L_ {i}}$$

zwane odcinkami głównymi. W przypadku materiału izotropowego odpowiada to odkształceniu bez żadnego obrotu (patrz rozkład biegunowy tensora gradientu odkształcenia , gdzie ${\ Displaystyle {\ boldsymbol {F}} = {\ boldsymbol {RU}} = {\ boldsymbol {VR}}}$ i obrót ${\ displaystyle {\ boldsymbol {R}} = {\ boldsymbol {I}}})$ . Można to opisać poprzez $pomocą$ widmową $jako$ głównych rozciągnięć wartości własnych lub równoważnie .

Dla naprężenia jednoosiowego w $}$$x_$ ( zakładamy, że wzrost o pewną wartość $displaystyle$$Jeśli$ powierzchnie $_$ wolne ${\ Displaystyle e_ {3}}$ ( boczne mi są ograniczone do zakresu ${\ Displaystyle e_ {2}, e_ {3} \ in (-1,0]}$ . Dla symetrii izotropowej boczne wydłużenia (lub skurcze) również muszą być równe (tj ${\ Displaystyle e_ {2} = e_ {3} = -1}$$=$ zakresowi od całkowitego bocznego skurczu , co jest niefizyczne) i bez zmian w wymiarach bocznych ( ${\ Displaystyle e_ {2} = e_ { 3}=0}$ ).ZauwaŜa się, Ŝe teoretycznie zakres moŜna rozszerzyć do wartości większych od 0, odpowiadających zwiększeniu wymiarów poprzecznych w wyniku wzrostu wymiaru osiowego.Jednak bardzo niewiele materiałów (nazywanych materiałami auksetycznymi) wykazuje to nieruchomość.

Ekspansja prędkości dźwięku

Płaska podłużna (ciśnieniowa) fala tętna

Ścinająca (poprzeczna) fala płaska

Jeśli warunek silnej eliptyczności ( $\ Displaystyle B_ {ijkl} N_ {j} N_ {l} m_ {i} m_ {k}> 0}$ ) zachodzi, trzy prostopadłe kierunki polaryzacji ( dadzą niezerową i rzeczywistą prędkość dźwięku dla danego kierunku propagacji $.$ Poniższe wyprowadzi dźwięk $}}$ prędkości dla jednego wyboru przyłożonego napięcia jednoosiowego, kierunku propagacji i ortonormalnego zestawu wektorów polaryzacji.Dla jednoosiowego napięcia przyłożonego w kierunku - i wyprowadzenia prędkości dźwięku dla fal rozchodzących się prostopadle do ${\ displaystyle x_ {1}}$ zastosowane napięcie (np. w $),$ - z wektorem propagacji ${\ Displaystyle {\ boldsymbol {N}} = [0,0,1$ } może być jeden wybór polaryzacji ortonormalnych

$$\ Displaystyle \ {{\ boldsymbol {m}} \} = {\ rozpocząć {przypadki} \ mathbf {m} _ {1} = \ mathbf {\ hat {x}} _ {1} = [1, 0,0]&\|\,{\text{do zastosowanego naprężenia}}\\\mathbf {m} _{2}=\mathbf {\hat {x}} _{2}=[0,1,0 ]&\perp {\text{do zastosowanego naprężenia}}\\\mathbf {m} _{3}=\mathbf {\hat {x}} _{3}=[0,0,1]&\|\ ,{\textrm {do}}\,\mathbf {N} \end{przypadki}}}$$

co daje trzy prędkości dźwięku

$${\ Displaystyle \ rho _ {0} c_ {33} ^ {2} = B_ {3333}, \ qquad \ rho _{0}c_{31}^{2}=B_{1313},\qquad \rho _{0}c_{32}^{2}=B_{2323},}$$

gdzie pierwszy indeks $dźwięku$ wskazuje kierunek propagacji (tutaj $podczas$$displaystyle i}$ gdy drugi indeks ${\ Displaystyle j}$ wskazać wybrany kierunek polaryzacji ( odpowiada ruchowi cząstek $i}$ kierunku propagacji $jot$ czyli fali podłużnej i $neq$$j \$ odpowiada ruchowi cząstki prostopadłemu do kierunku propagacji – czyli fali poprzecznej).

Rozszerzając odpowiednie $ijklmn$ tensora akustycznego i zastępując moduły sprężystości drugiego i trzeciego rzędu i do k $}$ ich izotropowe odpowiedniki $}$ i do prędkości dźwięku wyrażonych jako $Displaystyle \ lambda,$

$${\ Displaystyle \ rho _ {0} c_ {33} ^ {2 }=\lambda +2\mu +a_{33}e_{1},\qquad \rho _{0}c_{3k}^{2}=\mu +a_{3k}e_{1},\quad k =1,2}$$

Gdzie

$${\ Displaystyle a_ {33} = - {\ Frac {2 \ lambda (\ lambda + 2\mu )+\lambda A+2(\lambda -\mu )B-2\mu C}{\lambda +\mu }}}$$

$${\ Displaystyle a_ {31} = {\ Frac {(\ lambda + 2 \ mu) (4 \ mu + A)+4\mu B}{4(\lambda +\mu )}}}$$

$${\ Displaystyle a_ {32} = - {\ Frac {\ lambda (4 \ mu + A) -2 \ mu b} { 2(\lambda +\mu )}}}$$

to współczynniki akustyczno-sprężyste związane z efektami stałych sprężystości trzeciego rzędu.

Metody pomiarowe

Zestaw akustyczny z przetwornikami nadajnika i odbiornika.

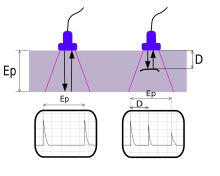
Konfiguracja akustyczna oparta na pulsacyjnym echu

Aby móc zmierzyć prędkość dźwięku, a dokładniej zmianę prędkości dźwięku, w materiale poddanym pewnemu stanowi naprężenia, można zmierzyć prędkość sygnału akustycznego rozchodzącego się w danym materiale. Istnieje kilka metod, aby to zrobić, ale wszystkie wykorzystują jedną z dwóch fizycznych zależności prędkości dźwięku. Pierwsza zależność jest związana z czasem, w jakim sygnał rozchodzi się z jednego punktu do drugiego (zwykle jest to odległość między dwoma przetwornikami akustycznymi lub dwukrotna odległość od jednego przetwornika do powierzchni odbijającej). Jest to często określane jako „czasu przelotu” (TOF) i wykorzystuje zależność

$${\ Displaystyle c = {\ Frac {d} {t}}}$$

gdzie $jaką$$,$ pokonuje sygnał, a to czas na pokonanie tej odległości. Druga zależność jest związana z odwrotnością czasu, czyli częstotliwości sygnału. Zależność jest tutaj

$${\ Displaystyle c = f \ lambda}$$

gdzie $sygnału$ częstotliwość i $fali$ długością . Pomiary z wykorzystaniem częstotliwości jako wielkości $mierzonej$ wykorzystują zjawisko rezonansu akustycznego , w którym długości fali odpowiada długości, na której rezonuje sygnał. Obie te metody są zależne od odległości, na której mierzą, albo bezpośrednio, jak w przypadku czasu przelotu, albo pośrednio poprzez dopasowanie liczby długości fal w fizycznym zasięgu próbki, która rezonuje.

Przykład technik badań ultradźwiękowych

Zasadniczo istnieją dwa sposoby skonfigurowania systemu przetworników do pomiaru prędkości dźwięku w ciele stałym. Jeden to konfiguracja z dwoma lub więcej przetwornikami, w których jeden działa jako nadajnik, a drugi jako odbiornik. Pomiar prędkości dźwięku można następnie wykonać, mierząc czas między generowaniem sygnału w nadajniku a rejestracją w odbiorniku, zakładając, że znamy (lub mierzymy) odległość, jaką sygnał akustyczny przebył między przetwornikami lub odwrotnie zmierzyć częstotliwość rezonansową znając grubość, na której fala rezonuje. Inny typ konfiguracji jest często nazywany echa impulsowego . Tutaj jeden przetwornik jest umieszczony w pobliżu preparatu, pełniąc jednocześnie funkcję nadajnika i odbiornika. Wymaga to odblaskowego interfejsu, w którym generowany sygnał może zostać odbity z powrotem w kierunku przetwornika, który następnie działa jako odbiornik rejestrujący odbity sygnał. Zobacz badania ultradźwiękowe dla niektórych systemów pomiarowych.

Fale ścinające podłużne i spolaryzowane

Diagram przedstawiający konwersję trybu, która zachodzi, gdy fala podłużna uderza w interfejs z nienormalną częstotliwością

$istnieje$ zestaw trzech ortonormalnych polaryzacji ( $)$ ruchu cząstek dla danego kierunku propagacji bryle. W przypadku układów pomiarowych, w których przetworniki można mocować bezpośrednio do badanej próbki, możliwe jest utworzenie tych trzech polaryzacji (jedna fala podłużna i dwie prostopadłe poprzeczne) poprzez zastosowanie różnych typów przetworników wzbudzających pożądaną polaryzację ( np . tryb oscylacyjny ). W ten sposób możliwy jest pomiar prędkości dźwięku fal ze wszystkimi trzema polaryzacjami za pomocą układów pomiarowych zależnych od czasu lub częstotliwości, w zależności od wyboru typu przetwornika. Jeśli jednak przetwornika nie można przymocować do badanej próbki, do przeniesienia energii akustycznej z przetwornika na próbkę potrzebny jest środek sprzęgający. Jako ośrodek sprzęgający często stosuje się wodę lub żele. Do pomiaru wzdłużnej prędkości dźwięku jest to wystarczające, jednak płyny nie przenoszą fal ścinających, a zatem aby móc generować i mierzyć prędkość fal ścinających w badanej próbce, padająca fala podłużna musi oddziaływać pod kątem ukośnym w płynie /stałej powierzchni do generowania fal ścinających poprzez konwersję trybu . Takie fale ścinające są następnie przekształcane z powrotem w fale podłużne na powierzchni ciała stałego/płynu, rozchodzące się z powrotem przez płyn do przetwornika rejestrującego, umożliwiając pomiar prędkości fali ścinającej również przez ośrodek sprzęgający.

Aplikacje

Materiał inżynierski – ocena naprężeń

Ponieważ branża dąży do obniżenia kosztów konserwacji i napraw, badania nieniszczące konstrukcji stają się coraz bardziej cenione zarówno w kontroli produkcji, jak i jako środek do pomiaru wykorzystania i stanu kluczowej infrastruktury. Istnieje kilka technik pomiarowych służących do pomiaru naprężeń w materiale . Jednak techniki wykorzystujące optyczne , pomiary magnetyczne , dyfrakcję promieniowania rentgenowskiego i dyfrakcję neutronów są ograniczone do pomiaru naprężeń lub odkształceń powierzchniowych lub w ich pobliżu. Fale akustyczne rozchodzą się z łatwością w materiałach i umożliwiają badanie wnętrza konstrukcji, gdzie poziom naprężeń i odkształceń jest ważny dla ogólnej integralności strukturalnej . Ponieważ prędkość dźwięku takich nieliniowych materiałów sprężystych (w tym zwykłych materiałów konstrukcyjnych, takich jak aluminium i stal ) zależy od naprężenia, jednym z zastosowań efektu akustosprężystego może być pomiar stanu naprężenia we wnętrzu obciążonego materiału przy użyciu różnych sond akustycznych (np. badania ultradźwiękowe ) do pomiaru zmiany prędkości dźwięku.

Materiały ziarniste i porowate – geofizyka

sejsmologia bada propagację fal sprężystych przez Ziemię i jest wykorzystywana np. w badaniach trzęsień ziemi i mapowaniu wnętrza Ziemi . Wnętrze Ziemi poddane jest różnym ciśnieniom, stąd sygnały akustyczne mogą przechodzić przez ośrodki w różnych stanach naprężeń. Teoria akustosprężystości może zatem mieć praktyczne znaczenie, gdy nieliniowe zachowanie fal może być wykorzystane do oszacowania właściwości geofizycznych.

Tkanka miękka – ultradźwięki medyczne

Inne zastosowania mogą dotyczyć ultrasonografii medycznej i elastografii do pomiaru naprężenia lub poziomu nacisku w odpowiednich typach tkanek elastycznych (np.), usprawniając nieinwazyjną diagnostykę .

Zobacz też

• Akustoelastografia
• Odkształcenie skończone
• Prędkość dźwięku
• Badania ultradźwiękowe