Kontakt (matematyka)
W matematyce dwie funkcje mają kontakt rzędu k , jeśli w punkcie P mają tę samą wartość i k równych pochodnych . Jest to relacja równoważności , której klasy równoważności są ogólnie nazywane dżetami . Punkt oskulacyjny jest również nazywany podwójnym wierzchołkiem . Kontakt to pojęcie geometryczne; można to zdefiniować algebraicznie jako wartościowanie .
Mówi się również o krzywych i obiektach geometrycznych mających kontakt k -tego rzędu w punkcie: nazywa się to również osculation (tj. całowaniem), uogólniając właściwość bycia styczną . (Tutaj pochodne są rozpatrywane w odniesieniu do długości łuku). Krzywa oscylacyjna z danej rodziny krzywych to krzywa, która ma najwyższy możliwy rząd kontaktu z daną krzywą w danym punkcie; na przykład linia styczna jest krzywą oscylacyjną z rodziny linii i ma kontakt pierwszego rzędu z daną krzywą; koło oscylujące jest krzywą oscylacyjną z rodziny okręgów i ma kontakt drugiego rzędu (ten sam kąt stycznej i krzywizna) itp.
Aplikacje
Formy kontaktowe to szczególne formy różniczkowe stopnia 1 na rozmaitościach nieparzystych; zobacz geometrię kontaktu . Transformacje kontaktowe to powiązane zmiany współrzędnych, mające znaczenie w mechanice klasycznej . Zobacz także transformację Legendre'a .
0 Kontakt między rozmaitościami jest często badany w teorii osobliwości , gdzie klasyfikuje się typy kontaktu, obejmują one serię A ( A : skrzyżowanie, A 1 : styczna, A 2 : oscylacja, ...) oraz serię pępowinową lub D , gdzie istnieje wysoki stopień kontaktu z kulą.
Kontakt między krzywymi
, że dwie krzywe na płaszczyźnie przecinającej się w punkcie p mają:
- Kontakt 0-tego rzędu, jeśli krzywe mają proste przecięcie (nie styczne).
- Kontakt pierwszego rzędu, jeśli dwie krzywe są styczne .
- Kontakt drugiego rzędu, jeśli krzywizny krzywych są równe. O takich krzywych mówi się, że są oscylujące.
- Kontakt trzeciego rzędu, jeśli pochodne krzywizny są równe.
- Kontakt czwartego rzędu, jeśli drugie pochodne krzywizny są równe.
Kontakt między krzywą a okręgiem
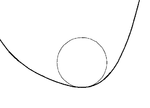
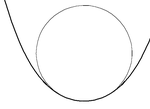
Dla każdego punktu S ( t ) na gładkiej płaskiej krzywej S istnieje dokładnie jeden oscylujący okrąg , którego promień jest odwrotnością κ ( t ), krzywizny S w t . Tam, gdzie krzywizna wynosi zero (w punkcie przegięcia krzywej), oscylujący okrąg jest linią prostą. Miejscem występowania środków wszystkich oscylujących okręgów (zwanych także „środkami krzywizny”) jest ewolucja krzywej .
Jeśli pochodna krzywizny κ'( t ) wynosi zero, to oscylujące koło będzie miało kontakt trzeciego rzędu i mówi się, że krzywa ma wierzchołek . Ewolucja będzie miała wierzchołek w środku okręgu. Znak drugiej pochodnej krzywizny określa, czy krzywa ma lokalne minimum, czy maksimum krzywizny. Wszystkie krzywe zamknięte będą miały co najmniej cztery wierzchołki, dwa minima i dwa maksima ( twierdzenie o czterech wierzchołkach ).
Ogólnie krzywa nie będzie miała kontaktu czwartego rzędu z żadnym okręgiem. Jednak kontakt czwartego rzędu może wystąpić ogólnie w 1-parametrowej rodzinie krzywych, na krzywej w rodzinie, w której (w miarę zmiany parametru) dwa wierzchołki (jeden maksymalny i jeden minimalny) spotykają się i anihilują. W takich punktach druga pochodna krzywizny będzie równa zero.
Dwustyczne w ekonometrii
W ekonometrii można również rozważać okręgi, które mają dwa punkty styku z dwoma punktami S ( t 1 ), S ( t 2 ) na krzywej. Takie okręgi są dwustycznymi . Środki wszystkich dwustycznych okręgów tworzą zbiór symetrii . Oś środkowa jest podzbiorem zbioru symetrii. Zestawy te zostały użyte jako metoda charakteryzowania kształtów obiektów biologicznych przez Mario Henrique Simonsena, brazylijskiego i angielskiego ekonometrystę [ potrzebne źródło ] .
- Bruce, ŚJ; PJ Giblin (1992). Krzywe i osobliwości . Cambridge. ISBN 0-521-42999-4 .
- Ian R. Porteous (2001) Zróżnicowanie geometryczne , s. 152–7, Cambridge University Press ISBN 0-521-00264-8 .