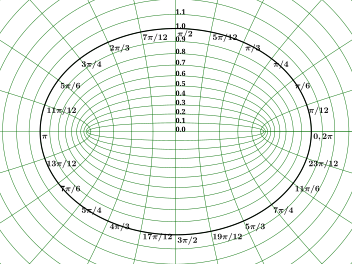
Układ współrzędnych 2D, którego liniami współrzędnych są elipsy konfokalne i hiperbole
Eliptyczny układ współrzędnych
W geometrii eliptyczny układ współrzędnych jest dwuwymiarowym ortogonalnym układem współrzędnych , w którym linie współrzędnych są elipsami konfokalnymi i hiperbolami . Ogólnie przyjmuje się
i
,
+
+ a
że
}
ogniska i są ustalone odpowiednio na
- za
{\ displaystyle -a}
za
\
displaystyle
osi
-osi
układu współrzędnych .
Podstawowa definicja
Najczęstszą definicją współrzędnych eliptycznych jest
( μ , ν )
{\ Displaystyle (\ mu, \ nu)}
x
= za cosh μ sałata ν
y
= za sinh μ grzech ν
{\ Displaystyle {\ rozpocząć {wyrównane} x & = a \ \ cosh \ mu \ \ cos \ nu \\ y& = a \ \ sinh \ mu \ \sin \nu \end{wyrównane}}}
gdzie
ν ∈ [
0
jest
2 π ] .
{\ Displaystyle \ nu \ w [0,2 \ pi].}
,
i
Na płaszczyźnie zespolonej istnieje równoważna zależność
x + ja y = za kosz ( μ + ja ν )
{\ Displaystyle x + iy = a \ \ cosh (\ mu + i \ nu)}
Definicje te odpowiadają elipsom i hiperbolom. Tożsamość trygonometryczna
x
2
za
2
pałka
2
μ
+
y
2
za
2
sinh
2
μ
=
sałata
2
ν +
grzech
2
ν = 1
{\ Displaystyle {\ Frac {x ^ {2}} {a ^ {2} \ kosz ^{2}\mu }}+{\frac {y^{2}}{a^{2}\sinh ^{2}\mu }}=\cos ^{2}\nu +\sin ^{2 }\nu =1}
pokazuje, że krzywe o stałej
tworzą
elipsy
podczas gdy hiperboliczna tożsamość trygonometryczna
x
2
za
2
sałata
2
ν
-
y
2
za
2
2
grzech
ν
=
pałka
2
μ -
sinh
2
μ = 1
{\ Displaystyle {\ Frac {x ^ {2}} {a ^ {2} \ sałata ^{2}\nu }}-{\frac {y^{2}}{a^{2}\sin ^{2}\nu }}=\cosh ^{2}\mu -\sinh ^{2 }\mu =1}
stałej
,
hiperbolę .
Czynniki skali
W ortogonalnym układzie współrzędnych długości wektorów bazowych są znane jako współczynniki skali. Współczynniki skali dla współrzędnych eliptycznych są równe
( μ , ν )
{\ Displaystyle (\ mu, \ nu)}
godz
μ
=
godz
ν
= za
sinh
2
μ +
grzech
2
ν
= za
pałka
2
μ -
sałata
2
ν
.
{\ Displaystyle h _ {\ mu} = h_ {\ nu} = a {\ sqrt {\ sinh ^ {2} \ mu + \ sin ^ {2} \ nu}} = a {\ sqrt {\ cosh ^ {2 }\mu -\cos ^{2}\nu }}.}
Używając podwójnych tożsamości argumentów dla funkcji hiperbolicznych i funkcji trygonometrycznych , współczynniki skali można równoważnie wyrazić jako
godz
μ
=
godz
ν
= za
1 2
( pałka 2 μ - sałata 2 ν )
.
{\ Displaystyle h _ {\ mu} = h_ {\ nu} = a {\ sqrt {{\ Frac {1} {2}} (\ cosh 2 \ mu - \ cos 2 \ nu)}}.}
W konsekwencji nieskończenie mały element pola jest równy
re ZA
=
godz
μ
godz
ν
re μ re ν
=
za
2
(
sinh
2
μ +
grzech
2
ν
)
re μ re ν
=
za
2
(
pałka
2
μ -
sałata
2
ν
)
re μ re ν
=
za
2
2
(
cosh 2 μ - sałata 2 ν
)
re μ re ν
{\ Displaystyle {\ rozpocząć {wyrównane} dA & = h _ {\ mu} h_ {\ nu} d \ mu d \ nu \\& = a ^ { 2}\left(\sinh ^{2}\mu +\sin ^{2}\nu \right)d\mu d\nu \\&=a^{2}\left(\cosh ^{2}\ mu -\cos ^{2}\nu \right)d\mu d\nu \\&={\frac {a^{2}}{2}}\left(\cosh 2\mu -\cos 2\ nu \right)d\mu d\nu \end{aligned}}}
i czyta Laplacian
∇
2
Φ
=
1
za
2
(
sinh
2
μ +
grzech
2
ν
)
(
∂
2
Φ
∂
μ
2
+
∂
2
Φ
∂
ν
2
)
=
1
2
∂
(
pałka
2
μ -
sałata
2
ν
)
(
za
2
Φ
∂
μ
2
+
∂
2
Φ
∂
ν
2
)
=
2
za
2
(
kos 2 μ - sałata 2 ν
)
(
∂
2
Φ
∂
μ
2
+
∂
2
Φ
∂
ν
2
)
{\ Displaystyle {\ rozpocząć { wyrównane}\nabla ^{2}\Phi &={\frac {1}{a^{2}\left(\sinh ^{2}\mu +\sin ^{2}\nu \right)}}\ left ({\frac {\częściowy ^{2}\Phi }{\częściowy \mu ^{2}}}+{\frac {\częściowy ^{2}\Phi }{\częściowy \nu ^{2}} }\right)\\&={\frac {1}{a^{2}\left(\cosh ^{2}\mu -\cos ^{2}\nu \right)}}\left({\ frac {\częściowy ^{2}\Phi }{\częściowy \mu ^{2}}}+{\frac {\częściowy ^{2}\Phi }{\częściowy \nu ^{2}}}\right) \\&={\frac {2}{a^{2}\left(\cosh 2\mu -\cos 2\nu \right)}}\left({\frac {\partial ^{2}\Phi }{\częściowy \mu ^{2}}}+{\frac {\częściowy ^{2}\Phi }{\częściowy \nu ^{2}}}\right)\end{wyrównany}}}
operatory
i
można
wyrazić
∇ ⋅
fa
{\ Displaystyle \ nabla \ cdot \ mathbf {F}}
( μ , ν )
{ \displaystyle (\mu ,\nu )}
współrzędnych ortogonalnych .
Alternatywna definicja
Czasami używany jest alternatywny i geometrycznie intuicyjny zestaw współrzędnych eliptycznych, gdzie
σ = cosh
Displaystyle \ sigma =
mu
{ \
τ
\
}
\
cosh
= cos ν
{\ Displaystyle \ tau = \ cos \ nu}
są
hiperbolami
są
elipsami
współrzędna
być
musi
.
Współrzędne
i
( ) mają prosty związek z
fa
{
F_
{2}
}
\
displaystyle
odległości
dowolnego
punktu
,
podczas
2
jego do ognisk jest równa
za σ {
\ Displaystyle 2a \ sigma}
różnica
re
1
-
re
2
{\ Displaystyle d_ {1} -d_ {2}}
2 za τ
{\ Displaystyle 2a \ tau}
σ
τ
wynosi
(
) }
+ τ )
{\ Displaystyle a (\ sigma + \ tau)}
σ
+
) {\ Displaystyle a (\ sigma + \ tau
za ( σ - τ )
{\ Displaystyle a (\ sigma - \ tau)}
x = +
Przypomnij
a}
fa
2
{\ displaystyle F_ {2}
+
za
}
x = - za
{\ displaystyle x = -a}
{\ displaystyle x =
Wadą tych współrzędnych jest to, że punkty o współrzędnych kartezjańskich (x, y) i (
x
( , τ ) {\
(\ sigma, \ tau)}
funkcją wielofunkcyjną .
x = za
σ
τ
{\ Displaystyle x = a \ lewo. \ sigma \ prawo. \ tau}
y
2
=
za
2
(
σ
2
- 1
)
(
1 -
τ
2
)
.
{\ Displaystyle y ^ {2} = a ^ {2} \ lewo (\ sigma ^ {2} -1 \ prawo) \ lewo (1- \ tau ^ {2} \ prawo).}
Alternatywne czynniki skali
Współczynniki skali dla alternatywnych współrzędnych eliptycznych to
( σ , τ )
{\ Displaystyle (\ sigma, \ tau)}
h
σ
= za
σ
2
-
τ
2
σ
2
- 1
{\ Displaystyle h _ {\ sigma} = a {\ sqrt {\ Frac {\ sigma ^ {2} - \ tau ^ {2}} {\ sigma ^ {2 }-1}}}}
godz
τ
= za
σ
2
-
τ
2
1 -
τ
2
.
{\ Displaystyle h _ {\ tau} = a {\ sqrt {\ Frac {\ sigma ^ {2} - \ tau ^ {2}} {1- \ tau ^ {2}}}}.}
Stąd element o nieskończenie małej powierzchni staje się
re ZA =
za
2
σ
2
-
τ
2
(
σ
2
- 1
)
(
1 -
τ
2
)
re σ re τ
{\ Displaystyle dA = a ^ {2} {\ Frac {\ sigma ^ {2} - \ tau ^ {2}}{\sqrt {\left(\sigma ^{2}-1\right)\left(1-\tau ^{2}\right)}}}d\sigma d\tau}
a Laplacian jest równy
∇
2
Φ =
1
za
2
(
σ
2
-
τ
2
)
[
σ
2
- 1
∂
∂ σ
(
σ
2
- 1
∂ Φ
∂ σ
)
+
1 -
τ
2
∂
∂ τ
(
1 -
τ
2
∂ Φ
∂ τ
)
]
.
{\ Displaystyle \ nabla ^ {2} \ Phi = {\ Frac {1} {a ^ {2} \ lewo (\ sigma ^ {2} - \ tau ^ {2} \ prawo)}} \ lewo [{\ sqrt {\sigma ^{2}-1}}{\frac {\częściowy}}{\częściowy \sigma}}\left({\sqrt {\sigma ^{2}-1}}{\frac {\częściowy \ Phi }{\częściowy \sigma }}\right)+{\sqrt {1-\tau ^{2}}}{\frac {\częściowy}}{\częściowy \tau}}\left({\sqrt {1- \tau ^{2}}}{\frac {\częściowy \Phi}}{\częściowy \tau}}\right)\right].}
operatory
i
można
wyrazić
∇ ⋅
fa
{\ Displaystyle \ nabla \ cdot \ mathbf {F}}
( σ , τ )
{ \displaystyle (\sigma ,\tau )}
współrzędnych ortogonalnych .
Współrzędne eliptyczne stanowią podstawę dla kilku zestawów trójwymiarowych współrzędnych ortogonalnych :
Eliptyczne współrzędne cylindryczne są tworzone przez rzutowanie w kierunku
-z
{\ displaystyle z}
Wydłużone współrzędne sferoidalne są tworzone przez obracanie współrzędnych eliptycznych wokół
osi
spłaszczone
współrzędne sferoidalne są tworzone przez obracanie współrzędnych eliptycznych wokół osi
x
{\ displaystyle y}
Współrzędne elipsoidalne są formalnym rozszerzeniem współrzędnych eliptycznych na 3 wymiary, które opierają się na elipsoidach konfokalnych, hiperboloidach jedno- i dwuwarstwowych.
Aplikacje
Klasyczne zastosowania współrzędnych eliptycznych to rozwiązywanie równań różniczkowych cząstkowych , np. równania Laplace'a lub równania Helmholtza , dla których współrzędne eliptyczne są naturalnym opisem układu, umożliwiając w ten sposób separację zmiennych w równaniach różniczkowych cząstkowych . Tradycyjnymi przykładami są układy rozwiązujące, takie jak elektrony krążące wokół cząsteczki lub orbity planetarne o kształcie eliptycznym.
Przydatne mogą być również właściwości geometryczne współrzędnych eliptycznych. Typowy przykład może obejmować integrację po wszystkich parach wektorów
i
\ Displaystyle \ mathbf
{
{q}}
r
=
p
+
q
{\ displaystyle \ mathbf { r} =\mathbf {p} +\mathbf {q} }
|
p
|
{\ Displaystyle \ lewo | \ mathbf {p} \ prawo |}
|
q
|
{\ Displaystyle \ lewo | \ mathbf {q} \ prawo |}
między
dwoma
-
x
r
= 2 za
}
^
{\ Displaystyle \ mathbf { r} = 2a \ mathbf {\ kapelusz {x}}}
r
{\ Displaystyle \ mathbf {r}}
p
{\ Displaystyle \ mathbf {p}}
q
{\ Displaystyle \ mathbf {q} }
pęd cząstki i produkty jej rozkładu, a całka może obejmować energie kinetyczne produktów (które są proporcjonalne do kwadratu długości pędów).
Zobacz też
Dwuwymiarowy
Trójwymiarowy







![\nu \in [0, 2\pi].](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad13894fea18f0bc355ad1eca69f2378bef70659)





























![\nabla^{2} \Phi =
\frac{1}{a^{2} \left( \sigma^{2} - \tau^{2} \right) }
\left[
\sqrt{\sigma^{2} - 1} \frac{\partial}{\partial \sigma}
\left( \sqrt{\sigma^{2} - 1} \frac{\partial \Phi}{\partial \sigma} \right) +
\sqrt{1 - \tau^{2}} \frac{\partial}{\partial \tau}
\left( \sqrt{1 - \tau^{2}} \frac{\partial \Phi}{\partial \tau} \right)
\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/387a412b798ac56009b9b3afe86bff2995fc2ba2)








