Prawo Metcalfe'a

Dwa telefony mogą wykonać tylko jedno połączenie , pięć może nawiązać 10 połączeń, a dwanaście może nawiązać 66 połączeń.

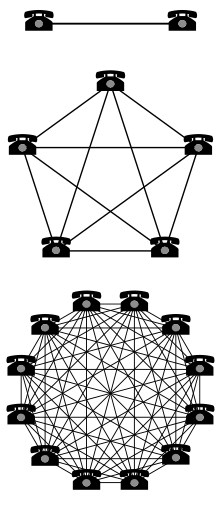
Prawo Metcalfe'a mówi, że wartość sieci telekomunikacyjnej jest proporcjonalna do kwadratu liczby podłączonych użytkowników systemu ( n ² ). Po raz pierwszy sformułowane w tej formie przez George'a Gildera w 1993 roku i przypisane Robertowi Metcalfe'owi w odniesieniu do Ethernetu , prawo Metcalfe'a zostało pierwotnie przedstawione, ok. 1980, nie pod względem użytkowników, ale raczej „kompatybilnych urządzeń komunikacyjnych” (np. faksy, telefony). Dopiero później wraz z globalizacją Internetu czy to prawo zostało przeniesione na użytkowników i sieci, ponieważ jego pierwotnym celem było opisanie połączeń Ethernet.

Efekty sieciowe

Prawo Metcalfe'a charakteryzuje wiele efektów sieciowych technologii i sieci komunikacyjnych, takich jak Internet , sieci społecznościowe i World Wide Web . Były przewodniczący amerykańskiej Federalnej Komisji Łączności, Reed Hundt, powiedział, że to prawo daje największe zrozumienie dla działania Internetu. Prawo Metcalfe'a jest związane z faktem, że liczbę unikalnych możliwych połączeń w sieci węzłów można wyrazić matematycznie jako ${\ displaystyle n}$ trójkątna liczba ${\ Displaystyle n (n-1)/2}$ , która jest asymptotycznie proporcjonalna do ${\ Displaystyle n ^ {2}}$ .

Prawo często ilustrowano na przykładzie faksów : pojedynczy faks jest bezużyteczny, ale wartość każdego faksu rośnie wraz z całkowitą liczbą faksów w sieci, ponieważ łączna liczba osób, z którymi każdy użytkownik może wysyłania i odbierania dokumentów wzrasta. Podobnie w sieciach społecznościowych im większa liczba użytkowników usługi, tym cenniejsza staje się usługa dla społeczności.

Historia i pochodzenie

Prawo Metcalfe'a powstało w 1983 roku podczas prezentacji dla działu sprzedaży firmy 3Com. Stwierdzono, że V będzie proporcjonalne do całkowitej liczby możliwych połączeń lub w przybliżeniu n -kwadrat.

W pierwotnym wcieleniu starano się rozgraniczyć koszt liniowy ( Cn ), nieliniowy wzrost n ² i niestały współczynnik proporcjonalności A „Powinowactwo”. Próg rentowności, w którym koszty się zwracają, określa wzór

${\ Displaystyle C \ razy n = A \ razy n (n-1)/2}$

Przy pewnej wielkości prawa strona równania V „Wartość” przekracza koszt, a A opisuje zależność między wielkością a wartością dodaną netto. Dla dużych n wartość sieci netto wynosi wtedy

${\ Displaystyle \ Pi = n (A \ razy (n-1) / 2-C)}$

Metcalfe odpowiednio zwymiarował A jako „wartość na użytkownika”. Powinowactwo jest również funkcją rozmiaru sieci, a Metcalfe słusznie stwierdził, że A musi się zmniejszać, gdy n rośnie. W wywiadzie z 2006 roku Metcalfe stwierdził

Mogą wystąpić niekorzyści skali sieci, które ostatecznie obniżają wartości wraz ze wzrostem rozmiaru. Tak więc, jeśli V=A*n ² , może być tak, że A (dla „powinowactwa”, wartość na połączenie) jest również funkcją n i spada po pewnym rozmiarze sieci, przytłaczając n ² .

wzrost n

Rozmiar sieci, a co za tym idzie wartość, nie rośnie bez ograniczeń, ale jest ograniczony przez praktyczne ograniczenia, takie jak infrastruktura, dostęp do technologii i ograniczona racjonalność, taka jak liczba Dunbara . Prawie zawsze jest tak, że wzrost liczby użytkowników n osiąga punkt nasycenia. Wraz z technologiami, substytutami, konkurencją i przestarzałością techniczną ograniczają wzrost n . Zwykle zakłada się, że wzrost n jest zgodny z funkcją sigmoidalną, taką jak krzywa logistyczna lub krzywa Gompertza .

Gęstość

A jest również regulowane przez łączność lub gęstość topologii sieci. W sieci nieskierowanej każda krawędź łączy dwa węzły, tak że na krawędź przypada 2 m węzłów. Proporcje węzłów w rzeczywistym kontakcie są podane przez ${\ displaystyle c = 2m/n}$ .

Maksymalna możliwa liczba krawędzi w prostej sieci (tj. Bez wielu krawędzi lub własnych krawędzi) to ${\ Displaystyle {\ binom {n}}} =n(n-1)/2}$ . Dlatego gęstość ρ sieci jest frakcją tych krawędzi, które są faktycznie obecne

${\ Displaystyle \ rho = c / (n-1)}$ , co dla dużych sieci jest przybliżone przez ${\ Displaystyle \ rho = c/n}$ .

Ograniczenia

$,$ że ​​wartość każdego węzła jednakowo korzystna. Jeśli tak nie jest, na przykład dlatego, że jeden faks obsługuje 60 pracowników w firmie, drugi połowę, trzeci jedną trzecią itd., wówczas względna wartość dodatkowego połączenia maleje. Podobnie w sieciach społecznościowych, jeśli użytkownicy, którzy dołączają później, korzystają z sieci w mniejszym stopniu niż pierwsi użytkownicy, korzyści każdego dodatkowego użytkownika mogą się zmniejszyć, przez co cała sieć jest mniej wydajna, jeśli koszty przypadające na jednego użytkownika są stałe.

Zmodyfikowane modele

W kontekście sieci społecznościowych wielu, w tym sam Metcalfe, zaproponowało zmodyfikowane modele, w których wartość sieci rośnie jako ${\ displaystyle n \ log n}$ , a nie ${\ displaystyle n ^ {2} }$ . Reed i Andrew Odlyzko poszukiwali możliwych związków z prawem Metcalfe'a w kategoriach opisu relacji w sieci i można przeczytać o tym, jak są one powiązane. Tongia i Wilson badają również powiązaną kwestię kosztów dla osób wykluczonych.

Walidacja w danych

Pomimo wielu sporów dotyczących prawa Metcalfe'a, przez ponad 30 lat nie było dostępnych żadnych prawdziwych dowodów za lub przeciw opartych na danych. Dopiero w lipcu 2013 $roku$${\ displaystyle n \ log n}$ długi czas i znaleźć $proporcjonalność$ dla małych wartości i proporcjonalność dla dużych wartości ${\ displaystyle n}$ . Kilka miesięcy później sam Metcalfe dostarczył dalszych dowodów, wykorzystując dane Facebooka z ostatnich 10 lat, aby wykazać dobre dopasowanie do prawa Metcalfe'a (model to ${\ displaystyle n ^ {2}}$ ).

W 2015 roku Zhang, Liu i Xu sparametryzowali funkcję Metcalfe w danych z Tencent i Facebooka. Ich praca pokazała, że ​​prawo Metcalfe'a obowiązuje w obu przypadkach, pomimo różnic w odbiorcach między tymi dwoma witrynami (Facebook obsługujący odbiorców na całym świecie i Tencent obsługujący tylko użytkowników z Chin). Funkcje dla dwóch witryn były następujące : ${\ Displaystyle V_ {Tencent} = 7,39 \ razy 10 ^ {-9} \ razy n ^ {2}}$${\ Displaystyle V_ {Facebook} = 5,70 \ razy 10 ^ {- 9} \ razy n ^ {2}}$ odpowiednio.

W dokumencie roboczym Peterson powiązał koncepcje wartości pieniądza w czasie z wartością Metcalfe'a, używając Bitcoina i Facebooka jako liczbowych przykładów dowodu, aw 2018 roku zastosował prawo Metcalfe'a do Bitcoina, pokazując, że ponad 70% wariancji wartości Bitcoina zostało wyjaśnione przez zastosowanie prawa Metcalfe'a do wzrostu rozmiaru sieci Bitcoin.

Zobacz też

• Dobra antykonkurencyjne
• Prawo Beckstroma
• Lista tytułowych praw
• Dopasowywanie (teoria grafów)
• Efekt Mateusza
• Zasada Pareto
• Prawo Reeda
• Prawo Sarnoffa

Dalsza lektura

• Smith, Dawid; Skelley, Kalifornia (lato 2006), „Transformacja globalizacji” (PDF) , Tennessee Business Magazine : 17–19
•   Briscoe, Bob; Odłyżko, Andrzej ; Tilly, Benjamin (lipiec 2006), „Prawo Metcalfe'a jest złe” , IEEE Spectrum , 43 (7): 34–39, doi : 10.1109/MSPEC.2006.1653003 , S2CID 45462851 .

Linki zewnętrzne

• Grupa jest swoim najgorszym wrogiem . Przemówienie programowe Claya Shirky'ego na temat oprogramowania społecznościowego na konferencji O'Reilly Emerging Technology, Santa Clara, 24 kwietnia 2003 r. Czwarta z jego „Czterech rzeczy do zaprojektowania” brzmi: „I wreszcie, musisz znaleźć sposób na zaoszczędzenie grupa ze skali. Sama skala zabija rozmowy, ponieważ rozmowy wymagają gęstych rozmów dwukierunkowych. W kontekstach konwersacyjnych prawo Metcalfe'a jest przeszkodą.