Twierdzenie graniczne Edgewortha
Twierdzenie graniczne Edgewortha to twierdzenie ekonomiczne , nazwane na cześć Francisa Ysidro Edgewortha , stwierdzające, że rdzeń gospodarki kurczy się do zbioru równowag Walrasa , gdy liczba agentów wzrasta do nieskończoności.
To znaczy spośród wszystkich możliwych wyników, które mogą wynikać z wolnorynkowej wymiany lub barteru między grupami ludzi, podczas gdy dokładne miejsce ostatecznego rozliczenia (ostatecznego podziału dóbr) między stronami nie jest jednoznacznie określone, ponieważ liczba handlarzy rośnie , zbiór wszystkich możliwych rozliczeń końcowych zbiega się do zbioru równowag walrasowskich.
Intuicyjnie można to interpretować jako stwierdzenie, że wraz ze wzrostem gospodarki agenci coraz częściej zachowują się tak, jakby byli agentami cenotwórczymi, nawet jeśli mają moc negocjowania.
Edgeworth (1881) wysunął hipotezę twierdzenia i dostarczył większości niezbędnej intuicji oraz posunął się w pewnym stopniu w kierunku jego dowodu. Dowody formalne zostały przedstawione przy różnych założeniach przez Debreu i Scarf (1963) oraz Aumanna (1964), oba udowodnione w warunkach ostrzejszych niż zakładał Edgeworth. Debreu i Scarf rozważali przypadek „ekonomii repliki”, w której istnieje skończona liczba typów agentów, a agenci dodani do gospodarki, aby uczynić ją „dużą”, są tego samego typu iw takich samych proporcjach, jak ci, którzy już w nim są. Wynik Aumanna opierał się na istnieniu kontinuum agentów .
Rdzeń gospodarki
Rdzeniem gospodarki jest koncepcja z teorii gier kooperacyjnych zdefiniowana jako zbiór możliwych alokacji w gospodarce, których nie można ulepszyć podzbiorem zbioru konsumentów gospodarki (koalicja) . W przypadku gospodarek równowagi ogólnej zazwyczaj rdzeń nie jest pusty (istnieje co najmniej jedna wykonalna alokacja), ale jest również „duży” w tym sensie, że może istnieć kontinuum wykonalnych alokacji, które spełniają wymagania. Przypuszczenie zasadniczo stwierdza, że jeśli liczba agentów jest również „duża”, to jedyne alokacje w rdzeniu są dokładnie tym, co wyprodukowałby konkurencyjny rynek . Jako taka, przypuszczenie to jest postrzegane jako dostarczające pewnych podstaw teorii gier dla zwykłego założenia teorii równowagi ogólnej dotyczącej podmiotów przyjmujących ceny. W szczególności oznacza to, że w „dużej” gospodarce ludzie zachowują się tak, jakby byli cenobiorcami, mimo że teoretycznie mają pełną władzę ustalania cen i renegocjowania swoich transakcji. Stąd fikcyjny walrasowski licytator ogólnej równowagi, choć ściśle mówiąc całkowicie nierealistyczny, może być postrzegany jako „skrót” do uzyskania właściwej odpowiedzi.
Ilustracja, gdy są tylko dwa towary
Francis Ysidro Edgeworth po raz pierwszy opisał to, co później stało się znane jako twierdzenie graniczne w swojej książce Mathematical Psychics (1881). Użył wariantu tego, co jest obecnie znane jako pudełko Edgewortha (z ilościami będącymi przedmiotem obrotu, a nie posiadanymi ilościami, na odpowiednich osiach), aby przeanalizować handel między grupami handlowców o różnej wielkości. Ogólnie stwierdził, że „umowa bez konkurencji jest nieokreślona, umowa z konkurencją doskonałą jest doskonale określona, [a] umowa z mniej lub bardziej doskonałą konkurencją jest mniej lub bardziej nieokreślona”.
Handel bez konkurencji
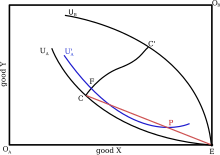
Jeśli handel dwoma towarami X i Y odbywa się między pojedynczą parą handlowców A i B, potencjalne wyniki tego handlu można przedstawić w ramce Edgewortha ( Rysunek 1 ). Na tym diagramie A i B początkowo posiadają odpowiednio cały zapas X i Y (punkt E). Linie U(a) i U(b) to krzywe obojętności A i B, które przechodzą przez punkty reprezentujące kombinacje dóbr, które dają użyteczność równą ich początkowemu zasobowi. Ponieważ zakłada się tutaj, że handel nie jest oparty na przymusie, żaden z handlowców nie zgodzi się na ostateczną ugodę, która pozostawi ich w gorszej sytuacji niż na początku, a zatem U(a) i U(b) reprezentują zewnętrzne granice możliwych rozliczeń. Edgeworth wykazał, że handlowcy ostatecznie dotrą do punktu na krzywej kontraktu (między C a C') poprzez stylizowany proces negocjacji, który jest nazywany procesem rekontraktowania. Ponieważ żadna osoba nie może poprawić sytuacji bez pogorszenia sytuacji drugiej w punktach na krzywej kontraktu, gdy handlowcy zgadzają się na rozliczenie w punkcie na niej, jest to ostateczne rozliczenie. Nie można dokładnie określić, gdzie nastąpi ostateczne rozliczenie na krzywej kontraktu. Będzie to zależeć od procesu negocjacji między dwiema osobami; strona, która jest w stanie uzyskać przewagę w negocjacjach, będzie mogła uzyskać lepszą cenę za swoje towary, a tym samym uzyskać większe zyski z handlu .
To było kluczowe odkrycie Edgewortha – wynik handlu między dwiema osobami można przewidzieć w pewnym zakresie, ale dokładny wynik jest nieokreślony. To odkrycie zostało (błędnie) zakwestionowane przez Alfreda Marshalla [ potrzebne źródło ] , a dyskusje między nimi na ten temat są znane jako kontrowersje barterowe.
Handluj z mniej niż doskonałą konkurencją
Załóżmy, że do tej początkowej pary dodaje się jedną dodatkową parę identycznych handlowców. Ponieważ ci nowi inwestorzy są identyczni z pierwszą parą, to samo pole Edgewortha może być użyte do analizy wymiany. Aby zbadać nowe zewnętrzne granice handlu, Edgeworth rozważył sytuację, w której handel odbywa się na granicy handlu między dwiema osobami (punkt C lub C' na rysunku 2 ). Gdyby handel miał miejsce w punkcie C, jeden z B (powiedzmy B(1)) otrzymałby wszystkie zyski z handlu. Osoba A, która handluje z B(1) (powiedzmy A(1)), ma teraz mieszankę towarów X i Y, którą może handlować z A(2). Ponieważ dwa A są identyczne, zgodzą się podzielić równo między siebie swoje fundusze potransakcyjne, umieszczając je w punkcie P na rysunku 2 , co daje im wyższą użyteczność niż uzyskaliby w innym przypadku (krzywa obojętności U'(a) zamiast U(a)). B(2) ma teraz okazję i silną motywację, aby oferować A lepszą cenę za swoje towary i handlować z nimi po tej cenie, pozostawiając B(1) na lodzie. Ten proces konkurowania ze sobą podmiotów B w celu zaoferowania podmiotom A lepszej ceny będzie trwał do momentu, gdy podmioty A staną się obojętne między handlem po cenie P a handlem po krzywej kontraktu (Rysunek 3 ) . To samo rozumowanie można zastosować do przypadku, w którym A(1) początkowo otrzymuje wszystkie zyski z handlu i można wykazać, że najbardziej zewnętrzna granica określona przez U(b) również przesunie się do wewnątrz. Nazywa się to kurczącym się rdzeniem rynku – w miarę dodawania dodatkowej pary handlowców możliwy zakres transakcji kurczy się.
Jeśli dodana zostanie trzecia para traderów, rdzeń rynku dalej się kurczy. Jeśli handel odbywa się na granicy, na której B(1) uzyskuje wszystkie zyski z handlu, punkt P znajduje się teraz w dwóch trzecich drogi wzdłuż linii EC. Poprawia to siłę przetargową A, którzy są w stanie wejść na wyższą krzywą obojętności, gdy B konkurują o handel z nimi. Zewnętrzną granicę ostatecznego rozliczenia w przypadku wielu par handlowców można uogólnić ( Rysunek 4 ), gdzie K = (n-1)/n.
Handel z doskonałą konkurencją
Jeśli jest wystarczająca liczba handlowców, rdzeń rynku skurczy się tak, że punkt ostatecznego rozliczenia jest doskonale określony ( Rysunek 5 ). Ten punkt jest równy równowadze przyjmowania cen , w której zakłada się, że odbywa się handel w modelach doskonałej konkurencji .
Uogólnienie
Ta analiza może zostać zmodyfikowana, aby uwzględnić traderów, którzy nie są identyczni lub których motywacje nie są czysto egoistyczne, a także sytuację, w której jedna grupa traderów jest większa od drugiej. Jeśli inwestorzy są heterogeniczni, punkt P nie będzie odzwierciedlał handlu „podziel różnicę” między grupą handlowców, a zewnętrzny limit handlu określony przez ten punkt zostanie odpowiednio zmodyfikowany. Jeśli użyteczność jednego tradera wpływa na użyteczność innego (tj. ten ostatni nie jest samolubny), wówczas związana z tym granica krzywej kontraktu zmniejszy się do wewnątrz, wykluczając najbardziej niesprawiedliwe transakcje. Jeśli grupy traderów są różnej wielkości, zewnętrzne granice krzywej kontraktu nie zmniejszą się o taką samą wartość.
Implikacje
Istnieją dwie główne implikacje twierdzenia granicznego. Po pierwsze, końcowy wynik handlu między małymi grupami ludzi jest nieokreślony i jest określany przez czynniki pozaekonomiczne dla Edgewortha. Po drugie, ekwiwalent równowagi przyjmowania cen może wynikać z konkurencji między bardzo dużymi grupami handlowców w procesie ponownego zawierania umów. Ten punkt równowagi nie może zostać przesunięty przez grupy handlowców działających w zmowie w celu uzyskania zysków z handlu dla siebie, ponieważ inni handlowcy zawsze będą mieli motywację do pozostawienia grupy na lodzie. Stanowi to uzasadnienie dla zakładania zachowań związanych z przyjmowaniem cen w pewnych sytuacjach, mimo że wyjaśnienia, w jaki sposób może dojść do sytuacji polegającej na przyjmowaniu cen (takie jak tatonnement ) są wyraźnie niewiarygodne [ potrzebne źródło ] .
Krytyka
W dużym stopniu wynik nieokreśloności opiera się na założeniu, że wyniki negocjacji są nieokreślone lub przynajmniej nie należą do sfery spekulacji ekonomicznych. Współczesne postępy w teorii gier , takie jak te opracowane przez Johna Nasha , podważają to założenie i wyprowadzają stabilne równowagi (takie jak równowaga Nasha ) w skomplikowanych sytuacjach przetargowych. Co więcej, proponowany przez Edgewortha proces ponownego zawierania umów jest wysoce stylizowany i obejmuje handlowców uzyskujących informacje poprzez bezkosztowe zawieranie, zrywanie i ponowne zawieranie między sobą umów. Marshall ostro skrytykował Edgewortha w tej kwestii. Jeśli proces ponownego zawierania umów nie wyjaśnia zachowania w świecie rzeczywistym, wówczas wniosek, że punkt równowagi przy ustalaniu ceny zostanie osiągnięty przez konkurencyjnych handlowców, niekoniecznie będzie prawdziwy [ potrzebne źródło ] .