Zasada zagłady

John Conway , wynalazca algorytmu Doomsday

Zasada Doomsday , algorytm Doomsday lub metoda Doomsday to algorytm określania dnia tygodnia dla danej daty. Zapewnia wieczny kalendarz , ponieważ kalendarz gregoriański porusza się w cyklach 400-letnich. Algorytm obliczeń mentalnych został opracowany przez Johna Conwaya w 1973 roku, czerpiąc inspirację z algorytmu wiecznego kalendarza Lewisa Carrolla . Wykorzystuje to, że każdy rok ma określony dzień tygodnia, w którym przypadają pewne łatwe do zapamiętania daty, zwane dniami zagłady ; na przykład ostatni dzień lutego, 4/4, 6/6, 8/8, 10/10 i 12/12 przypadają w tym samym dniu tygodnia w dowolnym roku. Zastosowanie algorytmu Doomsday obejmuje trzy kroki: określenie dnia zakotwiczenia dla stulecia, obliczenie dnia zakotwiczenia dla roku z jednego dla stulecia oraz wybranie najbliższej daty spośród tych, które zawsze przypadają na dzień zagłady, np. 4/4 i 6/6 i policz liczbę dni ( modulo 7 ) między tą datą a daną datą, aby dojść do dnia tygodnia. Technika ta dotyczy zarówno kalendarza gregoriańskiego , jak i juliańskiego , chociaż ich dni zagłady to zwykle różne dni tygodnia.

Algorytm jest na tyle prosty, że można go obliczyć w pamięci. Conway zwykle potrafił udzielić poprawnej odpowiedzi w mniej niż dwie sekundy. Aby poprawić swoją szybkość, ćwiczył swoje obliczenia kalendarzowe na swoim komputerze, który został zaprogramowany tak, aby przepytywał go losowymi datami za każdym razem, gdy się logował.

Dni zakotwiczenia dla niektórych współczesnych lat

Dniem zakotwiczenia Dnia Zagłady w bieżącym roku w kalendarzu gregoriańskim (2023) jest wtorek. Dla kilku innych współczesnych lat:

**Dni zakotwiczone w kalendarzu gregoriańskim**
pon.	wt.	Poślubić.	czw.	pt.	sob.	Słońce.
1701	1702	1703	→	1704	1705	1706
1707	→	1708	1709	1710	1711	→
1712	1713	1714	1715	→	1716	1717
1718	1719	→	1720	1721	1722	1723
→	1724	1725	1726	1727	→	1728
1729	1730	1731	→	1732	1733	1734
1735	→	1736	1737	1738	1739	→
1740	1741	1742	1743	→	1744	1745
1746	1747	→	1748	1749	1750	1751
→	1752	1753	1754	1755	→	1756
1757	1758	1759	→	1760	1761	1762
1763	→	1764	1765	1766	1767	→
1768	1769	1770	1771	→	1772	1773
1774	1775	→	1776	1777	1778	1779
→	1780	1781	1782	1783	→	1784
1785	1786	1787	→	1788	1789	1790
1791	→	1792	1793	1794	1795	→
1796	1797	1798	1799	1800	1801	1802
1803	→	1804	1805	1806	1807	→
1808	1809	1810	1811	→	1812	1813
1814	1815	→	1816	1817	1818	1819
→	1820	1821	1822	1823	→	1824
1825	1826	1827	→	1828	1829	1830
1831	→	1832	1833	1834	1835	→
1836	1837	1838	1839	→	1840	1841
1842	1843	→	1844	1845	1846	1847
→	1848	1849	1850	1851	→	1852
1853	1854	1855	→	1856	1857	1858
1859	→	1860	1861	1862	1863	→
1864	1865	1866	1867	→	1868	1869
1870	1871	→	1872	1873	1874	1875
→	1876	1877	1878	1879	→	1880
1881	1882	1883	→	1884	1885	1886
1887	→	1888	1889	1890	1891	→
1892	1893	1894	1895	1896	→	1897
1898	1899	1900	1901	1902	1903	→
1904	1905	1906	1907	→	1908	1909
1910	1911	→	1912	1913	1914	1915
→	1916	1917	1918	1919	→	1920
1921	1922	1923	→	1924	1925	1926
1927	→	1928	1929	1930	1931	→
1932	1933	1934	1935	→	1936	1937
1938	1939	→	1940	1941	1942	1943
→	1944	1945	1946	1947	→	1948
1949	1950	1951	→	1952	1953	1954
1955	→	1956	1957	1958	1959	→
1960	1961	1962	1963	→	1964	1965
1966	1967	→	1968	1969	1970	1971
→	1972	1973	1974	1975	→	1976
1977	1978	1979	→	1980	1981	1982
1983	→	1984	1985	1986	1987	→
1988	1989	1990	1991	→	1992	1993
1994	1995	→	1996	1997	1998	1999
→	2000	2001	2002	2003	→	2004
2005	2006	2007	→	2008	2009	2010
2011	→	2012	2013	2014	2015	→
2016	2017	2018	2019	→	2020	2021
2022	2023	→	2024	2025	2026	2027
→	2028	2029	2030	2031	→	2032
2033	2034	2035	→	2036	2037	2038
2039	→	2040	2041	2042	2043	→
2044	2045	2046	2047	→	2048	2049
2050	2051	→	2052	2053	2054	2055
→	2056	2057	2058	2059	→	2060
2061	2062	2063	→	2064	2065	2066
2067	→	2068	2069	2070	2071	→
2072	2073	2074	2075	→	2076	2077
2078	2079	→	2080	2081	2082	2083
→	2084	2085	2086	2087	→	2088
2089	2090	2091	→	2092	2093	2094
2095	→	2096	2097	2098	2099	2100

Tabelę wypełnia się poziomo, z pominięciem jednej kolumny dla każdego roku przestępnego. Ta tabela zmienia się co 28 lat, z wyjątkiem kalendarza gregoriańskiego w latach, które są wielokrotnością 100 (takie jak 1900 i 2100, które nie są latami przestępnymi), które nie są również wielokrotnością 400 (jak 2000, który wciąż jest rokiem przestępnym) . Pełny cykl to 28 lat (1461 tygodni) w kalendarzu juliańskim, 400 lat (20871 tygodni) w kalendarzu gregoriańskim.

Niezapomniane daty, które zawsze kończą się w dniu Sądu Ostatecznego

Można znaleźć dzień tygodnia o określonej dacie kalendarzowej, używając jako punktu odniesienia pobliskiego dnia zagłady. Aby w tym pomóc, poniżej znajduje się lista łatwych do zapamiętania dat dla każdego miesiąca, które zawsze lądują w dniu zagłady.

Jak wspomniano powyżej, ostatni dzień lutego określa dzień zagłady. W styczniu 3 stycznia jest dniem zagłady w latach zwykłych, a 4 stycznia dniem zagłady w latach przestępnych, który można zapamiętać jako „trzeci w ciągu 3 lat w 4, a czwarty w 4 roku”. Za marzec można zapamiętać pseudodatę „ marca 0 ”, która odnosi się do dnia poprzedzającego 1 marca, czyli ostatniego dnia lutego.

Dla miesięcy od kwietnia do grudnia, parzyste miesiące są objęte podwójnymi datami 4/4, 6/6, 8/8, 10/10 i 12/12, z których wszystkie przypadają na dzień sądu ostatecznego. Miesiące nieparzyste można zapamiętać za pomocą mnemonika „Pracuję od 9 do 5 w godzinach 7-11 ”, tj. true zarówno dla konwencji dzień/miesiąc, jak i miesiąc/dzień).

Kilka dobrze znanych dat, takich jak Dzień liczby Pi , Dzień Niepodległości w Stanach Zjednoczonych i początek hiszpańskiej wojny domowej , również przypadają co roku w dni zagłady. Poniższy wykres zawiera tylko mnemoniki uwzględnione w wymienionych źródłach.

Miesiąc	Pamiętna data	Dzień miesiąca	Mnemoniczny	Pełna lista dni
Styczeń	3 stycznia (lata zwykłe), 4 stycznia (lata przestępne)	1/3 LUB 1/4 (1/31 LUB 1/32)	3. 3 lata w 4. i 4. w 4. (lub: ostatni dzień stycznia, udając, że lata przestępne mają 32 stycznia)	3, 10, 17, 24, 31 LUB 4, 11, 18, 25, 32
Luty	28 lutego (lata zwykłe), 29 lutego (lata przestępne)	2/28 LUB 2/29	ostatni dzień lutego	7, 14, 21, 28 LUB 1, 8, 15, 22, 29
Marsz	„ 0 marca ”	3/0	ostatni dzień lutego	0, 7, 14, 21, 28
Kwiecień	4 kwietnia	4/4	4/4 , 6/6, 8/8, 10/10, 12/12	4, 11, 18, 25
Móc	9 maja	5/9	9-do-5 na 7-11	2, 9, 16, 23, 30
Czerwiec	6 czerwca	6/6	4/4, 6/6 , 8/8, 10/10, 12/12	6, 13, 20, 27
Lipiec	11 lipca	7/11	9-do-5 na 7-11	4, 11, 18, 25
Sierpień	8 sierpnia	8/8	4/4, 6/6, 8/8 , 10/10, 12/12	1, 8, 15, 22, 29
Wrzesień	5 września	9/5	9-do-5 na 7-11	5, 12, 19, 26
Październik	10 października	10/10	4/4, 6/6, 8/8, 10/10 , 12/12	3, 10, 17, 24, 31
Listopad	7 listopada	11/7	9-do-5 na 7-11	7, 14, 21, 28
Grudzień	12 grudnia	12/12	4/4, 6/6, 8/8, 10/10, 12/12	5, 12, 19, 26

Ponieważ dzień zagłady dla danego roku jest bezpośrednio powiązany z dniami powszednimi dat w okresie od marca do lutego następnego roku, należy rozróżnić lata zwykłe i lata przestępne dla stycznia i lutego tego samego roku.

Miesiąc	M	Dzień Sądu Ostatecznego
styczeń	1	3/4	C/L	PŁYTA CD
luty	2	0/1	C/L	PŁYTA CD
Zniszczyć	3	7/0	M + 4	dzień C
Móc	5	9
lipiec	7	11
wrzesień	9	5	M-4
listopad	11	7
styczeń	13	9/2		Urodziny
kwiecień	4	4	M	dzień C
czerwiec	6	6
sierpień	8	8
październik	10	10
grudzień	12	12
luty	14	13/-1	M-1	Urodziny

Styczeń i luty można traktować jako dwa ostatnie miesiące poprzedniego roku.

Przykład

Aby dowiedzieć się, który dzień tygodnia przypada na Boże Narodzenie w 2021 roku, wykonaj następujące czynności: w roku 2021 dzień zagłady wypada w niedzielę. Ponieważ 12 grudnia to dzień zagłady, 25 grudnia, przypadający po trzynastu dniach (dwa tygodnie mniej dziennie), wypada w sobotę. Boże Narodzenie to zawsze dzień poprzedzający koniec świata. Ponadto 4 lipca ( Dzień Niepodległości Stanów Zjednoczonych ) jest zawsze dniem zagłady, podobnie jak Halloween (31 października), Dzień Pi (14 marca) i drugi dzień świąt (26 grudnia).

Mnemoniczne nazwy dni tygodnia

Ponieważ ten algorytm polega na traktowaniu dni tygodnia jak liczb modulo 7, John Conway zasugerował myślenie o dniach tygodnia jako „Noneday” lub „Sansday” (dla niedzieli), „Oneday”, „Twosday”, „Treblesday”, „ Czterodniowy”, „Pięciodniowy” i „Sześć dziennie”, aby przywołać relację liczba-dzień bez konieczności liczenia ich w głowie.

dzień tygodnia	Numer indeksu	Mnemoniczny
Niedziela	0	Żaden dzień ani sylwester
Poniedziałek	1	Pewnego dnia
Wtorek	2	dwa dni
Środa	3	Treblesday
Czwartek	4	Czwarty dzień
Piątek	5	Pięć dni
Sobota	6	Sześć dziennie

Niektóre języki, takie jak języki słowiańskie , chiński , grecki , portugalski , galicyjski i hebrajski , opierają niektóre nazwy dni tygodnia na porządku pozycyjnym . Słowianie i Chińczycy zgadzają się z powyższą tabelą; pozostałe wymienione języki liczą się od niedzieli jako pierwszego dnia.

Znalezienie rocznego dnia kotwicy

Najpierw weź dzień kotwicy stulecia. Dla celów zasady dnia zagłady stulecie zaczyna się od '00, a kończy na '99. Poniższa tabela przedstawia dzień zakotwiczenia stuleci 1600–1699, 1700–1799, 1800–1899, 1900–1999, 2000–2099, 2100–2199 i 2200–2299.

Wiek	Dzień kotwicy	Mnemoniczny	Indeks (dzień tygodnia)
1600-1699	Wtorek	—	2 (dwa dni)
1700-1799	Niedziela	—	0 (brak dnia)
1800–1899	Piątek	—	5 (pięć dni)
1900–1999	Środa	We-in-dis-day (większość żyjących ludzi urodziła się w tym stuleciu)	3 (Dzień potrójny)
2000–2099	Wtorek	Y-Tue-K lub Twos-day ( rok 2000 był na czele tego stulecia)	2 (dwa dni)
2100–2199	Niedziela	Dwudziesty jeden dzień to niedziela (2100 to początek następnego stulecia)	0 (brak dnia)
2200–2299	Piątek	—	5 (pięć dni)

Dla kalendarza gregoriańskiego:

Wzór matematyczny

5 \times (c mod 4) mod 7 +

wtorek = kotwica.

Niech

jeśli

r = c mod 4

jeśli

r = 0

to kotwica = wtorek

jeśli

r = 1

to kotwica = niedziela

r

= 2

to kotwica = piątek

jeśli

r = 3

to kotwica = środa

Dla kalendarza juliańskiego:

6 c mod 7 +

niedziela = kotwica.

Uwaga: $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} c = ⌊ rok / 100 ⌋$ .

Następnie znajdź roczny dzień zakotwiczenia. Aby to osiągnąć według Conwaya:

Podziel ostatnie dwie cyfry roku (nazwijmy to $y$ ) przez 12 i niech $a$ będzie dolną częścią ilorazu .
Niech $b$ będzie resztą tego samego ilorazu.
Podziel tę resztę przez 4 i niech $c$ będzie dolną częścią ilorazu.
Niech $d$ będzie sumą trzech liczb ( $d = a + b + c$ ). (Znowu tutaj można podzielić przez siedem i wziąć resztę. Ta liczba jest, jak trzeba, równoważna sumie dwóch ostatnich cyfr roku wziętej łącznie plus dolna część tych wspólnych cyfr podzielona przez cztery.)
Policz w przód określoną liczbę dni ( $d$ lub resztę z $d / 7$ ) od dnia zakotwiczenia, aby uzyskać jeden rok.

{\ Displaystyle {\ rozpocząć {macierz} \ lewo ({

Dla roku XX-wiecznego 1966 np.:

\ Displaystyle {\ rozpocząć {macierz} \ lewo ({\ lewo \ lfloor {\ Frac {66} {12}} \ prawo \ rfloor + 66 {\ bmod {1}} 2+ \left\lfloor {\frac {66{\bmod {1}}2}{4}}\right\rfloor}\right){\bmod {7}}+{\rm {środa}}&=&\left (5+6+1\right){\bmod {7}}+{\rm {środa}}\\\ &=&{\rm {poniedziałek}}\end{macierz}}}

Jak opisano w punkcie 4 powyżej, jest to równoważne z:

\ Displaystyle {\ begin{matrix}\left({66+\left\lfloor {\frac {66}{4}}\right\rfloor}\right){\bmod {7}}+{\rm {środa}}&=& \left(66+16\right){\bmod {7}}+{\rm {środa}}\\\ &=&{\rm {poniedziałek}}\end{macierz}}}

Tak więc dzień zagłady w 1966 roku wypadł w poniedziałek.

Podobnie dzień zagłady w 2005 roku wypada w poniedziałek:

{\ Displaystyle \ lewo ({\ lewo \ lfloor {\

Dlaczego to działa

Zasada zagłady

Obliczenie dnia zakotwiczenia dnia zagłady skutecznie oblicza liczbę dni między dowolną datą w roku bazowym a tą samą datą w bieżącym roku, a następnie bierze resztę modulo 7. Kiedy obie daty następują po dniu przestępnym (jeśli istnieje), różnica wynosi zaledwie $365 y + y / 4$ (w zaokrągleniu w dół). Ale 365 równa się 52 × 7 + 1, więc po wzięciu reszty otrzymujemy właśnie

{\ Displaystyle \ lewo (y + \ lewo \ lfloor {\ Frac {y} {4}} \ prawo \ rfloor \ prawo) {\ bmod {7}}.}

Daje to prostszą formułę, jeśli wygodnie jest podzielić duże wartości $y$ przez 4 i 7. Na przykład możemy obliczyć

{\ Displaystyle \ lewo (66+ \ lewo \ lfloor {\ Frac {66} {4}} \ prawo \ rfloor \right){\bmod {7}}=(66+16){\bmod {7}}=82{\bmod {7}}=5}

co daje taką samą odpowiedź jak w powyższym przykładzie.

Tam, gdzie pojawia się 12, wzór $(y + ⌊ y / 4 ⌋) mod 7$ prawie powtarza się co 12 lat. Po 12 latach otrzymujemy $(12 + 12 / 4) mod 7 = 15 mod 7 = 1$ . Jeśli zastąpimy $y$ przez $y mod 12$ , odrzucamy ten dodatkowy dzień; ale dodanie z powrotem w $⌊ y / 12 ⌋$ kompensuje ten błąd, dając ostateczną formułę.

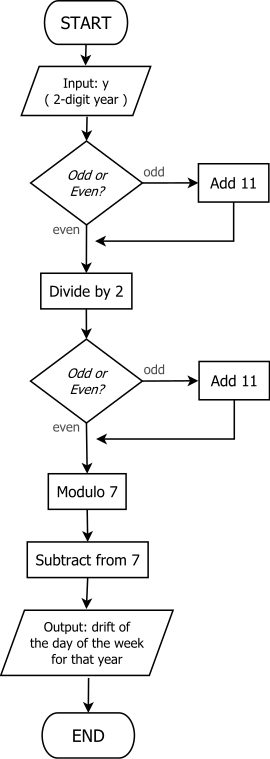
Metoda „nieparzysty + 11”.

Prosty schemat blokowy przedstawiający metodę Odd+11 do obliczania dnia kotwicy

Prostsza metoda znajdowania dnia kotwicy roku została odkryta w 2010 roku przez Chamberlaina Fonga i Michaela K. Waltersa i opisana w ich artykule przesłanym na 7. Międzynarodowy Kongres Matematyki Przemysłowej i Stosowanej (2011). Nazywana metodą „nieparzyste + 11”, jest równoważna z obliczeniami

{\ Displaystyle \ lewo (y + \ lewo \ lfloor {\ Frac {y} {4}} \ prawo \ rfloor \ prawo) {\ bmod {7}}}

.

Dobrze nadaje się do obliczeń umysłowych, ponieważ nie wymaga dzielenia przez 4 (lub 12), a procedura jest łatwa do zapamiętania ze względu na wielokrotne użycie zasady „nieparzysty + 11”. Co więcej, dodawanie przez 11 jest bardzo łatwe do wykonania mentalnie w arytmetyce o podstawie 10 .

Rozszerzając to, aby uzyskać dzień zakotwiczenia, procedura jest często opisywana jako gromadzenie bieżącej sumy $T$ w sześciu krokach, jak następuje:

Niech $T$ będzie dwiema ostatnimi cyframi roku.
Jeśli $T$ jest nieparzyste, dodaj 11.
Niech teraz $T = T / 2$ .
Jeśli $T$ jest nieparzyste, dodaj 11.
Niech teraz $T = 7 - (T mod 7)$ .
Odliczaj w przód $T$ dni od dnia zakotwiczenia stulecia, aby uzyskać roczny dzień zakotwiczenia.

Stosując tę metodę na przykład do roku 2005, opisane kroki byłyby następujące:

$T = 5$
$T = 5 + 11 = 16$ (dodanie 11, ponieważ $T$ jest nieparzyste)
$T = 16 / 2 = 8$
$T = 8$ (nic nie rób, ponieważ $T$ jest parzyste)
$T = 7 - (8 mod 7) = 7 - 1 = 6$
Dzień zagłady 2005 = 6 + wtorek = poniedziałek

Wyraźna formuła metody nieparzystej + 11 to:

{\ Displaystyle 7- \ lewo [{\ Frac {y + 11 (y \, { \bmod {2}})}{2}}+11\left({\frac {y+11(y\,{\bmod {2}})}{2}}{\bmod {2}}\right )\right]{\bmod {7}}}

.

Chociaż to wyrażenie wygląda na zniechęcające i skomplikowane, w rzeczywistości jest proste ze względu na wspólne podwyrażenie $y + 11(y mod 2) / 2$ , które wystarczy obliczyć tylko raz.

Za każdym razem, gdy potrzebne jest dodanie 11, odjęcie 17 daje równoważne wyniki. Chociaż odejmowanie 17 może wydawać się trudniejsze do wykonania mentalnie niż dodawanie 11, istnieją przypadki, w których odejmowanie 17 jest łatwiejsze, zwłaszcza gdy liczba jest liczbą dwucyfrową, która kończy się na 7 (na przykład 17, 27, 37, ..., 77, 87 i 97).

Korespondencja z listem Dominika

Doomsday jest powiązany z dominującą literą roku w następujący sposób.

Dzień Sądu Ostatecznego	List Dominika
Dzień Sądu Ostatecznego	Wspólny rok	Rok przestępny
Niedziela	C	DC
Poniedziałek	B	CB
Wtorek	A	BA
Środa	G	AG
Czwartek	F	GF
Piątek	mi	FE
Sobota	D	ED

Poszukaj w poniższej tabeli litery dominującej (DL).

Setki lat		DL _	Pozostałe cyfry roku				#
Julian (r ÷ 7)	gregoriański (r ÷ 4)	DL _	Pozostałe cyfry roku				#
r5 19	16 20 r0	A	00 06 17 23	28 34 45 51	56 62 73 79	84 90	0
r4 18	15 19 r3	G	01 07 12 18	29 35 40 46	57 63 68 74	85 91 96	1
r3 17	Nie dotyczy	F	02 13 19 24	30 41 47 52	58 69 75 80	86 97	2
r2 16	18 22 r2	mi	03 08 14 25	31 36 42 53	59 64 70 81	87 92 98	3
r1 15	Nie dotyczy	D	09 15 20 26	37 43 48 54	65 71 76 82	93 99	4
r0 14	17 21 r1	C	04 10 21 27	32 38 49 55	60 66 77 83	88 94	5
r6 13	Nie dotyczy	B	05 11 16 22	33 39 44 50	61 67 72 78	89 95	6

W roku 2023 dominującą literą jest A - 0 = A ^{[ wymaga aktualizacji ]} .

Przegląd wszystkich Doomsdays

Miesiąc	Daktyle	Numery tygodni *
styczeń (lata zwykłe)	3, 10, 17, 24, 31	1–5
styczeń (lata przestępne)	4, 11, 18, 25	1–4
luty (lata zwykłe)	7, 14, 21, 28	6–9
luty (lata przestępne)	1, 8, 15, 22, 29	5–9
Marsz	7, 14, 21, 28	10–13
Kwiecień	4, 11, 18, 25	14-17
Móc	2, 9, 16, 23, 30	18–22
Czerwiec	6, 13, 20, 27	23-26
Lipiec	4, 11, 18, 25	27–30
Sierpień	1, 8, 15, 22, 29	31–35
Wrzesień	5, 12, 19, 26	36–39
Październik	3, 10, 17, 24, 31	40–44
Listopad	7, 14, 21, 28	45–48
Grudzień	5, 12, 19, 26	49–52

* W latach przestępnych $n-$ ty dzień zagłady przypada na tydzień ISO $n$ . W zwykłych latach dzień po $n-$ tym dniu zagłady przypada na tydzień $n$ . Tak więc w zwykłym roku liczba tygodni w samym dniu zagłady jest o jeden mniejsza, jeśli jest to niedziela, czyli w zwykłym roku rozpoczynającym się w piątek .

Formuła komputerowa na dzień zakotwiczenia w roku

Do użytku komputerowego wygodne są następujące wzory na dzień zakotwiczenia w roku.

Dla kalendarza gregoriańskiego:

{ \ Displaystyle {\ mbox {dzień kotwicy}} = {\ mbox {wtorek}} + y + \ lewo \ lfloor {\ Frac {y} {4}} \ prawo \ rfloor - \ lewo \ lfloor {\ frac {y} 100}}\right\rfloor +\left\lfloor {\frac {y}{400}}\right\rfloor ={\mbox{wtorek}}+5\razy (y{\bmod {4}})+4 \razy (y{\bmod {1}}00)+6\razy (y{\bmod {4}}00)}

Na przykład dzień zagłady 2009 to sobota według kalendarza gregoriańskiego (obecnie akceptowanego kalendarza), ponieważ

{\ Displaystyle {\ mbox {sobota (6)}} {\ bmod {7}} = { \mbox{wtorek (2)}}+2009+\left\lfloor {\frac {2009}{4}}\right\rfloor -\left\lfloor {\frac {2009}{100}}\right\rfloor + \left\lfloor {\frac {2009}{400}}\right\rfloor}

Jako inny przykład, dniem zagłady 1946 jest czwartek, ponieważ

{\ Displaystyle {\ mbox {czwartek (4)}} {\ bmod {7}} = { \mbox{wtorek (2)}}+1946+\left\lfloor {\frac {1946}{4}}\right\rfloor -\left\lfloor {\frac {1946}{100}}\right\rfloor + \left\lfloor {\frac {1946}{400}}\right\rfloor}

Dla kalendarza juliańskiego:

{\ Displaystyle {\ mbox {dzień kotwicy}} = {\ mbox {niedziela}} + y + \left\lfloor {\frac {y}{4}}\right\rfloor ={\mbox{niedziela}}+5\razy (y{\bmod {4}})+3\razy (y{\bmod { 7}})}

Formuły odnoszą się również do proleptycznego kalendarza gregoriańskiego i proleptycznego kalendarza juliańskiego . Używają funkcji podłogi i astronomicznej numeracji lat dla lat przed naszą erą.

Dla porównania zobacz obliczenie liczby dni juliańskich .

400-letni cykl dni zakotwiczenia

wieków juliańskich				-1600J -900J -200J 500J 1200J 1900J 2600J 3300J	-1500J -800J -100J 600J 1300J 2000J 2700J 3400J	-1400J -700J 0J 700J 1400J 2100J 2800J 3500J	-1300J -600J 100J 800J 1500J 2200J 2900J 3600J	-1200J -500J 200J 900J 1600J 2300J 3000J 3700J	-1100J -400J 300J 1000J 1700J 2400J 3100J 3800J	-1000J -300J 400J 1100J 1800J 2500J 3200J 3900J
wieków gregoriańskich Lata				0 -1600 -1200 -800 -400 400 800 1200 1600 2000 2400 2800 3200 3600		-1500 -1100 -700 -300 100 500 900 1300 1700 2100 2500 2900 3300 3700		-1400 -1000 -600 -200 200 600 1000 1400 1800 2200 2600 3000 3400 3800		-1300 -900 -500 -100 300 700 1100 1500 1900 2300 2700 3100 3500 3900
00	28	56	84	wt.	pon.	Słońce.	sob.	pt.	czw.	Poślubić.
01	29	57	85	Poślubić.	wt.	pon.	Słońce.	sob.	pt.	czw.
02	30	58	86	czw.	Poślubić.	wt.	pon.	Słońce.	sob.	pt.
03	31	59	87	pt.	czw.	Poślubić.	wt.	pon.	Słońce.	sob.
04	32	60	88	Słońce.	sob.	pt.	czw.	Poślubić.	wt.	pon.
05	33	61	89	pon.	Słońce.	sob.	pt.	czw.	Poślubić.	wt.
06	34	62	90	wt.	pon.	Słońce.	sob.	pt.	czw.	Poślubić.
07	35	63	91	Poślubić.	wt.	pon.	Słońce.	sob.	pt.	czw.
08	36	64	92	pt.	czw.	Poślubić.	wt.	pon.	Słońce.	sob.
09	37	65	93	sob.	pt.	czw.	Poślubić.	wt.	pon.	Słońce.
10	38	66	94	Słońce.	sob.	pt.	czw.	Poślubić.	wt.	pon.
11	39	67	95	pon.	Słońce.	sob.	pt.	czw.	Poślubić.	wt.
12	40	68	96	Poślubić.	wt.	pon.	Słońce.	sob.	pt.	czw.
13	41	69	97	czw.	Poślubić.	wt.	pon.	Słońce.	sob.	pt.
14	42	70	98	pt.	czw.	Poślubić.	wt.	pon.	Słońce.	sob.
15	43	71	99	sob.	pt.	czw.	Poślubić.	wt.	pon.	Słońce.
16	44	72		pon.	Słońce.	sob.	pt.	czw.	Poślubić.	wt.
17	45	73		wt.	pon.	Słońce.	sob.	pt.	czw.	Poślubić.
18	46	74		Poślubić.	wt.	pon.	Słońce.	sob.	pt.	czw.
19	47	75		czw.	Poślubić.	wt.	pon.	Słońce.	sob.	pt.
20	48	76		sob.	pt.	czw.	Poślubić.	wt.	pon.	Słońce.
21	49	77		Słońce.	sob.	pt.	czw.	Poślubić.	wt.	pon.
22	50	78		pon.	Słońce.	sob.	pt.	czw.	Poślubić.	wt.
23	51	79		wt.	pon.	Słońce.	sob.	pt.	czw.	Poślubić.
24	52	80		czw.	Poślubić.	wt.	pon.	Słońce.	sob.	pt.
25	53	81		pt.	czw.	Poślubić.	wt.	pon.	Słońce.	sob.
26	54	82		sob.	pt.	czw.	Poślubić.	wt.	pon.	Słońce.
27	55	83		Słońce.	sob.	pt.	czw.	Poślubić.	wt.	pon.

Ponieważ w kalendarzu gregoriańskim jest 146 097 dni, czyli dokładnie 20 871 siedmiodniowych tygodni, w ciągu 400 lat dzień zakotwiczenia powtarza się co cztery stulecia. Na przykład dzień zakotwiczenia 1700-1799 jest taki sam jak dzień zakotwiczenia 2100-2199, czyli niedziela.

Pełny 400-letni cykl dni zagłady jest podany w sąsiedniej tabeli. Wieki dotyczą kalendarza gregoriańskiego i proleptycznego kalendarza gregoriańskiego , chyba że oznaczono je literą J jak Julian. Podkreślono gregoriańskie lata przestępne.

Lata ujemne używają astronomicznej numeracji lat . Rok 25 pne to -24, pokazany w kolumnie -100J (proleptyczny julian) lub -100 (proleptyczny gregoriański), w rzędzie 76.

**Częstotliwość gregoriańskiego dnia zagłady w 400-letnim cyklu na dzień tygodnia i rok**
	Niedziela	Poniedziałek	Wtorek	Środa	Czwartek	Piątek	Sobota	Całkowity
Lata nieprzestępne	43	43	43	43	44	43	44	303
Lata przestępne	13	15	13	15	13	14	14	97
Całkowity	56	58	56	58	57	57	58	400

Rok przestępny z poniedziałkiem jako dniem zagłady oznacza, że niedziela jest jednym z 97 dni pomijanych w ciągu 400 lat. Tak więc całkowita liczba lat z niedzielą jako dniem zagłady wynosi 71 minus liczba lat przestępnych z poniedziałkiem jako dniem zagłady itd. Od poniedziałku jako dnia zagłady jest pomijany 29 lutego 2000 r., A wzór dni przestępnych jest symetryczny względem tego dnia przestępnego, częstotliwości dni zagłady na dzień tygodnia (dodając lata zwykłe i przestępne) są symetryczne względem poniedziałku. Częstotliwości dni zagłady lat przestępnych w dni powszednie są symetryczne względem dnia zagłady 2000 roku, we wtorek.

Z powyższego można łatwo wywnioskować, jak często dany dzień wypada w dany dzień tygodnia (dla daty od 1 stycznia do 28 lutego należy odnieść ją do dnia zagłady poprzedniego roku).

Na przykład 28 lutego przypada jeden dzień po dniu zagłady z poprzedniego roku, więc jest to 58 razy we wtorek, czwartek i niedzielę itd. 29 lutego to dzień zagłady roku przestępnego, więc jest to 15 razy w poniedziałek i środę, itp.

Cykl 28-letni

Jeśli chodzi o częstotliwość dni zagłady w 28-letnim cyklu juliańskim, na każdy dzień tygodnia przypada 1 rok przestępny i 3 lata zwykłe, przy czym te ostatnie 6, 17 i 23 lata po pierwszym (czyli w odstępach 6, 11, 6 i 5 lat; nierównomiernie, bo po 12 latach dzień jest pomijany w ciągu dni zagłady). ^{[ potrzebne źródło ]} Ten sam cykl obowiązuje dla dowolnej daty od 1 marca przypadającej na określony dzień tygodnia.

Dla dowolnej daty do 28 lutego przypadającej w określony dzień tygodnia, 3 wspólne lata to 5, 11 i 22 lata po roku przestępnym, a więc w odstępach 5, 6, 11 i 6 lat. Zatem cykl jest taki sam, ale z 5-letnią przerwą po roku przestępnym zamiast przed nim.

Tak więc dla dowolnej daty z wyjątkiem 29 lutego odstępy między zwykłymi latami przypadającymi na dany dzień tygodnia wynoszą 6, 11, 11. Zobacz np. Na dole strony Rok wspólny rozpoczynający się w poniedziałek lata z przedziału 1906–2091.

29 lutego wypada w określony dzień powszedni, przypada tylko raz na 28 lat i jest to oczywiście rok przestępny.

kalendarz juliański

Kalendarz gregoriański jest obecnie dokładnie zgodny z wydarzeniami astronomicznymi, takimi jak przesilenia . W 1582 roku po raz pierwszy wprowadzono tę modyfikację kalendarza juliańskiego . Aby skorygować przesunięcie kalendarza, pominięto 10 dni, więc dzień zagłady przesunięto o 10 dni (tj. 3 dni): po czwartku 4 października (Julian, dzień zagłady to środa) nastąpił piątek 15 października (gregoriański, dzień zagłady to niedziela). Tabela zawiera lata kalendarza juliańskiego, ale algorytm dotyczy tylko gregoriańskiego i proleptycznego kalendarza gregoriańskiego.

Należy zauważyć, że kalendarz gregoriański nie został przyjęty we wszystkich krajach jednocześnie, więc przez wiele stuleci różne regiony używały różnych dat tego samego dnia.

Pełne przykłady

Przykład 1 (1985)

Załóżmy, że chcemy poznać dzień tygodnia 18 września 1985 roku. Zaczynamy od dnia kotwicy stulecia, czyli środy. Do tego dodaj $a$ , $b$ i $c$ powyżej:

$a$ to podłoga $85 / 12$ , czyli 7.
$b$ to $85 mod 12$ , czyli $1$ .
$c$ to podłoga $b / 4$ , czyli 0.

Daje to $a + b + c = 8$ . Licząc 8 dni od środy, dochodzimy do czwartku, który jest dniem zagłady w 1985 r. (Korzystając z liczb: w arytmetyce modulo 7 8 jest równe 1. Ponieważ dniem zakotwiczenia stulecia jest środa (indeks 3), a 3 + 1 = 4 , dzień zagłady w 1985 roku był w czwartek (indeks 4). Teraz porównujemy 18 września z pobliskim dniem zagłady, 5 września. Widzimy, że 18-ty jest 13 po dniu zagłady, tj. jeden dzień mniej niż dwa tygodnie. Dlatego 18-go wypadała w środę (dzień poprzedzający czwartek). (Korzystając z liczb: w arytmetyce modulo 7 13 jest zgodne z 6 lub, mówiąc bardziej zwięźle, -1. W ten sposób odejmujemy jeden od dnia zagłady, czwartku, aby stwierdzić, że 18 września 1985 r. Wypadł w środę).

Przykład 2 (inne stulecia)

Załóżmy, że chcemy znaleźć dzień tygodnia, w którym w Fort Sumter wybuchła wojna secesyjna , czyli 12 kwietnia 1861 r. Dzień kotwicy stulecia przypadał 99 dni po czwartku, czyli innymi słowy po piątku (liczony jako $(18 + 1) \times 5 + ⌊ 18 / 4 ⌋$ ; lub po prostu spójrz na powyższy wykres, który zawiera listę dni zakotwiczenia stulecia). Cyfry 61 oznaczały przesunięcie o sześć dni, więc dniem zagłady był czwartek. Dlatego 4 kwietnia był czwartek, więc 12 kwietnia, osiem dni później, był piątek.

Zobacz też

Data porządkowa
Computus – algorytm Gaussa do obliczania daty Wielkanocy
Kongruencja Zellera - algorytm (1882) do obliczania dnia tygodnia dla dowolnej daty kalendarza juliańskiego lub gregoriańskiego.
Kalkulacja mentalna

Linki zewnętrzne