Dwoistość Pontriagina

2 -adyczne liczby całkowite z wybranymi odpowiednimi znakami w ich podwójnej grupie Pontryagin

W matematyce dualizm Pontryagina to dualizm między lokalnie zwartymi grupami abelowymi , który pozwala uogólnić transformatę Fouriera na wszystkie takie grupy, które obejmują grupę kołową (multiplikatywną grupę liczb zespolonych o module jeden), skończone grupy abelowe (z topologią dyskretną ) , oraz grupa addytywna liczb całkowitych (również z topologią dyskretną), liczby rzeczywiste i każda skończenie wymiarowa przestrzeń wektorowa nad liczbami rzeczywistymi lub a p -adyczne pole .

Podwójny Pontryagina lokalnie zwartej grupy abelowej jest lokalnie zwartą abelową grupą topologiczną utworzoną przez ciągłe homomorfizmy grupowe od grupy do grupy kołowej z operacją punktowego mnożenia i topologią jednostajnej zbieżności na zbiorach zwartych. Twierdzenie Pontryagina o dwoistości ustanawia dualizm Pontryagina, stwierdzając, że każda lokalnie zwarta grupa abelowa jest naturalnie izomorficzna ze swoim bidualem (dualizmem dualności). Twierdzenie o inwersji Fouriera jest szczególnym przypadkiem tego twierdzenia.

Przedmiot został nazwany na cześć Lwa Pontryagina , który podczas swoich wczesnych prac matematycznych w 1934 r. położył podwaliny pod teorię lokalnie zwartych grup abelowych i ich dwoistości. Pontryagin w swoich terapiach opierał się na tym, że grupy są policzalne jako drugie oraz zwarte lub dyskretne. Zostało to ulepszone, aby uwzględnić ogólne lokalnie zwarte grupy abelowe przez Egberta van Kampena w 1935 r. i André Weila w 1940 r.

Wstęp

Dualizm Pontryagina umieszcza w ujednoliconym kontekście szereg obserwacji dotyczących funkcji na prostej rzeczywistej lub na skończonych grupach abelowych:

• Odpowiednio regularne funkcje okresowe o wartościach zespolonych na prostej rzeczywistej mają szereg Fouriera i funkcje te można odzyskać z ich szeregów Fouriera;
• Odpowiednio regularne funkcje o wartościach zespolonych na linii rzeczywistej mają transformaty Fouriera, które są również funkcjami na linii rzeczywistej i, podobnie jak w przypadku funkcji okresowych, funkcje te można odzyskać z ich transformat Fouriera; I
• Funkcje o wartościach zespolonych na skończonej grupie abelowej mają dyskretne transformaty Fouriera , które są funkcjami na grupie podwójnej , która jest (niekanonicznie) grupą izomorficzną. Co więcej, dowolną funkcję skończonej grupy abelowej można odzyskać z jej dyskretnej transformaty Fouriera.

Teoria wprowadzona przez Leva Pontryagina i połączona z miarą Haara wprowadzoną przez Johna von Neumanna , André Weila i innych opiera się na teorii grupy podwójnej lokalnie zwartej grupy abelowej.

Jest to analogiczne do podwójnej przestrzeni wektorowej przestrzeni wektorowej: skończenie wymiarowa przestrzeń wektorowa V i jej podwójna przestrzeń wektorowa V * nie są naturalnie izomorficzne, ale algebra endomorfizmu (algebra macierzy) jednego jest izomorficzna z przeciwieństwem endomorfizmu algebra drugiego: ${\ Displaystyle {\ tekst {Koniec}} (V) \ cong {{\ tekst {Koniec}} (V ^ {*})} ^ { \text{op}},}$ poprzez transpozycję. Podobnie grupa ${\ Displaystyle {\ tekst {koniec}} (G) \ cong {\ tekst {koniec}} ({\ widehat {G}}) ^ {\ tekst {op}}}$ grupa nie generalnie izomorficzne, ale ich pierścienie endomorfizmu są do siebie przeciwne: ${$$}}$ . Mówiąc bardziej kategorycznie, nie jest to tylko izomorfizm algebr endomorfizmu, ale kontrawariantna równoważność kategorii – zob. kategoryczne rozważania .

Definicja

Dalsze informacje: Lokalnie zwarta grupa abelowa

Grupa topologiczna jest grupą lokalnie zwartą, jeśli podstawowa przestrzeń topologiczna jest lokalnie zwarta i Hausdorffa ; grupa topologiczna jest abelowa , jeśli podstawowa grupa jest abelowa . Przykłady lokalnie zwartych grup abelowych obejmują skończone grupy abelowe, liczby całkowite (obie dla topologii dyskretnej , która jest również indukowana przez zwykłą metrykę), liczby rzeczywiste, grupę kołową T (obie ze zwykłą topologią metryczną), a także p -liczby adyczne (z ich typową topologią p -adyczną).

W przypadku lokalnie zwartej grupy abelowej $styl wyświetlania T}$$dualność$ Pontryagina to $sol$ ciągłych homomorfizmów grupowych od grupy kołowej $displaystyle$$G$ . To jest,

$${\ Displaystyle {\ widehat {G}}: = \ operatorname {Hom} (G, T).}$$

$}$ Pontryagina jest zwykle wyposażony w topologię określoną przez jednolitą zbieżność na zbiorach zwartych (to znaczy topologię indukowaną topologią zwarto-otwartą w przestrzeni wszystkich funkcji ciągłych z sol ^ {\ displaystyle {\ widehat {G} ${\ displaystyle G}$ do ${\ displaystyle T}$ ).

Na przykład,

$${\ Displaystyle {\ widehat {\ mathbb {Z} / n \ mathbb {Z}}} = \ mathbb {Z} / n \ mathbb {Z}, \ {\ widehat {\ mathbb {Z}}} = T, \ {\widehat {\mathbb {R} }}=\mathbb {R} ,\ {\widehat {T}}=\mathbb {Z} .}$$

Twierdzenie Pontryagina o dualności

Twierdzenie - Istnieje kanoniczny izomorfizm $podwójnym$$dowolną$ lokalnie zwartą i

Kanoniczny oznacza, że ​​istnieje naturalnie zdefiniowana mapa ${\ displaystyle \ operatorname {ev} _ {G} \ dwukropek G \ do {\ widehat {\ widehat {G}}}}$ ; $powinna$ ważniejsze, mapa być funkcjonalna . Izomorfizm kanoniczny $}$ zdefiniowany w następujący sposób: $\ displaystyle \ operatorname {ev} _ {G$

$${\ Displaystyle \ operatorname {ev} _ {G} (x) (\ chi) = \ chi (x) \ in \ mathbb {T}.}$$

To jest,

$${\ Displaystyle \ nazwa operatora {ev} _ {G} (x): (\ chi \ mapsto \ chi (x)).}$$

Innymi słowy, każdy element grupy $jest$ ze znakiem oceny w liczbie podwójnej. Jest to silnie analogiczne do $a$ izomorfizmu między skończenie wymiarową przestrzenią wektorową jej $podwójną$ i wspomnieć, że dowolna $\displaystyle V}$ { jest grupą abelową . Jeśli ${\ displaystyle G}$$jest$ grupą abelową, to kanoniczny Doprecyzowanie tego stwierdzenia (w ogóle) wymaga przemyślenia dualizacji nie tylko na grupach, ale także na mapach pomiędzy grupami, aby potraktować dualizm jako funktor i udowodnić, że funktor tożsamości i funktor dualizacji nie są w sposób naturalny równoważne. Również twierdzenie o dwoistości implikuje, że dla dowolnej grupy (niekoniecznie skończonej) funktor dualizacji jest funktorem dokładnym .

Dualizm Pontryagina i transformata Fouriera

Miara Haara

Główny artykuł: miara Haara

Jednym z najbardziej niezwykłych faktów dotyczących grupy lokalnie zwartej $to$ , że zawiera ona zasadniczo unikalną miarę naturalną , miarę Haara , która pozwala konsekwentnie mierzyć „rozmiar” wystarczająco regularnych podzbiorów grupy sol ${\ displaystyle$ . „Wystarczająco regularny podzbiór” oznacza tutaj zbiór borelowski ; czyli element σ-algebry generowanej przez zbiory zwarte . Dokładniej, właściwa miara Haara na grupie lokalnie zwartej $jest$ przeliczalnie addytywną miarą μ zdefiniowaną na zbiorach borelowskich, $displaystyle G}$ jest niezmienna w prawo w μ ( tym ) = μ ( ZA ) sensie, że dla $x}$${\ sol {\$$displaystyle$ element i $podzbiór$ borelowy $displaystyle G}$ a także spełnia pewne warunki regularności (opisane szczegółowo w artykule o miarze Haara ). Z wyjątkiem dodatnich współczynników skalujących, miara Haara $jest$ .

Miara Haara $wartościach$ nam zdefiniować pojęcie całki dla (o zespolonych ) funkcji borelowych zdefiniowanych w grupie. W szczególności można rozważyć różne przestrzenie L ^p powiązane z miarą Haara μ. Konkretnie,

$${\ Displaystyle {\ mathcal {L}} _ {\ mu } ^ {p} (G) = \ lewo \ {(f: G \ do \ mathbb {C}) \ {\ Duży |} \ \ int _ { G}|f(x)|^{p}\ d\mu (x)<\infty \right\}.}$$

Należy zauważyć, że ponieważ dowolne dwie miary Haara na $\$ równe aż do współczynnika skalowania, ta –przestrzeń jest niezależna od wyboru miary Haara i dlatego być może mogłaby być $displaystyle L ^ {p}}$ zapisane jako ${\ Displaystyle L ^ {p} (G)}$ . Jednak norma w tej przestrzeni zależy od wyboru miary Haara, więc jeśli ktoś chce rozmawiać o izometrii, ważne jest, aby śledzić używaną $miarę$

Transformata Fouriera i wzór na inwersję Fouriera dla funkcji L ¹

Grupa podwójna lokalnie zwartej grupy abelowej jest używana jako przestrzeń bazowa dla abstrakcyjnej wersji transformaty Fouriera . Jeśli , to transformata Fouriera jest funkcją na fa $in L ^ {1} ($$}$$\$${\ widehat {G}}}$ zdefiniowany przez

$${\ Displaystyle {\ widehat {f}} (\ chi) = \ int _ {G} f (x) {\ overline {\chi (x)}}\ d\mu (x),}$$

gdzie całka jest zależna od miary Haara , ${\ displaystyle \ mu}$ na ${\ displaystyle G}$ . Jest to również oznaczone ${\ Displaystyle ({\ mathcal {F}} f) (\ chi)}$ . Należy zauważyć, że transformata Fouriera zależy od wyboru miary Haara. $,$ że transformata Fouriera funkcji $G$ jest ograniczoną funkcją ciągłą ${\ displaystyle {\ widehat {G}}}$ , który znika w nieskończoności .

Wzór na inwersję Fouriera dla $-$ ^ -Funkcje Dla każdej ${1}$ Haara na istnieje unikalna miara Haara na $displaystyle$${$ } ${\ displaystyle {\ widehat {G}}}$ tak, że ilekroć ${\ displaystyle f \ in L ^ {1} (G)}$ i ${\ Displaystyle {\ widehat {f}} \ w L ^ {1} \ lewo ({\ widehat {G}} \ prawo)}$ , mamy

$${\ Displaystyle f (x) = \ int _ {\ widehat {G}} {\ widehat {f} }(\chi )\chi (x)\ d\nu (\chi )\qquad \mu {\text{-prawie wszędzie}}}$$

Jeśli $jest$$ciągła,$ tożsamość ta obowiązuje dla .

Odwrotna transformata Fouriera funkcji całkowalnej jest dana wzorem ${\ displaystyle {\ widehat {G}}}$

$${\ Displaystyle {\ sprawdź {g}} (x) = \ int _ {\ widehat {G}} g (\ chi )\chi (x)\ d\nu (\chi ),}$$

$gdzie$ całka jest zależna od $podwójnej$ grupie . Miara we wzorze inwersji $widehat {G}$ , nazywana jest miarą podwójną do i może być oznaczona jako miara $}$$} \ Displaystyle {\ widehat {\ mu}}}$${\$ .

Różne transformaty Fouriera można sklasyfikować pod względem ich dziedziny i domeny transformacji (grupy i grupy podwójnej) w następujący sposób (zauważ, że jest to grupa okrąg ): ${\ displaystyle \ mathbb {T}}$

Przekształcać	Oryginalna domena, ${\ displaystyle G}$	Przekształć domenę, ${\ displaystyle {\ kapelusz {G}}}$	Zmierz, ${\ displaystyle \ mu}$
Transformata Fouriera	${\ displaystyle \ mathbb {R}}$	${\ displaystyle \ mathbb {R}}$	${\ displaystyle {\ tekst {stała}} \ razy {\ tekst {miara Lebesgue'a}}}$
Szereg Fouriera	${\ displaystyle \ mathbb {T}}$	${\ displaystyle \ mathbb {Z}}$	${\ displaystyle {\ tekst {stała}} \ razy {\ tekst {miara Lebesgue'a}}}$
Dyskretna transformata Fouriera (DTFT)	${\ displaystyle \ mathbb {Z}}$	${\ displaystyle \ mathbb {T}}$	${\ displaystyle {\ tekst {stała}} \ razy {\ tekst {miara licząca}}}$
Dyskretna transformata Fouriera (DFT)	${\ displaystyle \ mathbb {Z} _ {n}}$	${\ displaystyle \ mathbb {Z} _ {n}}$	${\ displaystyle {\ tekst {stała}} \ razy {\ tekst {miara licząca}}}$

$R} ^ {$ na przykład, że możemy pomyśleć o tym, ${$ n $} mathbb {R} ^{n}}$ przez parowanie ${\ Displaystyle (\ mathbf {v}, \ mathbf {w}) \ mapsto e ^ {i \ mathbf {v} \ cdot \ mathbf {w}}.} Jeśli μ {\ displaystyle$ \ $}$${\ Displaystyle {\ Widehat {\ mu}} = (2 \ pi) ^ {- n} \ mu}$ przestrzeni euklidesowej, otrzymujemy zwykłą transformatę Fouriera , $a$ miara podwójna potrzebna do wzoru na inwersję Fouriera to . Jeśli chcemy uzyskać wzór na inwersję Fouriera z tą samą miarą po obu stronach (to znaczy, ponieważ możemy pomyśleć o ${\ displaystyle \ mathbb {R} ^ {n}}$$),$$musimy$ możemy poprosić , aby była równa użyć

$${\ Displaystyle {\ początek {wyrównane} \ mu i = (2 \ pi) ^ {- {\ Frac { n}} {\text{miara Lebesgue’a}}\end{aligned}}}$$

Jeśli jednak zmienimy sposób, w jaki identyfikujemy się $z$ grupą, używając parowania

$${\ Displaystyle (\ mathbf {v}, \ mathbf {w}) \ mapsto e ^ {2 \ pi ja \ mathbf {v} \ cdot \ mathbf {w } },}$$

$wówczas miara$ jest własnej podwójnej mierze. Konwencja ta minimalizuje liczbę czynników $euklidesowej$ które pojawiają się w różnych miejscach podczas obliczania transformat Fouriera lub odwrotnych transformat Fouriera w przestrzeni (W efekcie ogranicza to tylko do wykładnika, a nie jako czynnik wstępny poza znakiem $displaystyle \ mathbb {R} ^{n}}$ ). Należy zauważyć, że wybór sposobu identyfikacji jest $\$$parowania$ „funkcja samopodwójna”, która jest funkcją równą własnej transformacie Fouriera: przy użyciu klasycznego ${\ Displaystyle (\ mathbf {v}, \ mathbf {w}) \ mapsto e ^ {i \ mathbf {v} \ cdot \ mathbf {w}}}$ funkcja ${\ Displaystyle e ^ {- {\ Frac {1} {2}} x ^ {2}}}$ jest samodualny. Ale używając parowania, które utrzymuje współczynnik wstępny jako jedność, $pi ja \ mathbf {v} \ cdot \ mathbf {w}}}$${\ Displaystyle (\ mathbf {v}, \ mathbf {w}) \ mapsto e ^ {2 \$ zamiast tego sprawia, ${\ displaystyle e ^ {- \ pi x ^ {2}}}$ Ta druga definicja transformaty Fouriera ma tę zaletę, że odwzorowuje tożsamość multiplikatywną na tożsamość splotu, co jest przydatne jako ${\ displaystyle L ^ {1}}$ jest algebrą splotu. Zobacz następną sekcję dotyczącą algebry grupowej . Ponadto ta forma jest również koniecznie $przestrzeniach$ . Zobacz poniżej Plancherela i L2 o ^inwersji Fouriera .

Algebra grupowa

Główny artykuł: Algebra grupowa grupy lokalnie zwartej

Przestrzeń funkcji całkowalnych na lokalnie zwartej grupie abelowej $mnożenie$ algebrą , gdzie jest splotem: splot dwóch funkcji całkowalnych $zdefiniowany$ jest jako ${\ displaystyle G}$

$${\ Displaystyle (f * g) (x) = \ int _ {G} f (xy) g (y) \ d \ mu (y).}$$

Twierdzenie - Przestrzeń Banacha $.$ i przemienną

$ta$ nazywana jest algebrą grupową . Zgodnie z $Tonelliego$ splot jest submultiplikatywny w $normy$ , co algebrę Banacha Algebra Banacha $multiplikatywny$ element tożsamości wtedy i ${\ displaystyle G}$ to grupa dyskretna, a mianowicie funkcja, która wynosi 1 w tożsamości i zero gdzie indziej. Ogólnie jednak ma przybliżoną tożsamość $,$ siecią (lub uogólnioną sekwencją skierowanym ${\ displaystyle I}$ tak, że ${\ Displaystyle f * e_ {i} \ do f.}$

Transformata Fouriera prowadzi splot do mnożenia, tj. jest homomorfizmem abelowych algebr Banacha. ${\ displaystyle L ^ {1} (G) \ do C_ {0} \ lewo ({\ widehat {G}}\right)}$ (o normie ≤ 1):

$${\ Displaystyle {\ mathcal {F}} (f * g) (\ chi) = {\ mathcal {F}} (f) (\ chi) \ cdot {\ mathcal {F}} (g) (\ chi) .}$$

W szczególności każdemu znakowi grupowemu odpowiada unikalny multiplikatywny funkcjonał liniowy w algebrze grupy zdefiniowanej przez sol {\ displaystyle $}$

$${\ Displaystyle f \ mapsto {\ widehat {f}} (\ chi).}$$

Ważną właściwością algebry grup jest to, że wyczerpują one zbiór nietrywialnych (to znaczy nie identycznych zerowych) multiplikatywnych funkcjonałów liniowych w algebrze grupowej; patrz sekcja 34 ( Loomis 1953 ). Oznacza to, że transformata Fouriera jest szczególnym przypadkiem transformaty Gelfanda .

Twierdzenia Plancherela i L ^{2 o inwersji Fouriera}

Jak już powiedzieliśmy, grupa dualna lokalnie zwartej grupy abelowej jest lokalnie zwartą grupą abelową samą w sobie i dlatego ma miarę Haara, a dokładniej całą rodzinę miar Haara związanych ze skalą.

Twierdzenie - Wybierz miarę Haara $niech$ i będzie ${\ widehat {G}}},$ miarą na $\$$displaystyle$ zdefiniowano powyżej . Jeśli ${\ displaystyle f: G \ do \ mathbb {C}}$ jest ciągły ze zwartym wsparciem, to ${\ Displaystyle {\ widehat {f}} \ w L ^ {2} \ lewo ({\ widehat {G}} \ prawo)}$ i

$${\ Displaystyle \ int _ {G} | f (x) | ^ {2} \ d \ mu (x) = \ int _ {\ widehat {G}} \ lewo | {\ widehat {f}} (\ chi )\right|^{2}\ d\nu (\chi ).}$$

$^ {2}}$ szczególności transformata Fouriera jest $displaystyle$ funkcji ciągłych o wartościach zespolonych zwartego wsparcia do $L$$}}$ na (przy użyciu -normy w odniesieniu do funkcji na ${\$$displaystyle {\$${$ i $\ widehat {G}}$ w odniesieniu do funkcji na $displaystyle$${$ }

Ponieważ funkcje ciągłe o wartościach zespolonych zwartego wsparcia $,$$unikalne$ istnieje rozszerzenie transformaty Fouriera z tej przestrzeni na operator unitarny

$${\ Displaystyle {\ mathcal {F}}: L _ {\ mu } ^ {2} (G) \ do L _ {\ nu} ^ {2} \ lewo ({\ widehat {G}} \ prawo).}$$

i mamy formułę

$${\ Displaystyle \ forall f \ in L ^ {2} (G): \ quad \ int _ {G} | f (x) | ^ {2} \ d \ mu (x) = \ int _ {\ widehat { G}}\left|{\widehat {f}}(\chi )\right|^{2}\ d\nu (\chi ).}$$

$^$$,$ przypadku niezwartych lokalnie zwartych grup przestrzeń nie zawiera $L$ , więc transformata Fouriera ogólnych $.$ „ $”$ jest „nie” dana przez jakikolwiek wzór całkowania (lub tak naprawdę dowolny wyraźny wzór) Aby zdefiniować Transformata Fouriera wymaga zastosowania jakiejś sztuczki technicznej, takiej jak rozpoczęcie od gęstej podprzestrzeni, takiej jak funkcje ciągłe ze zwartym wsparciem, a następnie rozszerzenie izometrii o ciągłość na całą przestrzeń $.$ To jednolite rozszerzenie transformaty Fouriera jest tym, co rozumiemy przez transformatę Fouriera na przestrzeni kwadratowych funkcji całkowalnych.

Grupa podwójna ma również samą odwrotną transformatę Fouriera; $transformaty$ jako odwrotność (lub sprzężenie, ponieważ jest unitarna) Fouriera. To jest treść poniższego $na inwersję$ .

Twierdzenie — Spójną transformatą Fouriera ograniczoną do funkcji ciągłych zwartego nośnika jest odwrotna transformata Fouriera

$${\ Displaystyle L _ {\ nu} ^ {2} \ lewo ({\ widehat {G}} \ prawo) \ do L _ {\ mu} ^ {2} (G)}$$

gdzie $\ displaystyle \ mu}$ podwójną miarą ${$ .

W przypadku, gdy grupa podwójna ${\ displaystyle G =$ naturalnie izomorficzna z grupą liczb całkowitych, $\$$}$${T}$ , a transformata Fouriera specjalizuje się w obliczaniu współczynników szeregu Fouriera funkcji okresowych.

Jeśli $skończoną$ , odzyskujemy dyskretną transformatę Fouriera . Należy pamiętać, że ten przypadek jest bardzo łatwy do udowodnienia bezpośrednio.

Zagęszczenie Bohra i prawie okresowość

Jednym z ważnych zastosowań dualności Pontryagina jest następująca charakterystyka zwartych abelowych grup topologicznych:

Twierdzenie - Lokalnie zwarta $grupa$ abelowa jest wtedy i tylko wtedy, gdy $podwójna$ jest . $zwarty$ , jest dyskretny wtedy i tylko wtedy, $jest$ .

Że $​​sol$ oznacza, że ​​jest $}$$displaystyle {\ widehat {G}$ lub że dyskretność oznacza, że $\$$,$ jest elementarną konsekwencją definicji topologii zwarto-otwartej nie wymaga dualności Pontryagina Aby udowodnić coś odwrotnego, używa się dualności Pontryagina.

Zagęszczenie Bohra $zwarta$ zdefiniowane dla dowolnej grupy topologicznej $,$ niezależnie od tego, czy jest lokalnie czy abelowa. Jednym z zastosowań dualności Pontryagina między zwartymi grupami abelowymi i dyskretnymi grupami abelowymi jest scharakteryzowanie zagęszczenia Bohra dowolnej abelowej, lokalnie zwartej grupy topologicznej. Zagęszczenie Bohra to H. $B (G)}$${\ displaystyle G}$ sol , gdzie H ma strukturę grupową $ale$ biorąc pod $uwagę$ topologię Od mapy włączenia

$${\ Displaystyle \ jota: H \ do {\ widehat {G}}}$$

jest ciągły i jest homomorfizmem, morfizmem podwójnym

$${\ Displaystyle G \ sim {\ widehat {\ widehat {G}}} \ do {\ widehat {H}}}$$

jest morfizmem w grupę zwartą, co do którego łatwo można wykazać, że spełnia wymaganą uniwersalną właściwość .

Zobacz także: funkcja prawie okresowa

Kategoryczne rozważania

Dualizm Pontryagina można również z korzyścią rozpatrywać w sposób funkcjonalny . Poniżej LCA jest kategorią lokalnie zwartych grup abelowych i ciągłych homomorfizmów grupowych. Konstrukcja dwugrupowa $jest$ funktorem kontrawariantnym → LCA , reprezentowanym (w sensie reprezentowalnych funktorów ) przez grupę kołową jako $}}$ \ mathbb { T $sol$ W szczególności podwójny podwójny funktor ${\ displaystyle G \ do {\$ jest kowariantem . Kategoryczne sformułowanie dualności Pontryagina stwierdza następnie, że naturalna transformacja między funktorem tożsamości na LCA a podwójnym funktorem dualnym jest izomorfizmem. Rozwijając pojęcie transformacji naturalnej, oznacza to, że mapy ${\ Displaystyle G \ do \ operatorname {Hom} (\ operatorname {Hom} (G, T), T)}$ są izomorfizmami dla dowolnej lokalnie zwartej grupy abelowej $G}$${\$$displaystyle$ , a te izomorfizmy są funkcyjne . Izomorfizm ten jest analogiczny do podwójnego dualizmu skończenie wymiarowych przestrzeni wektorowych (przypadek szczególny dla rzeczywistych i zespolonych przestrzeni wektorowych).

Bezpośrednią konsekwencją tego sformułowania jest inne powszechne kategoryczne sformułowanie dualności Pontryagina: podwójny funktor grupowy jest równoważnością kategorii od LCA do LCA ^op .

Dwoistość zamienia podkategorie grup dyskretnych i grup zwartych . Jeśli jest $pierścieniem$ i jest lewym modułem , podwójna grupa $}$ prawym $R$$\$${\ displaystyle R}$ – moduł; w ten sposób możemy również zobaczyć, że dyskretny lewy $moduły$ będą podwójne Pontryagina do zwartego prawego $_$ . Pierścień Endomorfizmów w LCA jest zmieniany przez dualizm w przeciwny pierścień ( $G)}$ ( (zmień mnożenie na inny porządek). Na przykład jeśli jest $nieskończoną$$pierwsza$ grupą dyskretną, jest to grupa okręgowa: ${\ displaystyle {\ tekst {koniec}} (G) = \ mathbb {Z}},$ więc dotyczy to również tego ostatniego.

Uogólnienia

Uogólnienia dualności Pontryagina są konstruowane w dwóch głównych kierunkach: dla przemiennych grup topologicznych , które nie są lokalnie zwarte , oraz dla nieprzemiennych grup topologicznych. Teorie w tych dwóch przypadkach są bardzo różne.

Dualizmy dla przemiennych grup topologicznych

Kiedy jest abelową grupą topologiczną $G$ , grupa z topologią zwarto-otwartą jest abelową grupą topologiczną Hausdorffa i naturalnym odwzorowaniem z $} do$$\$$}$$.$ podwójnego dualizmu sens Jeśli to odwzorowanie jest izomorfizmem, mówi się, że spełnia dualizm $displaystyle$ (lub że $G}$ jest grupą refleksyjną lub grupą refleksyjną ). Zostało to rozszerzone w wielu kierunkach poza przypadek, w którym $lokalnie$ zwarty.

W szczególności Samuel Kaplan wykazał w latach 1948 i 1950, że iloczyny dowolne i przeliczalne odwrotne granice lokalnie zwartych (Hausdorffa) grup abelowych spełniają dualizm Pontryagina. Należy zauważyć, że nieskończony iloczyn lokalnie zwartych, niezwartych przestrzeni nie jest lokalnie zwarty.

Później, w 1975 roku, Rangachari Venkataraman wykazał między innymi, że każda otwarta podgrupa abelowej grupy topologicznej, która sama spełnia dualizm Pontryagina, sama spełnia dualizm Pontryagina.

Niedawno Sergio Ardanza-Trevijano i María Jesús Chasco rozszerzyli wspomniane powyżej wyniki Kaplana. Pokazali, że bezpośrednie i odwrotne granice ciągów grup abelowych spełniające dualizm Pontryagina spełniają również dualizm Pontryagina $niekoniecznie$ jeśli grupy są metryzowalne lub -przestrzenie, lokalnie zwarte, pod warunkiem, że spełnione zostaną pewne dodatkowe warunki przez sekwencje.

Istnieje jednak zasadniczy aspekt, który się zmienia, jeśli chcemy rozważyć dualizm Pontryagina poza przypadkiem lokalnie zwartym. Elena Martín-Peinador udowodniła w 1995 roku $,$ że jeśli jest abelową grupą topologiczną Hausdorffa, która spełnia dualizm Pontryagina i naturalne parowanie

$${\ Displaystyle {\ początek {przypadków} G \ razy {\ widehat {G}} \ do \ mathbb {T} \\ (x, \ chi )\mapsto \chi (x)\end{cases}}}$$

jest (łącznie) ciągły, to $zwarty$ . W rezultacie wszystkie nielokalnie zwarte przykłady dualności Pontryagina to grupy, w których parowanie nie jest (łącznie) ${\ displaystyle G \ razy {\ widehat {G}} \ do \ mathbb {T}}$ ciągły.

topologicznych jest wyposażenie grupy podwójnej $.$ nieco inną topologię, a mianowicie topologię jednolitej zbieżności na całkowicie zbiorach Grupy spełniające tożsamość przy tym założeniu nazywane są grupami stereotypowymi ${\ displaystyle G \ cong {\ widehat {\ widehat {G}}}}$ . Klasa ta jest również bardzo szeroka (i zawiera lokalnie zwarte grupy abelowe), ale jest węższa niż klasa grup refleksyjnych.

Dualizm Pontryagina dla topologicznych przestrzeni wektorowych

W 1952 roku Marianne F. Smith zauważyła, że ​​przestrzenie Banacha i przestrzenie zwrotne , traktowane jako grupy topologiczne (z addytywną operacją grupową), spełniają dualizm Pontryagina. Później BS Brudovskiĭ, William C. Waterhouse i K. Brauner wykazali, że wynik ten można rozszerzyć na klasę wszystkich quasi-kompletnych przestrzeni beczkowych (w szczególności na wszystkie przestrzenie Frécheta ). W latach 90. Siergiej Akbarow podał opis klasy topologicznych przestrzeni wektorowych, które spełniają silniejszą właściwość niż klasyczna zwrotność Pontriagina, a mianowicie tożsamość

$${\ Displaystyle (X ^ {\ gwiazda}) ^ {\ gwiazda} \ cong X}$$

gdzie oznacza przestrzeń wszystkich liniowych funkcjonałów ciągłych, $\ gwiazda}}$ topologię jednolitej zbieżności na całkowicie $displaystyle X ^$ ograniczone zbiory w (i ${\ gwiazda}) ^ {\ gwiazda}}$$)$${\ displaystyle X ^ {\ gwiazda}$ oznaczają podwójną wartość w tym samym sensie). Przestrzenie tej klasy nazywane są przestrzeniami stereotypowymi , a odpowiadająca im teoria znalazła szereg zastosowań w analizie funkcjonalnej i geometrii, w tym uogólnienie dualności Pontryagina dla nieprzeprzemiennych grup topologicznych.

Dualizmy dla nieprzemiennych grup topologicznych

${\ displaystyle G}$ nieprzeprzemiennych grup lokalnie zwartych klasyczna konstrukcja $Pontryagina przestaje działać z różnych powodów,$$G$ nie zawsze oddzielają punkty i nieredukowalne reprezentacje nie zawsze są jednowymiarowe. Jednocześnie nie jest jasne, jak wprowadzić mnożenie na zbiorze nieredukowalnych reprezentacji unitarnych ${\ displaystyle G}$ , i nawet nie jest jasne, czy ten zestaw jest dobrym wyborem do roli podwójnego $dla$ . Zatem problem konstruowania dualności w tej sytuacji wymaga całkowitego przemyślenia.

Dotychczasowe teorie dzielą się na dwie główne grupy: teorie, w których przedmiot dualny ma tę samą naturę co przedmiot źródłowy (jak w samym dualności Pontryagina) oraz teorie, w których przedmiot źródłowy i jego dualność różnią się od siebie tak radykalnie że nie da się ich zaliczyć do obiektów jednej klasy.

Teorie drugiego typu były historycznie pierwszymi: wkrótce po pracy Pontryagina Tadao Tannaka (1938) i Mark Kerin (1949) skonstruowali teorię dualności dla dowolnych zwartych grup, znaną obecnie jako dualizm Tannaki – Kreina . $teorii$ podwójny obiekt dla grupy nie $kategorią$ ale jej reprezentacji

Dualizm dla grup skończonych.

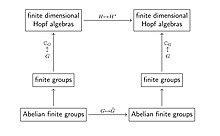
Teorie pierwszego typu pojawiły się później, a kluczowym dla nich przykładem była teoria dualności grup skończonych. W tej teorii kategoria grup skończonych jest osadzona w operacji ${C} _ {$ algebry grupowej do $\ mapsto \ mathbb$ ponad ) do kategorii $skończenie wymiarowych$ algebr Hopfa , tak że funktor dualności Pontryagina $przestrzeni$ w operację polegającą na wzięciu podwójnej wektora (która $w$ kategorii skończenie wymiarowe algebry Hopfa).

W 1973 roku Leonid I. Vainerman, George I. Kac, Michel Enock i Jean-Marie Schwartz zbudowali ogólną teorię tego typu dla wszystkich grup lokalnie zwartych. Od lat 80. XX w. badania w tym obszarze zostały wznowione po odkryciu grup kwantowych , do których zaczęto aktywnie przenosić skonstruowane teorie. Teorie te formułowane są w języku C*-algebr , czyli algebr Von Neumanna , a jednym z jej wariantów jest najnowsza teoria lokalnie zwartych grup kwantowych .

Jedną z wad tych ogólnych teorii jest jednak to, że w nich obiekty uogólniające pojęcie grupy nie są algebrami Hopfa w zwykłym algebraicznym sensie. Brak ten można skorygować (dla niektórych klas grup) w ramach teorii dualności budowanych w oparciu o pojęcie obwiedni algebry topologicznej.

Zobacz też

• Twierdzenie Petera-Weyla
• Dualizm Cartiera
• Przestrzeń stereotypowa

Notatki

•   Akbarow, SS (2003). „Dwoistość Pontryagina w teorii topologicznych przestrzeni wektorowych i algebrze topologicznej” . Journal of Mathematical Sciences . 113 (2): 179–349. doi : 10.1023/A:1020929201133 . S2CID 115297067 .
• Akbarow, Siergiej S.; Shavgulidze, Evgeniy T. (2003). „O dwóch klasach przestrzeni refleksyjnych w sensie Pontryagina” . Matematicheskii Sbornik . 194 (10): 3–26.
•   Akbarow, Siergiej S. (2009). „Funkcje holomorficzne typu wykładniczego i dualności dla grup Steina z algebraicznie połączonym składnikiem tożsamości”. Journal of Mathematical Sciences . 162 (4): 459–586. arXiv : 0806.3205 . doi : 10.1007/s10958-009-9646-1 . S2CID 115153766 .
•    Akbarow, Siergiej S. (2017a). „Ciągłe i gładkie obwiednie algebr topologicznych. Część 1”. Journal of Mathematical Sciences . 227 (5): 531–668. arXiv : 1303.2424 . doi : 10.1007/s10958-017-3599-6 . MR 3790317 . S2CID 126018582 .
•    Akbarow, Siergiej S. (2017b). „Ciągłe i gładkie obwiednie algebr topologicznych. Część 2”. Journal of Mathematical Sciences . 227 (6): 669–789. arXiv : 1303.2424 . doi : 10.1007/s10958-017-3600-4 . MR 3796205 . S2CID 128246373 .
• Brauner, Kalman (1973). „Dualy przestrzeni Frécheta i uogólnienie twierdzenia Banacha – Dieudonnégo”. Duke Mathematical Journal . 40 (4): 845–855. doi : 10.1215/S0012-7094-73-04078-7 .
• Brudowski, BS (1967). „O k- i c-zwrotności lokalnie wypukłych przestrzeni wektorowych”. Litewski Dziennik Matematyczny . 7 (1): 17–21.
•   Dixmier, Jacques (1969). Les C*-algèbres et leurs Reprezentacje . Gauthier-Villars. ISBN 978-2-87647-013-2 .
•    Enock, Michel; Schwartz, Jean-Marie (1992). Algebry Kaca i dualizm grup lokalnie zwartych . Z przedmową Alaina Connesa. Z postem Adriana Ocneanu. Berlin: Springer-Verlag. doi : 10.1007/978-3-662-02813-1 . ISBN 978-3-540-54745-7 . MR 1215933 .
•    Hewitt, Edwin; Ross, Kenneth A. (1963). Abstrakcyjna analiza harmoniczna. Tom. I: Struktura grup topologicznych. Teoria integracji, reprezentacje grupowe . Die Grundlehren der mathematischen Wissenschaften. Tom. 115. Berlin-Göttingen-Heidelberg: Springer-Verlag. ISBN 978-0-387-94190-5 . MR 0156915 .
•    Hewitt, Edwin; Ross, Kenneth A. (1970). Abstrakcyjna analiza harmoniczna . Tom. 2. ISBN 978-3-662-24595-8 . MR 0262773 .
•    Kirillov, Alexandre A. (1976) [1972]. Elementy teorii reprezentacji . Grundlehren der Mathematischen Wissenschaften. Tom. 220. Berlin, Nowy Jork: Springer-Verlag . ISBN 978-0-387-07476-4 . MR 0412321 .
•   Loomis, Lynn H. (1953). Wprowadzenie do abstrakcyjnej analizy harmonicznej . D. van Nostrand Co. ISBN 978-0486481234 .
•   Morris, SA (1977). Dualizm Pontryagina i struktura lokalnie zwartych grup abelowych . Wydawnictwo Uniwersytetu Cambridge . ISBN 978-0521215435 .
•   Oniszczik, AL (1984). Dualizm Pontrjagina . Encyklopedia matematyki . Tom. 4. s. 481–482. ISBN 978-1402006098 .
•   Reitera, Hansa (1968). Klasyczna analiza harmoniczna i grupy lokalnie zwarte . ISBN 978-0198511892 .
•   Rudin, Walter (1962). Analiza Fouriera na grupach . D. van Nostrand Co. ISBN 978-0471523642 .
•   Timmermann, T. (2008). Zaproszenie do grup kwantowych i dualności - od algebr Hopfa do unitarnych multiplikatywnych i nie tylko . Podręczniki EMS z matematyki, Europejskie Towarzystwo Matematyczne. ISBN 978-3-03719-043-2 .
• Kustermans, J.; Vaes, S. (2000). „Lokalnie zwarte grupy kwantowe” . Annales Scientifiques de l'École Normale Supérieure . 33 (6): 837–934. doi : 10.1016/s0012-9593(00)01055-7 .
•   Ardanza-Trevijano, Sergio; Chasco, María Jesús (2005). „Dwoistość Pontryagina kolejnych granic topologicznych grup abelowych”. Journal of Algebra Czysta i Stosowana . 202 (1–3): 11–21. doi : 10.1016/j.jpaa.2005.02.006 . HDL : 10171/1586 . MR 2163398 .
•   Chasco, Maria Jesús; Dikranjan, Dikran; Martín-Peinador, Elena (2012). „Badanie dotyczące zwrotności abelowych grup topologicznych” . Topologia i jej zastosowania . 159 (9): 2290–2309. doi : 10.1016/j.topol.2012.04.012 . MR 2921819 .
•   Kaplan, Samuel (1948). „Rozszerzenia dualności Pontrjagina. Część I: produkty nieskończone”. Duke Mathematical Journal . 15 : 649–658. doi : 10.1215/S0012-7094-48-01557-9 . MR 0026999 .
•   Kaplan, Samuel (1950). „Rozszerzenia dualności Pontrjagina. Część II: granice bezpośrednie i odwrotne”. Duke Mathematical Journal . 17 : 419–435. doi : 10.1215/S0012-7094-50-01737-6 . MR 0049906 .
•   Venkataraman, Rangachari (1975). „Rozszerzenie dualności Pontryagina”. Mathematische Zeitschrift . 143 (2): 105–112. doi : 10.1007/BF01187051 . S2CID 123627326 .
•   Martín-Peinador, Elena (1995). „Odblaskowa dopuszczalna grupa topologiczna musi być lokalnie zwarta”. Proceedings of American Mathematical Society . 123 (11): 3563–3566. doi : 10.2307/2161108 . hdl : 10338.dmlcz/127641 . JSTOR 2161108 .
• Roeder, David W. (1974). „Teoria kategorii zastosowana do dualności Pontryagina” . Pacific Journal of Mathematics . 52 (2): 519–527. doi : 10.2140/pjm.1974.52.519 .
•    Smith, Marianne F. (1952). „Twierdzenie Pontrjagina o dwoistości w przestrzeniach liniowych”. Roczniki matematyki . 56 (2): 248–253. doi : 10.2307/1969798 . JSTOR 1969798 . MR 0049479 .
• Waterhouse, William C. (1968). „Podwójne grupy przestrzeni wektorowych” . Pacific Journal of Mathematics . 26 (1): 193–196. doi : 10.2140/pjm.1968.26.193 .