Klasyfikacja Bianchiego

W matematyce klasyfikacja Bianchiego zawiera listę wszystkich rzeczywistych trójwymiarowych algebr Liego ( aż do izomorfizmu ). Klasyfikacja zawiera 11 klas, z których 9 zawiera pojedynczą algebrę Liego, a dwie z nich zawierają rodzinę algebr Liego wielkości kontinuum. (Czasami dwie grupy są zawarte w nieskończonych rodzinach, co daje 9 zamiast 11 klas). Klasyfikacja jest ważna w geometrii i fizyce, ponieważ powiązane grupy Liego służą jako grupy symetrii trójwymiarowych rozmaitości riemannowskich . Jej nazwa pochodzi od Luigiego Bianchiego , który opracował ją w 1898 roku.

Termin „klasyfikacja Bianchiego” jest również używany do podobnych klasyfikacji w innych wymiarach oraz do klasyfikacji złożonych algebr Liego .

Klasyfikacja w wymiarze mniejszym niż 3

• ⁰ Wymiar 0: Jedyną algebrą Liego jest abelowa algebra Liego R .
• Wymiar 1: Jedyną algebrą Liego jest abelowa algebra Liego R ¹ , z zewnętrzną grupą automorfizmu multiplikatywną grupą niezerowych liczb rzeczywistych.
• Wymiar 2: Istnieją dwie algebry Liego:
  • (1) Abelowa algebra Liego R ² , z zewnętrzną grupą automorfizmów GL ₂ ( R ) .
  • (2) Rozwiązywalna algebra Liego macierzy górnych trójkątów 2×2 o śladzie 0. Ma trywialne centrum i trywialną zewnętrzną grupę automorfizmów. Powiązana prostu połączona grupa Liego jest grupą afiniczną linii.

Klasyfikacja w wymiarze 3

Wszystkie trójwymiarowe algebry Liego inne niż typy VIII i IX można skonstruować jako półprosty iloczyn R ² i R , przy czym R działa na R ² przez jakąś macierz M 2 na 2 . Różne typy odpowiadają różnym typom macierzy M , jak opisano poniżej.

• Typ I : Jest to abelowa i jednomodułowa algebra ^Liego R3 . Grupa o prostym połączeniu ma centrum R ³ i zewnętrzną grupę automorfizmów GL ₃ ( R ). Dzieje się tak, gdy M wynosi 0.
• Typ II : Algebra Heisenberga , która jest nilpotentna i jednomodułowa. Prosto spójna grupa ma centrum R i zewnętrzną grupę automorfizmów GL ₂ ( R ). Dzieje się tak, gdy M jest nilpotentne, ale nie jest równe 0 (wszystkie wartości własne wynoszą 0).
• Typ III : Ta algebra jest iloczynem R i dwuwymiarowej nieabelowej algebry Liego. (Jest to przypadek graniczny typu VI, w którym jedna wartość własna staje się zerem). Jest rozwiązywalny i nie jest jednomodułowy. Grupa prosto spójna ma centrum R , a zewnętrzną grupę automorfizmów grupę niezerowych liczb rzeczywistych. Macierz M ma jedną zerową i jedną niezerową wartość własną.
• Typ IV : Algebra generowana przez [ y , z ] = 0, [ x , y ] = y , [ x , z ] = y + z . Jest rozwiązywalny i nie jest jednomodułowy. Prosto spójna grupa ma trywialne centrum i zewnętrzną grupę automorfizmów, iloczyn liczb rzeczywistych i grupę rzędu 2. Macierz M ma dwie równe niezerowe wartości własne, ale nie jest diagonalizowalna .
• Wpisz V : [ y , z ] = 0, [ x , y ] = y , [ x , z ] = z . Rozwiązywalne i niejednomodułowe. (Ograniczający przypadek typu VI, w którym obie wartości własne są równe.) Grupa prosto spójna ma trywialne centrum i zewnętrzną grupę automorfizmów elementów GL ₂ ( R ) wyznacznika +1 lub -1. Macierz M ma dwie równe wartości własne i jest diagonalizowalna.
• Typ VI : Rodzina nieskończona: iloczyny półproste R ² przez R , gdzie macierz M ma niezerowe różne rzeczywiste wartości własne z niezerową sumą. Algebry są rozwiązywalne i nie są jednomodułowe. Prosto spójna grupa ma trywialne centrum i zewnętrzną grupę automorfizmu iloczyn niezerowych liczb rzeczywistych i grupę rzędu 2.
• Typ VI : ₀ Ta algebra Liego jest półprostym iloczynem R2 przez R , gdzie macierz M ma niezerowe różne rzeczywiste wartości własne z sumą zerową ^. Jest rozwiązywalny i jednomodułowy. Jest to algebra Liego dwuwymiarowej grupy Poincarégo , grupy izometrii dwuwymiarowej przestrzeni Minkowskiego . Po prostu połączona grupa ma trywialne centrum i zewnętrzną grupę automorfizmu, iloczyn dodatnich liczb rzeczywistych z grupą dwuścienną rzędu 8.
• Typ VII : Rodzina nieskończona: iloczyny półproste R ² przez R , gdzie macierz M ma nierzeczywiste i nieurojone wartości własne. Rozwiązywalne i niejednomodułowe. Prosto spójna grupa ma trywialne centrum, a zewnętrzna grupa automorfizmu niezerowe liczby rzeczywiste.
• Typ VII ₀ : Półprosty iloczyn R ² przez R , gdzie macierz M ma niezerowe urojone wartości własne. Rozwiązywalne i jednomodułowe. To jest algebra Liego grupy izometrii płaszczyzny. Prosto spójna grupa ma centrum Z i zewnętrzną grupę automorfizmu iloczyn niezerowych liczb rzeczywistych i grupę rzędu 2.
• Typ VIII : Algebra Liego sl ₂ ( R ) bezśladowych macierzy 2 na 2, związana z grupą SL ₂ ( R ) . Jest prosty i jednomodułowy. Po prostu połączona grupa nie jest grupą macierzową; jest oznaczony przez ${\ Displaystyle {\ overline {{\ mbox {SL}} (2, \ mathbf {R}}}}} ,$ ma środek Z , a jego zewnętrzna grupa automorfizmów ma rząd 2.
• Typ IX : Algebra Liego grupy ortogonalnej O ₃ ( R ). Jest oznaczony przez 𝖘𝖔(3) i jest prosty i jednomodułowy. Odpowiednia grupa prosto spójna to SU(2) ; ma środek rzędu 2 i trywialną zewnętrzną grupę automorfizmu i jest grupą spinową .

Klasyfikacja trójwymiarowych złożonych algebr Liego jest podobna, z wyjątkiem tego, że typy VIII i IX stają się izomorficzne, a typy VI i VII stają się częścią jednej rodziny algebr Liego.

Połączone trójwymiarowe grupy Liego można sklasyfikować w następujący sposób: są one ilorazem odpowiedniej prosto połączonej grupy Liego przez dyskretną podgrupę środka, więc można to odczytać z powyższej tabeli.

hipotezy geometryzacyjnej Thurstona . Dokładniej, siedem z 8 geometrii można zrealizować jako metrykę niezmienniczą z lewej strony na grupie po prostu połączonej (czasami na więcej niż jeden sposób). Geometria Thurston typu S ² × R nie może być zrealizowana w ten sposób.

Stałe struktury

Każda z trójwymiarowych przestrzeni Bianchiego dopuszcza zestaw trzech pól wektorowych Killing, które są zgodne z następującą właściwością: ${\ Displaystyle \ xi _ {i} ^ {(a)}}$

${\ Displaystyle \ lewo ({\ Frac {\ częściowe \$

gdzie „ $antysymetryczny$ strukturalne ” grupy tworzą stały rzędu w dwóch dolnych indeksach Dla dowolnej trójwymiarowej przestrzeni Bianchiego jest dana relacja do za ${\ ab} ^ {c}}$

$Displaystyle C _ {\ ab} ^ {c} = \ varepsilon _ {abd} n ^ {cd} - \ delta _{a}^{c}a_{b}+\delta _{b}^{c}a_{a}}$

gdzie $}}$$abd$ to symbol Levi-Civita , to Kroneckera , a wektor ${\ Displaystyle a_ {a} = (a, 0,0)}$ i tensor przekątnej $\ Displaystyle n ^ {cd}}$ są opisane w poniższej tabeli, gdzie ${\ Displaystyle n ^ {(i)}}$ daje ja th wartość własna n $\ Displaystyle n ^ {cd}}$ ; parametr a przebiega po wszystkich dodatnich liczbach rzeczywistych :

typu Bianchiego	${\ displaystyle a}$	${\ Displaystyle n ^ {(1)}}$	${\ Displaystyle n ^ {(2)}}$	${\ Displaystyle n ^ {(3)}}$	klasa	notatki	graficzny (ryc. 1)
I	0	0	0	0	A	opisuje przestrzeń euklidesową	u źródła
II	0	1	0	0	A		interwał [0,1] wzdłuż ${\ Displaystyle n ^ {(1)}}$
III	1	0	1	-1	B	podprzypadek typu VI a z za $\ displaystyle a = 1}$	rzutuje na czwartą ćwiartkę płaszczyzny a = 0
IV	1	0	0	1	B		pionowa otwarta ściana między pierwszą a czwartą ćwiartką płaszczyzny a = 0
V	1	0	0	0	B	ma hiper- pseudosferę jako przypadek szczególny	przedział (0,1] wzdłuż osi a
VI0	0	1	-1	0	A		czwartej ćwiartce płaszczyzny poziomej
VI a	${\ displaystyle a}$	0	1	-1	B	kiedy ${\ displaystyle a = 1}$ , odpowiednik typu III	rzutuje na czwartą ćwiartkę płaszczyzny a = 0
VII0	0	1	1	0	A	ma przestrzeń euklidesową jako przypadek szczególny	pierwsza ćwiartka płaszczyzny poziomej
VII a	${\ displaystyle a}$	0	1	1	B	ma hiper-pseudosferę jako szczególny przypadek	rzutuje na pierwszą ćwiartkę płaszczyzny a = 0
VIII	0	1	1	-1	A		szósty oktant
IX	0	1	1	1	A	ma hipersferę jako przypadek szczególny	drugi oktant

Rysunek 1. Przestrzeń parametrów jako 3-płaszczyzna (klasa A) i ortogonalna połówka 3-płaszczyzny (klasa B) w R ⁴ o współrzędnych ( n ⁽¹⁾ , n ⁽²⁾ , n ⁽³⁾ , a ), przedstawiający kanonicznych przedstawicieli każdego typu Bianchi.

Standardową klasyfikację Bianchiego można wyprowadzić ze stałych strukturalnych w następujących sześciu krokach:

1. 
   Do za b do = - do b za do ${c} = - C_ {ba} ^ {c}}$ dziewięć niezależnych stałych ${\ Displaystyle C_ {ab}^{c}}$ . Można je równoważnie przedstawić za pomocą dziewięciu składowych dowolnej macierzy stałej C ^ab :
   
   ${\ Displaystyle C_ {ab} ^ {c} = \ varepsilon _ {abd} C ^ {dc},} gdzie$ ε _abd jest całkowicie antysymetrycznym trójwymiarowym symbolem Levi-Civita (ε ₁₂₃ = 1). Podstawienie tego wyrażenia na tożsamość Jacobiego $do$ , że $C^{bd}C^{ac}=0.}$$Displaystyle \ varepsilon _ {$
2. 
   
   
   Stałe struktury można przekształcić jako: ${\ Displaystyle C ^ {ab} = \ lewo (\ det {A} \ prawo) ^ {- 1} A_ {m} ^ {a} A_ {n} ^ {b} {\ ostry {C}} ^ { mn}.}$ Pojawienie się det A w tym wzorze wynika z faktu, że symbol ε _abd przekształca się jako gęstość tensorowa: ${\ Displaystyle \ varepsilon _ {abc} = \ lewo (\ det {A} \ prawej) D_ {a} ^ {m} D_ {b}$ , gdzie έ _mnd ≡ ε _mnd . Dzięki tej transformacji zawsze można sprowadzić macierz C ^ab do postaci:
   ${\ Displaystyle C ^ {ab} = {\ rozpocząć {bmatrix} n_ {1} i 0 i 0 \\ 0 i C ^ {22} i C ^ {23} \\ 0 i C ^ {32} i C ^ {33} \ koniec {bmatrix}} .}$ Po takim wyborze nadal mamy swobodę dokonywania transformacji triad, ale z ograniczeniami ${\ Displaystyle A_ {2} ^ {1} = A_ {3} ^ {1} = 0 }$ i ${\ Displaystyle A_ {1} ^ {2} = A_ {1} ^ {3} = 0.}$
3. 
   Teraz tożsamości Jacobiego dają tylko jedno ograniczenie: ${\ Displaystyle \ lewo (C ^ {23} -C ^ {32} \ prawej) n_ {1} = 0.}$
4. Jeśli n ₁ ≠ 0 to do ²³ - do ³² = 0 i przez pozostałe przekształcenia z ${\ Displaystyle A _ {\ bar {b}} ^ { \bar {a}}\neq 0,\quad {\bar {a}},{\bar {b}}={\bar {2}},{\bar {3}}} , macierz 2 ×$ 2 do za $bar {b}}}} w$
   
   Kabina ^może być ukośna. Wtedy ${\ Displaystyle C ^ {ab} = {\ rozpocząć {bmatrix} n_ {1}&0&0 \\0&n_ {2}&0\\0&0&n_ {3}\end {bmatrix}}.} Warunek diagonalności dla C$ ab jest ^zachowany pod przekształcenia z przekątną ${\ Displaystyle A_ {b} ^ {a}}$ . W ramach tych przekształceń trzy parametry n ₁ , n ₂
   
   , n ₃ zmienia się w następujący sposób: ${\ Displaystyle n_ {a} = \ lewo (A_ {1} ^ {1} A_ {2} ^ {2} A_ {3} ^ {3} \ prawo) \ lewo (A_ {a} ^ {a} \ dobrze)^{2}{\acute {n}}_{a},{\text{bez sumowania po}}\ a.}$ Dzięki tym przekształceniom diagonalnym moduł dowolnego n _a (jeśli nie jest zerem) można zrównać z jednością. Biorąc pod uwagę, że jednoczesna zmiana znaku wszystkich n _a nie daje nic nowego, dochodzimy do następujących niezmiennie różnych zbiorów dla liczb n ₁ , n ₂ , n ₃ (niezmiennie różnych w tym sensie, że nie można przejść od jeden do drugiego przez jakąś transformację triady
   ${\ Displaystyle e_ {a} ^ {\ bar {a}} = A _ {\ bar {b}} ^ {\ bar {a}} e_ {a} ^ {\ bar {b}}}), to$ znaczy następujące różne typy przestrzeni jednorodnych z macierzą ${\ Displaystyle {\ rozpocząć {macierz} Bianchi \ IX &: & (n_ {1}, n_ {2}, n_ {3}) & = & (1,1,1), \\ Bianchi \ VIII&: & (n_ {1},n_{2},n_{3})&=&(1,1,-1),\\Bianchi\ VII_{0}&:&(n_{1},n_{2},n_{ 3})&=&(1,1,0),\\Bianchi\ VI_{0}&:&(n_{1},n_{2},n_{3})&=&(1,-1, 0),\\Bianchi\ II&:&(n_{1},n_{2},n_{3})&=&(1,0,0).\end{macierz}}}$ C ^ab :
5. ₀₀ Rozważmy teraz przypadek n ₁ = 0. W takim przypadku może się również zdarzyć, że C ²³ – C ³² = 0. To powraca do sytuacji analizowanej już w poprzednim kroku, ale z dodatkowym warunkiem n ₁ = 0. Teraz wszystko zasadniczo różne typy dla zbiorów n ₁ , n ₂ , n ₃ to (0, 1, 1), (0, 1, −1), (0, 0, 1) i (0, 0, 0). Pierwsze trzy powtarzają typy VII , VI , II
   . W rezultacie ${\ Displaystyle Bianchi \ ja \: \ (n_ {1}, n_ {2}, n_ {3}) \ = \ (0,0,0).}$ tylko jeden nowy typ:
6. Pozostał tylko przypadek n ₁ = 0 i do ²³ - do ³² ≠ 0. Teraz macierz 2 × 2 do $\ Displaystyle C ^ {{\ bar { a}}{\bar {b}}}({\bar {a}},{\bar {b}}=2,3)} jest niesymetryczne i nie można go przekształcić w przekątną$ przez przekształcenia za pomocą ${\ Displaystyle A _ {\ bar {b}} ^ {\ bar {a}} \ neq 0}$
   
   . Jednak jego symetryczną część można przekątować, to znaczy macierz 3 × 3 C ^ab można sprowadzić do postaci: ${\ Displaystyle C ^ {ab} = {\ begin{bmatrix}0&0&0\\0&n_{2}&a\\0&-a&n_{3}\end{bmatrix}},}$ gdzie a jest dowolną liczbą. Po wykonaniu tej czynności pozostaje jeszcze możliwość wykonywania przekształceń z przekątną
   ${\ Displaystyle A _ {\ bar {b}} ^ {\ bar {a}}}$ , przy czym ilości n ₂ , n ₃ i zmiana w następujący sposób:
   ${\ Displaystyle n_ {2} = \ lewo (A_ {1} ^ {1} A_ {2} ^ {2} A_ {3} ^ {3} \ prawo) ^ {-1} \ lewo (A_ {2} ^{2}\right)^{2}{\ostre {n}}_{2},\quad n_{3}=\left(A_{1}^{1}A_{2}^{2}A_ {3}^{3}\right)^{-1}\left(A_{3}^{3}\right)^{2}{\acute {n}}_{3},\quad a=\ left(A_{1}^{1}\right)^{-1}{\acute {a}}.}$ Wzory te pokazują, że dla niezerowego n ₂ , n ₃ , za , kombinacja a ² ( n ₂ n ₃ ) ⁻¹ jest wielkością niezmienną. Wybierając , ${\ Displaystyle A_ {3} ^ {3} \ lewo (A_ {2} ^ {2} \ prawo) ^ {-1}}$ narzucić warunek a > 0 $wykonaniu tej$ wybór znaku
   pozwala na jednoczesną zmianę obu znaków n ₂ i n ₃ , czyli zbiór ( n ₂ , n ₃ ) jest równoważny zbiorowi (− n ₂ , − n ₃ ). Wynika z tego, że istnieją cztery różne możliwości:
   
   ${\ Displaystyle (a, n_ {2}, n_ {3}) = (a,0,0), (a,0,1), (a,1,1), (a,1, -1). }$ W przypadku pierwszych dwóch liczbę a można przekształcić w jedność, wybierając parametry i ${\ Displaystyle A_ {1} ^ {1}}$ i
   
   ${\ Displaystyle A_ {3} ^ {3} \ lewo (A_ {2} ^ {2} \ prawo) ^ {-1}}$ . W przypadku dwóch drugich możliwości oba te parametry są już ustalone, a a pozostaje niezmienną i dowolną liczbą dodatnią. Historycznie te cztery typy przestrzeni jednorodnych zostały sklasyfikowane jako ${\ Displaystyle {\ rozpocząć {macierz} Bianchi \ V&: & n_ {1} = 0, \ (a, n_ {2}, n_ {3}) & = & (1,0,0), \\ Bianchi \ IV& :&n_{1}=0,\ (a,n_{2},n_{3})&=&(1,0,1),\\Bianchi\ VII&:&n_{1}=0,\ (a, n_{2},n_{3})&=&(a,1,1),\\Bianchi\ III&:&n_{1}=0,\ (a,n_{2},n_{3})&= &(1,1,-1),\\Bianchi\ VI&:&n_{1}=0,\ (a,n_{2},n_{3})&=&(a,1,-1).\ end{macierz}}}$ Typ III to po prostu szczególny przypadek typu VI odpowiadający a = 1. Typy VII i VI ₀₀ zawierają nieskończoność niezmiennie różnych typów algebr odpowiadających arbitralności ciągłego parametru a . Typ VII jest szczególnym przypadkiem VII odpowiadającym a = 0, podczas gdy typ VI jest szczególnym przypadkiem VI odpowiadającym również a = 0.

Krzywizna przestrzeni Bianchiego

Przestrzenie Bianchiego mają tę właściwość, że ich tensory Ricciego można rozłożyć na iloczyn wektorów bazowych związanych z przestrzenią i tensora niezależnego od współrzędnych.

Dla danej metryki :

${\ Displaystyle ds ^ {2} = \ gamma _ {ab} \ xi _ {i} ^ {(a)} \xi _{k}^{(b)}dx^{i}dx^{k}}$

$ja$ gdzie 1-formy $}}$ , tensor $Ricciego$ R jest dana przez:

${\ Displaystyle R_ {ik} = R_ {(a) (b)} \ xi _ {i} ^ {(a)$

$} \left[C_{\ \ b}^{cd}\left(C_{cda}+C_{dca}\right)+C_{\ cd}^{c}\left(C_{ab}^{\ \ d }+C_{ba}^{\ \ d}\right)-{\frac {1}{2}}C_{b}^{\ cd}C_{acd}\right]}$

gdzie indeksy na stałych strukturalnych są podnoszone i obniżane z ${\ displaystyle \ gamma _ {ab}}$ , co nie jest funkcją ${\ displaystyle x ^ {i}}$ .

Zastosowanie kosmologiczne

W kosmologii ta klasyfikacja jest stosowana dla jednorodnej czasoprzestrzeni o wymiarze 3+1. Trójwymiarowa grupa Liego jest grupą symetrii trójwymiarowego przestrzennego wycinka, a metryka Lorentza spełniająca równanie Einsteina jest generowana przez zmianę składowych metrycznych w funkcji t. Friedmanna – Lemaître – Robertsona – Walkera są $i$ , które są szczególnymi przypadkami typów I, V, IX. Modele Bianchiego typu I obejmują metrykę Kasnera jako przypadek specjalny. Kosmologie Bianchiego IX obejmują metrykę Tauba . Jednak dynamika w pobliżu osobliwości jest w przybliżeniu regulowana przez serię kolejnych okresów Kasnera (Bianchi I). Skomplikowana dynamika, która zasadniczo sprowadza się do ruchu bilardowego w części przestrzeni hiperbolicznej, wykazuje chaotyczne zachowanie i nazywa się Mixmaster ; jej analizę określa się jako analizę BKL za Belinskim, Chalatnikowem i Lifshitzem. Nowsze prace ustaliły związek teorii (super-) grawitacji w pobliżu przestrzennej osobliwości (granica BKL) z algebrami Lorentza Kaca-Moody'ego , Grupy Weyla i hiperboliczne grupy Coxetera . Inne nowsze prace dotyczą dyskretnego charakteru mapy Kasnera i ciągłego uogólniania. W przestrzeni, która jest zarówno jednorodna, jak i izotropowa, metryka jest określona całkowicie, pozostawiając wolny tylko znak krzywizny. Przyjęcie jedynie jednorodności przestrzeni bez dodatkowej symetrii, takiej jak izotropia, pozostawia znacznie większą swobodę w doborze metryki. Poniższe dotyczy przestrzennej części metryki w danej chwili czasu t, zakładając ramkę synchroniczną, tak że t jest tym samym zsynchronizowanym czasem dla całej przestrzeni.

Jednorodność implikuje identyczne właściwości metryczne we wszystkich punktach przestrzeni. Dokładna definicja tego pojęcia polega na rozważeniu zbiorów przekształceń współrzędnych, które przekształcają przestrzeń w siebie, tj. pozostawiają jej metrykę bez zmian: jeżeli element liniowy przed transformacją

${\ Displaystyle dl ^ {2} = \ gamma _ {\ alfa \ beta} \ lewo (x ^ {1} ,x^{2},x^{3}\right)dx^{\alfa }dx^{\beta},}$

to po przekształceniu jest ten sam element liniowy

${\ Displaystyle dl ^ {2} = \ gamma _ {\ alfa \ beta} \ lewo ( x^{\liczba pierwsza 1},x^{\liczba pierwsza 2},x^{\liczba pierwsza 3}\right)dx^{\liczba pierwsza \alpha}dx^{\liczba pierwsza \beta},}$

z tą samą funkcjonalną zależnością γ _αβ od nowych współrzędnych. (Aby zapoznać się z bardziej teoretyczną i niezależną od współrzędnych definicją przestrzeni jednorodnej, patrz przestrzeń jednorodna ). Przestrzeń jest jednorodna, jeśli dopuszcza zbiór przekształceń ( grupę ruchów ), które doprowadzają dowolny punkt do położenia dowolnego innego punktu. Ponieważ przestrzeń jest trójwymiarowa, różne przekształcenia grupy są oznaczone trzema niezależnymi parametrami.

Rysunek 2. Triada e ^{( a )} ( e ⁽¹⁾ , e ⁽²⁾ , e ⁽³⁾ ) jest afinicznym układem współrzędnych (w tym w szczególnym przypadku kartezjańskim układem współrzędnych), którego współrzędne są funkcjami współrzędnych krzywoliniowych x _α (x ₁ , x ₂ , x ₃ ).

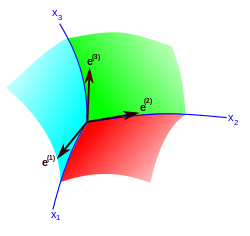
W przestrzeni euklidesowej jednorodność przestrzeni wyraża się niezmiennością metryki przy równoległych przemieszczeniach ( translacjach ) kartezjańskiego układu współrzędnych . Każde przesunięcie jest określone przez trzy parametry — składowe wektora przemieszczenia początku współrzędnych. Wszystkie te przekształcenia pozostawiają niezmienne trzy niezależne różniczki ( dx , dy , dz ), z którego zbudowany jest element liniowy. W ogólnym przypadku nieeuklidesowej przestrzeni jednorodnej przekształcenia jej grupy ruchów ponownie pozostawiają niezmiennicze trzy niezależne liniowe formy różniczkowe , które jednak nie sprowadzają się do różnic całkowitych żadnych funkcji współrzędnych. Formy te $)$ zapisywane jako gdzie indeks łaciński ( niezależne wektory ( wektory te nazywane są a pole ramki lub triada. Greckie litery oznaczają trzy przestrzenne współrzędne krzywoliniowe . Przestrzenny niezmiennik metryczny jest konstruowany dla danej grupy ruchów z wykorzystaniem powyższych postaci:

${\ Displaystyle dl ^ {2} = \ eta _ {ab} \ lewo (e_ {\ alfa} ^{(a)}dx^{\alpha}\right)\left(e_{\beta}^{(b)}dx^{\beta}\right)}$

 

 

 

 

()

tj. tensor metryczny jest

${\ Displaystyle \ gamma _ {\ alfa \ beta} = \ eta _ {ab} e_ {\ alfa} ^ {(a)} e_ {$

 

 

 

 

()

gdzie współczynniki η _ab , które są symetryczne we wskaźnikach a i b , są funkcjami czasu. Wybór wektorów bazowych jest podyktowany właściwościami symetrii przestrzeni i generalnie te wektory bazowe nie są ortogonalne (tak, że macierz η _ab nie jest diagonalna).

Odwrotna trójka wektorów ${\ Displaystyle e_ {(a)} ^ {\ alfa}}$ wprowadzana za pomocą delty Kroneckera mi

${\ Displaystyle e_ {(a)} ^ {\ alfa} e_ {\ alfa} ^ {(b)} = \ delta _ {a} ^ {b} ;\quad e_{(a)}^{\alpha}e_{\beta}^{(a)}=\delta _{\alpha}^{\beta}}$

 

 

 

 

()

W przypadku trójwymiarowym relację między dwiema trójkami wektorowymi można zapisać jawnie

${\ Displaystyle \ mathbf {e} _ {(1)} = {\ Frac {1} {v}} \ mathbf {e} ^ {(2)} \ razy \ mathbf {e} ^ {(3)}, \quad \mathbf {e} _{(2)}={\frac {1}{v}}\mathbf {e} ^{(3)}\times \mathbf {e} ^{(1)},\ quad \mathbf {e} _{(3)}={\frac {1}{v}}\mathbf {e} ^{(1)}\times \mathbf {e} ^{(2)},}$

 

 

 

 

()

jest objętość v

${\ Displaystyle v = \ lewo \ vert e _ {\ alfa} ^ {(a)} \ prawo \ vert = \ mathbf {e} ^ {(1 )}\cdot \mathbf {e} ^{(2)}\times \mathbf {e} ^{(3)},}$

mi ( _{za ) i} i mi ^{( za )} traktowane jako wektory kartezjańskie ze składowymi ${\ Displaystyle e_ {(a)} ^ {\ alfa}}$ mi $^{(a)}} .$$\ Displaystyle e_ {\ alfa}$ odpowiednio Wyznacznik tensora metrycznego eq . 6b to γ ​​= η v ² , gdzie η jest wyznacznikiem macierzy η _ab .

Wymagane warunki jednorodności przestrzeni to

${\ Displaystyle \ lewo ({\ Frac {\ częściowe e_ {\ alfa} ^ {(c)}} {\ częściowe x ^ {\ beta}}} - {\ Frac {\ częściowe e_ {\ beta} ^ {( c)}}{\częściowe x^{\alpha}}}\right)e_{(a)}^{\alpha}e_{(b)}^{\beta}=C_{ab}^{c}. }$

 

 

 

 

()

Stałe $_$ grupy . _

Dowód równ . 6e

Niezmienniczość form różniczkowych oznacza, że ${\ Displaystyle e_ {\ alfa} ^ {(a)} dx ^ {\ alfa}}$ ${\ Displaystyle e_ {\ alfa} ^ {(a)} (x) dx ^ {\ alfa} = e_ {\alpha}^{(a)}(x^{\prime})dx^{\prime \alpha}}$ gdzie po obu stronach równania są te same funkcje odpowiednio starych i nowych współrzędnych mi $(a)}}$$,$ równanie ′ ${\ Displaystyle dx ^ {\ pierwsza \ beta} = {\ Frac {\ częściowa x ^ {\ pierwsza \ beta}} {\ częściowa x ^ {\ alfa}}} dx ^ {\ alfa},} i porównanie$ współczynników te same różniczki dx α , można znaleźć ${\ Displaystyle {\ Frac {\ częściowy x ^ {\ pierwszy \ beta}} {\ częściowy x ^ {\ alfa}}} = e_ {(a)} ^ {\ beta} (x ^ {\ pierwszy}) e_ {\alfa}^{(a)}(x).}$ $,$ określają funkcje danej ramki Aby równania te były całkowalne, muszą spełniać identyczne warunki ${\ Displaystyle {\ Frac {\ częściowy ^ {2} x ^ {\ pierwszy \ beta}} {\ częściowy x ^ {\ alfa} \ częściowy x ^ {\ gamma}}} = {\ Frac {\ częściowy ^ { 2}x^{\pierwsza \beta }}{\częściowa x^{\gamma }\częściowa x^{\alfa }}}.}$ Obliczając pochodne, można znaleźć ${\ Displaystyle \ lewo [{\ Frac {\ częściowe e_ {(a)} ^ {\ beta} (x ^ {\ pierwsza})} {\ częściowe x ^ {\ pierwsza \ delta}}} e_ {(b) } ^{\delta }(x^{\prime })-{\frac {\częściowe e_{(b)}^{\beta}(x^{\prime })}{\częściowe x^{\prime \ delta }}}e_{(a)}^{\delta }(x^{\prime })\right]e_{\gamma }^{(b)}(x)e_{\alpha }^{(a) }(x)=e_{(a)}^{\beta }(x^{\prime })\left[{\frac {\częściowe e_{\gamma}^{(a)}(x)}{\ częściowe x ^ {\ alfa }}} - {\ frac {\ częściowe e_ {\ alfa} ^ {(a)} (x)} {\ częściowe x ^ {\ gamma}}} \ prawo].}$ Mnożenie obu stron równań przez ${\ Displaystyle e_ {(d)} ^ {\ alfa} (x) e_ {(c)}^{\gamma }(x)e_{\beta }^{(f)}(x^{\prime })} i przesunięcie różniczkowania z jednego czynnika na drugi za pomocą$ równania . 6c , otrzymujemy po lewej stronie: ${\ Displaystyle e _ {\ beta} ^ {(f)} (x ^ {\ pierwsza}} \ lewo [{\ Frac {\ częściowa e_ {(d)} ^ {\ beta} (x ^ {\ pierwsza}) }{\częściowa x^{\pierwsza \delta}}}e_{(c)}^{\delta}(x^{\pierwsza})-{\frac {\częściowa e_{(c)}^{\beta }(x^{\prime })}{\częściowa x^{\prime \delta }}}e_{(d)}^{\delta }(x^{\prime })\right]=e_{(c )}^{\beta}(x^{\prime})e_{(d)}^{\delta}(x^{\prime})\left[{\frac {\częściowe e_{\beta}^{ (f)}(x^{\prime })}{\częściowe x^{\prime \delta }}}-{\frac {\częściowe e_{\delta}^{(f)}(x^{\prime })}{\częściowe x^{\prime \beta }}}\right].}$ a po prawej to samo wyrażenie w zmiennej x . Ponieważ x i x' są dowolne, wyrażenie to musi zostać zredukowane do stałych, aby otrzymać równanie. 6e .

Mnożenie przez ${\ Displaystyle e_ {(c)} ^ {\ gamma}}$ równ . 6e można przepisać w formie

${\ Displaystyle e_ {(a)} ^ {\ alfa} {\ Frac {\ częściowe e_ {(b)} ^ {\ gamma}} {\ częściowe x ^ {\ alfa}}} -e_ {(b)} ^{\beta}}{\frac {\częściowe e_{(a)}^{\gamma}}{\częściowe x^{\beta}}}=C_{ab}^{c}e_{(c)}^ {\gamma}.}$

 

 

 

 

()

Równanie 6e można zapisać w postaci wektorowej jako

${\ Displaystyle \ mathbf {e} _ {(a)} \ razy \ mathbf {e} _ {(b)} {\ text{curl}}\mathbf {e} ^{(c)}=-C_{ab}^{c},}$

gdzie ponownie operacje na wektorach są wykonywane tak, jakby współrzędne x ^α były kartezjańskie. Używając równ. 6d , uzyskuje się

${\ Displaystyle {\ Frac {1} {v}} \ lewo (\ mathbf {e} ^ {(1)}} {\ tekst {curl}} \ mathbf {e} ^ {(1)} \ prawej) = C_{32}^{1},\quad {\frac {1}{v}}\left(\mathbf {e} ^{(2)}{\text{curl}}\mathbf {e} ^{( 1)}\right)=C_{13}^{1},\quad {\frac {1}{v}}\left(\mathbf {e} ^{(3)}{\text{curl}}\ mathbf {e} ^{(1)}\right)=C_{21}^{1}}$

 

 

 

 

()

i sześć innych równań otrzymanych przez cykliczną permutację indeksów 1, 2, 3.

Stałe struktury są antysymetryczne w swoich dolnych indeksach, jak wynika z ich definicji eq. 6e : $\ Displaystyle C_ {ab} ^ {c} = - C_ {ba} ^ {c}}$ . Inny warunek dotyczący stałych struktury można uzyskać, zauważając, że równ. 6f można zapisać w postaci relacji komutacyjnych

${\ Displaystyle \ lewo [X_ {a}, X_ {b} \ prawej] \ równoważnik X_ {a} X_$

 

 

 

 

()

dla liniowych operatorów różniczkowych

${\ Displaystyle X_ {a} = e_ {(a)} ^ {\ alfa} {\ Frac {\ częściowy} {\ częściowy x ^ {\ alfa}}}}$

 

 

 

 

()

W matematycznej teorii grup ciągłych ( grupy Liego ) operatory X _a spełniają warunki równ. 6h nazywane są generatorami grupy . Teoria grup Liego wykorzystuje operatory zdefiniowane za pomocą $} }^{\alfa}}$ zabijania ${\ Displaystyle \ xi _ {(a)} ^ {$ triad . Ponieważ w metryce synchronicznej żaden z γ _αβ składowe zależą od czasu, wektory zabijania (triady) są podobne do czasu.

Warunki równ. 6h wynika z tożsamości Jacobiego

${\ Displaystyle [[X_ {a}, X_ {b}],X_{c}]+[[X_{b},X_{c}],X_{a}]+[[X_{c},X_{a}],X_{b}]=0 }$

i mieć formę

${e} C_ {ec} ^ {d} + C_$

 

 

 

 

()

$zaletą$ użycie zamiast stałych trójindeksowych zestawu wielkości dwuindeksowych, otrzymanych przez

$\ Displaystyle C_ {ab} ^ {c} = e_ {abd} C ^ {dc}$

 

 

 

 

()

gdzie e _abc = e ^abc jest jednostkowym symbolem antysymetrii (gdzie e ₁₂₃ = +1). Przy tych stałych relacje komutacyjne równ. 6h są zapisane jako

$\ Displaystyle e ^ {abc} X_ {b} X_ {c} = C ^ {reklama} X_ {d}$

 

 

 

 

()

Właściwość antysymetrii jest już uwzględniona w definicji eq. 6k , natomiast majątek eq. 6j przyjmuje formę

${\ Displaystyle e_ {bcd} C ^ {cd} C ^ {ba}$

 

 

 

 

()

Wybór trzech wektorów ramek w formach różniczkowych ${\ Displaystyle e_ {\ alfa} ^ {(a)} dx ^ {\ alfa}}$ (a wraz z nimi operatory X _a ) jest nieunikalny. Można je poddać dowolnej transformacji liniowej o stałych współczynnikach:

${\ Displaystyle \ mathbf {e} _ {(a)} = A_ {a} ^ {b} \ mathbf {e} _ {(b)}.}$

 

 

 

 

()

Wielkości η _ab i C ^ab zachowują się jak tensory (są niezmienne) względem takich przekształceń.

Warunki równ. 6m to jedyne, które muszą spełniać stałe struktury. Ale wśród stałych dopuszczalnych przez te warunki istnieją zbiory równoważne w tym sensie, że ich różnica jest związana z transformacją typu eq. 6n . Kwestia klasyfikacji przestrzeni jednorodnych sprowadza się do wyznaczenia wszystkich nierównoważnych zbiorów stałych struktury. Można to zrobić, wykorzystując właściwości „tensorowe” wielkości C ^ab , za pomocą następującej prostej metody (CG Behr, 1962).

Asymetryczny tensor C ^ab można rozłożyć na część symetryczną i część antysymetryczną. Pierwszy jest oznaczony przez n ^ab , a drugi jest wyrażony za pomocą wektora dualnego a _c :

${\ Displaystyle C ^ {ab} = n ^ {ab} + e ^ {abc} a_ {c}.}$

 

 

 

 

()

Podstawienie tego wyrażenia w równ. 6m prowadzi do stanu

${\ Displaystyle n ^ {ab} a_ {b} = 0.}$

 

 

 

 

()

Za pomocą przekształceń równ. 6n symetryczny tensor n ^ab można sprowadzić do postaci diagonalnej o wartościach własnych n ₁ , n ₂ , n ₃ . Z równania 6p wynika, że ​​wektor ab _. (jeśli istnieje) leży wzdłuż jednego z głównych kierunków tensora n ^ab , odpowiadającego wartości własnej zero Bez utraty ogólności można zatem ustawić a _b = ( a , 0, 0). następnie równ. 6p redukuje się do an ₁ = 0, tzn. jedna z wielkości a lub n ₁ musi być równa zeru. Tożsamości Jacobiego przybierają postać:

${\ Displaystyle [X_ {1}, X_ {2}] = - aX_ {2} + n_ {3} X_ {3}, \ quad [X_ {2}, X_ {3}] = n_ {1} X_ { 1},\quad [X_{3},X_{1}]=n_{2}X_{2}+aX_{3}.}$

 

 

 

 

()

Jedynymi pozostałymi swobodami są zmiany znaku operatorów X _a i ich mnożenie przez dowolne stałe. Pozwala to jednocześnie zmienić znak wszystkich n _a , a także uczynić wielkość dodatnią (jeśli jest różna od zera). Również wszystkie stałe struktury można sprowadzić do ±1, jeśli co najmniej jedna z wielkości a , n ₂ , n ₃ zniknie. Ale jeśli wszystkie trzy z tych wielkości różnią się od zera, przekształcenia skali pozostawiają niezmienniczy stosunek h = za ² ( n ₂ n ₃ ) ^-1 .

W ten sposób dochodzi się do klasyfikacji Bianchiego wymieniającej możliwe typy przestrzeni jednorodnych sklasyfikowanych według wartości a , n ₁ , n ₂ , n ₃ , którą graficznie przedstawiono na rys. 3. W przypadku klasy A ( a = 0) typ IX ( n ⁽¹⁾ =1, n ⁽²⁾ =1, n ⁽³⁾ =1) jest reprezentowany przez oktant 2, typ VIII ( n ⁽¹⁾ =1, n ⁽²⁾ =1, n ⁽³⁾ =–1) jest reprezentowany przez oktant 6, natomiast typ VII ₀ ( n ⁽¹⁾ =1, n ⁽²⁾ =1, n ⁽³⁾ =0) jest reprezentowany przez pierwszą ćwiartkę płaszczyzny poziomej i typ VI ₀ ( n ⁽¹⁾ =1, n ⁽²⁾ =–1, n ⁽³⁾ =0) jest reprezentowany przez czwartą ćwiartkę tej płaszczyzny; typ II (( n ⁽¹⁾ =1, n ⁽²⁾ =0, n ⁽³⁾ =0) jest reprezentowany przez przedział [0,1] wzdłuż n ⁽¹⁾ , a typ I ( n ⁽¹⁾ =0, n ⁽²⁾ =0, n ⁽³⁾ =0) jest na początku. Podobnie w przypadku klasy B (gdzie n ⁽³⁾ = 0), Bianchi typ VI _h ( a = h , n ⁽¹⁾ =1, n ⁽²⁾ =–1) rzutuje na czwartą ćwiartkę płaszczyzny poziomej i typ VII _h ( a = h , n ⁽¹⁾ =1, n ⁽²⁾ =1) rzutuje na pierwszą ćwiartkę płaszczyzny poziomej; te dwa ostatnie typy to pojedyncza klasa izomorfizmu odpowiadająca powierzchni o stałej wartości funkcji h = a ² ( n ⁽¹⁾ n ⁽²⁾ ) ⁻¹ . Typowa taka powierzchnia jest zilustrowana w jednym oktancie, kąt θ określony przez tan θ = | h /2| ^1/2 ; te w pozostałych oktantach uzyskuje się przez obrót o wielokrotności π /2, h zmieniając znak dla danej wielkości | godzina |. Typ III jest podtypem VI _h z a = 1. Typ V ( a =1, n ⁽¹⁾ =0, n ⁽²⁾ =0) to przedział (0,1] wzdłuż osi a i typ IV ( a =1, n ⁽¹⁾ =1, n ^{( 2)} =0) jest pionową otwartą powierzchnią między pierwszą a czwartą ćwiartką płaszczyzny a = 0, przy czym ta ostatnia określa granicę klasy A każdego typu.

Równania Einsteina dla wszechświata o przestrzeni jednorodnej można sprowadzić do układu równań różniczkowych zwyczajnych zawierających tylko funkcje czasu za pomocą pola ramowego. Aby to zrobić, należy rozwiązać składowe przestrzenne czterech wektorów i czterech tensorów wzdłuż triady wektorów bazowych przestrzeni:

${\ Displaystyle R_ {(a) (b)} = R _ {\ alfa \ beta} e_ {(a)} ^ {\ alfa} e_ {(b)} ^ {\ beta}, \ quad R_ {0 (a )}=R_{0\alfa }e_{(a)}^{\alfa},\quad u^{(a)}=u^{\alfa}e_{\alfa}^{(a)},}$

gdzie wszystkie te wielkości są teraz funkcjami samego t ; wielkości skalarne, gęstość energii ε i ciśnienie materii p również są funkcjami czasu.

Równania Einsteina w próżni w synchronicznym układzie odniesienia to

${\ Displaystyle R_ {0} ^ {0} = - {\ Frac {1} {2}} {\ Frac {\ częściowe \varkappa _{\alpha}^{\alpha}}{\częściowe t}}-{\frac {1}{4}}\varkappa _{\alpha}^{\beta}\varkappa _{\beta} ^{\alfa}=0,}$

 

 

 

 

()

${\ Displaystyle R_ {\ alfa} ^ {\ beta} = - {\ Frac {1} {2 {\ sqrt {-g}}}}{\frac {\częściowy }{\częściowy t}}\left({\sqrt {-g}}\varkappa _{\alpha}^{\beta}\right)-P_{ \alfa }^{\beta }=0,}$

 

 

 

 

()

${\ Displaystyle R _ {\ alfa} ^ {0} = {\ Frac {1} {2}} \ lewo (\ varkappa _ { \alpha ;\beta }^{\beta }-\varkappa _{\beta ;\alpha}^{\beta }\right)=0,}$

 

 

 

 

()

gdzie jest trójwymiarowym tensorem $β$${\ Displaystyle \ varkappa _ {\ alfa}$ , a P _αβ to trójwymiarowy tensor Ricciego , który jest wyrażony przez trójwymiarowy tensor metryczny γ _αβ w taki sam sposób jak R _ik wyraża się przez g _ik ; P _αβ zawiera tylko przestrzenne (ale nie czasowe) pochodne γ _αβ . Używając triad, dla równ. 11 jeden ma po prostu

${\ Displaystyle \ varkappa _ {(a) (b)} = {\ Frac {\ częściowe \ eta _ {ab}} {\ częściowe t}}, \ quad \ varkappa _ {(a)} ^ {(b) } = {\ frac {\ częściowy \ eta _ {ac}} {\ częściowy t}} \ eta ^ {cb}.}$

Składowe P _{( a ) ( b )} można wyrazić za pomocą wielkości η _ab i stałych strukturalnych grupy, używając tetradowej reprezentacji tensora Ricciego w kategoriach wielkości ${\ Displaystyle \ lambda _ {abc} = \ lewo (e_ {(a) i, k} -e_ {(a) k, i} \ prawej) e_ {(b)} ^ {i} e_ { (c)}^{k}}$

${\ Displaystyle R_ {(a) (b)} = - {\ Frac {1} {2}} \ lewo (\ lambda _ {ab, c} ^ {c} + \ lambda _ {ba, c} ^ { c}+\lambda _{ca,b}^{c}+\lambda _{cb,a}^{c}+\lambda _{b}^{cd}\lambda _{cda}+\lambda _{ b}^{cd}\lambda _{dca}-{\frac {1}{2}}\lambda _{b}^{cd}\lambda _{acd}+\lambda _{cd}^{c} \lambda _{ab}^{d}+\lambda _{cd}^{c}\lambda _{ba}^{d}\right).}$

Po zastąpieniu symboli z trzema indeksami symbolami z dwoma indeksami C ^ab i przekształceniach: ${\ Displaystyle \ lambda _ {bc} ^ {a} = C_ {bc} ^ {a}}$

${\ Displaystyle \ eta _ {reklama} \ eta _ {bc} \ eta _ {cf} e ^ {def} = \ eta e_ {abc}, \ quad e_ {abf} e ^ {cdf} = \ delta _ { a}^{c}\delta _{b}^{d}-\delta _{a}^{d}\delta _{b}^{c}}$

otrzymuje się „jednorodny” tensor Ricciego wyrażony stałymi struktury:

${\ Displaystyle P_ {(a)} ^ {(b)} = {\ Frac {1} {2 \ eta}} \ lewo \ {2C ^ {bd} C_ {reklama} + C ^ {db} C_ {reklama }+C^{bd}C_{da}-C_{d}^{d}\left(C_{a}^{b}+C_{a}^{b}\right)+\delta _{a} ^{b}\lewo[\lewo(C_{d}^{d}\prawo)^{2}-2C^{df}C_{df}\prawo]\prawo\}.}$

Tutaj wszystkie indeksy są podnoszone i obniżane z lokalnym tensorem metrycznym η _ab

${\ Displaystyle C_ {a} ^ {b} = \ eta _ {ac} C ^ {cb}, \ quad C_ {ab} = \ eta _ {ac} \ eta _ {bd} C ^ {cd}.}$

Tożsamości Bianchiego dla trójwymiarowego tensora P _αβ w przestrzeni jednorodnej przyjmują postać

${\ Displaystyle P_ {b} ^ {c} C_ {ca} ^ {b} + P_ {a} ^ {c} C_ {$

Uwzględnienie przekształceń pochodnych kowariantnych dla dowolnych czterowektorów A _i oraz czterotensorów A _ik

${\ Displaystyle A_ {i; k} e_ {(a)} ^ {i} e_ { (b)}^{k}=A_{(a)(b)}-A^{(d)}\gamma _{dab},}$

${\ Displaystyle A_ {ik; l }e_{(a)}^{i}e_{(b)}^{k}e_{(c)}^{l}=A_{(a)(b)(c)}-A_{(b) }^{(d)}\gamma _{dac}+A_{(a)}^{(d)}\gamma _{dbc},}$

końcowe wyrażenia dla składowych triady czterotensora Ricciego to:

${\ Displaystyle R_ {0} ^ {0} = - {\ Frac { 1}{2}}{\frac {\częściowa \varkappa _{(a)}^{(a)}}{\częściowa t}}-{\frac {1}{4}}\varkappa _{(a )}^{(b)}\varkappa _{(b)}^{(a)},}$

 

 

 

 

()

${\ Displaystyle R_ {(a)} ^ {(b)} = -{\frac {1}{2{\sqrt {\eta}}}}{\frac {\częściowy}}{\częściowy t}}\left({\sqrt {\eta}}\varkappa _{(a) }^{(b)}\right)-P_{(a)}^{(b)},}$

 

 

 

 

()

${\ Displaystyle R_ {(a)} ^ {0} = - {\ Frac {1} {2}} \ varkappa _ {(b)} ^ {(c)} \ lewo (C_ {ca} ^ {b} -\delta _{a}^{b}C_{dc}^{d}\right).}$

 

 

 

 

()

Przy ustalaniu równań Einsteina nie ma zatem potrzeby używania jawnych wyrażeń dla wektorów bazowych jako funkcji współrzędnych.

Zobacz też

• Tabela grup kłamstw
• Lista prostych grup Liego
• Osobliwość BKL

Bibliografia

• Bieliński, Władimir A .; Chałatnikow, IM ; Lifszyc, EM (1971). „Oscylacyjny tryb podejścia do osobliwości w jednorodnych modelach kosmologicznych z obracającymi się osiami”. JETP . 60 (6): 1969–1979.
• Bieliński, Władimir A .; Chałatnikow, IM ; Lifszyc, EM (1972). „Konstrukcja ogólnego kosmologicznego rozwiązania równania Einsteina z osobliwością czasową”. JETP . 62 (5): 1606-1613.
• L. Bianchi, Sugli spazi w trzech wymiarach che ammettono un gruppo continuo di movimenti. (O przestrzeniach trójwymiarowych, które dopuszczają ciągłą grupę ruchów.) Soc. włoski. nauka pam. di Mat. 11, 267 (1898) Tłumaczenie angielskie Zarchiwizowane 2020-02-18 w Wayback Machine
•    Kornwalijski, New Jersey; Levin, JJ (1997a). „Wszechświat Mixmaster jest jednoznacznie chaotyczny” . W Piranie, Tsvi; Ruffini, Remo (red.). O najnowszych osiągnięciach w zakresie teoretycznej i eksperymentalnej ogólnej teorii względności, grawitacji i relatywistycznych teorii pola . Materiały z ósmego spotkania Marcela Grossmana. Uniwersytet Hebrajski w Jerozolimie: World Scientific. s. 616–618. ISBN 978-9810237936 . OL 13168102M .
•    Kornwalijski, Neil J.; Levin, Janna J. (1997b). „Wszechświat Mixmaster jest chaotyczny” . Listy z przeglądu fizycznego . 78 (6): 998–1001. arXiv : gr-qc/9605029 . Bibcode : 1997PhRvL..78..998C . doi : 10.1103/physrevlett.78.998 . ISSN 0031-9007 . S2CID 119476182 .
•    Kornwalijski, Neil J.; Levin, Janna J. (1997c). „Wszechświat Mixmaster: chaotyczna opowieść o Farey” . Przegląd fizyczny D. Amerykańskie Towarzystwo Fizyczne (APS). 55 (12): 7489–7510. arXiv : gr-qc/9612066 . Bibcode : 1997PhRvD..55.7489C . doi : 10.1103/physrevd.55.7489 . ISSN 0556-2821 . S2CID 17085583 .
•   Ferrando, JJ; Saez, JA (2020). „Jednorodne trójwymiarowe przestrzenie Riemanna”. Grawitacja klasyczna i kwantowa . 37 (18): 185011. arXiv : 2004.01877 . Bibcode : 2020CQGra..37r5011F . doi : 10.1088/1361-6382/ab9880 . S2CID 214802205 .
• Guido Fubini Sugli spazi a quattro Dimensioni che ammettono un gruppo continuo di movimenti , (O przestrzeniach czterech wymiarów, które dopuszczają ciągłą grupę ruchów). Ann. Mata. pura appli. (3) 9, 33-90 (1904); przedrukowany w Opere Scelte , a cura dell'Unione matematica italiana e col contributo del Consiglio nazionale delle ricerche, Roma Edizioni Cremonese, 1957–62
•   MacCallum, O klasyfikacji rzeczywistych czterowymiarowych algebr Liego , w „Na ścieżce Einsteina: eseje na cześć Engelberta Schuckinga” pod redakcją AL Harvey, Springer ISBN 0-387-98564-6
•    Henneaux, Marc ; Persson, Daniel; Spindel, Philippe (2008). „Przestrzenne osobliwości i ukryte symetrie grawitacji” . Żywe recenzje w teorii względności . 11 (1): 1. arXiv : 0710.1818 . Bibcode : 2008LRR....11....1H . doi : 10.12942/lrr-2008-1 . PMC 5255974 . PMID 28179821 .
•    Henneaux, Marc ; Persson, Daniel; Wesley, Daniel (2008). „Struktura grupy Coxetera kosmologicznego bilarda na zwartych rozmaitościach przestrzennych”. Journal of High Energy Physics . 2008 (9): 052. arXiv : 0805.3793 . Bibcode : 2008JHEP...09..052H . doi : 10.1088/1126-6708/2008/09/052 . ISSN 1029-8479 . S2CID 14135098 .
•    Henneaux, Marc (2009). „Algebry Kaca-Moody'ego i struktura osobliwości kosmologicznych: nowe światło na analizę Bielińskiego-Khalatnikova-Lifshitza”. Mechanika kwantowa systemów podstawowych: poszukiwanie piękna i prostoty : 1–11. ar Xiv : 0806.4670 . doi : 10.1007/978-0-387-87499-9_11 . ISBN 978-0-387-87498-2 . S2CID 18809715 .
• Robert T. Jantzen, Klasyfikacja 3-geometrii Bianchiego: prace oryginalne w tłumaczeniu
• Jantzen, Robert T. (2001). „Przestrzennie jednorodna dynamika: jednolity obraz”. proc. Int. SCH. fizyka Kurs "E. Fermiego" . LXXXVI . arXiv : gr-qc/0102035 .
•   Landau, Lew D .; Lifszyc, Jewgienij M. (1988). Klasyczna teoria pól (wyd. 7). Moskwa: Nauka . ISBN 978-5-02-014420-0 . Tom. 2 Kursu Fizyki Teoretycznej
• Lifszyc, Jewgienij M .; Chałatnikow, Isaak M. (1963). „Проблемы релятивистской космологии” . Uspekhi Fizicheskikh Nauk . 80 (7): 391–438. doi : 10.3367/UFNr.0080.196307d.0391 . ; Tłumaczenie na język angielski w Lifshitz, EM; Chałatnikow, IM (1963). „Problemy kosmologii relatywistycznej”. Postępy w fizyce . 12 (46): 185. Bibcode : 1963AdPhy..12..185L . doi : 10.1080/00018736300101283 .
•   Ryan, Michael P.; Shepley, Lawrence C. (1975). Homogeniczne kosmologie relatywistyczne . Seria Princeton w fizyce. Princeton, New Jersey: Princeton University Press. ISBN 9780691645209 .
•   Stefani, Hans; Kramer, Dietrich; MacCallum, Malcolm; Hoenselaers, Korneliusz; Herlt, Eduard (2003). Dokładne rozwiązania równań pola Einsteina (wyd. Drugie). Wydawnictwo Uniwersytetu Cambridge. ISBN 978-0-521-46136-8 .
•   Wald, Robert M. (1984). ogólna teoria względności . Chicago: University of Chicago Press. ISBN 0-226-87033-2 .