Notacja wektorowa

Notacja wektorowa

Strzałka wektorowa skierowana od A do B

Składowe wektora Opisanie wektora strzałkowego v za pomocą jego współrzędnych x i y daje izomorfizm przestrzeni wektorowych.

Iloczyn skalarny Dwie równej długości sekwencje wektorów współrzędnych i zwraca pojedynczą liczbę

Iloczyn wektorowy Iloczyn krzyżowy w odniesieniu do prawoskrętnego układu współrzędnych

W matematyce i fizyce notacja wektorowa jest powszechnie stosowaną notacją do reprezentowania wektorów , które mogą być wektorami euklidesowymi lub, bardziej ogólnie, członkami przestrzeni wektorowej .

Do reprezentowania wektora powszechną konwencją typograficzną są małe litery, pionowa pogrubiona czcionka, jak w v . Międzynarodowa Organizacja Normalizacyjna (ISO) zaleca pogrubioną kursywę szeryfową, jak w v , lub szeryfową kursywę bez pogrubienia z akcentem strzałki w prawo, jak w ${\ displaystyle {\ vec {v}}}$ .

W zaawansowanej matematyce wektory są często przedstawiane prostą kursywą, jak każda zmienna .

Historia

W 1835 roku Giusto Bellavitis $,$ ideę równorzędnych skierowanych odcinków linii koncepcją wektora jako takich odcinków.

Termin wektor został ukuty przez WR Hamiltona około 1843 roku, kiedy ujawnił kwaterniony , system, który wykorzystuje wektory i skalary do rozpięcia czterowymiarowej przestrzeni. Dla kwaternionu q = a + b i + c j + d k Hamilton użył dwóch rzutów: S q = a , dla części skalarnej q , oraz V q = b i + c j + d k, część wektora. Używając współczesnych terminów iloczyn krzyżowy (×) i iloczyn skalarny (.), iloczyn kwaternionów dwóch wektorów p i q można zapisać pq = – p . q + p × q . W 1878 roku WK Clifford oddzielił te dwa produkty, aby operacja kwaternionów była użyteczna dla studentów w swoim podręczniku Elements of Dynamic . Wykładowca na Uniwersytecie Yale , Josiah Willard Gibbs dostarczył notację dla iloczynu skalarnego i iloczynu wektorowego , który został wprowadzony w analizie wektorowej .

W 1891 roku Oliver Heaviside przekonywał Clarendona do odróżnienia wektorów od skalarów. Skrytykował użycie greckich liter przez Taita i gotyckich przez Maxwella .

W 1912 roku JB Shaw wniósł swoją „Notację porównawczą dla wyrażeń wektorowych” do Biuletynu Towarzystwa Quaternion . Następnie Alexander Macfarlane opisał w tej samej publikacji 15 kryteriów wyraźnej ekspresji z wektorami.

Idee wektorowe zostały rozwinięte przez Hermanna Grassmanna w 1841 i ponownie w 1862 w języku niemieckim . Ale niemieccy matematycy nie byli tak zachwyceni czwartorzędami, jak anglojęzyczni matematycy. Kiedy Felix Klein organizował niemiecką encyklopedię matematyczną , zlecił Arnoldowi Sommerfeldowi standaryzację notacji wektorowej. W 1950 r., kiedy Academic Press opublikowało przekład G. Kuertiego drugiego wydania tomu 2 Wykładów z fizyki teoretycznej Sommerfelda notacja wektorowa była tematem przypisu: „W oryginalnym tekście niemieckim wektory i ich komponenty są drukowane tymi samymi czcionkami gotyckimi. W tym tłumaczeniu przyjęto bardziej powszechny sposób rozróżniania typograficznego między nimi. "

Wektory prostokątne

Prostokąt

Prostokątny prostopadłościan

Wektor prostokątny to wektor współrzędnych określony przez komponenty definiujące prostokąt (lub prostopadłościan w trzech wymiarach i podobne kształty w większych wymiarach). Punkt początkowy i punkt końcowy wektora leżą na przeciwległych końcach prostokąta (lub pryzmatu itp.).

Uporządkowana notacja zestawu

Prostokątny wektor w $zestawu$ określić za pomocą uporządkowanego komponentów w nawiasy okrągłe lub ostre.

W ogólnym sensie n -wymiarowy wektor v można określić w jednej z następujących postaci:

• ${\ Displaystyle \ mathbf {v} = (v_ {1}, v_ {2}, \ kropki, v_ {n-1}, v_ {N})}$
• ${\ Displaystyle \ mathbf {v} = \ langle v_ {1}, v_ {2}, \ kropki, v_ {n-1}, v_{n}\szereg }$

Gdzie v ₁ , v ₂ , …, v _{n − 1} , v _n są składnikami v .

Notacja macierzowa

Prostokątny wektor w $wierszy lub kolumn$ również określić jako macierz zawierającą uporządkowany zestaw komponentów Wektor określony jako macierz wierszy jest nazywany wektorem wierszowym ; jeden określony jako macierz kolumnowa jest znany jako wektor kolumnowy .

Ponownie n -wymiarowy wektor można określić w jednej z następujących postaci przy użyciu macierzy: ${\ displaystyle \ mathbf {v}}$

• ${\ Displaystyle \ mathbf {v} = {\ rozpocząć {bmatrix} v_ {1} i v_ { 2}&\cdots &v_{n-1}&v_{n}\end{bmatrix}}={\begin{pmatrix}v_{1}&v_{2}&\cdots &v_{n-1}&v_{n}\ koniec {pmacierz}}}$
• ${\ Displaystyle \ mathbf {v} = {\ rozpocząć {bmatrix} v_ {1} \\ v_{2}\\\vdots \\v_{n-1}\\v_{n}\end{bmatrix}}={\begin{pmatrix}v_{1}\\v_{2}\\\vdots \ \v_{n-1}\\v_{n}\end{pmatrix}}}$

gdzie v ₁ , v ₂ , …, v _{n − 1} , v _n są składnikami v . W niektórych zaawansowanych kontekstach wektor wiersza i kolumny mają różne znaczenia; więcej informacji można znaleźć w artykule kowariancja i kontrawariancja wektorów .

Notacja wektorów jednostkowych

Prostokątny wektor w (lub mniej wymiarów, takich jak gdzie $\ mathbb {R} ^ {3}$ _{z poniżej} zero) ${\ Displaystyle$ } określony jako suma wielokrotności skalarnych składowych wektora z elementami bazy standardowej w R $\ displaystyle \ mathbb {R} ^ {3}}$ . Baza jest reprezentowana przez wektory jednostkowe ${\ Displaystyle {\ boldsymbol {\ kapelusz {\ imath}}} = (1,0,0)}$ , ${\ Displaystyle {\ boldsymbol {\ kapelusz {\ jmath}}} = ( 0,1,0)}$ i ${\ Displaystyle {\ boldsymbol {\ hat {k}}} = (0,0,1)}$ .

Trójwymiarowy wektor można określić w następującej postaci, używając notacji wektora jednostkowego: ${\ displaystyle {\ boldsymbol {v}}}$

$${\ Displaystyle \ mathbf {v} = v_ {x} {\ boldsymbol {\ kapelusz {\ imat}}} + v_ {y} {\ boldsymbol { \hat {\jmath}}}+v_{z}{\boldsymbol {\hat {k}}}}$$

Gdzie v _x , v _y i v _z są skalarnymi składnikami v . Składniki skalarne mogą być dodatnie lub ujemne; bezwzględną wartością składnika skalarnego jest jego wielkość.

Wektory biegunowe

Nie należy mylić z wektorem biegunowym , prawdziwym wektorem, w kontekście, w którym rozważane są pseudowektory lub wektory osiowe.

Punkty w biegunowym układzie współrzędnych z biegunem O i osią biegunową L . Na zielono punkt o współrzędnej promieniowej 3 i współrzędnej kątowej 60 stopni, czyli (3,60°). Na niebiesko punkt (4210°).

Dwie współrzędne biegunowe punktu na płaszczyźnie można uznać za wektor dwuwymiarowy. Taki wektor biegunowy składa się z wielkości (lub długości) i kierunku (lub kąta). Wielkość, zwykle przedstawiana jako r , to odległość od punktu początkowego, pochodzenia , do punktu, który jest reprezentowany. Kąt, zwykle przedstawiany jako θ ( grecka litera theta ), to kąt, zwykle mierzony przeciwnie do ruchu wskazówek zegara, między ustalonym kierunkiem, zazwyczaj dodatnim x -oś i kierunek od początku do punktu. Kąt $Displaystyle 0 \$ zwykle zmniejszany tak, aby mieścił się w zakresie lub $}$$\ theta <360 ^ {\ circ$ .

Należy podkreślić, że wektor biegunowy nie jest tak naprawdę wektorem , ponieważ dodanie dwóch wektorów biegunowych nie jest zdefiniowane.

Uporządkowane notacje zbiorcze i macierzowe

Wektory biegunowe można określić za pomocą notacji uporządkowanej pary (podzbiór uporządkowanej notacji zbioru używającej tylko dwóch składowych) lub notacji macierzowej, tak jak w przypadku wektorów prostokątnych. W tych formach pierwszą składową wektora jest r (zamiast v ₁ ), a drugą składową jest θ (zamiast v ₂ ). Aby odróżnić wektory biegunowe od wektorów prostokątnych, kąt można poprzedzić symbolem kąta ${\ displaystyle \ kąt}$ .

Dwuwymiarowy wektor biegunowy v można przedstawić jako dowolny z poniższych, używając uporządkowanej pary lub notacji macierzowej:

• ${\ Displaystyle \ mathbf {v} = (r, \ kąt \ teta)}$
• ${\ Displaystyle \ mathbf {v} = \ langle r, \ kąt \ teta \ rangle}$
• ${\ Displaystyle \ mathbf {v} = {\ rozpocząć {bmatrix} r & \ kąt \ teta \ koniec {bmatrix}}}$
• ${\ Displaystyle \ mathbf {v} = {\ rozpocząć {bmatrix} r \\\ kąt \ theta \ koniec {bmatrix}}}$

gdzie r to wielkość, θ to kąt, a symbol kąta ( $)$ jest opcjonalny

Notacja bezpośrednia

Wektory biegunowe można również określić za pomocą uproszczonych równań autonomicznych, które jawnie definiują r i θ . Może to być nieporęczne, ale jest przydatne, aby uniknąć pomyłki z dwuwymiarowymi prostokątnymi wektorami, która wynika z używania uporządkowanej pary lub notacji macierzowej.

Dwuwymiarowy wektor, którego wielkość wynosi 5 jednostek i którego kierunek wynosi π /9 radianów (20°), można określić za pomocą jednej z następujących postaci:

• ${\ Displaystyle R = 5, \ \ teta = {\ pi \ ponad 9}}$
• ${\ Displaystyle R = 5, \ \ teta = 20 ^ {\ circ}}$

Wektory cylindryczne

Cylindryczny układ współrzędnych o początku O , osi biegunowej A i osi podłużnej L . Kropka to punkt o odległości promieniowej ρ = 4, współrzędnej kątowej φ = 130° i wysokości z = 4.

Wektor cylindryczny jest rozszerzeniem koncepcji wektorów biegunowych na trzy wymiary. Przypomina strzałkę w cylindrycznym układzie współrzędnych . Wektor cylindryczny jest określony przez odległość w xy , kąt i odległość od płaszczyzny xy (wysokość). Pierwsza odległość, zwykle przedstawiana jako r lub ρ (grecka litera rho ), to wielkość rzutu wektora na płaszczyznę xy . Kąt, zwykle przedstawiany jako θ lub φ (grecka litera phi ) jest mierzona jako przesunięcie od linii współliniowej z osią x w kierunku dodatnim; kąt jest zwykle zmniejszany tak, aby mieścił się w zakresie ${\ Displaystyle 0 \ równoważnik \ theta <2 \ pi}$ . Druga odległość, zwykle przedstawiana jako h lub z , to odległość od płaszczyzny xy do punktu końcowego wektora.

Uporządkowane notacje zbiorcze i macierzowe

Wektory cylindryczne są określane podobnie jak wektory biegunowe, w których drugi składnik odległości jest łączony jako trzeci składnik, tworząc uporządkowane trójki (ponownie podzbiór uporządkowanej notacji zbioru) i macierze. Kąt może być poprzedzony symbolem kąta ( ${\ displaystyle \ kąt}$ ); kombinacja odległość-kąt-odległość odróżnia wektory cylindryczne w tym zapisie od wektorów sferycznych w podobnym zapisie.

Trójwymiarowy cylindryczny wektor v można przedstawić jako dowolny z poniższych, używając uporządkowanej trójki lub notacji macierzowej:

• ${\ Displaystyle \ mathbf {v} = (r, \ kąt \ teta, h)}$
• ${\ Displaystyle \ mathbf {v} = \ langle r, \ kąt \ teta, h \ rangle}$
• ${\ Displaystyle \ mathbf {v} = {\ rozpocząć {bmatrix} r & \ kąt \ theta & h \ koniec {bmatrix}}}$
• ${\ Displaystyle \ mathbf {v} = {\ rozpocząć {bmatrix} r \\\ kąt \ theta \\ h \ koniec {bmatrix}}}$

Gdzie r jest wielkością rzutu v na płaszczyznę xy , θ jest kątem między dodatnią osią x a v , a h jest wysokością od płaszczyzny xy do punktu końcowego v . Ponownie symbol kąta ( $jest$ opcjonalny.

Notacja bezpośrednia

Wektor cylindryczny można również określić bezpośrednio, używając uproszczonych równań autonomicznych, które definiują r (lub ρ ), θ (lub φ ) i h (lub z ). Podczas wybierania nazw zmiennych należy zachować spójność; ρ nie należy mieszać z θ i tak dalej.

Trójwymiarowy wektor, którego wielkość rzutu na płaszczyznę xy wynosi 5 jednostek, którego kąt od dodatniej osi x wynosi π /9 radianów (20°) i którego wysokość od płaszczyzny xy wynosi 3 jednostki, może być określone w jednej z następujących form:

• ${\ Displaystyle r = 5, \ \ teta = {\ pi \ ponad 9}, \ h = 3}$
• ${\ Displaystyle r = 5, \ \ teta = 20 ^ {\ circ}, \ h = 3}$
• ${\ Displaystyle \ rho = 5, \ \ phi = {\ pi \ ponad 9}, \ z = 3}$
• ${\ Displaystyle \ rho = 5, \ \ phi = 20 ^ {\ circ}, \ z = 3}$

Wektory sferyczne

Współrzędne sferyczne ( r , θ , φ ) często używane w matematyce : odległość promieniowa r , kąt azymutalny θ i kąt biegunowy φ . Znaczenia θ i φ zostały zamienione w porównaniu z konwencją fizyki.

Wektor sferyczny to kolejna metoda rozszerzania koncepcji wektorów biegunowych na trzy wymiary. Przypomina to strzałkę w sferycznym układzie współrzędnych . Wektor sferyczny jest określony przez wielkość, kąt azymutu i kąt zenitu. Wielkość jest zwykle przedstawiana jako ρ . Kąt azymutu, zwykle przedstawiany jako θ , jest przesunięciem (w kierunku przeciwnym do ruchu wskazówek zegara) od dodatniej osi x . Kąt zenitalny, zwykle przedstawiany jako φ , jest przesunięciem od dodatniego z -oś. Oba kąty są zwykle redukowane tak, aby mieściły się w zakresie od zera (włącznie) do 2 π (wyłącznie).

Uporządkowane notacje zbiorcze i macierzowe

Wektory sferyczne są określane podobnie jak wektory biegunowe, w których kąt zenitalny jest łączony jako trzeci składnik, tworząc uporządkowane trójki i macierze. Kąty azymutu i zenitu mogą być poprzedzone symbolem kąta ( ${\ displaystyle \ kąt}$ ); przedrostek powinien być używany konsekwentnie, aby utworzyć kombinację odległość-kąt-kąt, która odróżnia wektory sferyczne od wektorów cylindrycznych.

Trójwymiarowy sferyczny wektor v można przedstawić jako dowolny z poniższych, używając uporządkowanej trójki lub notacji macierzowej:

• ${\ Displaystyle \ mathbf {v} = (\ rho, \ kąt \ teta, \ kąt \ phi)}$
• ${\ Displaystyle \ mathbf {v} = \ langle \ rho \ kąt \ teta \ kąt \ phi \ rangle}$
• ${\ Displaystyle \ mathbf {v} = {\ rozpocząć {bmatrix} \ rho & \ kąt \ theta & \ kąt \ phi \ koniec {bmatrix}}}$
• ${\ Displaystyle \ mathbf {v} = {\ rozpocząć {bmatrix} \ rho \\\ kąt \ theta \\\ kąt \ phi \ koniec {bmatrix}}}$

Gdzie ρ to wielkość, θ to kąt azymutu, a φ to kąt zenitalny.

Notacja bezpośrednia

Podobnie jak wektory biegunowe i cylindryczne, wektory sferyczne można określić za pomocą uproszczonych równań autonomicznych, w tym przypadku dla ρ , θ i φ .

Trójwymiarowy wektor, którego wielkość wynosi 5 jednostek, którego kąt azymutu wynosi π /9 radianów (20°), a kąt zenitalny wynosi π /4 radianów (45°), można określić jako:

• ${\ Displaystyle \ rho = 5, \ \ teta = {\ pi \ ponad 9}, \ \ phi = {\ pi \ ponad 4}}$
• ${\ Displaystyle \ rho = 5, \ \ teta = 20 ^ {\ circ}, \ \ phi = 45 ^ {\ circ}}$

Operacje

W dowolnej przestrzeni wektorowej zdefiniowane są operacje dodawania wektorów i mnożenia przez skalar. Znormalizowane przestrzenie wektorowe definiują również operację znaną jako norma (lub określenie wielkości). Przestrzenie iloczynu wewnętrznego definiują również operację zwaną iloczynem wewnętrznym. W $wewnętrzny jest$ jako iloczyn skalarny . w ${\ Displaystyle \ mathbb {R} ^ {3}}$ i ${\ Displaystyle \ mathbb {R} ^ {7}}$ zdefiniowana jest również dodatkowa operacja znana jako iloczyn krzyżowy .

Dodawanie wektorów

Dodawanie wektorów jest reprezentowane przez znak plus używany jako operator między dwoma wektorami. Suma dwóch wektorów u i v byłaby przedstawiona jako:

$${\ Displaystyle \ mathbf {u} + \ mathbf {v}}$$

Mnożenie przez skalar

Mnożenie przez skalar jest reprezentowane w taki sam sposób jak mnożenie algebraiczne. Skalar obok wektora (jeden lub oba mogą być w nawiasach) implikuje mnożenie przez skalar. Dwa wspólne operatory, kropka i obrócony krzyż, są również dopuszczalne (chociaż obrócony krzyżyk prawie nigdy nie jest używany), ale ryzykują pomyłkę z iloczynami skalarnymi i iloczynami krzyżowymi, które działają na dwóch wektorach. Iloczyn skalara k z wektorem v można przedstawić w dowolny z następujących sposobów:

• ${\ displaystyle k \ mathbf {v}}$
• ${\ Displaystyle k \ cdot \ mathbf {v}}$

Odejmowanie i dzielenie wektorów przez skale

Korzystając z algebraicznych właściwości odejmowania i dzielenia, wraz z mnożeniem przez skalar, możliwe jest również „odjęcie” dwóch wektorów i „podzielenie” wektora przez skalar.

Odejmowanie wektorów jest wykonywane przez dodanie skalarnej wielokrotności -1 z drugim operandem wektora do pierwszego operandu wektora. Można to przedstawić za pomocą znaku minus jako operatora. Różnicę między dwoma wektorami u i v można przedstawić w jeden z następujących sposobów:

• ${\ Displaystyle \ mathbf {u} + - \ mathbf {v}}$
• ${\ Displaystyle \ mathbf {u} - \ mathbf {v}}$

Dzielenie przez skalar jest wykonywane przez pomnożenie operandu wektora przez numeryczną odwrotność operandu skalarnego. Można to przedstawić za pomocą kreski ułamkowej lub znaków podziału jako operatorów. Iloraz wektora v i skalara c można przedstawić w dowolnej z następujących postaci:

• ${\ Displaystyle {1 \ ponad c} \ mathbf {v}}$
• ${\ Displaystyle {\ mathbf {v} \ ponad c}}$
• ${\ Displaystyle {\ mathbf {v} \ div c}}$

Norma

Norma wektora jest reprezentowana przez podwójne kreski po obu stronach wektora. Normę wektora v można przedstawić jako:

$${\ Displaystyle \|\ mathbf {v} \|}$$

Norma jest również czasami przedstawiana za pomocą pojedynczych słupków, na przykład ${\ displaystyle |\ mathbf {v} |}$ , ale można to pomylić z wartością bezwzględną (która jest rodzajem normy).

Produkt wewnętrzny

Iloczyn wewnętrzny dwóch wektorów (znany również jako iloczyn skalarny, którego nie należy mylić z mnożeniem przez skalar) jest reprezentowany jako uporządkowana para ujęta w nawiasy ostre. Iloczyn wewnętrzny dwóch wektorów u i v byłby przedstawiony jako:

$${\ Displaystyle \ langle \ mathbf {u} \ mathbf {v} \ rangle}$$

Produkt w kropki

W $wewnętrzny jest również$ jako iloczyn skalarny . Oprócz standardowej notacji iloczynu wewnętrznego można również użyć notacji iloczynu skalarnego (z użyciem kropki jako operatora) (i jest ona bardziej powszechna). Iloczyn skalarny dwóch wektorów u i v można przedstawić jako:

$${\ Displaystyle \ mathbf {u} \ cdot \ mathbf {v}}$$

W niektórych starszych literaturach iloczyn skalarny jest implikowany między dwoma wektorami zapisanymi obok siebie. Ten zapis można pomylić z iloczynem diadycznym między dwoma wektorami.

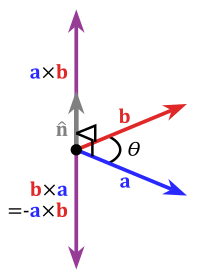
Produkt krzyżowy

Iloczyn krzyżowy dwóch wektorów ( $w$ operatora. Iloczyn krzyżowy dwóch wektorów u i v byłby przedstawiony jako:

$${\ Displaystyle \ mathbf {u} \ razy \ mathbf {v}}$$

W niektórych konwencjach (np. we Francji iw niektórych obszarach matematyki wyższej) jest to również oznaczane klinem, co pozwala uniknąć pomylenia z iloczynem klina, ponieważ oba są funkcjonalnie równoważne w trzech wymiarach:

$${\ Displaystyle \ mathbf {u} \ klin \ mathbf {v}}$$

u i v stosuje się następującą notację :

$${\ Displaystyle [\ mathbf {u} \ mathbf {v} ]}$$

Nabla

Główne artykuły: symbol Del i Nabla

Notacja wektorowa jest używana z rachunkiem różniczkowym za pośrednictwem operatora Nabla :

$${\ Displaystyle \ mathbf {i} {\ Frac {\ częściowy} {\ częściowy x}} + \ mathbf {j} {\ Frac {\ częściowy}} {\ częściowe y}}+\mathbf {k} {\frac {\częściowe }{\częściowe z}}}$$

W przypadku funkcji skalarnej f gradient jest zapisywany jako $\ Displaystyle \ nabla f \,,}$ {

z polem wektorowym F rozbieżność jest zapisywana jako ${\ Displaystyle \ nabla \ cdot F,$ }

a przy polu wektorowym F zwijanie jest zapisywane jako ${\ Displaystyle \ nabla \ razy F.}$

Zobacz też

• Wektor euklidesowy
• ISO 31-11 § Wektory i tensory
• Fazor