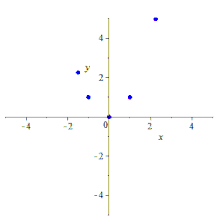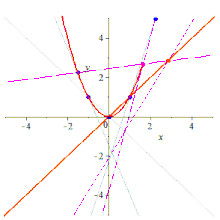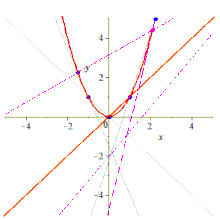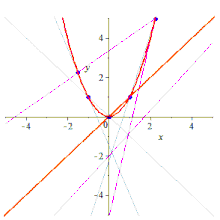
Pięć punktów określa stożek

W geometrii euklidesowej i rzutowej pięć punktów określa stożek ( krzywą płaską stopnia 2), tak jak dwa (odrębne) punkty wyznaczają linię ( krzywą płaską stopnia 1 ). Istnieją dodatkowe subtelności dla stożków , które nie istnieją dla linii, a zatem stwierdzenie i jego dowód dla stożków są bardziej techniczne niż dla linii.

Formalnie, biorąc pod uwagę dowolne pięć punktów na płaszczyźnie w ogólnym położeniu liniowym , co oznacza, że ​​nie ma trzech współliniowych , przechodzi przez nie unikalny stożek, który nie będzie zdegenerowany ; dotyczy to zarówno płaszczyzny euklidesowej , jak i dowolnej płaszczyzny rzutowej Pappiana . Rzeczywiście, biorąc pod uwagę dowolne pięć punktów, przechodzi przez nie stożek, ale jeśli trzy z tych punktów są współliniowe, stożek będzie zdegenerowany (redukowalny, ponieważ zawiera linię) i może nie być unikalny; zobacz dalszą dyskusję .

Dowody

Wynik ten można udowodnić na wiele różnych sposobów; argument dotyczący liczenia wymiarów jest najbardziej bezpośredni i uogólnia się w większym stopniu, podczas gdy inne dowody są szczególne dla stożków.

Liczenie wymiarów

Intuicyjnie przejście przez pięć punktów w ogólnej pozycji liniowej określa pięć niezależnych ograniczeń liniowych na (rzutowej) liniowej przestrzeni stożków, a tym samym określa unikalny stożek, chociaż to krótkie stwierdzenie ignoruje subtelności.

Dokładniej, wygląda to następująco:

• stożki odpowiadają punktom w pięciowymiarowej przestrzeni rzutowej ${\ Displaystyle \ mathbf {P} ^ {5};}$
• $y$${\ Displaystyle Ax ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0}$ współrzędne: równania jest równaniem liniowym w ${\ Displaystyle (A, B, C, D, E, F);}$
• przez liczenie wymiarów , pięć ograniczeń (że krzywa przechodzi przez pięć punktów) jest potrzebnych do określenia stożka, ponieważ każde ograniczenie zmniejsza wymiar możliwości o 1, a jedno zaczyna się od 5 wymiarów;
• w 5 wymiarach przecięcie 5 (niezależnych) hiperpłaszczyzn jest pojedynczym punktem (formalnie, na mocy twierdzenia Bézouta );
• ogólne liniowe położenie punktów oznacza, że ​​więzy są niezależne, a zatem określają unikalny stożek;
• wynikowy stożek nie jest zdegenerowany, ponieważ jest krzywą (ponieważ ma więcej niż 1 punkt) i nie zawiera linii (w przeciwnym razie podzieliłby się na dwie linie, z których przynajmniej jedna musi zawierać 3 z 5 punktów, przez zasadę przegródki ), więc jest nieredukowalna.

Dwie subtelności w powyższej analizie polegają na tym, że wynikowy punkt jest równaniem kwadratowym (nie równaniem liniowym) oraz że ograniczenia są niezależne. Pierwszy jest prosty: jeśli $,$ , B i C znikają równanie linię i dowolne 3 punkty na niej liczba punktów) leżą na linii – w ten sposób ogólne położenie liniowe zapewnia stożek. Drugie, że ograniczenia są niezależne, jest znacznie subtelniejsze : odpowiada faktowi, że biorąc pod uwagę pięć punktów w ogólnym położeniu liniowym na płaszczyźnie, ich obrazy w ${\ displaystyle \ mathbf {P} ^ {5}}$ Mapa Veronese'a jest generalnie liniowa, co jest prawdą, ponieważ mapa Veronese'a jest dwuregularna : tzn. jeśli obraz pięciu punktów spełnia zależność, to zależność może zostać cofnięta, a oryginalne punkty również muszą spełniać zależność. Mapa $},$$_ 2}$$D: E: F]}$ cel jest podwójny do $do:$$[A: B: C$ stożków ${\ Displaystyle \ mathbf {P} ^ {5}} .$ Mapa Veronese odpowiada „ocenie stożka w punkcie”, a stwierdzenie o niezależności ograniczeń jest właśnie stwierdzeniem geometrycznym dotyczącym tej mapy.

Syntetyczny dowód

To, że pięć punktów określa stożek, można udowodnić za pomocą geometrii syntetycznej — tj. w kategoriach linii i punktów na płaszczyźnie — oprócz dowodu analitycznego (algebraicznego) podanego powyżej. Dowód taki można przeprowadzić za pomocą twierdzenia Jakoba Steinera , które stwierdza:

Biorąc pod uwagę przekształcenie rzutowe f , między ołówkiem linii przechodzących przez punkt X a ołówkiem linii przechodzących przez punkt Y, zbiór C punktów przecięcia między linią x a jej obrazem ${\ displaystyle f (x )}$ tworzy stożek.

Zauważ, że X i Y leżą na tym stożku, biorąc pod uwagę preobraz i obraz linii XY (która jest odpowiednio linią przechodzącą przez X i linią przechodzącą przez Y ).

$1: 0$ pokazać, biorąc punkty X i Y do punktów standardowych i $\ Displaystyle [0$ przez transformacja rzutowa, w której to przypadku ołówki linii odpowiadają poziomej i pionowej linii na płaszczyźnie, a przecięcia odpowiednich linii wykresowi funkcji, która (musi być pokazana) jest hiperbolą, stąd stożek, stąd pierwotna krzywa C jest stożkiem.

$Displaystyle XA$ pięć punktów X, , trzy linie można przenieść na trzy linie $} \displaystyle YA,YB,YC}$ przez unikalną transformację rzutową, ponieważ transformacje rzutowe są po prostu 3-przechodnie na liniach (są po prostu 3-przechodnie na punktach, stąd dzięki dwoistości rzutowej są 3-przechodnie na liniach). Pod tą mapą X odwzorowuje Y, ponieważ są to unikalne punkty przecięcia tych linii, a zatem spełniają hipotezę twierdzenia Steinera. Powstały stożek zawiera zatem wszystkie pięć punktów i jest unikalnym stożkiem, zgodnie z życzeniem.

Konstrukcja paraboli, biorąc pod uwagę pięć punktów

Budowa

Biorąc pod uwagę pięć punktów, można skonstruować zawierający je stożek na różne sposoby.

Analitycznie, biorąc pod uwagę współrzędne ${\ Displaystyle (x_ {i}, y_ {i}) _ {i = 1,2,3,4,5 }}$ z pięciu punktów równanie stożka można znaleźć za pomocą algebry liniowej , zapisując i rozwiązując pięć równań we współczynnikach, podstawiając zmienne wartościami współrzędnych: pięć równań, sześć niewiadomych, ale jednorodnych, więc skalowanie usuwa jeden wymiar; konkretnie, ustawienie jednego ze współczynników na 1 osiąga to.

Można to osiągnąć całkiem bezpośrednio za pomocą następującego równania wyznacznikowego:

${\ Displaystyle \ det {\ rozpocząć {bmatrix} x ^{2}&xy&y^{2}&x&y&1\\x_{1}^{2}&x_{1}y_{1}&y_{1}^{2}&x_{1}&y_{1}&1\\x_{2 }^{2}&x_{2}y_{2}&y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}&x_{3}y_{3}&y_{ 3}^{2}&x_{3}&y_{3}&1\\x_{4}^{2}&x_{4}y_{4}&y_{4}^{2}&x_{4}&y_{4}&1 \\x_{5}^{2}&x_{5}y_{5}&y_{5}^{2}&x_{5}&y_{5}&1\end{bmacierz}}=0}$

Ta macierz ma zmienne w pierwszym rzędzie i liczby we wszystkich pozostałych wierszach, więc wyznacznik jest widocznie liniową kombinacją sześciu jednomianów stopnia co najwyżej 2. Ponadto wynikowy wielomian wyraźnie znika w pięciu punktach wejściowych (kiedy ${\ Displaystyle (x, y) = (x_ {i}, y_ {i})} )$ , ponieważ macierz ma wtedy powtarzający się wiersz.

Syntetycznie stożek można skonstruować za pomocą konstrukcji Braikenridge'a-Maclaurina , stosując twierdzenie Braikenridge'a-Maclaurina , które jest odwrotnością twierdzenia Pascala . Twierdzenie Pascala mówi, że mając 6 punktów na stożku (sześciokącie), proste wyznaczone przez przeciwległe boki przecinają się w trzech współliniowych punktach. Można to odwrócić, aby skonstruować możliwe lokalizacje dla szóstego punktu, biorąc pod uwagę 5 istniejących.

Uogólnienia

Naturalnym uogólnieniem jest pytanie, dla jakiej wartości k konfiguracja k punktów (w pozycji ogólnej) w n -przestrzeni określa rozmaitość stopnia d i wymiaru m , co jest fundamentalnym pytaniem w geometrii wyliczeniowej .

Prostym tego przykładem jest hiperpowierzchnia $1$ podrozmaitość współwymiaru , wielomianu, przypadek , której przykładem są płaskie krzywe

W przypadku hiperpowierzchni odpowiedź jest podana w postaci współczynnika wielozbiorowego , bardziej znanego współczynnika dwumianowego lub bardziej elegancko rosnącej silni , jako:

${\ Displaystyle k = \ lewo (\! \! {n + 1 \ wybierz d} \! \! \ prawej) -1 = {n + d \ wybierz d} - 1={\frac {1}{n!}}(d+1)^{(n)}-1.}$

Odbywa się to poprzez analogiczną analizę mapy Veronese : k punktów w ogólnej pozycji nakłada k niezależnych warunków liniowych na rozmaitość (ponieważ mapa Veronese jest dwuregularna), a liczba jednomianów stopnia d w ${\ displaystyle n + 1}$ zmienne ( n $)$ przestrzeń rzutowa ma jednorodne współrzędne) jest $textstyle {\ lewo (\! \! {n$ od którego odejmuje się 1 z powodu rzutowania: mnożenie wielomianu przez stałą nie zmienia jego zer.

W powyższym wzorze liczba punktów k jest wielomianem w d stopnia n, z wiodącym współczynnikiem ${\ Displaystyle 1/n!}$

W przypadku krzywych płaskich, gdzie wzór przyjmuje postać: ${\ displaystyle n = 2,}$

${\ Displaystyle \ textstyle {\ Frac {1} {2}} (d + 1) (d + 2) - 1 = \ textstyle {\ frac {1} {2}} (d ^ {2} + 3d)}$

którego wartości dla ${\ Displaystyle d = 0,1,2,3,4}$ to ${\ Displaystyle 0,2,5,9,14}$ – nie ma krzywych stopnia 0 (pojedynczy punkt jest punktem, a więc jest wyznaczony przez punkt, który jest kowymiarem 2), 2 punkty określają prostą, 5 punktów określa stożek, 9 punktów określa sześcienny, 14 punktów określa kwartet i tak dalej.

Powiązane wyniki

Podczas gdy pięć punktów określa stożek, zbiory sześciu lub więcej punktów na stożku nie znajdują się w położeniu ogólnym, to znaczy są ograniczone, jak pokazano w twierdzeniu Pascala .

Podobnie, podczas gdy dziewięć punktów określa sześcienny, jeśli dziewięć punktów leży na więcej niż jednym sześciennym - tj. są one przecięciem dwóch sześciennych - to nie znajdują się one w położeniu ogólnym i rzeczywiście spełniają ograniczenie dodawania, jak stwierdzono w Cayley –Twierdzenie Bacharacha .

Cztery punkty nie określają stożka, ale raczej ołówek , 1-wymiarowy liniowy system stożków , które wszystkie przechodzą przez cztery punkty (formalnie mają cztery punkty jako miejsce bazowe ). Podobnie trzy punkty określają dwuwymiarowy układ liniowy (siatka), dwa punkty określają trójwymiarowy układ liniowy (sieć), jeden punkt określa czterowymiarowy układ liniowy, a punkty zerowe nie nakładają żadnych ograniczeń na pięciowymiarowy układ liniowy system wszystkich stożków.

Koła apollińskie to dwie 1-parametrowe rodziny określone przez 2 punkty.

Jak dobrze wiadomo, trzy niewspółliniowe punkty wyznaczają okrąg w geometrii euklidesowej, a dwa różne punkty wyznaczają ołówek okręgów, takich jak koła apollińskie . Wyniki te wydają się być sprzeczne z ogólnym wynikiem, ponieważ koła są szczególnymi przypadkami stożków. Jednak w płaszczyźnie rzutowej pappiana stożek jest kołem tylko wtedy, gdy przechodzi przez dwa określone punkty na linii w nieskończoności , więc okrąg jest określony przez pięć niewspółliniowych punktów, trzy na płaszczyźnie afinicznej i te dwa punkty specjalne. Podobne względy wyjaśniają mniejszą niż oczekiwano liczbę punktów potrzebnych do zdefiniowania ołówków okręgów.

styczność

Zamiast przechodzić przez punkty, inny warunek na krzywej jest styczny do danej linii. Bycie styczną do pięciu danych linii również określa stożek, przez dwoistość rzutową , ale z algebraicznego punktu widzenia styczność do prostej jest ograniczeniem kwadratowym , więc naiwne liczenie wymiarów daje 2 ^{· 5} = 32 stożki styczne do pięciu danych linii, z czego 31 należy przypisać zdegenerowanym stożkom, jak opisano we współczynnikach fudge w geometrii wyliczeniowej ; sformalizowanie tej intuicji wymaga znacznego dalszego rozwoju, aby uzasadnić.

Innym klasycznym problemem geometrii wyliczeniowej, podobnym do stożkowych, jest problem Apoloniusza : okrąg, który jest styczny do trzech okręgów, ogólnie określa osiem okręgów, ponieważ każdy z nich jest warunkiem kwadratowym i 2 ³ = 8. Jako pytanie w rzeczywistej geometrii pełna analiza obejmuje wiele szczególnych przypadków, a rzeczywista liczba okręgów może być dowolną liczbą z przedziału od 0 do 8, z wyjątkiem 7.

Zobacz też

• Twierdzenie Cramera (krzywe algebraiczne) , dla uogólnienia na krzywe planarne n -tego stopnia

• Coxeter, HSM (1961), Wprowadzenie do geometrii , Waszyngton, DC
• Coxeter, HSM ; Greitzer, SL (1967), Geometry Revisited , Washington, DC: Mathematical Association of America , s. 76
•   Dixon, AC (marzec 1908), „Stożek przez pięć podanych punktów” , The Mathematical Gazette , The Mathematical Association , 4 (70): 228–230, doi : 10,2307/3605147 , JSTOR 3605147

Linki zewnętrzne

• Pięć punktów określa przekrój stożkowy , interaktywna demonstracja Wolfram