Problem maksymalizacji użyteczności

Maksymalizacja użyteczności została po raz pierwszy opracowana przez filozofów utylitaryzmu, Jeremy'ego Benthama i Johna Stuarta Milla . W mikroekonomii problem maksymalizacji użyteczności jest problemem, przed którym stają konsumenci : „Jak mam wydać pieniądze , aby zmaksymalizować użyteczność ?” Jest to rodzaj optymalnego problemu decyzyjnego . Polega na wybraniu, ile każdego dostępnego dobra lub usługi należy skonsumować, biorąc pod uwagę ograniczenie całkowitych wydatków (dochód), ceny towarów i ich preferencje .

Maksymalizacja użyteczności jest ważną koncepcją w teorii konsumentów, ponieważ pokazuje, w jaki sposób konsumenci decydują się na alokację swoich dochodów. Ponieważ konsumenci są racjonalni , starają się wydobyć jak najwięcej korzyści dla siebie. Jednak ze względu na ograniczoną racjonalność i inne uprzedzenia konsumenci czasami wybierają pakiety, które niekoniecznie maksymalizują ich użyteczność. Pakiet maksymalizacji użyteczności konsumenta również nie jest ustalony i może zmieniać się w czasie w zależności od jego indywidualnych preferencji co do towarów, zmian cen oraz wzrostu lub spadku dochodów.

Podstawowe ustawienia

Aby maksymalizować użyteczność, istnieją cztery podstawowe etapy procesu wyznaczania popytu konsumpcyjnego i znajdowania pakietu maksymalizującego użyteczność konsumenta przy danych cenach, dochodach i preferencjach.

1 ) Sprawdź , czy prawo Walrasa jest spełnione

1) Prawo Walrasa

Prawo Walrasa mówi, że jeśli preferencje konsumentów są kompletne, monotonne i przechodnie, to optymalny popyt będzie leżał na linii budżetowej .

Preferencje konsumenta

Aby istniała reprezentacja użyteczności, preferencje konsumenta muszą być kompletne i przechodnie (warunki konieczne).

Kompletny

Kompletność preferencji wskazuje, że wszystkie koszyki w zbiorze konsumpcyjnym mogą być porównywane przez konsumenta. Na przykład, jeśli konsument ma 3 pakiety A, B i C, to;

ZA ${\ Displaystyle \ succcurlyeq}$ b, ZA ${\ Displaystyle \ succcurlyeq} do$ , b ${\ Displaystyle \ succcurlyeq}$ ZA, b ${\ Displaystyle \ succcurlyeq} do$ , do ${\ Displaystyle \ succcurlyeq}$ B, do ${\ Displaystyle \ succcurlyeq}$ ZA, ZA ${\ Displaystyle \ succcurlyeq}$ ZA, b ${\ Displaystyle \ succcurlyeq}$ b, do ${\ Displaystyle \ succcurlyeq}$ C. Konsument ma zatem pełne preferencje, ponieważ może porównać każdy pakiet.

Przechodni

Przechodniość stwierdza, że preferencje jednostek są spójne we wszystkich wiązkach.

$B$ związku z tym, jeśli konsument słabo preferuje A nad B ( $)$ $i$ C oznacza to, że C A jest słabo preferowane do )

Monotonia

Aby relacja preferencji była monotoniczna , zwiększanie ilości obu dóbr powinno poprawiać sytuację konsumenta (zwiększać jego użyteczność), a zwiększanie ilości jednego dobra przy stałej ilości drugiego nie powinno pogarszać sytuacji konsumenta (taka sama użyteczność).

Preferencja jest monotonna $;$ i tylko wtedy, gdy

1) ${\ Displaystyle (x + \ epsilon, y) \ succcurlyeq (x, y)}$

2) ${\ Displaystyle (x, y + \ epsilon) \ succcurlyeq (x, y)}$

3) ${\ Displaystyle (x + \ epsilon, y + \ epsilon) \ succ (x, y)}$

gdzie ${\ Displaystyle \ epsilon}$ > 0

2) „Uderzające pieniądze”

Bang for buck jest główną koncepcją maksymalizacji użyteczności i polega na tym, że konsument chce uzyskać najlepszą wartość za swoje pieniądze. Jeśli prawo Walrasa zostało spełnione, optymalne rozwiązanie konsumenta leży w punkcie przecięcia linii budżetowej i optymalnej krzywej obojętności, co nazywa się warunkiem styczności. Aby znaleźć ten punkt, zróżniczkuj funkcję użyteczności względem x i y, aby znaleźć użyteczności krańcowe, a następnie podziel przez odpowiednie ceny towarów.

${\ Displaystyle MU_ {x} / p_ {x} = MU_ {y} / p_ {y}}$

Można to rozwiązać, aby znaleźć optymalną ilość dobra x lub dobra y.

3) Ograniczenie budżetowe

Podstawowa konfiguracja ograniczenia budżetowego konsumenta jest następująca: ${\ Displaystyle p_ {x} x + p_ {y} y \ równoważnik I}$

Ze względu na spełnienie prawa Walrasa: ${\ displaystyle p_ {x} x + p_ {y} y = ja}$

Warunek styczności jest następnie zastępowany w celu rozwiązania optymalnej ilości drugiego dobra.

4) Sprawdź negatywność

Rysunek 1: Przedstawia miejsce, w którym pakiet maksymalizujący użyteczność znajduje się, gdy popyt na jedno dobro jest ujemny

Należy sprawdzić ujemność, ponieważ problem maksymalizacji użyteczności może dać odpowiedź, w której optymalny popyt na dobro jest ujemny, co w rzeczywistości nie jest możliwe, ponieważ jest to poza dziedziną. Jeśli popyt na jedno dobro jest ujemny, optymalny pakiet konsumpcyjny będzie taki, gdzie 0 tego dobra jest konsumowane, a cały dochód jest wydawany na drugie dobro (rozwiązanie narożnikowe). Zobacz rysunek 1, aby zobaczyć przykład, gdy popyt na dobro x jest ujemny.

Reprezentacja techniczna

zbiór konsumpcyjny konsumenta lub wyliczenie wszystkich możliwych wiązek konsumpcyjnych, które można by wybrać, gdyby istniały ograniczenia budżetowe.

Zbiór konsumpcji = ${\ Displaystyle \ mathbb {R} _ {+} ^ {n} \ .}$ (zbiór dodatnich liczb rzeczywistych, konsument nie może preferować ujemnej ilości towarów).

${\ Displaystyle x \ w \ mathbb {R} _ {+} ^ {n} \ .}$

Załóżmy również, że wektor cen ( p ) n towarów jest dodatni,

Rysunek 2: Pokazuje optymalne ilości dóbr x i y, które maksymalizują użyteczność przy ograniczeniu budżetowym.

${\ Displaystyle p \ w \ mathbb {R} _ {+} ^ {n} \,}$

i że dochód konsumenta wynosi ${\ displaystyle w}$ ; wtedy zestaw wszystkich przystępnych cenowo pakietów, zestaw budżetowy to,

${\ Displaystyle B (p, ja) = \ {x \ w \ mathbb {R} _ {+} ^ {n} | \ mathbb {\ Sigma} _ { i=1}^{n}p_{i}x_{i}\równik I\}\ ,}$

Konsument chciałby kupić najkorzystniejszy cenowo pakiet towarów.

Zakłada się, że konsument ma porządkową funkcję użyteczności , zwaną u . Jest to funkcja o wartościach rzeczywistych, której domeną jest zbiór wszystkich wiązek towarów, lub

{\ Displaystyle u: \ mathbb {R} _ {+} ^ {n} \ rightarrow \ mathbb {R} _ {+} \ .}

$p,w)}$ konsumenta $Displaystyle$ pakiet maksymalizujący użyteczność wszystkich pakietów w zbiorze budżetowym, jeśli $in$ to optymalna funkcja popytu konsumentów to:

${\ Displaystyle x (p, ja) = \ {x \ w B (p, ja) | U (x) \ geq U (y )\forall y\in B(p,I)\}}$

Znalezienie $_$ _ _ _

Jeśli u jest $ciągłe$ i żadne towary nie są bezpłatne, to ale Jeżeli preferencje konsumenta są zupełne, przechodnie i ściśle wypukłe, to popyt konsumenta zawiera jednoznaczny maksymalizator dla wszystkich wartości parametrów cenowych i majątkowych. Jeśli to $nazywa$ spełnione funkcją popytu W przeciwnym razie ${\ Displaystyle x (p, ja)}$ ma wartość ustaloną i nazywa się to marszałkowską korespondencją popytową .

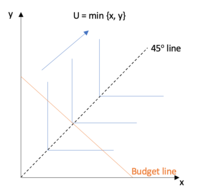
Maksymalizacja użyteczności doskonałych uzupełnień

U = min {x, y}

Rysunek 3: To pokazuje problem maksymalizacji użyteczności z minimalną funkcją użyteczności.

W przypadku funkcji minimalnej z dobrami, które są doskonałymi uzupełnieniami , nie można wykonać tych samych kroków, aby znaleźć pakiet maksymalizujący użyteczność, ponieważ jest to funkcja nieróżniczkowalna. Dlatego należy korzystać z intuicji. Konsument zmaksymalizuje swoją użyteczność w punkcie załamania najwyższej krzywej obojętności, która przecina linię budżetu, gdzie x = y. To intuicja, ponieważ konsument jest racjonalny, nie ma sensu, aby konsument konsumował więcej jednego dobra, a nie drugiego, ponieważ ich użyteczność jest brana na minimum z dwóch (nie mają z tego żadnej korzyści w użyteczności i marnowaliby swoje dochód). Patrz rysunek 3.

Maksymalizacja użyteczności doskonałych substytutów

U = x + y

W przypadku funkcji użyteczności z doskonałymi substytutami pakiet maksymalizujący użyteczność można znaleźć przez zróżnicowanie lub po prostu przez inspekcję. Załóżmy, że konsument słucha australijskich zespołów rockowych AC/DC i Tame Impala doskonałe zamienniki. Oznacza to, że chętnie spędzą całe popołudnie słuchając tylko AC/DC, albo tylko Tame Impala, albo w trzech czwartych AC/DC i w jednej czwartej Tame Impala, albo dowolnej kombinacji tych dwóch pasm w dowolnej ilości. Dlatego o optymalnym wyborze konsumenta decydują wyłącznie względne ceny słuchania obu artystów. Jeśli udział w koncercie Tame Impala jest tańszy niż udział w koncercie AC/DC, konsument wybiera udział w koncercie Tame Impala i odwrotnie. Jeśli ceny dwóch koncertów są takie same, konsument jest całkowicie obojętny i może rzucić monetą, aby zdecydować. Aby zobaczyć to matematycznie, rozróżnij funkcję użyteczności, aby stwierdzić, że MRS jest stała - takie jest techniczne znaczenie doskonałych substytutów. W rezultacie rozwiązanie problemu ograniczonej maksymalizacji konsumenta nie będzie (na ogół) rozwiązaniem wewnętrznym i jako takie należy sprawdzić poziom użyteczności w przypadkach granicznych (wydaj cały budżet na dobro x, wydaj cały budżet na dobro y), aby zobaczyć, które jest rozwiązaniem. Szczególnym przypadkiem jest sytuacja, gdy (stała) MRS jest równa stosunkowi ceny (na przykład oba towary mają tę samą cenę i te same współczynniki w funkcji użyteczności). W takim przypadku dowolna kombinacja tych dwóch towarów jest rozwiązaniem problemu konsumenta.

Reakcja na zmiany cen

Dla danego poziomu realnego bogactwa tylko ceny względne mają znaczenie dla konsumentów, a nie ceny bezwzględne. Gdyby konsumenci reagowali na zmiany cen nominalnych i nominalnego bogactwa, nawet jeśli względne ceny i realne bogactwo pozostały niezmienione, byłby to efekt zwany iluzją pieniądza . Matematyczne warunki pierwszego rzędu dla maksimum problemu konsumenckiego gwarantują, że popyt na każde dobro jest jednorodny stopnia zero łącznie w cenach nominalnych i nominalnym bogactwie, więc nie ma iluzji pieniężnej.

Kiedy zmieniają się ceny towarów, optymalna konsumpcja tych dóbr będzie zależała od efektu substytucyjnego i dochodowego. Efekt substytucji mówi , że jeśli popyt na oba dobra jest jednorodny, gdy cena jednego dobra spada (przy zachowaniu ceny drugiego dobra na stałym poziomie), konsument będzie konsumował więcej tego dobra, a mniej drugiego, ponieważ staje się ono relatywnie tańsze. To samo dotyczy wzrostu ceny jednego dobra, konsumenci będą kupować mniej tego dobra, a więcej drugiego.

Efekt dochodowy występuje wtedy, gdy zmiana cen towarów powoduje zmianę dochodu. Jeśli cena jednego dobra rośnie, wówczas dochód maleje (konsumpcja tego samego pakietu jest bardziej kosztowna niż wcześniej), to samo dzieje się, gdy cena dobra spada, dochód wzrasta (tańsze konsumpcja tego samego pakietu, dzięki czemu mogą konsumować więcej pożądanej kombinacji dóbr).

Reakcja na zmiany dochodów

Rysunek 5: To pokazuje, jak zmienia się optymalny pakiet konsumenta, gdy jego dochód wzrasta.

Jeśli dochód konsumenta wzrośnie, jego linia budżetowa zostanie przesunięta na zewnątrz i będzie miał teraz większy dochód do wydania na dobro x, dobro y lub oba, w zależności od preferencji dotyczących każdego dobra. gdyby oba dobra x i y były dobrami normalnymi , to konsumpcja obu dóbr wzrosłaby, a pakiet optymalny przesunąłby się z A do C (patrz rysunek 5). Gdyby x lub y były dobrami niższego rzędu , popyt na nie zmniejszałby się wraz ze wzrostem dochodu (optymalna paczka znajdowałaby się w punkcie B lub C).

Ograniczona racjonalność

po więcej informacji patrz: Ograniczona racjonalność

W praktyce konsument nie zawsze może wybrać optymalny pakiet. Na przykład może wymagać zbyt wiele przemyśleń lub zbyt wiele czasu. Ograniczona racjonalność jest teorią wyjaśniającą to zachowanie. Przykładami alternatyw dla maksymalizacji użyteczności ze względu na ograniczoną racjonalność są; spełnianie , eliminacja przez aspekty i mentalna heurystyka księgowa.

Heurystyka satysfakcji polega na tym, że konsument określa poziom aspiracji i szuka, aż znajdzie opcję, która to spełnia, uzna tę opcję za wystarczająco dobrą i przestanie szukać.
Eliminacja według aspektów polega na określeniu poziomu dla każdego aspektu pożądanego produktu i wyeliminowaniu wszystkich innych opcji, które nie spełniają tego wymogu, np. ceny poniżej 100 USD, koloru itp., aż pozostanie tylko jeden produkt, który jest uważany za produkt konsument wybierze.
Mentalna heurystyka rachunkowości : w tej strategii widać, że ludzie często przypisują subiektywne wartości swoim pieniądzom w zależności od preferencji dotyczących różnych rzeczy. Osoba opracuje mentalne konta dla różnych wydatków, przydzieli na nie swój budżet, a następnie spróbuje zmaksymalizować użyteczność na każdym koncie.

Pojęcia pokrewne

Związek między funkcją użyteczności a popytem Marshalla w problemie maksymalizacji użyteczności odzwierciedla związek między funkcją wydatków a popytem Hicksa w problemie minimalizacji wydatków . W minimalizacji wydatków podawany jest poziom użyteczności, podobnie jak ceny towarów, rolą konsumenta jest znalezienie minimalnego poziomu wydatków niezbędnych do osiągnięcia tego poziomu użyteczności.

Reguła utylitarnego wyboru społecznego to zasada, która mówi, że społeczeństwo powinno wybrać alternatywę, która maksymalizuje sumę użyteczności . Podczas gdy maksymalizacja użyteczności jest dokonywana przez jednostki, maksymalizacja sumy użyteczności jest wykonywana przez społeczeństwo.

Zobacz też

^ Levin, Jonothan (2004). Teoria konsumenta . Uniwersytet Stanford. s. 4–6.
^ Salcedo, Bruno (2017). Reprezentacje użytkowe . Uniwersytet Cornella. s. 18–19.
^ ^a ^b Zarząd, Simon (2009). Problem maksymalizacji użyteczności . Wydział Ekonomii, UCLA. s. 10–17.
^ Wybór, preferencje i użyteczność . prasa uniwersytetu Princeton. ndp 14.
^ ^a ^b Maksymalizacja użyteczności i popyt . Biblioteka Uniwersytetu Minnesoty. 2011. s. rozdział 7.2.
^ Uniwersytet Ryżowy (nd). „Jak zmiany dochodów i cen wpływają na wybory konsumpcyjne” . Książki prasowe . Źródło 22 kwietnia 2021 r . {{ cite web }} : CS1 maint: stan adresu URL ( link )
^ Wheeler, Grzegorz (2018). ograniczona racjonalność . Stanford Encyklopedia filozofii.
^ „Model eliminacji według aspektów” . Uniwersytet Monasha . 2018 . Źródło 20 kwietnia 2021 r . {{ cite web }} : CS1 maint: stan adresu URL ( link )
^ „Dlaczego mniej myślimy o niektórych zakupach niż o innych?” . Laboratorium decyzyjne . 2021 . Źródło 20 kwietnia 2021 r . {{ cite web }} : CS1 maint: stan adresu URL ( link )

Linki zewnętrzne

[1] Levin, Jonothan (2004). Teoria konsumenta . Uniwersytet Stanford. s. 4–6.

[2] Salcedo, Bruno (2017). Reprezentacje użytkowe . Uniwersytet Cornella. s. 18–19.

[:0-3] Zarząd, Simon (2009). Problem maksymalizacji użyteczności . Wydział Ekonomii, UCLA. s. 10–17.

[4] Wybór, preferencje i użyteczność . prasa uniwersytetu Princeton. ndp 14.

[:1-5] Maksymalizacja użyteczności i popyt . Biblioteka Uniwersytetu Minnesoty. 2011. s. rozdział 7.2.

[6] Uniwersytet Ryżowy (nd). „Jak zmiany dochodów i cen wpływają na wybory konsumpcyjne” . Książki prasowe . Źródło 22 kwietnia 2021 r . {{ cite web }} : CS1 maint: stan adresu URL ( link )

[7] Wheeler, Grzegorz (2018). ograniczona racjonalność . Stanford Encyklopedia filozofii.

[8] „Model eliminacji według aspektów” . Uniwersytet Monasha . 2018 . Źródło 20 kwietnia 2021 r . {{ cite web }} : CS1 maint: stan adresu URL ( link )

[9] „Dlaczego mniej myślimy o niektórych zakupach niż o innych?” . Laboratorium decyzyjne . 2021 . Źródło 20 kwietnia 2021 r . {{ cite web }} : CS1 maint: stan adresu URL ( link )