Szybki odwrotny pierwiastek kwadratowy

Obliczenia oświetlenia i odbicia, podobnie jak w grze wideo OpenArena , wykorzystują szybki kod odwrotnego pierwiastka kwadratowego do obliczenia kątów padania i odbicia.

Szybki odwrotny pierwiastek kwadratowy $,$ czasami określany jako Fast InvSqrt () lub przez stałą szesnastkową 0x5F3759DF , to algorytm, który szacuje odwrotność lub odwrotność multiplikatywna) pierwiastka kwadratowego z 32-bitowej liczby zmiennoprzecinkowej w formacie zmiennoprzecinkowym IEEE 754 x $\ displaystyle x}$ . Ta operacja jest używana w cyfrowym przetwarzaniu sygnału w celu normalizacji wektora, na przykład skalowania go do długości 1. Na przykład programy grafiki komputerowej używają odwrotnych pierwiastków kwadratowych do obliczania kątów padania i odbicia dla oświetlenia i cieniowania . Wyprzedzony przez podobne algorytmy gier wideo, ten jest najbardziej znany z implementacji w 1999 roku w Quake III Arena , strzelance z perspektywy pierwszej osoby, mocno opartej na grafice 3D . Algorytm zaczął pojawiać się na forach publicznych dopiero w latach 2002-2003. Obliczanie pierwiastków kwadratowych zwykle zależy od wielu operacji dzielenia, które w przypadku liczb zmiennoprzecinkowych są kosztowne obliczeniowo . Szybki odwrotny kwadrat generuje dobre przybliżenie z tylko jednym krokiem podziału.

Algorytm akceptuje 32-bitową liczbę zmiennoprzecinkową jako dane wejściowe i przechowuje połowę wartości do późniejszego wykorzystania. Następnie, traktując bity reprezentujące liczbę zmiennoprzecinkową jako 32-bitową liczbę całkowitą, logiczne przesunięcie o jeden bit w prawo i wynik odejmuje od liczby 0x 5F3759DF (w zapisie dziesiętnym: 1 597 463 007), która jest liczbą zmiennoprzecinkową reprezentacja przybliżenia $2 ^ {127}}}}$ { Powoduje to pierwsze przybliżenie odwrotności pierwiastka kwadratowego danych wejściowych. Traktując bity ponownie jako liczbę zmiennoprzecinkową, wykonuje jedną iterację metody Newtona , uzyskując dokładniejsze przybliżenie.

Algorytm był często błędnie przypisywany Johnowi Carmackowi , ale w rzeczywistości kod jest oparty na niepublikowanym artykule Williama Kahana i KC Ng, opublikowanym w maju 1986 roku. Ardent Computing pod koniec lat 80.

Wraz z późniejszymi ulepszeniami sprzętu, zwłaszcza instrukcją x86 SSE rsqrtss , ta metoda nie ma ogólnego zastosowania w komputerach ogólnego przeznaczenia, chociaż pozostaje interesującym przykładem zarówno historycznie, jak i dla bardziej ograniczonych maszyn, takich jak tanie systemy wbudowane. Jednak coraz więcej producentów systemów wbudowanych włącza trygonometryczne i inne akceleratory matematyczne, takie jak CORDIC , unikając potrzeby stosowania takich algorytmów.

Motywacja

Normalne powierzchni są szeroko stosowane w obliczeniach oświetlenia i cieniowania, co wymaga obliczenia norm dla wektorów. Tutaj pokazano pole wektorów normalnych do powierzchni.

Dwuwymiarowy przykład użycia normalnego

znalezienia

kąta odbicia od kąta padania; w tym przypadku na świetle odbijającym się od zakrzywionego lustra. Szybki odwrotny pierwiastek kwadratowy służy do uogólnienia tego obliczenia na przestrzeń trójwymiarową.

Odwrotny pierwiastek kwadratowy liczby zmiennoprzecinkowej jest używany do obliczania znormalizowanego wektora . Programy mogą wykorzystywać znormalizowane wektory do określania kątów padania i odbicia . Programy graficzne 3D muszą wykonywać miliony tych obliczeń co sekundę, aby symulować oświetlenie. Kiedy kod został opracowany na początku lat 90., większość mocy przetwarzania zmiennoprzecinkowego nie nadążała za szybkością przetwarzania liczb całkowitych. Było to kłopotliwe dla programów graficznych 3D przed pojawieniem się specjalistycznego sprzętu do obsługi transformacji i oświetlenia .

Długość wektora określa się obliczając jego normę euklidesową : pierwiastek kwadratowy z sumy kwadratów składowych wektora . Gdy każdy składnik wektora zostanie podzielony przez tę długość, nowy wektor będzie wektorem jednostkowym skierowanym w tym samym kierunku. W programie graficznym 3D wszystkie wektory są w przestrzeni trójwymiarowej $(v_ {1} ,v_{2},v_{3})}$ więc byłby to wektor $Displaystyle$ .

{\ Displaystyle \| {\ pogrubiony symbol {v}} \ | = {\ sqrt {v_ {1} ^ {2} + v_ {2} ^ {2 }+v_{3}^{2}}}}

jest normą euklidesową wektora.

{\ Displaystyle {\ boldsymbol {\ kapelusz {v}}} = {\ Frac {\ boldsymbol {v}} {\ lewo \ | {\ boldsymbol {v}} \ prawo \ |}} }

$+$ znormalizowanym (jednostkowym) wektorem, używającym ${ 1}^{2}+v_{2}^{2}+v_{3}^{2}}$ v .

{\ Displaystyle {\ pogrubiony symbol {\ kapelusz {v}}} = {\ Frac {\ pogrubiony symbol {v}} {\ sqrt {\ lewo \ | {\ pogrubiony symbol {v}} \ prawo \|^{2}}}}}

który wiąże wektor jednostkowy z odwrotnością pierwiastka kwadratowego składowych odległości. Odwrotny pierwiastek kwadratowy można wykorzystać do obliczenia, ponieważ to równanie jest równoważne z ${\ Displaystyle {\ boldsymbol {\ hat {v}}}}$

{\ Displaystyle {\ pogrubiony symbol {\ kapelusz {v}}} = {\ pogrubiony symbol {v}} \ {\ Frac {1} {\ sqrt {\ lewo \ | {\ pogrubiony symbol {v}}\prawo\|^{2}}}}}

gdzie wyraz ułamkowy jest odwrotnością pierwiastka kwadratowego z ${\ Displaystyle \| {\ boldsymbol {v}} \|^ {2}}$ .

W tamtym czasie dzielenie zmiennoprzecinkowe było generalnie drogie w porównaniu z mnożeniem; szybki algorytm odwrotnego pierwiastka kwadratowego omijał krok dzielenia, dając mu przewagę wydajności.

Przegląd kodu

Poniższy kod to szybka implementacja odwrotnego pierwiastka kwadratowego z Quake III Arena , pozbawiona dyrektyw preprocesora C , ale zawierająca dokładny oryginalny tekst komentarza:

    

	 
	  
	    

	    
	   
	                               
	                        
	        
	                  


	 
 float  Q_rsqrt  (  liczba  zmiennoprzecinkowa  )  {  długi  i  ;  liczba zmiennoprzecinkowa  x2  ,  y  ;  const  float  trzy połówki  =  1,5F  ;  x2  =  liczba  *  0,5F  ;  y  =  liczba  ;  ja  =  *  (  długi  *  )  &  y  ;  // złe hakowanie na poziomie bitów zmiennoprzecinkowych  i  =  0x5f3759df  -  (  i  >>  1  );  //co kurwa?  y  =  *  (  liczba zmiennoprzecinkowa  *  )  &  ja  ;  y  =  y  *  (  trzy połówki  -  (  x2  *  y  *  y  )  );  // 1. iteracja  // y = y * ( trzy połówki - ( x2 * y * y ) ); // Druga iteracja, można to usunąć   return  y  ;  }

W tamtym czasie ogólną metodą obliczania odwrotnego pierwiastka kwadratowego było obliczenie przybliżenia dla , a następnie skorygowanie tego przybliżenia inną metodą $,$ uzyskania w dopuszczalnym zakresie błędu rzeczywistego wyniku. Powszechne metody oprogramowania stosowane na początku lat 90. polegały na rysowaniu przybliżeń na podstawie tabeli przeglądowej . Kluczem szybkiego odwrotnego pierwiastka kwadratowego było bezpośrednie obliczenie przybliżenia przy użyciu struktury liczb zmiennoprzecinkowych, co okazało się szybsze niż przeszukiwanie tabeli. Algorytm był około cztery razy szybszy niż obliczanie pierwiastka kwadratowego inną metodą i obliczanie odwrotności za pomocą dzielenia zmiennoprzecinkowego. Algorytm został zaprojektowany z IEEE 754-1985 , ale badanie przeprowadzone przez Chrisa Lomonta wykazało, że można go zaimplementować w innych specyfikacjach zmiennoprzecinkowych.

Korzyści w zakresie szybkości oferowane przez sztuczkę z szybkim odwrotnym pierwiastkiem kwadratowym wynikały z traktowania 32-bitowego słowa zmiennoprzecinkowego jako liczby całkowitej , a następnie odejmowania go od „ magicznej ” stałej, 0x 5F3759DF . To odejmowanie liczb całkowitych i przesunięcie bitów skutkuje wzorem bitowym, który po ponownym zdefiniowaniu jako liczba zmiennoprzecinkowa jest przybliżonym przybliżeniem odwrotności pierwiastka kwadratowego z liczby. Wykonywana jest jedna iteracja metody Newtona w celu uzyskania pewnej dokładności i kod jest gotowy. Algorytm generuje dość dokładne wyniki przy użyciu unikalnego pierwszego przybliżenia dla metody Newtona ; jest jednak znacznie wolniejszy i mniej dokładny niż użycie instrukcji SSE rsqrtss na procesorach x86, również wydanych w 1999 roku.

Działający przykład

Na przykład liczba może być użyta do obliczenia $Displaystyle {\ Frac {1} {\ sqrt {x}}} \$ $\$ } Poniżej zilustrowano pierwsze kroki algorytmu:

0011_1110_0010_0000_0000_0000_0000_0000 Wzór bitowy zarówno x, jak i i 0001_1111_0001_0000_0000_0000_0000_0000 Przesunięcie w prawo o jedną pozycję: (i >> 1) 0101_1111_0011_0111_010 1_1001_1101_1111 Magiczna liczba 0x5F3759DF 0100_0000_0010_0111_0101_1001_1101_1111 Wynik 0x5F3759DF - (i >> 1)

Interpretacja jako 32-bitowa reprezentacja IEEE:

 0_01111100_010000000000000000000000 1,25 × 2 ⁻³ 0_00111110_001000000000000000000000 1,125 × 2 ⁻⁶⁵ 0_10111110_011011101011001110 11111 1.432430... × 2 ⁶³ 0_10000000_01001110101100111011111 1.307430... × 2 ¹

$błąd$ daje przybliżenie, które około 3,4%. Po jednej iteracji metody Newtona końcowy wynik to $0,17$ wynoszący zaledwie

Unikanie nieokreślonego zachowania

Zgodnie ze standardem C reinterpretacja wartości zmiennoprzecinkowej jako liczby całkowitej przez rzutowanie, a następnie dereferencja wskaźnika do niej, jest nieprawidłowa ( niezdefiniowane zachowanie ). Innym sposobem byłoby umieszczenie wartości zmiennoprzecinkowej w anonimowej unii zawierającej dodatkowy 32-bitowy element całkowity bez znaku, a dostęp do tej liczby całkowitej zapewnia widok zawartości wartości zmiennoprzecinkowej na poziomie bitów. Jednak przebijanie typów przez unię jest również niezdefiniowanym zachowaniem w C++.

 
	
  

	 
		    
		 
	       
	       
	          
	 
 #include  <stdint.h>  // uint32_t  float  Q_rsqrt  (  liczba  zmiennoprzecinkowa  )  {  union  {  float  f  ;  uint32_t  i  ;  }  konw.  =  {  .  f  =  liczba  };  konw  .  i  =  0x5f3759df  -  (  konw  .  ja  >>  1  );  konw  .  fa  *=  1,5F  -  (  liczba  *  0,5F  *  konw  .  fa  *  konw  .  f  );  konw  .  zwrotna  f  ;  }

W C++ zwykłą metodą implementacji rzutowania tej funkcji jest std::bit_cast C++20 . Pozwala to również funkcji działać w constexpr :

 
 
 

    

	 

	    
		    
	           
 #include  <bit>  #include  <limity>  #include  <cstdint>  constexpr  float  Q_rsqrt  (  liczba  zmiennoprzecinkowa  )  noexcept  {  static_assert  (  std  ::  numeric_limits  <  float  >::  is_iec559  );  // (włączone tylko na IEEE 754)  float  const  y  =  std  ::  bit_cast  <  float  >  (  0x5f3759df  -  (  std  ::  bit_cast  <  std  ::  uint32_t  >  (  number  )  >>  1  ));  zwróć  y  *  (  1,5 f  -  (  liczba  *  0,5 f  *  y  *  y  ));  }

Algorytm

Algorytm oblicza wykonując następujące kroki: ${\ displaystyle {\ frac {1} {\ sqrt {x}}}}$

Przypisz argumentowi $całkowitą$ jako sposób obliczenia przybliżenia logarytmu binarnego ${\ Displaystyle \ log _ {2} (x)}$
Użyj tego przybliżenia, aby obliczyć przybliżenie ${\ Displaystyle \ log _ {2} \ lewo ({\ Frac {1} {\ sqrt {x}} }\right)=-{\frac {1}{2}}\log _{2}(x)}$
Alias z powrotem do liczby zmiennoprzecinkowej, jako sposób obliczenia przybliżenia wykładniczego podstawy 2
Doprecyzuj przybliżenie za pomocą pojedynczej iteracji metody Newtona.

Reprezentacja zmiennoprzecinkowa

Ponieważ ten algorytm w dużej mierze opiera się na reprezentacji bitowej liczb zmiennoprzecinkowych o pojedynczej precyzji, poniżej przedstawiono krótki przegląd tej reprezentacji. Aby zakodować niezerową liczbę rzeczywistą $zmiennoprzecinkową o pojedynczej precyzji, pierwszym$ jest zapisanie jako znormalizowanej liczby binarnej: ${\ displaystyle x}$

{\ Displaystyle {\ rozpocząć {wyrównane} x & = \ pm 1.b_ {1} b_ {2} b_{3}\ldots \times 2^{e_{x}}\\&=\pm 2^{e_{x}}(1+m_{x})\end{wyrównane}}}

gdzie wykładnik jest liczbą całkowitą, $)$ $\ Displaystyle m_ {x} \ in [0,1$ i ${\ Displaystyle 1.b_ {1} b_ {2} b_ {3} \ ldots}$ jest binarną reprezentacją „znaczenia” ${\ Displaystyle (1 + m_ {x})}$ . Ponieważ pojedynczy bit przed punktem w mantysach jest zawsze 1, nie musi być przechowywany. Z tej postaci obliczane są trzy liczby całkowite bez znaku:

${\ Displaystyle S_ {x}}$ , „bit znaku”, wynosi ${\ Displaystyle 0}$ $,$ jeśli jest dodatni, a $\ Displaystyle 1}$ ujemny lub zerowy (1 bit)
${\ Displaystyle E_ {x} = e_ {x} + B}$ to „obciążony wykładnik”, gdzie ${\ Displaystyle B = 127}$ to „ odchylenie wykładnika ” (8 bitów)
${\ Displaystyle M_ {x} = m_ {x} \ razy L}$ gdzie ${\ Displaystyle L = 2 ^ {23}}$ (23 bity)

Pola te są następnie pakowane, od lewej do prawej, do kontenera 32-bitowego.

$_$ przykład _ Normalizacja daje: ${\ displaystyle x}$

{\ Displaystyle x = + 2 ^ {- 3} (1 + 0,25)}

a zatem trzy pola liczb całkowitych bez znaku to:

${\ displaystyle S = 0}$
${\ Displaystyle E = -3 + 127 = 124 = 0111 \ 1100_ {2}}$
${\ Displaystyle M = 0,25 \ razy 2 ^ {23} = 2 \ 097 \ 152 = 0010 \ 0000 \ 0000 \ 0000 \ 0000 \ 0 000_{ 2}}$

te pola są spakowane, jak pokazano na poniższym rysunku:

Aliasing do liczby całkowitej jako przybliżony logarytm

Gdyby $obliczyć$ bez komputera lub kalkulatora, ${\ Displaystyle \ log _ {b} \ lewo ({\ Frac {1} {\ sqrt {x}}} \ prawej) =\log _{b}\left(x^{-{\frac {1}{2}}}\right)=-{\frac {1}{2}}\log _{b}(x)}$ byłaby tabela logarytmów wraz z , co jest ważne dla każdej podstawy ${\ displaystyle b}$ . Szybki odwrotny pierwiastek kwadratowy opiera się na tej tożsamości oraz na fakcie, że aliasowanie liczby zmiennoprzecinkowej32 do liczby całkowitej daje przybliżone przybliżenie jej logarytmu. Oto jak:

Jeśli jest dodatnią liczbą normalną : ${\ displaystyle x}$

{\ Displaystyle x = 2 ^ {e_ {x}} (1 + m_ {x})}

Następnie

{\ Displaystyle \ log _ {2} (x) = e_ {x} + \ log _ {2} (1 + m_ {x} )}

a ponieważ logarytm po prawej stronie można przybliżyć ${\ Displaystyle m_ {x} \ in [0,1)}$

{\ Displaystyle \ log _ {2} (1 + m_ {x}) \ około m_ {x} + \ sigma}

gdzie jest wolnym parametrem używanym do dostrojenia $.$ Na przykład ${\ Displaystyle \ sigma = 0}$ daje dokładne wyniki na obu końcach przedziału, podczas gdy ${\ displaystyle \sigma ={\frac {1}{2}}-{\frac {1+\ln(\ln(2))}{2\ln(2)}}\około 0,0430357} daje optymalne przybliżenie$ ( tzw . najlepiej w sensie jednolitej normy błędu). Jednak ta wartość nie jest wykorzystywana przez algorytm, ponieważ nie uwzględnia kolejnych kroków.

Liczba całkowita aliasowana do liczby zmiennoprzecinkowej (na niebiesko), w porównaniu do przeskalowanego i przesuniętego logarytmu (na szaro).

Mamy więc do czynienia z przybliżeniem

{\ Displaystyle \ log _ {2} (x) \ około e_ {x} + m_ {x} + \ sigma.}

${\ displaystyle I_ {x}$ zmiennoprzecinkowego wzorca bitowego jako liczby całkowitej daje $}$

{\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} & = E_ {x} L + M_ {x} \\ & = L (e_ {x} + B + m_ {x}) \\& = L (e_ {x}+m_{x}+\sigma +B-\sigma )\\&\około L\log _{2}(x)+L(B-\sigma ).\end{wyrównane}}}

Następnie okazuje się, że $_$ $(x)}$ { , jak pokazano na rysunku prawo. Innymi słowy, ${\ Displaystyle \ log _ {2} (x)}$ jest przybliżony przez

{\ Displaystyle \ log _ {2} (x) \ około {\ Frac {I_ {x}} {L}} - (B- \ sigma).}

Pierwsze przybliżenie wyniku

Obliczenie jest oparte na tożsamości ${\ Displaystyle y = {\ Frac {1} {\ sqrt {x}}}}$

{\ Displaystyle \ log _ {2} (y) = - {\ tfrac {1} {2}} \ log _ {2} (x)}

Korzystając z przybliżenia powyższego logarytmu, zastosowanego zarówno do $,$ jak i ${\ displaystyle x}$ , powyższe równanie daje:

{\ Displaystyle {\ Frac {I_ {y}} {L}} - (B- \ sigma) \ ok - {\frac {1}{2}}\left({\frac {I_{x}}{L}}-(B-\sigma)\right)}

Zatem przybliżenie to : ${\ displaystyle I_ {y}}$

{\ Displaystyle I_ {y} \ około {\ tfrac {3} {2}} L (B- \ sigma) - {\ tfrac {1} 2}}Ja_{x}}

co jest zapisane w kodzie jako

          ja  =  0x5f3759df  -  (  ja  >>  1  );

Pierwszy termin powyżej to liczba magiczna

{\ Displaystyle {\ tfrac {3} {2}} L (B- \ sigma) = {\ mathtt {0x5F3759DF}}}

z którego można wywnioskować, że ${\ Displaystyle \ sigma \ około 0,0450466}$ . Drugi wyraz, $przesunięcie$ $jedną$ o w prawo

Metoda Newtona

Względny błąd między obliczeniami bezpośrednimi a szybkim odwrotnym pierwiastkiem kwadratowym przeprowadzającym 0, 1, 2, 3 i 4 iteracje metody znajdowania pierwiastków Newtona. Należy zauważyć, że przyjmuje się podwójną precyzję, a najmniejszą możliwą do przedstawienia różnicę między dwiema liczbami podwójnej precyzji uzyskuje się po przeprowadzeniu 4 iteracji.

Z ${\ Displaystyle y}$ jako odwrotnym pierwiastkiem kwadratowym, ${\ Displaystyle f (y) = {\ Frac {1} {y ^ {2}}} -x = 0 }$ . Przybliżenie otrzymane we wcześniejszych krokach można udoskonalić za pomocą metody znajdowania pierwiastków , metody, która znajduje zero funkcji . Algorytm wykorzystuje $}}$ Newtona : jeśli istnieje przybliżenie dla , $1$ może { displaystyle $+$ ${\ Displaystyle y_ {n} - {\ Frac {f (y_ {n})} {f' (y_ {n})}$ fa } gdzie jest pochodną ${$ ${\ Displaystyle f (y)$ \ $}$ } . Dla powyższego ${\ Displaystyle f (y)}$ ,

{\ Displaystyle y_ {n + 1} = {\ Frac {y_ {n} \ lewo (3-xy_ {n} ^ {2} \ prawej) {2}}}

gdzie ${\ Displaystyle f (y) = {\ Frac {1} {y ^ {2}}} -x}$ i ${\ Displaystyle f'(y)=-{\frac {2}{y^{3}}}}$ .

Traktując jako liczbę $zmiennoprzecinkową$ , = y * (trzy połówki - x/2 * y * y); jest równa

{\ Displaystyle y_ {n + 1} = y_ {n} \ lewo ({\ Frac {3} {2}} - {\ Frac {x} {2}} y_ {n} ^ {2} \ prawej) = {\frac {y_{n}\left(3-xy_{n}^{2}\right)}{2}}.}

Powtarzając ten krok, używając danych wyjściowych funkcji ( ) jako danych wejściowych następnej iteracji, algorytm powoduje zbieżność do odwrotnego kwadratu ${\ displaystyle y_$ $n + 1}}$ źródło. Na potrzeby silnika Quake III wykorzystano tylko jedną iterację. Druga iteracja pozostała w kodzie, ale została wykomentowana .

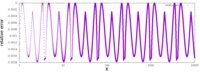
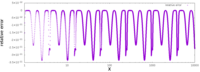
Dokładność

Jak wspomniano powyżej, przybliżenie jest bardzo dokładne. Pojedynczy wykres po prawej stronie przedstawia błąd funkcji (czyli błąd aproksymacji po jej poprawieniu przez wykonanie jednej iteracji metody Newtona) dla danych wejściowych zaczynających się od 0,01, gdzie biblioteka standardowa daje wynik 10,0 , a InvSqrt() daje 9,982522, co daje względną różnicę 0,0017478, czyli 0,175% wartości prawdziwej, 10. Od tego momentu błąd bezwzględny spada tylko, a błąd względny pozostaje w tych samych granicach we wszystkich rzędach wielkości.

Historia

William Kahan i KC Ng z Berkeley napisali nieopublikowany artykuł w maju 1986 roku, w którym opisali, jak obliczyć pierwiastek kwadratowy za pomocą technik manipulacji bitami, po których nastąpiły iteracje Newtona. Pod koniec lat 80. Cleve Moler z Ardent Computer dowiedział się o tej technice i przekazał ją swojemu współpracownikowi Gregowi Walshowi. Greg Walsh opracował słynny stały i szybki algorytm odwrotnego pierwiastka kwadratowego. Gary Tarolli był konsultantem dla Kubota, firmy finansującej wówczas Ardent, i prawdopodobnie wprowadził algorytm do 3dfx Interactive około 1994 roku.

Jim Blinn zademonstrował proste przybliżenie odwrotności pierwiastka kwadratowego w kolumnie z 1997 roku dla IEEE Computer Graphics and Applications . Inżynieria wsteczna innych współczesnych gier wideo 3D odkryła odmianę algorytmu w grze Activision Interstate '76 z 1997 roku .

Quake III Arena , strzelanka z perspektywy pierwszej osoby , została wydana w 1999 roku przez id Software i wykorzystywała algorytm. Brian Hook mógł przenieść algorytm z 3dfx do id Software. Kopie szybkiego odwrotnego kodu pierwiastka kwadratowego pojawiły się w Usenecie i innych forach już w 2002 lub 2003 roku. Pojawiły się spekulacje, kto napisał algorytm i jak wyprowadzono stałą; niektórzy domyślili się, że John Carmack . Pełny kod źródłowy Quake III został udostępniony na QuakeCon 2005 , ale nie dostarczył żadnych odpowiedzi. Na pytanie o autorstwo udzielono odpowiedzi w 2006 roku.

W 2007 roku algorytm został zaimplementowany w niektórych dedykowanych sprzętowych modułach cieniujących wierzchołki przy użyciu programowalnych przez użytkownika macierzy bramek (FPGA).

Kolejne ulepszenia

magiczny numer

Nie wiadomo dokładnie, w jaki sposób ustalono dokładną wartość magicznej liczby. Chris $Lomont$ opracował funkcję minimalizującą błąd aproksymacji , wybierając magiczną liczbę zakresu. Najpierw obliczył optymalną stałą dla kroku aproksymacji liniowej jako 0x5F37642F , blisko 0x5F3759DF , ale ta nowa stała dała nieco mniejszą dokładność po jednej iteracji metody Newtona. Następnie Lomont szukał stałego optymalnego nawet po jednej i dwóch iteracjach Newtona i znalazł 0x5F375A86 , który jest dokładniejszy niż oryginał na każdym etapie iteracji. Zakończył pytaniem, czy dokładna wartość pierwotnej stałej została wybrana metodą wyprowadzenia, czy metodą prób i błędów . Lomont powiedział, że magiczna liczba dla podwójnego rozmiaru 64-bitowego IEEE754 to 0x5FE6EC85E7DE30DA , ale później Matthew Robertson wykazał, że jest to dokładnie 0x5FE6EB50C7B537A9 .

Jan Kadlec zredukował błąd względny o kolejny współczynnik 2,7, dostosowując również stałe w pojedynczej iteracji metody Newtona, docierając po wyczerpujących poszukiwaniach do

	        
	            
	  konw  .  i  =  0x5F1FFFF9  -  (  konw  .  ja  >>  1  );  konw  .  f  *=  0,703952253f  *  (  2,38924456f  -  x  *  zw  .  fa  *  zw  .  f  );  konw  .  zwrotna  f  ;

Dla liczb zmiennoprzecinkowych pojedynczej precyzji dostępna jest teraz kompletna analiza matematyczna służąca do określania liczby magicznej.

Brak znalezienia

Pośrednim zastosowaniem jednej lub dwóch iteracji metody Newtona pod względem szybkości i dokładności jest pojedyncza iteracja metody Halleya . W tym przypadku metoda Halleya jest równoważna zastosowaniu metody Newtona ze wzorem wyjściowym ${\ Displaystyle f (y) = {\ Frac {1} {y ^ {1/2}}}-xy^{3/2}=0}$ . Krok aktualizacji jest wtedy

{\ Displaystyle y_ {n + 1} = y_ { n}-{\frac {f(y_{n})}{f'(y_{n})}}=y_{n}\left({\frac {3+xy_{n}^{2}}{ 1+3xy_{n}^{2}}}\prawo),}

gdzie implementacja powinna obliczyć $raz$ , za pomocą

Zobacz też

Notatki

Bibliografia

Blinn, Jim (lipiec 1997). „Sztuczki zmiennoprzecinkowe”. IEEE Grafika komputerowa i aplikacje . 17 (4): 80. doi : 10.1109/38.595279 .
Blinn, Jim (2003). Jim Blinn's Corner: Notacja, notacja notacji . Morgana Kaufmanna. ISBN 1-55860-860-5 .
Eberly, David (2001). Projekt silnika gry 3D . Morgana Kaufmanna. ISBN 978-1-55860-593-0 .
Goldberg, David (1991). „Co każdy informatyk powinien wiedzieć o arytmetyce zmiennoprzecinkowej”. Ankiety komputerowe ACM . 23 (1): 5–48. doi : 10.1145/103162.103163 . S2CID 222008826 .
Hardy, Godfrey (1908). Kurs czystej matematyki . Cambridge, Wielka Brytania : Cambridge University Press . ISBN 0-521-72055-9 .
Hennessey, John; Patterson, David A. (1998). Organizacja i projektowanie komputerów (wyd. 2). San Francisco, Kalifornia: Wydawcy Morgan Kaufmann. ISBN 978-1-55860-491-9 .
Lomont, Chris (luty 2003). „Szybki odwrotny pierwiastek kwadratowy” (PDF) . Źródło 2009-02-13 .
McEniry, Charles (sierpień 2007). „Matematyka stojąca za kodem funkcji szybkiego odwrotnego pierwiastka kwadratowego” (PDF) . Zarchiwizowane od oryginału (PDF) w dniu 11.05.2015 r.
Middendorf, Lars; Mühlbauer, Feliks; Umlauf, George; Bodba, Christophe (1 czerwca 2007). „Wbudowany moduł cieniujący wierzchołki w FPGA” (PDF) . W Rettberg, Achin (red.). Projektowanie systemów wbudowanych: tematy, techniki i trendy . Konferencja robocza IFIP TC10: Międzynarodowe sympozjum systemów wbudowanych (IESS). i in. Irvine, Kalifornia : Springer. doi : 10.1007/978-0-387-72258-0_14 . ISBN 978-0-387-72257-3 . Zarchiwizowane (PDF) od oryginału w dniu 2019-05-01.
Striegel, Jason (2008-12-04). „Szybki odwrotny pierwiastek kwadratowy Quake'a” . Hackszine . O'Reilly Media . Zarchiwizowane od oryginału w dniu 15.02.2009 . Źródło 2013-01-07 .
IEEE Computer Society (1985), 754-1985 - Standard IEEE dla binarnej arytmetyki zmiennoprzecinkowej , Instytut Inżynierów Elektryków i Elektroników
Moroz, Leonid V.; Walczyk, Cezary J.; Hrynczyszyn, Andrij; Holimath, Vijay; Cieśliński, Jan L. (styczeń 2018). „Szybkie obliczanie odwrotności pierwiastka kwadratowego z wykorzystaniem podejścia analitycznego z magiczną stałą”. Matematyka stosowana i obliczenia . Elsevier Science Inc. 316 (C): 245–255. ar Xiv : 1603.04483 . doi : 10.1016/j.amc.2017.08.025 . S2CID 7494112 .

Dalsza lektura

Kushner, David (sierpień 2002). „Czarnoksiężnik Id”. widmo IEEE . 39 (8): 42–47. doi : 10.1109/MSPEC.2002.1021943 .

Linki zewnętrzne

0x5f3759df , dalsze badania dokładności i możliwości uogólnienia algorytmu przez Christiana Plesnera Hansena
Pochodzenie Fast InvSqrt() w Quake3
Kod źródłowy Quake III Arena ( zarchiwizowany w Software Heritage )
Implementacja InvSqrt w DESMOS
„Szybki odwrotny pierwiastek kwadratowy — algorytm Quake III” ( YouTube )