Metoda Heuna

W matematyce i informatyce metoda Heuna może odnosić się do ulepszonej lub zmodyfikowanej metody Eulera (to znaczy jawnej reguły trapezów ) lub podobnej dwustopniowej metody Runge-Kutty . Jej nazwa pochodzi od Karla Heuna i jest numeryczną procedurą rozwiązywania równań różniczkowych zwyczajnych (ODE) z zadaną wartością początkową . Oba warianty można postrzegać jako rozszerzenia metody Eulera na dwuetapowe metody Runge-Kutty drugiego rzędu.

Procedura obliczania numerycznego rozwiązania problemu z wartością początkową:

${\ Displaystyle y' (t) = f (t, y (t)), \ qquad \ qquad y (t_ { 0})=y_{0},}$

metodą Heuna jest najpierw obliczenie wartości pośredniej, $+1}}$$następnie$ ostatecznego przybliżenia ${\ Displaystyle {\ tylda {y}} _ {i +$ w następnym punkcie integracji.

${\ Displaystyle {\ tylda {y}} _ {i + 1} = y_ {i} + hf (t_ {i}, y_ {i })}$

${\ Displaystyle y_ {i + 1} = y_ {i} + {\ Frac {h} {2}} [f (t_ {i}, y_ {i}) + f (t_ {i + 1},{\tylda {y}}_{i+1})],}$

gdzie jest rozmiar kroku i $t$$\ Displaystyle t_ {i + 1} = t_ {i} + h$ .

Opis

Metoda Eulera jest używana jako podstawa metody Heuna. Metoda Eulera wykorzystuje linię styczną do funkcji na początku przedziału jako oszacowanie nachylenia funkcji w przedziale, zakładając, że jeśli rozmiar kroku jest mały, błąd będzie mały. Jednak nawet wtedy, gdy stosowane są bardzo małe rozmiary kroków, w przypadku dużej liczby kroków błąd zaczyna się kumulować, a oszacowanie odbiega od rzeczywistej wartości funkcjonalnej.

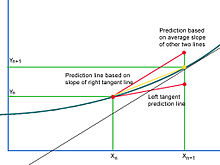
Tam, gdzie krzywa rozwiązania jest wklęsła w górę, jej linia styczna zaniży współrzędną pionową następnego punktu i odwrotnie w przypadku rozwiązania wklęsłego w dół. Idealna linia predykcji uderzyłaby w krzywą w następnym przewidywanym punkcie. W rzeczywistości nie ma sposobu, aby wiedzieć, czy rozwiązanie jest wklęsłe w górę, czy wklęsłe w dół, a zatem czy następny przewidywany punkt będzie przeszacowywał, czy niedoszacowywał swoją wartość pionową. Nie można również zagwarantować, że wklęsłość krzywej pozostanie spójna, a prognoza może przeszacowywać i niedoszacowywać w różnych punktach dziedziny rozwiązania. Metoda Heuna rozwiązuje ten problem, biorąc pod uwagę przedział obejmujący odcinek linii stycznej jako całość. Biorąc przykład wklęsły, lewa styczna linia przewidywania niedoszacowuje nachylenia krzywej dla całej szerokości przedziału od bieżącego punktu do następnego przewidywanego punktu. Jeśli weźmiemy pod uwagę linię styczną w prawym punkcie końcowym (co można oszacować za pomocą metody Eulera), ma to odwrotny problem. Punkty wzdłuż linii stycznej lewego punktu końcowego mają współrzędne pionowe, z których wszystkie zaniżają te, które leżą na krzywej rozwiązania, w tym prawy punkt końcowy rozważanego przedziału. Rozwiązaniem jest zwiększenie nachylenia o pewną wartość. Metoda Heuna uwzględnia linie styczne do krzywej rozwiązania w punkcie oba końce przedziału, jeden, który przeszacowuje , i drugi, który nie docenia idealnych współrzędnych pionowych. Linia prognozy musi być skonstruowana na podstawie samego nachylenia stycznej prawego punktu końcowego, aproksymowanej metodą Eulera. Jeśli to nachylenie przechodzi przez lewy punkt końcowy przedziału, wynik jest ewidentnie zbyt stromy, aby można go było użyć jako idealnej linii przewidywania, i przeszacowuje idealny punkt. Dlatego idealny punkt leży mniej więcej w połowie drogi między błędnym przeszacowaniem a niedoszacowaniem, czyli średnią z dwóch nachyleń.

Diagram przedstawiający użycie metody Heuna do znalezienia mniej błędnej prognozy w porównaniu z metodą Eulera niższego rzędu

Metoda Eulera służy do przybliżonego oszacowania współrzędnych następnego punktu w rozwiązaniu i dzięki tej wiedzy pierwotne oszacowanie jest ponownie przewidywane lub korygowane . Zakładając $\displaystyle \textstyle (x,y)}$ wielkość $po$ prawej stronie równania można traktować jako nachylenie szukanego $y$ , można to połączyć z oszacowaniem Eulera następnego punktu, aby uzyskać nachylenie linii stycznej w prawym punkcie końcowym. Następnie średnia z obu nachyleń jest używana do znalezienia poprawionych współrzędnych prawego końcowego przedziału.

Pochodzenie

${\ Displaystyle {\ tekst {nachylenie}} _ {\ tekst {lewo}} = f (x_ {i}, y_ {i})}$

${\ Displaystyle {\ tekst {nachylenie}} _ {\ tekst {po prawej}} = f (x_ {i} + h, y_ {i} + hf (x_{i},y_{i}))}$

${\ Displaystyle {\ tekst {Nachylenie}} _ {\ tekst {idealny}} = {\ Frac {1} {2}} ({\ tekst {Nachylenie}} _ {\ tekst {lewo }}+{\text{Nachylenie}}_{\text{prawo}})}$

Korzystając z zasady, że nachylenie linii jest równe wzrostowi/biegowi, współrzędne na końcu przedziału można znaleźć za pomocą następującego wzoru:

${\ Displaystyle {\ tekst {Nachylenie}} _ {\ tekst {ideał}} = {\ Frac {\ Delta y} {h}}} Δ$

$\ Displaystyle \ Delta y = h ({\ tekst {nachylenie}} _ {\ tekst {idealny}})}$

${\ Displaystyle x_ {i + 1} = x_ {i} + h$ } ${\ Displaystyle \ textstyle y_ {i + 1} = y_ {i} + \ Delta y} y ja$

$Displaystyle y_ {i + 1} = y_ {i} + h {\ tekst {Nachylenie}} _ {\ tekst {idealny}}}$

${\ Displaystyle y_ {i + 1} = y_ {i} + {\ Frac {1}{2}}h({\text{Nachylenie}}_{\text{lewo}}+{\text{Nachylenie}}_{\text{prawo}})}$

${\ Displaystyle y_ {i + 1} = y_ { i}+{\frac {h}{2}}(f(x_{i},y_{i})+f(x_{i}+h,y_{i}+hf(x_{i},y_{ I})))}$

Dokładność metody Eulera poprawia się tylko liniowo wraz ze zmniejszaniem się wielkości kroku, podczas gdy metoda Heuna poprawia dokładność kwadratowo. Schemat można porównać z niejawną metodą trapezoidalną , ale zastąpioną przez $})}$${\ Displaystyle f (t_ {i + 1}, {\ tylda {y}} _ {i + 1})},$ aby było to wyraźne. ${\ Displaystyle {\ tylda {y}} _ {i + 1}}$ jest wynikiem jednego kroku metody Eulera na tym samym problemie z wartością początkową. Tak więc metoda Heuna jest metodą predykcyjno-korekcyjną z metodą forward Eulera jako predyktorem i metodą trapezoidalną jako korektorem.

Metoda Runge-Kutty

Ulepszona metoda Eulera jest dwuetapową metodą Runge-Kutty i można ją zapisać przy użyciu tablicy Butchera (za Johnem C. Butcherem ):

	0
	1	1
		1/2	1/2

Druga metoda określana jako metoda Heuna (znana również jako metoda Ralstona) ma stół Rzeźnika:

	0
	2/3	2/3
		1/4	3/4

Ta metoda minimalizuje błąd obcięcia.