Model autoregresyjny

W statystyce, ekonometrii i przetwarzaniu sygnałów model autoregresyjny ( AR ) jest reprezentacją pewnego rodzaju procesu losowego; jako taki jest używany do opisu pewnych zmiennych w czasie procesów w przyrodzie, ekonomii, zachowaniu itp. Model autoregresyjny określa, że ​​zmienna wyjściowa zależy liniowo od swoich własnych poprzednich wartości i od składnika stochastycznego (człon niedoskonale przewidywalny ) ; zatem model ma postać stochastycznego równania różniczkowego (lub relacji rekurencyjnej, której nie należy mylić z równaniem różniczkowym). Razem z model średniej ruchomej (MA) , jest to szczególny przypadek i kluczowy składnik bardziej ogólnych modeli autoregresji ze średnią ruchomą (ARMA) i autoregresyjnej zintegrowanej średniej ruchomej (ARIMA) szeregów czasowych, które mają bardziej skomplikowaną strukturę stochastyczną; jest to również szczególny przypadek wektorowego modelu autoregresyjnego (VAR), który składa się z systemu więcej niż jednego powiązanego stochastycznego równania różnicowego w więcej niż jednej ewoluującej zmiennej losowej.

W przeciwieństwie do modelu średniej ruchomej (MA), model autoregresyjny nie zawsze jest stacjonarny, ponieważ może zawierać pierwiastek jednostkowy.

Definicja

Notacja ${\ Displaystyle AR (p)}$ wskazuje autoregresyjny model rzędu p . Model AR( p ) jest zdefiniowany jako

${\ Displaystyle X_ {t} = \ suma _ {i = 1} ^ {p} \ varphi _ {i} X_ {ti} + \ varepsilon _{T}}$

gdzie ${\ Displaystyle \ varphi _ {1}, \ ldots, \ varphi _ {p}}$ to parametry modelu, a jest biały ${\ Displaystyle \ varepsilon _ {t}}$ hałas . Można to równoważnie zapisać za pomocą operatora przesunięcia wstecznego B as

${\ Displaystyle X_ {t} = \ suma _ {i = 1} ^ {p} \ varphi _ {i} B ^ {i} X_ { t}+\varepsilon _{t}}$

tak więc, przesuwając termin sumowania na lewą stronę i używając notacji wielomianowej , mamy

${\ Displaystyle \ phi [B] X_ {t} = \ varepsilon _ {t}}$

Model autoregresyjny można zatem postrzegać jako wynik wielobiegunowego filtru o nieskończonej odpowiedzi impulsowej , którego wejściem jest biały szum.

Niektóre ograniczenia parametrów są konieczne, aby model pozostał stacjonarny w słabym sensie. Np. procesy w modelu AR(1) z ${\ Displaystyle |\ varphi _ {1}|\ geq 1}$ nie są stacjonarne. Mówiąc bardziej ogólnie, aby model AR( p ) był stacjonarny słabo sensowny, pierwiastki wielomianu ${\ Displaystyle \ Phi (z): = \ textstyle 1- \ sum _ {i = 1} ^ {p} \ varphi _ {i} z ^ {i}} musi leżeć poza okręgiem jednostkowym$ , tj . ) korzeń ${\ displaystyle z_ {i}}$ musi spełniać ${\ Displaystyle | z_ {i} |> 1}$ (patrz strony 89,92).

Międzyokresowy efekt wstrząsów

W procesie AR jednorazowy szok wpływa na wartości ewoluującej zmiennej nieskończenie daleko w przyszłość. Rozważmy na przykład model AR (1) ${\ Displaystyle X_ {t} = \ varphi _ {1} X_ {t-1} + \ varepsilon _ {t}}$ . Niezerowa wartość dla powiedzmy czasu $t$ 1 wpływa o kwotę $}$${\ Displaystyle \ varepsilon _ {1}}$ . $} \displaystyle \varphi _{1}\varepsilon_{1}}$ równanie AR dla pod względem $wpływa$${\ Displaystyle X_ {1}}$ to o kwotę $\$ . Następnie przez równanie AR dla ${\ displaystyle X_ {3}}$ pod względem ${\ displaystyle X_ {2}}$ wpływa to na ${\ Displaystyle X_ {3}}$ o kwotę ${\ Displaystyle \ varphi _ {1} ^ {2} \ varepsilon _ {1}}$ . Kontynuacja tego procesu pokazuje , że efekt nigdy się nie kończy, chociaż jeśli proces jest $,$ efekt zmniejsza się w granicy do zera

Ponieważ każdy szok wpływa na wartości X w nieskończenie odległej przyszłości od momentu ich wystąpienia, na każdą daną wartość X _t wpływają wstrząsy występujące w nieskończenie odległej przeszłości. Można to również zobaczyć, przepisując autoregresję

${\ Displaystyle \ phi (B) X_ {t} = \ varepsilon _ {t} \,}$

(gdzie składnik stały został usunięty przez założenie, że zmienna została zmierzona jako odchylenia od jej średniej) jako

${\ Displaystyle X_ {t} = {\ Frac {1} {\ phi (B)}} \ varepsilon _ {t} \,.}$

Kiedy przeprowadzany $ma$ podział wielomianu po prawej stronie, wielomian w operatorze przesunięcia wstecz zastosowany do porządek - to znaczy nieskończoną liczbę opóźnionych wartości ${ \displaystyle \varepsilon _{t}}$ pojawiają się po prawej stronie równania.

Wielomian charakterystyczny

Funkcję autokorelacji procesu AR( p ) można wyrazić jako

$\ Displaystyle \ rho (\ tau) = \ suma _ {k = 1} ^ {p} a_ {k} y_ {k} ^ {- | \ tau |},}$

gdzie ${\ displaystyle y_ {k}}$ są pierwiastkami wielomianu

${\ Displaystyle \ phi (B) = 1- \ suma _ {k = 1} ^ {p} \ varphi _ {k} B ^ {k}}$

gdzie B jest operatorem przesunięcia wstecz $definiującą$ gdzie $jest$ funkcją autoregresję i Formuła jest ważna tylko wtedy, gdy wszystkie pierwiastki mają krotność 1.

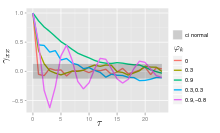
Funkcja autokorelacji procesu AR( p ) jest sumą malejących wykładników.

• Każdy rzeczywisty pierwiastek wnosi składnik do funkcji autokorelacji, który zanika wykładniczo.
• Podobnie, każda para złożonych pierwiastków sprzężonych przyczynia się do wykładniczo tłumionej oscylacji.

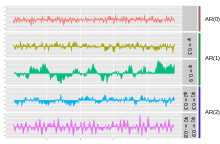
Wykresy procesów AR( p ).

AR(0); AR(1) z parametrem AR 0,3; AR(1) z parametrem AR 0,9; AR(2) z parametrami AR 0,3 i 0,3; i AR(2) z parametrami AR 0,9 i −0,8

Najprostszym procesem AR jest AR(0), w którym nie ma zależności między warunkami. Tylko składnik błędu/innowacji/szumu przyczynia się do wyniku procesu, więc na rysunku AR(0) odpowiada białemu szumowi.

W przypadku procesu AR (1) z dodatnim $tylko$ poprzedni składnik procesu i składnik szumu mają wpływ na wynik. Jeśli $\varphi$ is close to 0, then the process still looks like white noise, but as $\varphi$ approaches 1, the output gets a larger contribution from the previous term relative to the noise. This results in a "smoothing" or integration of the output, similar to a low pass filter.

W przypadku procesu AR (2) poprzednie dwa składniki i składnik szumu składają się na wynik. Jeśli zarówno i φ $\ displaystyle$$\ varphi _ {2}}$ są dodatnie, wyjście będzie przypominać filtr dolnoprzepustowy, ze zmniejszoną częścią szumu o wysokiej ${\ Displaystyle \ varphi _ {1}}$ jest dodatni, podczas gdy φ $\ Displaystyle \ varphi _ {2}}$ jest ujemna, to proces faworyzuje zmiany znaku między wyrazami procesu. Wyjście oscyluje. Można to porównać do wykrywania krawędzi lub wykrywania zmiany kierunku.

Przykład: Proces AR(1).

Proces AR(1) jest określony przez:

$${\ Displaystyle X_ {t} = \ varphi X_ {t-1} + \ varepsilon _ {t} \,}$$

gdzie $}$ procesem białego szumu z zerową średnią i stałą wariancją $\ Displaystyle \ sigma _ {\ varepsilon} ^ {2}$ . (Uwaga: indeks dolny na ${\ displaystyle \ varphi _ {1}}$ został usunięty.) Proces jest stacjonarny w sensie słabym, jeśli ${\ Displaystyle | \ varphi | <1},$ ponieważ jest uzyskiwany jako wynik stabilnego filtra, którego wejściem jest biały szum. (Jeżeli ${\ displaystyle \ varphi = 1}$ wtedy wariancja zależy od opóźnienia $sensem$ , tak że wariancja szeregu rozbiega się do nieskończoności, gdy t dąży do nieskończoności, a zatem nie jest słabym stacjonarny.) Zakładając ${\ Displaystyle |\ varphi | <1}$ , średnia jest identyczna dla wszystkich wartości t ${\ Displaystyle \ operatorname {E} (X_ {t})}$ z samej definicji stacjonarności słabego zmysłu. Jeśli średnia jest oznaczona przez $z$ wynika to

$${\ Displaystyle \ nazwa operatora {E} (X_ {t}) = \ varphi \ nazwa operatora {E} (X_ {t -1})+\nazwa_operatora {E} (\varepsilon _{t}),}$$

To

$${\ Displaystyle \ mu = \ varphi \ mu + 0,}$$

a zatem

${\ Displaystyle \ mu = 0.}$

Wariancja jest _

${\ Displaystyle {\ textrm {var}} (X_ {t}) = \ operatorname {E} (X_ { t}^{2})-\mu ^{2}={\frac {\sigma _{\varepsilon}^{2}}{1-\varphi ^{2}}},}$

gdzie jest odchyleniem standardowym $\ varepsilon _ {t}$$}$ \ Displaystyle Można to wykazać, zauważając, że

${\ Displaystyle {\ textrm {var}} (X_ {t}) = \ varphi ^ {2} {\ textrm {var}} (X_{t-1})+\sigma _{\varepsilon}^{2},}$

a następnie zauważając, że powyższa wielkość jest stałym punktem tej relacji.

Autokowariancja jest dana przez

${\ Displaystyle B_ {n} = \ nazwa operatora {E} (X_ {t + n} X_ {t}) - \ mu ^ {2} = {\ Frac {\ sigma _ {\ varepsilon} ^ {2}} 1-\varphi ^{2}}}\,\,\varphi ^{|n|}.}$

Można zauważyć, że funkcja autokowariancji zanika z czasem zaniku (zwanym także stałą czasową ) równym . ${\ Displaystyle \ tau = 1- \ varphi}$ .

Funkcja gęstości widmowej to transformata Fouriera funkcji autokowariancji. W kategoriach dyskretnych będzie to transformata Fouriera w czasie dyskretnym:

${\ Displaystyle \ Phi (\ omega) = {\ Frac {1} {\ sqrt {2 \ pi}}} \, \ suma _ {n = - \ infty} ^ {\ infty} B_ {n} e ^ { -i\omega n}={\frac {1}{\sqrt {2\pi}}}\,\left({\frac {\sigma _{\varepsilon}^{2}}{1+\varphi ^ {2}-2\varphi \cos(\omega)}}\right).}$

$okresowe ze względu na$ charakter , który przejawia jako cosinus w mianowniku. Jeśli założymy, że czas próbkowania ( $, to$$)$$mniejszy$ niż czas zaniku ( użyć przybliżenia kontinuum do $\displaystyle B_{n}}$ :

${\ Displaystyle B (t) \ około {\ Frac {\ sigma _ {\ varepsilon} ^ {2}} {1- \ varphi ^ {2}}} \, \, \ varphi ^ {| t |}}$

co daje profil Lorentza dla gęstości widmowej:

${\ Displaystyle \ Phi (\ omega) = {\ Frac {1} {\ sqrt {2 \ pi}}} \,{\frac {\sigma _{\varepsilon}^{2}}{1-\varphi ^{2}}}\,{\frac {\gamma}}{\pi (\gamma ^{2}+\ omega ^{2})}}}$

gdzie jest częstotliwością kątową związaną z czasem rozpadu $\ Displaystyle \$$gamma = 1/\ tau }$ .

φ $1$$}$${\ Displaystyle \ varphi X_ {t-2} + \ varepsilon _$ { dla równania definiującego ${\ Displaystyle X_ {t-1}} .$ Kontynuowanie tego procesu N razy daje plony

${\ Displaystyle X_ {t} = \ varphi ^ {N} X_ {tN} + \ suma _ {k = 0} ^ {N-1} \ varphi ^ {k} \ varepsilon _ {tk}.}$

Dla N zbliżającego się do nieskończoności, zbliży się do zera i: ${\ displaystyle \ varphi ^ {N}}$

${\ Displaystyle X_ {t} = \ suma _ {k = 0} ^ {\ infty} \ varphi ^ {k} \ varepsilon _ {tk}.}$

Widać, że $.$$szum$ z plus stała średnia $jest$ biały szum procesem Gaussa to $jest$ procesem Gaussa W innych przypadkach centralne twierdzenie graniczne wskazuje, że rozkład będzie w przybliżeniu normalny, gdy ${\ displaystyle X_ {t}}$${\ displaystyle \ varphi}$ jest blisko jednego.

Dla ${\ Displaystyle \ varepsilon _ {t} = 0}$ proces będzie postępem geometrycznym ( ${\ Displaystyle X_ {t} = \ varphi X_ {t-1}}$ wykładniczy wzrost lub spadek). $W$ tym przypadku rozwiązanie $:$ gdzie warunek początkowy ).

Jawna średnia/różnica postaci procesu AR(1).

Model AR(1) jest dyskretną analogią ciągłego procesu Ornsteina-Uhlenbecka . Dlatego czasami przydatne jest zrozumienie właściwości modelu AR(1) oddanego w równoważnej postaci. W tej postaci model AR (1) z parametrem procesu jest określony przez: ${\ displaystyle \ theta}$

${\ Displaystyle X_ {t + 1} = X_ {t} + (1- \ teta) (\ mu -X_ {t})+\varepsilon _{t+1}}$ , gdzie ${\ Displaystyle | \ theta | <1 \,}$ i $jest$ modelu.

Umieszczając $_$ _ szereg dla , można pokazać, że: ${\ displaystyle X_ {t + n}}$

${\ Displaystyle \ nazwa operatora {E} (X_ {t + n} | X_ {t}) = \ mu \ lewo [1-\theta ^{n}\right]+X_{t}\theta ^{n}}$ i

${\ Displaystyle \ nazwa operatora {Var} (X_ {t + n} | X_ {t}) = \ sigma ^ {2} {\ Frac {1- \ teta ^ {2n}}} {1- \ teta ^ {2}}}}$ .

Wybór maksymalnego opóźnienia

Główny artykuł: Częściowa funkcja autokorelacji

Częściowa autokorelacja procesu AR(p) jest równa zeru przy opóźnieniach większych niż p, więc odpowiednie maksymalne opóźnienie p to takie, po którym wszystkie autokorelacje częściowe wynoszą zero.

Obliczanie parametrów AR

Istnieje wiele sposobów szacowania współczynników, takich jak zwykła procedura najmniejszych kwadratów lub metoda momentów (poprzez równania Yule-Walkera).

AR( p ) jest określony równaniem

${\ Displaystyle X_ {t} = \ suma _ {i = 1} ^ {p} \ varphi _ {i} X_ {ti} + \ varepsilon _ {t}. \,}$

Opiera się na parametrach, $.$ = 1 , ..., p Istnieje bezpośrednia zgodność między tymi parametrami a funkcją kowariancji procesu, a tę zgodność można odwrócić, aby określić parametry z funkcji autokorelacji (która sama jest uzyskiwana z kowariancji). Odbywa się to za pomocą równań Yule-Walkera.

Równania Yule-Walkera

Równania Yule-Walkera, nazwane na cześć Udny Yule i Gilberta Walkera , to następujący zestaw równań.

${\ Displaystyle \ gamma _ {m} = \ suma _ {k = 1} ^ {p} \ varphi _ {k} \gamma _{mk}+\sigma _{\varepsilon}^{2}\delta _{m,0},}$

gdzie m = 0, …, p , dając równania p + 1 . Tutaj jest funkcją autokowariancji X $Displaystyle$ σ $\ sigma _ {\ varepsilon}}$ jest odchyleniem standardowym procesu szumu wejściowego i _δ $\ displaystyle \delta _{m,0}}$ to funkcja delta Kroneckera .

Ponieważ ostatnia część pojedynczego równania jest różna od zera tylko wtedy, gdy m = 0 , układ równań można rozwiązać, przedstawiając równania dla m > 0 w postaci macierzowej, otrzymując w ten sposób równanie

${\ Displaystyle {\ rozpocząć {bmatrix} \ gamma _ {1} \\\ gamma _ {2} \\\ gamma _ {3} \\\ vdots \\\ gamma _ {p}\\\end{bmatrix}}={\begin{bmatrix}\gamma _{0}&\gamma _{-1}&\gamma _{-2}&\cdots \\\gamma _{1 }&\gamma _{0}&\gamma _{-1}&\cdots \\\gamma _{2}&\gamma _{1}&\gamma _{0}&\cdots \\\vdots &\ vdots &\vdots &\ddots \\\gamma _{p-1}&\gamma _{p-2}&\gamma _{p-3}&\cdots \\\end{bmatrix}}{\begin{ bmatrix}\varphi _{1}\\\varphi _{2}\\\varphi _{3}\\\vdots \\\varphi _{p}\\\end{bmatrix}}}$

które można rozwiązać dla wszystkich ${\ Displaystyle \ {\ varphi _ {m}; m = 1,2, \ kropki, p \}.$ Pozostałe równanie dla m = 0 to

${\ Displaystyle \ gamma _ {0} = \ suma _ {k = 1} ^ {p} \ varphi _ {k} \ gamma _ {- k}+\sigma _{\varepsilon}^{2},}$

co raz ${\ Displaystyle \ {\ varphi _ {m}; m = 1,2, \ kropki, p \}}$ są znane, można je rozwiązać dla ${\ Displaystyle \ sigma _ {\ varepsilon} ^ {2}.}$

Alternatywne sformułowanie dotyczy funkcji autokorelacji . $p$ przez pierwsze elementy funkcji autokorelacji + 1 Pełną funkcję autokorelacji można następnie wyprowadzić przez obliczenia rekurencyjne

${\ Displaystyle \ rho (\ tau) = \ suma _ {k = 1} ^ {p} \ varphi _ {k} \ rho (k -\tau )}$

procesów AR( p ) niskiego rzędu

• p = 1
  • ${\ Displaystyle \ gamma _ {1} = \ varphi _ {1} \ gamma _ {0}}$
  • Stąd ${\ Displaystyle \ rho _ {1} = \ gamma _ {1} / \ gamma _ {0} = \ varphi _ {1}}$
• p = 2
  • Równania Yule-Walkera dla procesu AR (2) to

    ${\ Displaystyle \ gamma _ {1} = \ varphi _ {1} \ gamma _ {0} + \ varphi _ {2} \ gamma _ {-1}}$

    ${\ Displaystyle \ gamma _ {2} = \ varphi _ {1} \ gamma _ {1} + \ varphi _ { 2}\gamma_{0}}$

    • Pamiętaj, że ${\ Displaystyle \ gamma _ {-k} = \ gamma _ {k}}$
    • Korzystanie z pierwszego równania daje ${\ Displaystyle \ rho _ {1} = \ gamma _ {1} / \ gamma _ {0} = {\ Frac {\ varphi _ {1}}{1-\varphi_{2}}}}$
    • Korzystanie ze wzoru rekurencji daje ${\ Displaystyle \ rho _ {2} = \ gamma _ {2} / \ gamma _ {0} ={\frac {\varphi _{1}^{2}-\varphi _{2}^{2}+\varphi _{2}}{1-\varphi _{2}}}}$

Estymacja parametrów AR

Powyższe równania (równania Yule-Walkera) zapewniają kilka dróg do oszacowania parametrów modelu AR( p ), poprzez zastąpienie kowariancji teoretycznych wartościami szacunkowymi. Niektóre z tych wariantów można opisać w następujący sposób:

• Estymacja autokowariancji lub autokorelacji. Tutaj każdy z tych terminów jest szacowany osobno, przy użyciu konwencjonalnych szacunków. Można to zrobić na różne sposoby, a wybór między nimi wpływa na właściwości schematu estymacji. Na przykład ujemne oszacowania wariancji mogą być generowane przez niektóre wybory.
• Sformułowanie jako problem regresji metodą najmniejszych kwadratów , w którym konstruuje się zwykły problem predykcji metodą najmniejszych kwadratów, opierając predykcję wartości X _t na p poprzednich wartościach tego samego szeregu. Można to traktować jako schemat przewidywania przyszłości. normalne równania tego problemu odpowiadają przybliżeniu postaci macierzowej równań Yule-Walkera, w których każde pojawienie się autokowariancji tego samego opóźnienia jest zastępowane przez nieco inne oszacowanie.
• Sformułowanie jako rozszerzona postać zwykłego problemu przewidywania metodą najmniejszych kwadratów. Tutaj dwa zestawy równań predykcyjnych są łączone w jeden schemat estymacji i jeden zestaw równań normalnych. Jeden zestaw to zestaw równań predykcji do przodu, a drugi to odpowiedni zestaw równań predykcji wstecznej, odnoszący się do reprezentacji wstecznej modelu AR:

${\ Displaystyle X_ {t} = \ suma _ {i = 1} ^ {p} \ varphi _ {i} X_ {ti} + \ varepsilon _ {t} ^ {*} \,.} Tutaj przewidywane$

wartości X _t byłoby oparte na przyszłych wartościach p tego samego szeregu. Ten sposób szacowania parametrów AR pochodzi od Burga i jest nazywany metodą Burga: Burg i późniejsi autorzy nazwali te konkretne oszacowania „oszacowaniami maksymalnej entropii”, ale uzasadnienie tego dotyczy zastosowania dowolnego zestawu oszacowanych parametrów AR. W porównaniu ze schematem estymacji wykorzystującym tylko równania predykcji do przodu, tworzone są różne oszacowania autokowariancji, a oszacowania mają różne właściwości stabilności. Szacunki Burga są szczególnie związane z estymacją widmową maksymalnej entropii .

Inne możliwe podejścia do szacowania obejmują oszacowanie maksymalnego prawdopodobieństwa . Dostępne są dwa różne warianty maksymalnego prawdopodobieństwa: w jednym (w przybliżeniu równoważnym ze schematem najmniejszych kwadratów przewidywania w przód) rozważana funkcja wiarygodności odpowiada rozkładowi warunkowemu późniejszych wartości w szeregu, biorąc pod uwagę początkowe p wartości w szeregu; w drugim rozważana funkcja wiarygodności odpowiada bezwarunkowemu łącznemu rozkładowi wszystkich wartości w obserwowanym szeregu. Istotne różnice w wynikach tych podejść mogą wystąpić, jeśli obserwowany szereg jest krótki lub gdy proces jest bliski niestacjonarności.

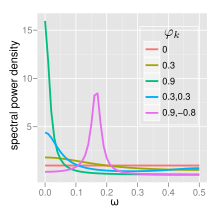
Widmo

Gęstość widmowa mocy (PSD) procesu AR ( p ) z wariancją szumu ${\ Displaystyle \ operatorname {Var} (Z_ {t}) = \ sigma _ {Z} ^ {2}}$ jest

${\ Displaystyle S (f) = {\ Frac {\ sigma _ {Z} ^ {2}} {| 1- \ suma _ {k = 1} ^ {p} \ varphi _ {k} e ^ {-i2 \pi fk}|^{2}}}.}$

AR(0)

Dla białego szumu (AR(0))

${\ Displaystyle S (f) = \ sigma _ {Z} ^ {2}.}$

AR(1)

Dla AR(1)

${\ Displaystyle S (f) = {\ Frac {\ sigma _ {Z} ^ {2}} {| 1- \ varphi _ { 1}e^{-2\pi if}|^{2}}}={\frac {\sigma _{Z}^{2}}{1+\varphi _{1}^{2}-2\ varphi _{1}\cos 2\pi f}}}$

• Jeśli istnieje pojedynczy pik widmowy przy f = 0 $,$ szumem . Gdy $1$ , przy niskich częstotliwościach jest większa moc, tj. większe opóźnienia Jest to filtr dolnoprzepustowy, po zastosowaniu do światła o pełnym spektrum wszystko oprócz światła czerwonego zostanie przefiltrowane.
• Jeśli $jako$ minimum przy f = 0, często szum . To podobnie działa jak filtr górnoprzepustowy, wszystko oprócz niebieskiego światła zostanie przefiltrowane.

AR(2)

Procesy AR(2) można podzielić na trzy grupy w zależności od charakterystyki ich korzeni:

${\ Displaystyle z_ {1}, z_ {2} = - {\ Frac {1} {2 \ varphi _ {2} }}}\left(\varphi _{1}\pm {\sqrt {\varphi _{1}^{2}+4\varphi _{2}}}\right)}$

• Gdy ${\ Displaystyle \ varphi _ {1} ^ {2} + 4 \ varphi _ {2}<0}$ , proces ma parę zespolonych korzeni, tworząc szczyt średniej częstotliwości w:

${\ Displaystyle f ^ {* }={\frac {1}{2\pi}}\cos ^{-1}\left({\frac {\varphi _{1}(\varphi _{2}-1)}{4\varphi _ {2}}}\prawo)}$

W przeciwnym razie proces ma rzeczywiste korzenie i:

• Gdy działa jako filtr dolnoprzepustowy białego szumu z pikiem widmowym przy $\varphi _{1}>0$$\ Displaystyle \ varphi _ {1}>$
• Kiedy działa $1/2$$/$ 2 }

Proces jest niestacjonarny, gdy pierwiastki znajdują się poza okręgiem jednostkowym. Proces jest stabilny, gdy pierwiastki mieszczą się w okręgu jednostkowym lub równoważnie, gdy współczynniki znajdują się w trójkącie ${\ Displaystyle -1 \ równoważnik \ varphi _ {2} \ równoważnik 1- | \ varphi _ {1} |}$ .

Pełną funkcję PSD można wyrazić w postaci rzeczywistej jako:

${\ Displaystyle S (f) = {\ Frac {\ sigma _ {Z} ^ {2}} {1+ \ varphi _ {1} ^ {2} + \ varphi _ {2} ^ {2} -2 \ varphi _{1}(1-\varphi _{2})\cos(2\pi f)-2\varphi _{2}\cos(4\pi f)}}}$

Implementacje w pakietach statystycznych

• R , pakiet statystyk zawiera funkcję ar .
• MATLAB zawiera modele autoregresyjne
• Matlab i Octave : zestaw narzędzi TSA zawiera kilka funkcji estymacji dla jednowymiarowych, wielowymiarowych i adaptacyjnych modeli autoregresyjnych.
• PyMC3 : statystyki bayesowskie i ramy programowania probabilistycznego obsługują tryby autoregresji z opóźnieniami .
• Bayesloop obsługuje wnioskowanie o parametrach i wybór modelu dla procesu AR-1 z parametrami zmieniającymi się w czasie.
• Python : implementacja w statsmodels.

Odpowiedź impulsowa

Odpowiedź impulsowa systemu to zmiana ewoluującej zmiennej w odpowiedzi na zmianę wartości składnika szoku k okresów wcześniej, jako funkcję k . Ponieważ model AR jest szczególnym przypadkiem modelu wektorowej autoregresji, zastosowanie ma tutaj obliczenie odpowiedzi impulsowej w wektorze autoregresja#odpowiedź impulsowa .

n – prognozowanie krok do przodu

Raz parametry autoregresji

${\ Displaystyle X_ {t} = \ suma _ {i = 1} ^ {p} \ varphi _ {i} X_ {ti} + \ varepsilon _{T}\,}$

zostały oszacowane, autoregresja może być wykorzystana do prognozowania dowolnej liczby okresów w przyszłości. Pierwsze użycie t odnosi się do pierwszego okresu, dla którego dane nie są jeszcze dostępne; zastąp znane poprzednie wartości X _t-i dla i = 1, ..., p do równania $autoregresyjnego$ , ustawiając składnik błędu (ponieważ prognozujemy X _t równa się jego wartości oczekiwanej, a wartość oczekiwana składnika błędu nieobserwowanego wynosi zero). Wynikiem równania autoregresyjnego jest prognoza dla pierwszego nieobserwowanego okresu. Następnie użyj t , aby odnieść się do następnego okresu, dla którego dane nie są jeszcze dostępne; ponownie równanie autoregresyjne jest używane do prognozy, z jedną różnicą: wartością X jeden okres poprzedzający obecnie prognozowany okres nie jest znany, dlatego zamiast tego używana jest jego wartość oczekiwana — przewidywana wartość wynikająca z poprzedniego etapu prognozowania. Następnie dla przyszłych okresów stosuje się tę samą procedurę, za każdym razem wykorzystując jedną wartość prognozy więcej po prawej stronie równania predykcyjnego, aż po p wszystkie wartości p po prawej stronie są przewidywanymi wartościami z poprzednich kroków.

Istnieją cztery źródła niepewności dotyczące otrzymanych w ten sposób predykcji: (1) niepewność co do tego, czy model autoregresyjny jest modelem poprawnym; (2) niepewność co do dokładności prognozowanych wartości, które są używane jako wartości opóźnione po prawej stronie równania autoregresyjnego; (3) niepewność co do prawdziwych wartości współczynników autoregresji; $.$ (4) niepewność co do wartości składnika błędu przewidywanego okresu Każdy z trzech ostatnich można określić ilościowo i połączyć, aby uzyskać przedział ufności dla n -prognozy wyprzedzające; przedział ufności będzie się poszerzał wraz ze n ze względu na stosowanie coraz większej liczby oszacowanych wartości dla zmiennych po prawej stronie.

Ocena jakości prognoz

Wydajność predykcyjną modelu autoregresyjnego można ocenić natychmiast po przeprowadzeniu estymacji, jeśli stosowana jest walidacja krzyżowa . W tym podejściu niektóre z początkowo dostępnych danych wykorzystano do celów oszacowania parametrów, a niektóre (z dostępnych później obserwacji w zbiorze danych) wstrzymano do testów poza próbą. Alternatywnie, po pewnym czasie od przeprowadzenia estymacji parametrów, dostępnych będzie więcej danych i wówczas można będzie ocenić wydajność predykcyjną przy użyciu nowych danych.

W obu przypadkach można ocenić dwa aspekty wydajności predykcyjnej: wydajność o jeden krok do przodu i n - wydajność o krok do przodu. W przypadku wydajności o jeden krok do przodu oszacowane parametry są używane w równaniu autoregresyjnym wraz z obserwowanymi wartościami X dla wszystkich okresów poprzedzających ten, który jest przewidywany, a wynikiem równania jest prognoza o jeden krok do przodu; procedura ta służy do uzyskiwania prognoz dla każdej z obserwacji poza próbą. Aby ocenić jakość n -krokowych do przodu, stosuje się procedurę prognozowania opisaną w poprzedniej sekcji w celu uzyskania prognoz.

Biorąc pod uwagę zestaw przewidywanych wartości i odpowiadający im zestaw rzeczywistych wartości dla X dla różnych okresów, powszechną techniką oceny jest użycie średniokwadratowego błędu prognozy ; dostępne są również inne miary (patrz prognozowanie#dokładność prognozowania ).

Powstaje pytanie, jak interpretować zmierzoną dokładność prognozowania - na przykład, jaka jest „wysoka” (zła) lub „niska” (dobra) wartość średniego kwadratowego błędu prognozy? Istnieją dwa możliwe punkty porównania. Po pierwsze, do celów porównawczych można wykorzystać dokładność prognoz modelu alternatywnego, oszacowaną przy różnych założeniach modelowania lub przy użyciu różnych technik szacowania. Po drugie, miarę dokładności poza próbą można porównać z tą samą miarą obliczoną dla punktów danych w próbce (które zostały użyte do oszacowania parametrów), dla których dostępna jest wystarczająca liczba wcześniejszych wartości danych (tj . punkty danych, dla których p wcześniejszych punktów danych nie jest dostępnych). Ponieważ model został oszacowany tak, aby jak najlepiej pasował do punktów w próbce, zwykle będzie tak, że wydajność predykcyjna poza próbą będzie gorsza niż wydajność predykcyjna w próbie. Ale jeśli jakość predykcyjna pogorszy się poza próbą o „niewiele” (co nie jest dokładnie definiowalne), wówczas prognosta może być zadowolony z wyników.

Zobacz też

• Model średniej ruchomej
• Równanie różnicowe liniowe
• Analityka predykcyjna
• Liniowe kodowanie predykcyjne
• Rezonans
• Rekurencja Levinsona
• Proces Ornsteina-Uhlenbecka

Notatki

•   Mills, Terence C. (1990). Techniki szeregów czasowych dla ekonomistów . Wydawnictwo Uniwersytetu Cambridge. ISBN 9780521343398 .
• Percival, Donald B.; Walden, Andrew T. (1993). Analiza widmowa do zastosowań fizycznych . Wydawnictwo Uniwersytetu Cambridge. Bibcode : 1993sapa.book.....P .
• Pandit, Sudhakar M.; Wu, Shien-Ming (1983). Analiza szeregów czasowych i systemów z aplikacjami . John Wiley & Synowie.

Linki zewnętrzne

• Analiza autoregresji (AR) autorstwa Paula Bourke
• na YouTube autorstwa Marka Thomy