Modelowanie numeryczne (geologia)

Symulacja propagacji fali sejsmicznej w skali globalnej z wykorzystaniem superkomputera do rozwiązywania równań falowych

W geologii modelowanie numeryczne jest szeroko stosowaną techniką rozwiązywania złożonych problemów geologicznych poprzez symulację obliczeniową scenariuszy geologicznych .

Modelowanie numeryczne wykorzystuje modele matematyczne do opisu warunków fizycznych scenariuszy geologicznych za pomocą liczb i równań. Niemniej jednak niektóre z ich równań są trudne do bezpośredniego rozwiązania, na przykład równania różniczkowe cząstkowe . Dzięki modelom numerycznym geolodzy mogą stosować metody, takie jak metody różnic skończonych , aby przybliżyć rozwiązania tych równań. Na tych modelach można następnie przeprowadzać eksperymenty numeryczne, uzyskując wyniki, które można interpretować w kontekście procesu geologicznego. Dzięki tym eksperymentom można rozwinąć zarówno jakościowe, jak i ilościowe zrozumienie różnych procesów geologicznych.

Modelowanie numeryczne zostało wykorzystane do badania mechaniki skał , historii termicznej skał, ruchów płyt tektonicznych i płaszcza Ziemi. Przepływ płynów jest symulowany za pomocą metod numerycznych, co pokazuje, w jaki sposób wody gruntowe lub w jaki sposób ruchy stopionego rdzenia zewnętrznego wytwarzają pole geomagnetyczne.

Historia

Przed rozwojem modelowania numerycznego modelowanie analogowe , które symuluje naturę przy zmniejszonej skali masy, długości i czasu, było jednym z głównych sposobów rozwiązywania problemów geologicznych, na przykład modelowania formowania się pasów oporowych . Proste analityczne lub półanalityczne modele matematyczne były również używane do ilościowego rozwiązywania stosunkowo prostych problemów geologicznych.

Od późnych lat 60. do 70. XX wieku, po opracowaniu metod elementów skończonych w rozwiązywaniu problemów mechaniki ośrodków ciągłych w inżynierii lądowej , metody numeryczne zostały zaadaptowane do modelowania złożonych zjawisk geologicznych, na przykład fałdowania i konwekcji płaszcza . Wraz z postępem technologii komputerowej poprawiła się dokładność modeli numerycznych. Modelowanie numeryczne stało się ważnym narzędziem rozwiązywania problemów geologicznych, zwłaszcza w przypadku tych części Ziemi, które trudno jest bezpośrednio obserwować, takich jak płaszcz i rdzeń . Jednak modelowanie analogowe jest nadal przydatne w modelowaniu scenariuszy geologicznych, które trudno uchwycić w modelach numerycznych, a połączenie modelowania analogowego i numerycznego może być przydatne do lepszego zrozumienia procesów zachodzących na Ziemi.

składniki

Etapy modelowania numerycznego. Pierwszym krokiem w modelowaniu numerycznym jest ilościowe uchwycenie rzeczywistego scenariusza geologicznego. Na przykład w modelowaniu konwekcji płaszcza równania ciepła są używane do opisania energii cieplnej krążącej w układzie, podczas gdy równania Naviera-Stokesa opisują przepływ lepkiej cieczy (skały płaszcza). Po drugie, ponieważ równania te są trudne do rozwiązania, dyskretyzacja a metody numeryczne są wybierane w celu przybliżenia równań rządzących. Następnie algorytmy w komputerze mogą obliczyć przybliżone rozwiązania. Wreszcie z tych rozwiązań można dokonać interpretacji. Na przykład w modelowaniu konwekcyjnym płaszcza można najpierw zwizualizować przepływ płaszcza. Następnie można wnioskować o zależności między wzorcami przepływu a parametrami wejściowymi.

Ogólne badanie modelu numerycznego składa się zwykle z następujących elementów:

Model matematyczny to uproszczony opis problemu geologicznego, taki jak równania i warunki brzegowe. Te równania rządzące modelem są często równaniami różniczkowymi cząstkowymi , które są trudne do bezpośredniego rozwiązania, ponieważ obejmuje pochodną funkcji , na przykład równanie falowe .
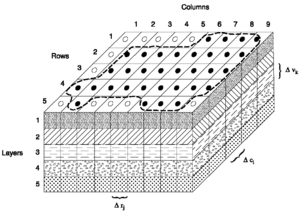
Metody dyskretyzacji i metody numeryczne przekształcają równania rządzące modelami matematycznymi w równania dyskretne. Te dyskretne równania mogą przybliżać rozwiązanie równań rządzących. Typowe metody obejmują metodę elementu skończonego , różnicę skończoną lub metodę skończonej objętości , które dzielą przedmiot zainteresowania na mniejsze części (element) za pomocą siatki. Te dyskretne równania można następnie rozwiązać numerycznie w każdym elemencie. Metoda elementów dyskretnych wykorzystuje inne podejście, ta metoda polega na ponownym złożeniu obiektu zainteresowania z wielu drobnych cząstek. Następnie do interakcji między cząstkami stosuje się proste równania rządzące.
Algorytmy to programy komputerowe, które obliczają rozwiązanie, wykorzystując ideę powyższych metod numerycznych.
Interpretacji dokonuje się na podstawie rozwiązań podanych w modelach numerycznych.

Nieruchomości

Dobry model numeryczny ma zwykle niektóre z następujących właściwości:

Spójny : Modele numeryczne często dzielą obiekt na mniejsze elementy. Jeśli model jest spójny, wynik modelu numerycznego jest prawie taki sam, jak przewiduje model matematyczny, gdy rozmiar elementu jest bliski zeru. Innymi słowy, błąd między równaniami dyskretnymi zastosowanymi w modelu numerycznym a równaniami rządzącymi w modelu matematycznym dąży do zera, gdy przestrzeń siatki (rozmiar elementu) zbliża się do zera.
Stabilny : W stabilnym modelu numerycznym błąd podczas obliczeń metodami numerycznymi nie zwiększa się. Błąd niestabilnego modelu szybko się kumuluje i prowadzi do nieprawidłowego wyniku. Stabilny i spójny model numeryczny daje takie same wyniki, jak dokładne rozwiązanie w modelu matematycznym , gdy rozstaw oczek (rozmiar elementu) jest bardzo mały.
Zbieżność : Dane wyjściowe modelu numerycznego są bliższe faktycznemu rozwiązaniu rządzących równań w modelach matematycznych, gdy zmniejsza się rozstaw oczek (rozmiar elementu), co zwykle sprawdza się przeprowadzając eksperymenty numeryczne.
Zachowane : Wielkości fizyczne w modelach, takie jak masa i pęd, są zachowane. Ponieważ równania w modelach matematycznych są zwykle wyprowadzane z różnych praw zachowania, wynik modelu nie powinien naruszać tych przesłanek.
Ograniczony : Rozwiązanie podane przez model numeryczny ma rozsądne ograniczenia fizyczne w odniesieniu do modeli matematycznych, na przykład masa i objętość powinny być dodatnie.
Dokładne : rozwiązanie podane przez modele numeryczne jest zbliżone do rzeczywistego rozwiązania przewidywanego przez model matematyczny.

Obliczenie

Poniżej przedstawiono niektóre kluczowe aspekty pomysłów w opracowywaniu modeli numerycznych w geologii. Najpierw należy ustalić sposób opisu obiektu i ruchu ( kinematyczny ). Następnie zapisywane są równania opisujące problemy geologiczne, na przykład równania cieplne opisują przepływ ciepła w systemie. Ponieważ niektórych z tych równań nie można rozwiązać bezpośrednio, do przybliżenia rozwiązania rządzących równań stosuje się metody numeryczne.

Opisy kinematyczne

W modelach numerycznych i modelach matematycznych istnieją dwa różne podejścia do opisu ruchu materii: eulerowskie i lagranżowskie . W geologii oba podejścia są powszechnie stosowane do modelowania przepływu płynów, takiego jak konwekcja płaszcza, gdzie do obliczeń używana jest siatka Eulera, a do wizualizacji ruchu używane są znaczniki Lagrange'a. Ostatnio pojawiły się modele, które próbują opisać różne części przy użyciu różnych podejść, aby połączyć zalety tych dwóch podejść. To połączone podejście nazywa się arbitralnym podejściem Lagrange'a-Eulera .

eulerowski

Podejście Eulera uwzględnia zmiany wielkości fizycznych, takich jak masa i prędkość, w ustalonym miejscu w czasie. Jest to podobne do obserwowania, jak woda w rzece przepływa przez most. Matematycznie wielkości fizyczne można wyrazić jako funkcję lokalizacji i czasu. To podejście jest przydatne w przypadku płynnych i jednorodnych (jednolitych) materiałów, które nie mają naturalnej granicy.

Lagrange'a

Z drugiej strony podejście Lagrange'a uwzględnia zmianę wielkości fizycznych, takich jak objętość, stałych elementów materii w czasie. Jest to podobne do patrzenia na pewien zbiór cząsteczek wody płynących w dół rzeki. Korzystając z podejścia Lagrange'a, łatwiej jest śledzić obiekty stałe, które mają naturalną granicę oddzielającą je od otoczenia.

Opisy kinematyczne

Podejście Eulera Na rysunku pomarańczowa ramka wskazuje obszar zainteresowania. W podejściu Eulera położenie czerwonego prostokąta jest ustalone, podczas gdy zmiana koloru tego prostokąta ilustruje zmieniającą się wartość w tym położeniu.
Podejście Lagrange'a. Na rysunku pomarańczowa ramka wskazuje obszar zainteresowania. W podejściu Lagrange'a położenie czerwonego prostokąta nie jest stałe, przesuwa się w czasie. Obszarem zainteresowania jest zawsze ten sam element.

Równania rządzące

Poniżej przedstawiono kilka podstawowych równań, które są powszechnie używane do opisywania zjawisk fizycznych, na przykład, jak materia w systemie geologicznym porusza się lub przepływa i jak energia cieplna jest rozprowadzana w systemie. Te równania są zwykle rdzeniem modelu matematycznego.

Równanie ciągłości

Równanie ciągłości jest matematyczną wersją stwierdzenia, że obiekt lub ośrodek geologiczny jest ciągły, co oznacza, że w obiekcie nie można znaleźć pustej przestrzeni. Równanie to jest powszechnie stosowane w modelowaniu numerycznym w geologii.

Jednym z przykładów jest równanie ciągłości masy płynu. ${\ displaystyle$ się na prawie zachowania masy , dla płynu o gęstości $}$ pozycji w ustalonej objętości płynu, szybkość zmian jest $rho$ masa jest równa zewnętrznemu przepływowi płynu przez granicę : ${\ displaystyle S}: S {\ displaystyle S}$

${\ Displaystyle {\ Frac {\ częściowy} {\ częściowy t}} \ int \ granice _ {V} \ rho d \ tau = - \ int \limits_{S}\rho u_{j}dS_{j}}$

gdzie $}$ elementem objętości i $jest$ prędkością w $displaystyle \$ .

W postaci Lagrange'a:

${\ Displaystyle {\ Frac {D \ rho} {Dt}} \ równoważnik {\ Frac {\ częściowy \ rho }{\częściowe t}}+u_{j}{\frac {\częściowe \rho }{\częściowe x_{j}}}=-\rho {\frac {\częściowe u_{j}}{\częściowe x_ {J}}}}$

W postaci Eulera:

${\ Displaystyle {\ Frac {\ częściowy \ rho} {\ częściowy t}} = {\ Frac {\ częściowy (\ rho u_ {j})} {\ częściowe x_{j}}}}$

To równanie jest przydatne, gdy model obejmuje ciągły przepływ płynu, na przykład płaszcz w geologicznych skalach czasu.

Równanie pędu

Równanie pędu opisuje, w jaki sposób materia porusza się w odpowiedzi na przyłożoną siłę. Jest to wyrażenie drugiej zasady dynamiki Newtona .

Rozważ stałą $objętość$ . Zgodnie z zasadą zachowania pędu tempo zmiany objętości jest równe:

$przyłożona$ zewnętrzna do elementu
$przyłożone$ do powierzchni element
minus pęd wychodzący z elementu na tej powierzchni

${\ częściowy}} {\ częściowe t}}\int \limits _{V}\rho u_{i}d\tau =\int \limits _{V}\rho F_{i}d\tau +\int \limits _{S}\sigma _{ij}dS_{j}-\int \limits _{S}\rho u_{i}u_{j}dS_{j}}$

gdzie $jest$ elementem objętości, $u$ .

Po uproszczeniach i integracjach, dla dowolnego tomu , postać Eulera tego równania to: ${\ displaystyle V}$

$\ rho {\ Frac {\ częściowe u_ {i}} {\ częściowe t}} +\rho u_{j}{\frac {\częściowe u_{i}}{\częściowe x_{j}}}=\rho F_{i}+{\frac {\częściowe \sigma _{ij}}{\ częściowe x_{j}}}}$

Równanie ciepła

Równania ciepła opisują, w jaki sposób energia cieplna przepływa w systemie.

Z zasady zachowania energii wynika, że szybkość zmiany energii stałej objętości $displaystyle$ jest równa: mi { $E}$

praca wykonana na granicy ${\ displaystyle S}$
plus praca wykonana przez siłę zewnętrzną w objętości $\ displaystyle F$ $}$
przewodnictwo cieplne przez granicę ${\ displaystyle S}$
minus konwekcja ciepła przez granicę ${\ Displaystyle S}$
plus ciepło wytwarzane wewnętrznie

Matematycznie:

${\ Displaystyle {\ Frac {\ częściowy}} {\ częściowy t}} \ int \ granice _ {V} \ rho Ed \ tau = \ int \ granice _ {S} u_ {i} \ sigma _{ij}dS_{j}+\int \limits _{V}\rho u_{i}F_{i}d\tau -\int \limits _{S}k{\frac {\częściowe T}{\ częściowe x_{j}}}dS_{j}-\int \limits_{S}\rho Eu_{j}dS_{j}+\int \limits_{V}\rho Hd\tau }$

gdzie ${\ Displaystyle \ tau}$ $}$ $jest$ objętości, jest prędkością, $temperaturą$ , jest współczynnikiem przewodzenia i ${\ Displaystyle$ to szybkość produkcji ciepła.

Metody numeryczne

Przykład siatki elementów skończonych 2D. Domena jest podzielona na liczne nienakładające się na siebie trójkąty (elementy). Węzły to wierzchołki trójkątów.

Metody numeryczne to techniki przybliżania równań rządzących w modelach matematycznych.

Powszechne metody numeryczne obejmują metodę elementów skończonych , metodę widmową , metodę różnic skończonych i metodę objętości skończonych . Metody te służą do aproksymacji rozwiązania rządzących równaniami różniczkowymi w modelu matematycznym poprzez podzielenie domeny na siatki lub siatki i zastosowanie prostszych równań do poszczególnych elementów lub węzłów w siatce.

Aproksymacja równań falowych metodą elementów skończonych. Domena jest podzielona na liczne trójkąty. Obliczane są wartości węzłów w siatce, pokazujące, jak fala rozchodzi się w regionie.

Metoda elementów dyskretnych wykorzystuje inne podejście. Obiekt jest uważany za zbiór małych cząstek.

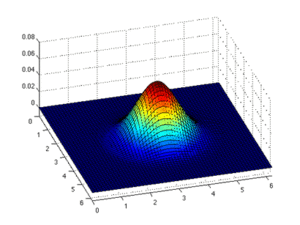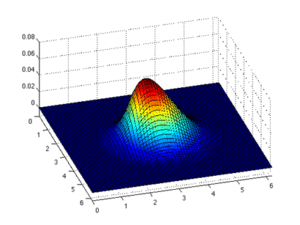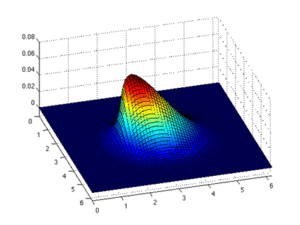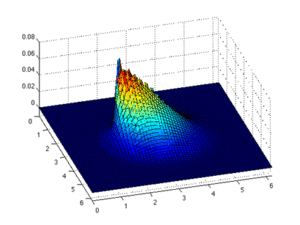
Metoda elementów skończonych

Metoda elementów skończonych dzieli obiekt (lub domenę) na mniejsze, nienakładające się na siebie elementy (lub subdomeny), które są połączone w węzłach. Rozwiązanie równań różniczkowych cząstkowych jest następnie aproksymowane prostszymi równaniami elementarnymi, zwykle wielomianami . Następnie te równania elementów są łączone w równania dla całego obiektu, tj. wkład każdego elementu jest sumowany w celu modelowania odpowiedzi całego obiektu. Ta metoda jest powszechnie stosowana do rozwiązywania problemów mechanicznych. Poniżej przedstawiono ogólne kroki korzystania z metody elementów skończonych:

Wybierz typ elementu i podziel obiekt. Typowe typy elementów to trójkątne, czworoboczne, czworościenne itp. Do różnych problemów należy wybierać różne typy elementów.
Zdecyduj funkcję przemieszczenia. Funkcja przemieszczenia określa sposób poruszania się elementów. Powszechnie stosowane są funkcje wielomianowe liniowe, kwadratowe lub sześcienne .
Zdecyduj zależność przemieszczenie-odkształcenie. Przemieszczenie elementu zmienia lub deformuje kształt elementu, co technicznie nazywa się odkształceniem . Zależność ta oblicza, jak duże odkształcenie elementu zostało doznane w wyniku przemieszczenia.
Zdecyduj zależność odkształcenie-naprężenie. Odkształcenie elementu powoduje naprężenie elementu, które jest siłą przyłożoną do elementu. Ta zależność oblicza wielkość naprężenia doświadczanego przez element z powodu odkształcenia. Jednym z przykładów tej relacji jest prawo Hooke'a .
Wyprowadzić równania sztywności i macierz sztywności dla elementów. Naprężenie powoduje również odkształcenie elementu; sztywność (sztywność) elementów wskazuje, jak bardzo odkształcą się one w odpowiedzi na naprężenia . Sztywność elementów w różnych kierunkach jest przedstawiona w postaci macierzy dla uproszczenia operacji podczas obliczeń.
Połącz równania elementów w równania globalne. Wkłady każdego elementu są sumowane do zestawu równań opisujących cały system.
Zastosuj warunki brzegowe. Predefiniowane warunki na granicy, takie jak temperatura, naprężenia i inne wielkości fizyczne są wprowadzane na granicę systemu.
Rozwiąż dla przemieszczenia. W miarę upływu czasu przemieszczenie elementów jest rozwiązywane krok po kroku.
Rozwiązanie problemu napięć i stresu. Po obliczeniu przemieszczenia odkształcenia i naprężenia są obliczane przy użyciu relacji w krokach 3 i 4.

Rozwiązanie równania Burgersa opisującego zachowanie się fal uderzeniowych metodą spektralną . Domena jest najpierw dzielona na prostokątną siatkę. Idea tej metody jest podobna do metody elementów skończonych.

Metoda spektralna

Metoda widmowa jest podobna do metody elementów skończonych. Główna różnica polega na tym, że metoda spektralna wykorzystuje funkcje bazowe , prawdopodobnie za pomocą szybkiej transformacji Fouriera (FFT) , która przybliża funkcję przez sumę wielu prostych funkcji. Tego rodzaju funkcje bazowe można następnie zastosować do całej dziedziny i przybliżyć rządzące równania różniczkowe cząstkowe . Dlatego każde obliczenie bierze pod uwagę informacje z całej dziedziny, podczas gdy metoda elementów skończonych bierze pod uwagę tylko informacje z sąsiedztwa. W rezultacie metoda spektralna jest zbieżna wykładniczo i nadaje się do rozwiązywania problemów o dużej zmienności w czasie lub przestrzeni.

Metoda objętości skończonej

Metoda objętości skończonych jest również podobna do metody elementów skończonych. Dzieli również obiekt zainteresowania na mniejsze objętości (lub elementy), a następnie wielkości fizyczne są rozwiązywane w objętości kontrolnej jako strumienie tych wielkości na różnych ścianach. Stosowane równania są zwykle oparte na zasadzie zachowania lub równowagi wielkości fizycznych, takich jak masa i energia.

Metodę objętości skończonych można zastosować do nieregularnych siatek, podobnie jak metodę elementów skończonych. Równania pierwiastków nadal mają znaczenie fizyczne. Jednak trudno jest uzyskać lepszą dokładność, ponieważ wersje równań pierwiastków wyższego rzędu nie są dobrze zdefiniowane.

Metoda różnic skończonych

Metoda różnic skończonych przybliża równania różniczkowe poprzez aproksymację pochodnej równaniem różniczkowym , co jest główną metodą rozwiązywania równań różniczkowych cząstkowych .

Metoda różnic skończonych

Rozważmy funkcję z jednowartościowymi pochodnymi, które są funkcjami ciągłymi i skończonymi $( x )$ $displaystyle x}$ z twierdzeniem Taylora :

${\ Displaystyle f (x + \ Delta x) = f (x) + \ Delta xf '(x) + {\ Frac {1} {2}} \ Delta x ^ {2} f '' (x) + {\ frac {1}{6}}\Delta x^{3}f'''(x)+\cdots }$

I

${\ Displaystyle f (x- \ Delta x) = f (x) - \ Delta xf '(x) + {\ Frac {1} {2}} \ Delta x ^ {2} f '' (x) - { \frac {1}{6}}\Delta x^{3}f'''(x)+\cdots }$

Podsumowując powyższe wyrażenia:

${\ Displaystyle f (x + \ Delta x) +f(x-\Delta x)=2f(x)+\Delta x^{2}f''(x)+{\text{wyrażenia o wyższej niż czwarta potęga }}\Delta x}$

Zignoruj warunki o wyższej niż czwarta potęga , a następnie: ${\ displaystyle x}$

${\ Displaystyle f '' (x) \ simeq {\ Frac {1} {\Delta x^{2}}}\left[f(x+\Delta x)-2f(x)-f(x-\Delta x)\right]}$

${\ Displaystyle f '(x) \ simeq {\ Frac {1} {2 \ Delta x}} \left[f(x+\Delta x)-f(x-\Delta x)\right]}$

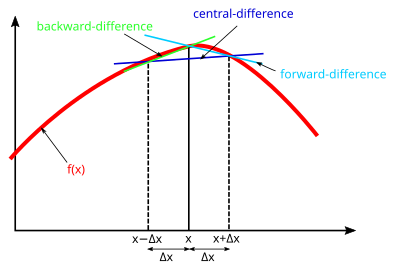
Powyższe jest przybliżeniem pochodnych z różnicą centralną , które można również przybliżyć za pomocą różnicy w przód :

${\ Displaystyle f '(x) \ simeq {\ Frac {1} {\ Delta x}} \ lewo [f ( x+\Delta x)-f(x)\prawo]}$

lub różnica wsteczna :

${\ Displaystyle f '(x) \ simeq {\ Frac {1} {\ Delta x}} \ lewo [f ( x)-f(x-\Delta x)\prawo]}$

Dokładność różnic skończonych można poprawić, stosując terminy wyższego rzędu.

Metoda elementów dyskretnych

Przykład modelu wykorzystującego metodę elementów dyskretnych, który wykorzystuje zdjęcie Petera A. Cundalla do zainicjowania cząstek

Metoda elementów dyskretnych , czasami nazywana metodą elementów odrębnych, jest zwykle stosowana do modelowania materiałów nieciągłych, takich jak skały ze spękaniami, takimi jak spoiny i podłoże, ponieważ umożliwia jawne modelowanie właściwości nieciągłości. Metoda ta została opracowana w celu symulacji mechaniki skał na początku.

Główną ideą tej metody jest modelowanie obiektów jako zbioru mniejszych cząstek, co przypomina budowanie zamku z piasku . Cząstki te mają prostą geometrię, taką jak kula. Wielkości fizyczne każdej cząstki, takie jak prędkość, są stale aktualizowane na stykach między nimi. Ten model jest stosunkowo intensywny obliczeniowo, ponieważ należy użyć dużej liczby cząstek, zwłaszcza w przypadku modeli na dużą skalę, takich jak nachylenie. Dlatego ten model jest zwykle stosowany do obiektów o małej skali.

Model cząstek związanych

Istnieją obiekty, które nie składają się z materiałów ziarnistych, takie jak krystaliczne skały złożone z ziaren mineralnych, które sklejają się ze sobą lub zazębiają. Dodaje się pewne wiązania między cząstkami, aby modelować tę kohezję lub cementację między cząstkami. Ten rodzaj modelu jest również nazywany modelem cząstek związanych.

Aplikacje

Modelowanie numeryczne może być wykorzystywane do modelowania problemów z różnych dziedzin geologii w różnych skalach, takich jak geologia inżynierska , geofizyka , geomechanika , geodynamika , mechanika skał , hydrogeologia i stratygrafia . Poniżej przedstawiono kilka przykładów zastosowań modelowania numerycznego w geologii.

Okaz do skali odkrywki

Mechanika skał

Modelowanie numeryczne znalazło szerokie zastosowanie w różnych dziedzinach mechaniki skał . Skała jest materiałem trudnym do modelowania, ponieważ skały to zazwyczaj:

Nieciągły : w górotworze występują liczne spękania i mikropęknięcia, a przestrzeń w górotworze może być wypełniona innymi substancjami, takimi jak powietrze i woda. Potrzebny jest złożony model, aby w pełni uchwycić te nieciągłości, ponieważ nieciągłości mają ogromny wpływ na górotwór.
Anizotropowy : Właściwości górotworu, takie jak przepuszczalność (zdolność do przepuszczania płynu), mogą zmieniać się w różnych kierunkach.
Niejednorodny : Właściwości różnych części górotworu mogą być różne. Na przykład właściwości fizyczne kwarcu i ziaren skalenia są różne w granicie .
Brak elastyczności : skała nie może idealnie powrócić do swojego pierwotnego kształtu po usunięciu naprężeń.

Do modelowania zachowań skał potrzebny jest złożony model uwzględniający wszystkie powyższe cechy. Istnieje wiele modeli modelujących skałę jako kontinuum przy użyciu metod takich jak metoda różnic skończonych , metoda elementów skończonych i metoda elementów brzegowych . Jedną z wad jest to, że możliwości modelowania pęknięć i innych nieciągłości są zwykle w tych modelach ograniczone. Powszechnie stosowane są również modele, które modelują skałę jako nieciągłość, wykorzystując metody takie jak metody elementów dyskretnych i sieci dyskretnych pęknięć. Opracowano również kombinacje obu metod.

Modelowanie numeryczne poprawia zrozumienie procesów mechanicznych w skale poprzez prowadzenie eksperymentów numerycznych i jest przydatne w pracach projektowych i konstrukcyjnych.

Skala regionalna

termochronologia

Modelowanie numeryczne zostało wykorzystane do przewidywania i opisywania historii termicznej skorupy ziemskiej , co pozwala geologom na lepszą interpretację danych termochronologicznych. Termochronologia może wskazywać czas, w którym skała ostygła poniżej określonej temperatury. Zdarzenia geologiczne, takie jak rozwój uskoków i erozja powierzchni, mogą zmienić termochronologiczny wzór próbek pobranych na powierzchni i możliwe jest ograniczenie zdarzeń geologicznych na podstawie tych danych. Do przewidywania wzorca można zastosować modelowanie numeryczne.

Trudności modelowania termicznego skorupy ziemskiej dotyczą głównie nieregularności i zmian powierzchni Ziemi (głównie erozji ) w czasie. Dlatego w celu modelowania morfologicznych powierzchni Ziemi modele muszą rozwiązywać równania cieplne ze zmieniającymi się w czasie warunkami brzegowymi o nieregularnych oczkach.

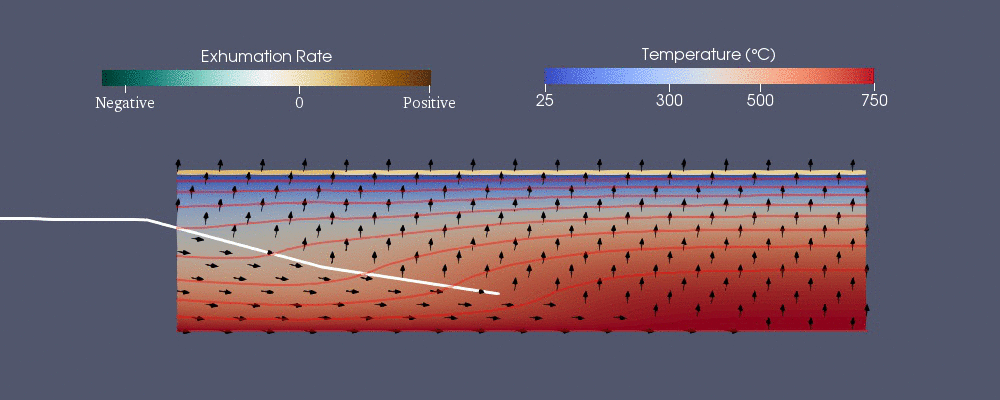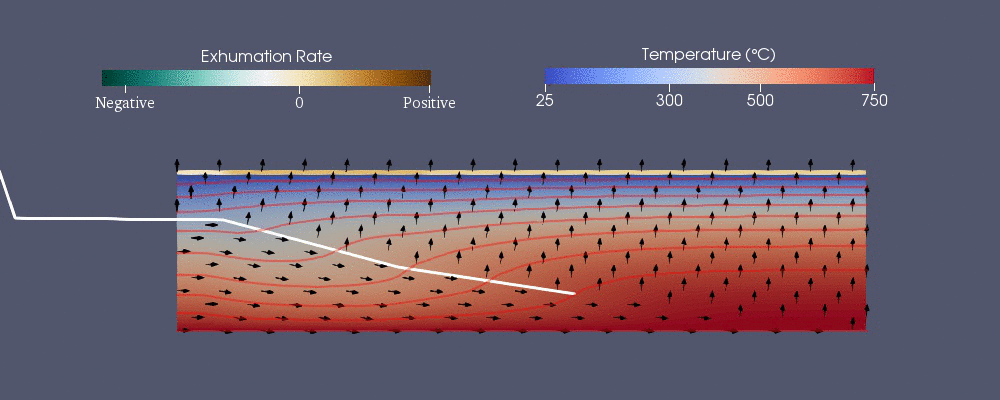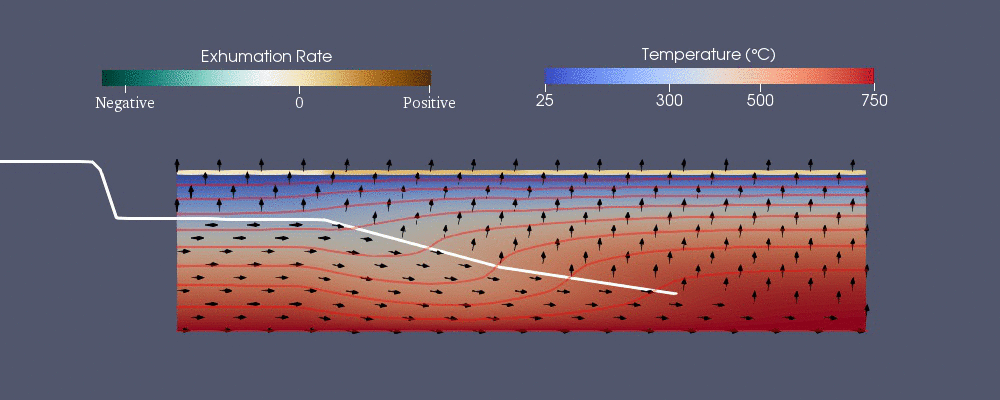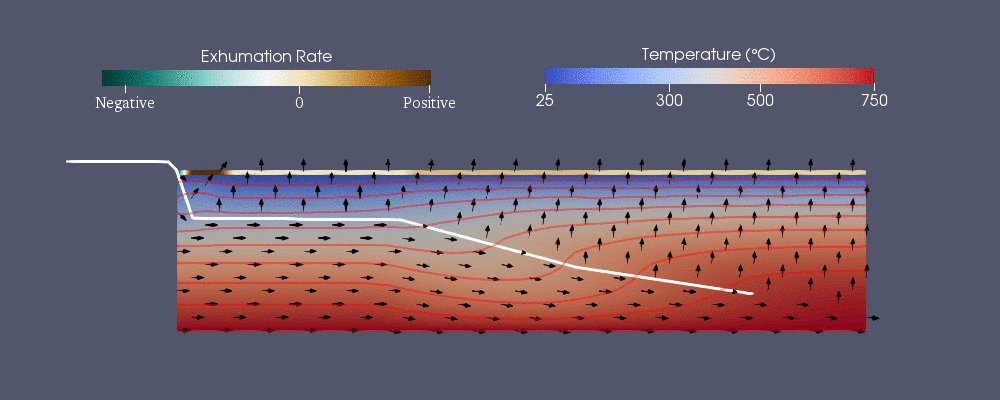
Pecube

Pecube jest jednym z modeli numerycznych opracowanych do przewidywania wzoru termochronologicznego. Rozwiązuje następujące uogólnione równanie wymiany ciepła z adwekcją przy użyciu metody elementów skończonych. Pierwsze $trzy$ $po$ prawej stronie to ciepło przenoszone $przez$ przewodzenie w kierunkach podczas gdy $jest$

{\ Displaystyle {\ Frac {\ częściowy T} {\ częściowy t}} + u {\ Frac {\ częściowy T} {\ częściowy x}} + v {\ Frac {\ częściowy T} {\ częściowy y}} + w {\ frac {\ częściowy T} {\ częściowy z}} = {\ frac {\ częściowy} {\ częściowy x}} \ kappa {\ frac {\ częściowy T} {\ częściowy x}} + {\ frac { \partial }{\częściowy y}}\kappa {\frac {\częściowy T}{\częściowy y}}+{\frac {\częściowy}}{\częściowy z}}\kappa {\frac {\częściowy T}{ \częściowe z}}+A}

Po skonstruowaniu pola temperatury w modelu śledzone są ścieżki cząstek i można uzyskać historię chłodzenia cząstek. Następnie można obliczyć wzór wieku termochronologicznego.

Przekrój pokazujący wzorce termiczne i ekshumacyjne skorupy powstałe w wyniku ruchu uskoku . Symulacja jest generowana przez Pecube [wersja Helsinki University Geodynamics Group (HUGG)]. Model jest trójwymiarowy; rysunek przedstawia wycinek modelu dla uproszczenia. Na rysunku biała linia wskazuje usterkę . Małe czarne strzałki wskazują kierunek ruchu materiału w tym punkcie. Czerwone linie są izotermiczne (punkty linii mają tę samą temperaturę). Model Pecube wykorzystuje zarówno podejście Eulera, jak i Lagrange'a. Uskok można uznać za nieruchomy, a skorupa porusza się. Początkowo temperatura skorupy zależy od głębokości. Im głębsza głębokość, tym cieplejszy materiał. Podczas tego zdarzenia ruch skorupy wzdłuż uskoku przesuwa materiał o różnych temperaturach. W wiszącej ścianie (blok powyżej uskoku) cieplejszy materiał z większej głębokości przesuwa się w kierunku powierzchni; podczas gdy chłodniejszy materiał na płytszej głębokości w spągu (blok poniżej uskoku) przesuwa się głębiej. Przepływ materiału zmienia wzór termiczny (izoterma wygina się w poprzek uskoku) skorupy, co może zresetować termochronometry w skale. Z drugiej strony, ekshumacji wpływa również na termochronometry w skale. Dodatnie tempo ekshumacji wskazuje, że skała porusza się w kierunku powierzchni, podczas gdy ujemne tempo ekshumacji wskazuje, że skała porusza się w dół. Geometria uskoku wpływa na szybkość ekshumacji wzoru na powierzchni.

Hydrogeologia

W hydrogeologii przepływ wód podziemnych jest często modelowany numerycznie metodą elementów skończonych i metodą różnic skończonych. Wykazano, że te dwie metody dają podobne wyniki, jeśli siatka jest wystarczająco drobna.

różnic skończonych używana w MODFLOW

MODFLOW

Jednym ze znanych programów do modelowania przepływu wód podziemnych jest MODFLOW , opracowany przez United States Geological Survey . Jest to darmowy program o otwartym kodzie źródłowym , który wykorzystuje metodę różnic skończonych jako ramy do modelowania warunków wód gruntowych. Niedawny rozwój powiązanych programów oferuje więcej funkcji, w tym:

Oddziaływania między systemami wód podziemnych i powierzchniowych
Transport substancji rozpuszczonych
Przepływ płynu o zmiennej gęstości, takiego jak słona woda
Zagęszczanie systemów wodonośnych
Osiadanie gruntu
Zarządzanie wodami podziemnymi

Dynamika skorupy ziemskiej

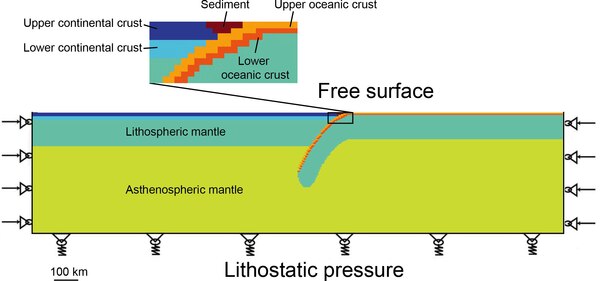
Reologia (reakcja materiałów na naprężenia) skorupy ziemskiej i litosfery jest złożona, ponieważ należy wziąć pod uwagę swobodną powierzchnię (powierzchnię lądu) oraz plastyczność i elastyczność materiałów skorupy ziemskiej. Większość modeli wykorzystuje metody elementów skończonych z siatką Lagrange'a. Jednym z zastosowań jest badanie deformacji i kinematyki subdukcji .

FLAC

Szybka Lagranżowska Analiza Continua (FLAC) jest jednym z najpopularniejszych podejść do modelowania dynamiki skorupy ziemskiej. Podejście to jest szybkie , ponieważ rozwiązuje równania pędu i ciągłości bez użycia macierzy, stąd jest szybkie, ale kroki czasowe muszą być wystarczająco małe. Podejście to było stosowane w badaniach dynamiki skorupy ziemskiej 2D, 2,5D i 3D, w których wyniki 2,5D zostały wygenerowane przez połączenie wielu przekrojów wyników dwuwymiarowych.

Ten rysunek przedstawia konfigurację modelu numerycznego używanego w badaniu ewolucji tektonicznej bloku Cathaysia , który tworzy południowo-wschodnią część kartonu południowochińskiego . Ten model wykorzystuje kod o nazwie Flamar , który jest kodem podobnym do FLAC, który łączy metody różnic skończonych i elementów skończonych. Element użyty w tej siatce Lagrange'a jest czworoboczny. Warunki brzegowe zastosowane do powierzchni terenu są dowolne, na co wpływ ma erozja i depozycja osadów. Granica po bokach ma stałą prędkość, co popchnie skorupę do subdukcji . Warunek brzegowy zastosowany na dole nazywa się „giętką piwnicą Winklera”. Znajduje się w równowadze hydrostatycznej i umożliwia swobodne przesuwanie się podstawy w poziomie.

Skala globalna

Konwekcja płaszcza

Symulacja konwekcji płaszcza w postaci ćwiartki pierścienia 2D za pomocą ASPECT . W modelu temperatura na granicy jądro-płaszcz (wewnętrzna granica) jest stała i wynosi 4273 K (około 4000℃), podczas gdy na granicy między skorupą a płaszczem (granica zewnętrzna) wynosi 973 K (około 700℃). Siatka w symulacji zmienia się w czasie. Kod wykorzystuje adaptacyjne udoskonalanie siatki , siatka jest drobniejsza w obszarach wymagających dokładniejszych obliczeń, takich jak wznoszące się pióropusze, podczas gdy siatka jest grubsza w innych obszarach, aby zaoszczędzić moc obliczeniową. Na rysunku kolor czerwony oznacza wyższą temperaturę, a kolor niebieski wskazuje temperaturę niższą; gorący materiał unosi się z granica rdzenia płaszcza ze względu na mniejszą gęstość. Kiedy gorący materiał dociera do zewnętrznej granicy, zaczyna przemieszczać się poziomo i ostatecznie opada w wyniku ochłodzenia.

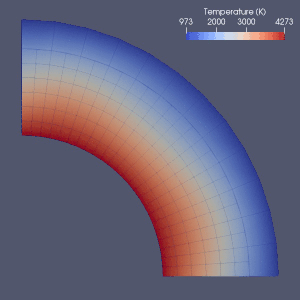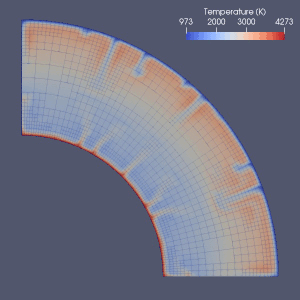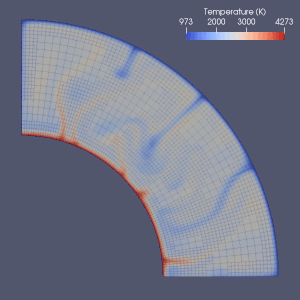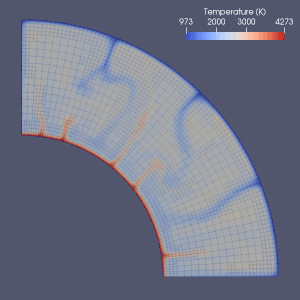
Istnieje wiele prób modelowania konwekcji płaszcza.

Metody elementów skończonych , objętości skończonej , różnic skończonych i metody spektralne zostały wykorzystane do modelowania konwekcji płaszcza, a prawie każdy model wykorzystywał siatkę Eulera. Ze względu na prostotę i szybkość metod różnic skończonych i metod widmowych były one używane w niektórych wczesnych modelach, ale metody elementów skończonych lub metody objętości skończonej zostały ogólnie przyjęte w 2010 roku. Wiele artykułów porównawczych badało ważność tych modeli numerycznych. Obecne podejścia najczęściej wykorzystują stałą i jednolitą siatkę. Udokładnienie siatki, polegające na zmniejszeniu rozmiaru elementów w części wymagającej dokładniejszego przybliżenia, jest prawdopodobnie kierunkiem przyszłego rozwoju numerycznego modelowania konwekcji płaszcza.

Podejście różnic skończonych

W latach sześćdziesiątych do siedemdziesiątych XX wieku modele konwekcji płaszcza wykorzystujące podejście różnic skończonych zwykle wykorzystywały różnice skończone drugiego rzędu . Zastosowano funkcje strumienia , aby usunąć efekt nacisku i zmniejszyć złożoność algorytmu. Ze względu na postęp w technologii komputerowej, skończone różnice z terminami wyższego rzędu są obecnie wykorzystywane do generowania dokładniejszych wyników.

Podejście skończonej objętości

Konwekcja płaszcza modelowana metodą skończonej objętości jest często oparta na równowadze między ciśnieniem a pędem . Wyprowadzone równania są takie same, jak w przypadku metody różnic skończonych, wykorzystującej siatkę z rozłożoną prędkością i ciśnieniem, w której wartości prędkości i ciśnienia każdego elementu znajdują się w różnych punktach. Takie podejście może utrzymać sprzężenie między prędkością a ciśnieniem.

W oparciu o podejście skończonej różnicy/skończonej objętości opracowywanych jest wiele kodów. W modelowaniu trójwymiarowej geometrii Ziemi, ponieważ parametry płaszczy zmieniają się w różnych skalach, w celu przezwyciężenia trudności stosuje się multigrid , czyli stosowanie różnych rozmiarów siatek dla różnych zmiennych. Przykłady obejmują sześcienną siatkę kul, siatkę „Yin-Yang” i siatkę spiralną.

Metoda elementów skończonych

W podejściu elementów skończonych funkcje strumienia są również często używane w celu zmniejszenia złożoności równań. ConMan, modelujący dwuwymiarowy nieściśliwy przepływ w płaszczu, był jednym z popularnych kodów do modelowania konwekcji płaszcza w latach 90. Citcom , model elementów skończonych Eulera typu mutgrid, jest jednym z najpopularniejszych programów do modelowania konwekcji płaszcza w 2D i 3D.

Metoda spektralna

Metoda spektralna w konwekcji płaszcza rozkłada trójwymiarowe równanie rządzące na kilka jednowymiarowych równań, co rozwiązuje równania znacznie szybciej. Było to jedno z popularnych podejść we wczesnych modelach konwekcji płaszcza. Wiele programów zostało opracowanych przy użyciu tej metody w latach 80. do początku XXI wieku. Jednak boczne zmiany lepkości płaszcza są trudne do opanowania w tym podejściu, a inne metody stały się bardziej popularne w 2010 roku.

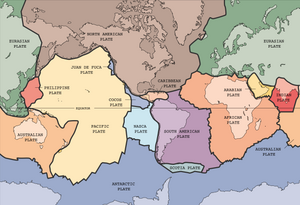
Ziemia składa się z kilku płyt. Do modelowania kinematyki płyt można wykorzystać modele numeryczne.

Płyty tektoniczne

Tektonika płyt to teoria sugerująca, że litosfera ziemska zasadniczo składa się z płyt unoszących się na płaszczu. Model konwekcji płaszcza ma fundamentalne znaczenie w modelowaniu unoszących się na nim płyt i istnieją dwa główne podejścia do włączania płyt do tego modelu: podejście oparte na sztywnych blokach i podejście reologiczne. Podejście ze sztywnymi klockami zakłada, że płyty są sztywne, co oznacza, że zachowują swój kształt i nie odkształcają się, podobnie jak niektóre drewniane klocki unoszące się na wodzie. W przeciwieństwie do tego podejście reologiczne modeluje płyty jako bardzo lepki płyn, w którym równania zastosowane do litosfery poniżej mają również zastosowanie do płyt na górze.

Geodynamika

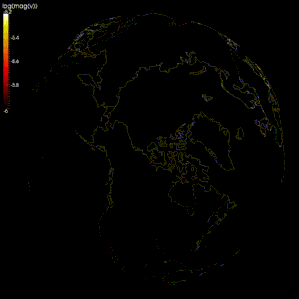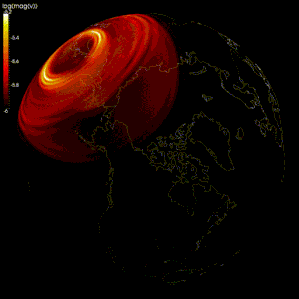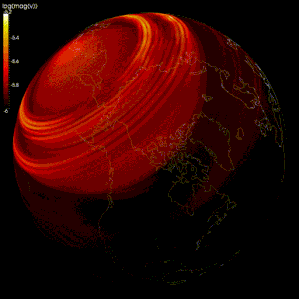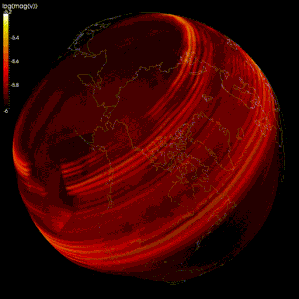
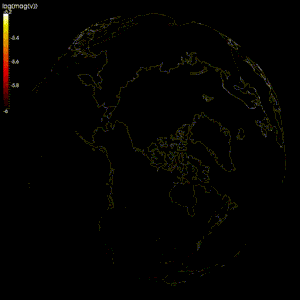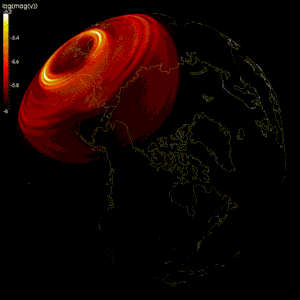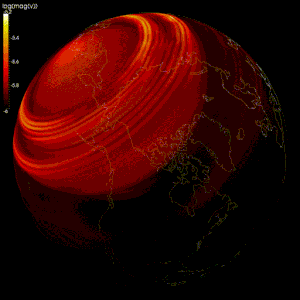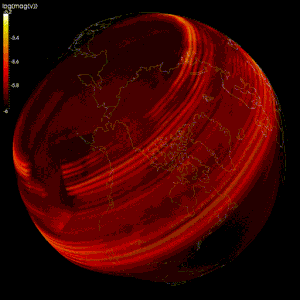
Wykonano modele numeryczne w celu zweryfikowania teorii geodynamo , teorii zakładającej , że pole geomagnetyczne jest generowane przez ruch przewodzącego żelaza i niklu w jądrze Ziemi .

Modelowanie przepływu płynnego jądra zewnętrznego Ziemi jest trudne, ponieważ:

efektu Coriolisa spowodowanego obrotem Ziemi nie można zignorować
pole magnetyczne będzie również generować siłę Lorentza , która wpłynie na ruch płynu przewodzącego w zewnętrznym rdzeniu cieczy
niska lepkość ciekłego żelaza utrudnia modelowanie przepływu płynu

Większość modeli wykorzystuje metodę spektralną do symulacji geodynama, na przykład model Glatzmaiera-Robertsa. Metoda różnic skończonych została również zastosowana w modelu przez Kageyamę i Sato. W niektórych badaniach wypróbowano również inne metody, takie jak metody skończonej objętości i metody elementów skończonych.

Numeryczny model geodynamo (model Glatzmaiera-Robertsa) pokazujący pole magnetyczne generowane przez przepływający płynny rdzeń zewnętrzny. Ten rysunek pokazuje, jak zachowuje się pole magnetyczne Ziemi podczas odwrócenia pola magnetycznego .

Sejsmologia

Symulacja propagacji fali sejsmicznej przez Ziemię.

Metody różnic skończonych są szeroko stosowane w symulacjach propagacji fal sejsmicznych . Jednak ze względu na ograniczenia mocy obliczeniowej, w niektórych modelach rozstaw oczek jest zbyt duży (w porównaniu z długością fal sejsmicznych), przez co wyniki są niedokładne ze względu na dyspersję siatki, w której fale sejsmiczne o różnych częstotliwościach oddzielny. Niektórzy badacze sugerują wykorzystanie metody spektralnej do modelowania propagacji fali sejsmicznej.

Błędy i ograniczenia

Źródła błędów

zawsze istnieje różnica między rzeczywistą obserwacją a wynikami modelowania z powodu:

uproszczenie rzeczywistego problemu przy budowie modelu numerycznego. Ponieważ wiele czynników może wpływać na system geologiczny, uwzględnienie wszystkiego jest prawie niemożliwe. Dlatego model numeryczny zwykle upraszcza rzeczywisty system, pomijając mniej istotne czynniki. Na przykład Ziemia jest często modelowana jako kula, pomimo falowania powierzchni Ziemi.
przybliżenia lub idealizacje rządzących równań. Wiele obiektów w przyrodzie jest złożonych. Niemożliwe jest uchwycenie wszystkich cech za pomocą równań. Na przykład skały są nieciągłe , ale modelowanie skały jako materiału ciągłego jest rozsądne w dużej skali, ponieważ wystarczająco dokładnie opisuje właściwości.
przybliżenia w procesie dyskretyzacji. Ponieważ równań rządzących modelem nie można rozwiązać bezpośrednio, aproksymacji tych równań dokonuje się za pomocą metod dyskretyzacji i numerycznych.
niepewność parametrów fizycznych. Na przykład modele lepkości płaszcza i rdzenia nie są dokładne.

Ograniczenia

Oprócz błędów istnieją pewne ograniczenia w stosowaniu modeli numerycznych:

Użytkownicy modeli potrzebują wysokiego poziomu wiedzy i doświadczenia, aby zapobiec nadużyciom i błędnej interpretacji wyników.

Zobacz też