Nowoczesna geometria trójkąta

Emile Lemoine (1840–1912)

W matematyce nowoczesna geometria trójkąta lub nowa geometria trójkąta to zbiór wiedzy odnoszący się do właściwości trójkąta odkrytego i opracowanego mniej więcej od początku ostatniej ćwierci XIX wieku. Trójkąty i ich właściwości były przedmiotem badań co najmniej od czasów Euklidesa . W rzeczywistości Elementy Euklidesa zawierają opis czterech punktów specjalnych – środka ciężkości , środka , środka okręgu i ortocentrum - związany z trójkątem. Chociaż Pascal i Ceva w XVII wieku, Euler w XVIII wieku i Feuerbach w XIX wieku oraz wielu innych matematyków dokonało ważnych odkryć dotyczących własności trójkąta, dopiero opublikowanie w 1873 roku pracy Emile'a Lemoine'a (1840 –1912) z tytułem „W niezwykłym punkcie trójkąta”, który według Nathana Altschiller-Court został uznany za „położył podwaliny… pod współczesną geometrię trójkąta jako całości”. The American Mathematical Monthly , w którym opublikowano większość prac Lemoine'a, oświadczył, że „Żadnemu z tych [geometrów] bardziej niż Émile-Michel-Hyacinthe Lemoine nie należy się zaszczyt zapoczątkowania tego ruchu współczesnej geometrii trójkątów”. Publikacja tej pracy spowodowała niezwykły wzrost zainteresowania badaniem własności trójkąta w ostatniej ćwierci XIX wieku i na początku XX wieku. Stustronicowy artykuł na temat geometrii trójkątów w Encyklopedii nauk matematycznych Kleina opublikowany w 1914 roku świadczy o tym wzroście zainteresowania geometrią trójkątów.

Na początku wyrażenie „nowa geometria trójkąta” odnosiło się tylko do zestawu interesujących obiektów związanych z trójkątem, takich jak punkt Lemoine'a , koło Lemoine'a, koło Brocarda i linia Lemoine'a . Później rozwinięto teorię korespondencji, która była odgałęzieniem teorii przekształceń geometrycznych, aby nadać spójność różnym pojedynczym wynikom. Wraz z rozwojem wyrażenie „nowa geometria trójkąta” wskazywało nie tylko na wiele niezwykłych obiektów związanych z trójkątem, ale także na metody stosowane do badania i klasyfikacji tych obiektów. Oto definicja geometrii trójkąta z 1887 roku: „Mając dany punkt M na płaszczyźnie trójkąta, możemy zawsze znaleźć na nieskończoną liczbę sposobów drugi punkt M', który odpowiada pierwszemu zgodnie z wyimaginowanym geometrycznym prawo; te dwa punkty mają między sobą relacje geometryczne, których prostota zależy od mniej więcej szczęśliwego wyboru prawa, które je łączy, a każde prawo geometryczne daje początek metodzie transformacji, trybowi koniugacji, który pozostaje do zbadania. (Patrz artykuł konferencyjny zatytułowany „Nauczanie nowych metod geometrycznych za pomocą starożytnej figury w XIX i XX wieku: nowa geometria trójkąta w podręcznikach w Europie i USA (1888–1952)” autorstwa Pauline Romera-Lebret przedstawiony w 2009 r.)

Jednak ta eskalacja zainteresowania szybko się załamała, a geometria trójkąta była całkowicie zaniedbywana aż do ostatnich lat XX wieku. W swoim „Development of Mathematics” Eric Temple Bell przedstawia swoją ocenę statusu współczesnej geometrii trójkątów w 1940 roku w ten sposób: „Geometrzy XX wieku już dawno pobożnie przenieśli wszystkie te skarby do muzeum geometrii, gdzie pył historii szybko przyćmiły ich blask”. (The Development of Mathematics, s. 323) Philip Davis zasugerował kilka przyczyn spadku zainteresowania geometrią trójkąta. Obejmują one:

Poczucie, że przedmiot jest elementarny i ma niski status zawodowy.
Wyczerpanie jej możliwości metodologicznych.
Wizualna złożoność tak zwanych głębszych wyników przedmiotu.
Degradacja wizualnego na rzecz algebraicznego.
Brak powiązań z innymi dziedzinami.
Rywalizacja z innymi tematami o silnej treści wizualnej, takimi jak teselacje , fraktale , teoria grafów itp.

Dalsze ożywienie zainteresowania nastąpiło wraz z pojawieniem się nowoczesnego komputera elektronicznego . Geometria trójkąta ponownie stała się aktywnym obszarem badań prowadzonych przez grupę oddanych geometrów. Jako uosobienie tego odrodzenia można wskazać sformułowanie koncepcji „ środka trójkąta ” i opracowanie przez Clarka Kimberlinga encyklopedii środków trójkątów zawierającej listę prawie 50 000 środków trójkątów i ich właściwości, a także zestawienie katalogu z trójkątów sześciennych ze szczegółowymi opisami kilku właściwości ponad 1200 trójkątów sześciennych. Otwarty dostęp do czasopisma Forum Geometricorum, założonego przez Paula Yiu z Florida Atlantic University w 2001 r., również dostarczył ogromnego impulsu do rozwijania tego nowo odkrytego entuzjazmu dla geometrii trójkątów. Niestety, od 2019 r. czasopismo nie przyjmuje zgłoszeń, chociaż starsze numery są nadal dostępne online.

Geometria Lemoine'a

Punkt Lemoine'a

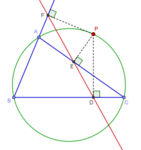
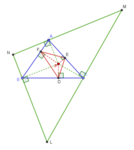
Dla danego trójkąta ABC o środku ciężkości G, symmediana przechodząca przez wierzchołek jest odbiciem prostej AG w dwusiecznej kąta A. Istnieją trzy symmediany trójkąta przechodzącego przez każdy wierzchołek. Trzy symmediany są współbieżne, a punkt zbieżności, zwykle oznaczany przez K, nazywany jest punktem Lemoine'a lub punktem symmediany lub punktem Grebe'a trójkąta ABC. Jeśli długości boków trójkąta ABC wynoszą a , b , c , współrzędne barycentryczne punktu Lemoine'a wynoszą a ² : b ² : do ² . Został on opisany jako „jeden z klejnotów koronnych współczesnej geometrii”. Istnieje kilka wcześniejszych odniesień do tego punktu w literaturze matematycznej, których szczegóły są dostępne w historii punktu symmediany Johna Mackaya.

W rzeczywistości zbieżność symmedian jest szczególnym przypadkiem bardziej ogólnego wyniku: dla dowolnego punktu P na płaszczyźnie trójkąta ABC, izogony prostych AP, BP, CP są zbieżne, izogonalna AP (odpowiednio BP, CP) będące odbiciem prostej AP w dwusiecznej kąta A (odpowiednio B, C). Punkt współbieżności nazywany jest izogonalnym koniugatem P. W tej terminologii punkt Lemoine'a jest izogonalnym sprzężeniem środka ciężkości.

Kręgi Lemoine'a

Punkty przecięcia prostych przechodzących przez punkt Lemoine'a trójkąta ABC równoległych do boków trójkąta leżą na okręgu zwanym pierwszym okręgiem Lemoine'a trójkąta ABC. Środek pierwszego koła Lemoine'a leży w połowie odległości między środkiem okręgu opisanego a punktem Lemoine'a trójkąta,

Punkty przecięcia antyrównoległości do boków trójkąta ABC przez punkt Lemoine'a trójkąta ABC leżą na okręgu zwanym drugim kołem Lemoine'a lub kosinusem trójkąta ABC. Nazwa "koło cosinusowe" wynika z właściwości drugiego koła Lemoine'a, że długości odcinków przecinanych przez koło po bokach trójkąta są proporcjonalne do cosinusów kątów przeciwległych do boków. Środek drugiego okręgu Lemoine'a to punkt Lemoine'a.

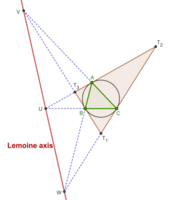
oś Lemoine'a

Dowolny trójkąt ABC i jego trójkąt styczny są w perspektywie , a oś perspektywy nazywana jest osią Lemoine'a trójkąta ABC. Jest to biegun trójliniowy punktu symediany trójkąta ABC, a także biegun K w odniesieniu do okręgu opisanego na trójkącie ABC.

Trójkąt z medianami (czarny), dwusiecznymi kątów (kropkowane) i symmedianami (czerwony). Symmediany przecinają się w punkcie symediany (oznaczonym na rysunku przez L), dwusieczne kątów w środku I i środkowe w środku ciężkości G.
Pierwszy okrąg Lemoine'a trójkąta ABC. Pokazano również punkt Lemoine K, środek I, środek ciężkości G i linie przechodzące przez K równoległe do boków.
Drugie koło Lemoine'a trójkąta ABC. Pokazano również punkt Lemoine K, środek I, środek ciężkości G i linie przechodzące przez K przeciwrównoległe do boków.
Oś Lemoine'a trójkąta ABC. Pokazano również trójkąt styczny.

Wczesna nowożytna geometria trójkąta

Poniżej przedstawiono szybki rzut oka na świat współczesnej geometrii trójkątów, jaki istniał w szczytowym okresie zainteresowania geometrią trójkątów po opublikowaniu artykułu Lemoine'a. Ta prezentacja jest w dużej mierze oparta na tematach omówionych w książce Williama Gallatly'ego opublikowanej w 1910 roku i książce Rogera A. Johnsonsa opublikowanej po raz pierwszy w 1929 roku.

Porystyczne trójkąty

Mówi się, że dwa trójkąty są trójkątami porowymi, jeśli mają ten sam okrąg i okrąg opisany. Mając okrąg o środku O i promieniu R oraz inny okrąg o środku I i promieniu r , istnieje nieskończona liczba trójkątów ABC z okręgiem O( R ) jako okręgiem opisanym i I ( r ) jak okręgiem wtedy i tylko wtedy, gdy {{{ 1}}} . Trójkąty te tworzą porystyczny układ trójkątów. Loci pewnych specjalnych punktów, takich jak środek ciężkości, ponieważ trójkąt odniesienia śledzi różne trójkąty porystyczne, okazuje się, że są to okręgi i punkty.

Linia Simsona

Dla dowolnego punktu P na okręgu opisanym na trójkącie ABC, stopy prostopadłych od P do boków trójkąta ABC są współliniowe, a prostą współliniowości jest dobrze znana prosta Simsona z P.

Trójkąt pedałowy i antypedałowy

Mając dany punkt P, niech ramiona prostopadłych z P do boków trójkąta ABC będą D, E, F. Trójkąt DEF nazywamy trójkątem pedałowym P. Trójkąt przeciwnożny P jest trójkątem utworzonym przez proste przechodzące przez A, B, C prostopadłe odpowiednio do PA, PB, PC. Dwa punkty P i Q nazywane są punktami przeciwnymi , jeśli trójkąt pedałowy P jest homotetyczny względem trójkąta przeciwnożnego Q, a trójkąt pedałowy Q jest homotetyczny względem trójkąta przeciwnożnego P.

ortobieg

Mając dowolną prostą l , niech P, Q, R będą stopami prostopadłych z wierzchołków A, B, C trójkąta ABC do l . Proste przechodzące przez P. Q, R prostopadłe odpowiednio do boków BC, CA, AB są zbieżne, a punktem przecięcia jest ortopol prostej l względem trójkąta ABC. We współczesnej geometrii trójkąta istnieje obszerna literatura dotycząca właściwości ortopoli.

Punkty Brocarda

Oznaczmy okręgi bokami BC, CA, AB trójkąta ABC, którego zewnętrzne odcinki zawierają odpowiednio dwie triady kątów C, A, B i B, C, A. Każda triada okręgów określona przez triadę kątów przecina się we wspólnym punkcie, dając w ten sposób dwa takie punkty. Punkty te nazywane są punktami Brocarda trójkąta ABC i są zwykle oznaczane przez ${\ Displaystyle \ Omega, \ Omega ^ {\ pierwsza}}$ . Jeśli P jest pierwszym punktem Brocarda (który jest punktem Brocarda określonym przez pierwszą triadę okręgów), to kąty PBC, PCA i PAB są sobie równe, a wspólny kąt nazywany jest kątem Brocarda trójkąta ABC i jest powszechnie oznaczany przez ${\ displaystyle \ omega}$ Kąt Brocarda jest określony przez

{\ Displaystyle \ łóżeczko \ omega = \ łóżeczko A + \ łóżeczko B + \ łóżeczko C.}

Punkty Brocarda i kąty Brocarda mają kilka interesujących właściwości.

Niektóre obrazy

Dwa porystyczne trójkąty ABC i A'B'C' względem okręgów I( r ) i O( R )
Linia Simsona P
Trójkąt pedałowy (DEF) i trójkąt przeciwpedałowy (LMN) P
Ortobieg linii l
Pierwszy punkt Brocarda trójkąta ABC

Współczesna nowoczesna geometria trójkąta

Centrum trójkąta

Jedną z najbardziej znaczących idei, która pojawiła się podczas odrodzenia zainteresowania geometrią trójkąta w ostatnich latach XX wieku, jest pojęcie środka trójkąta . Ta koncepcja, wprowadzona przez Clarka Kimberlinga w 1994 roku, zjednoczyła w jednym pojęciu bardzo wiele specjalnych i niezwykłych punktów związanych z trójkątem. Od czasu wprowadzenia tego pomysłu prawie żadna dyskusja na temat jakiegokolwiek wyniku związanego z trójkątem nie jest kompletna bez dyskusji na temat tego, w jaki sposób wynik łączy się ze środkami trójkąta.

Definicja środka trójkąta

Funkcja f o wartościach rzeczywistych trzech zmiennych rzeczywistych a , b , c może mieć następujące własności:

Jednorodność: f ( ta , tb , tc ) = t ⁿ f ( a , b , c ) dla pewnej stałej n i dla wszystkich t > 0.
Bisymetria w drugiej i trzeciej zmiennej: f ( a , b , c ) = f ( a , c , b ).

Jeśli niezerowa f ma obie te właściwości, nazywana jest funkcją środka trójkąta . Jeśli f jest środkiem trójkąta, a a , b , c są długościami boków trójkąta odniesienia, to punkt, którego trójliniowe współrzędne to f ( a , b , c ): f ( b , c , a ): f ( c , _ _ b ) nazywamy środkiem trójkąta .

Clark Kimberling prowadzi stronę internetową poświęconą kompendium środków trójkątów. Witryna o nazwie Encyklopedia centrów trójkątów zawiera definicje i opisy prawie 50 000 centrów trójkątów.

Centralna linia

Innym jednoczącym pojęciem współczesnej nowoczesnej geometrii trójkąta jest linia środkowa . Ta koncepcja łączy kilka specjalnych linii prostych związanych z trójkątem. Pojęcie linii środkowej jest również związane z pojęciem środka trójkąta.

Definicja linii centralnej

Niech ABC będzie trójkątem płaskim i niech ( x : y : z ) będzie trójliniowymi współrzędnymi dowolnego punktu na płaszczyźnie trójkąta ABC .

Prosta w płaszczyźnie trójkąta ABC , którego równanie we współrzędnych trójliniowych ma postać

fa ( za , b , do ) x + sol ( za , b , do ) y + godz ( za , b , do ) z = 0

gdzie punkt o współrzędnych trójliniowych ( f ( a , b , c ) : g ( a , b , c ) : h ( a , b , c ) ) jest środkiem trójkąta, jest linią środkową płaszczyzny trójkąta ABC względną do trójkąta ABC .

Geometryczna konstrukcja linii centralnej

Niech X będzie dowolnym środkiem trójkąta ABC .

Narysuj linie AX , BX i CX oraz ich odbicia w dwusiecznych wewnętrznych kątów odpowiednio w wierzchołkach A , B , C .
Odbite linie są zbieżne, a punktem zbieżności jest izogonalny sprzężony Y z X .
Niech ceviany AY , BY , CY spotkają się z przeciwległymi liniami bocznymi trójkąta ABC odpowiednio w punktach A' , B' , C' . Trójkąt A'B'C ' jest trójkątem cewiuszowym Y. _ _
Trójkąt ABC i trójkąt cewiański A ' B ' C ' są w perspektywie i niech DEF będzie osią perspektywy tych dwóch trójkątów. Linia DEF jest trójliniową biegunową punktu Y . Linia DEF jest linią środkową powiązaną ze środkiem trójkąta X .

Stożki trójkątne

Stożek trójkąta jest stożkiem w płaszczyźnie trójkąta odniesienia i jest z nim w jakiś sposób powiązany. Na przykład okrąg opisany i wpisany w trójkąt odniesienia to trójkąty stożkowe. Inne przykłady to elipsa Steinera , która jest elipsą przechodzącą przez wierzchołki i mającą środek w środku ciężkości trójkąta odniesienia, hiperbola Kieperta , która jest stożkiem przechodzącym przez wierzchołki, środek ciężkości i ortocentrum trójkąta odniesienia i paraboli Artzta, które są parabolami stykającymi się z dwiema liniami bocznymi trójkąta odniesienia w wierzchołkach trójkąta. Niektóre ostatnio badane stożki trójkątne obejmują elipsy Hofstadtera i stożki yff . Jednak nie ma formalnej definicji terminologii trójkąta stożkowego w literaturze; to znaczy relacje, jakie powinien mieć stożek z trójkątem odniesienia, aby kwalifikować go do miana trójkąta stożkowego, nie zostały precyzyjnie sformułowane. WolframMathWorld ma stronę zatytułowaną „Triangle conics”, która zawiera listę 42 pozycji (nie wszystkie z nich to stożki) bez podania definicji trójkąta stożkowego.

Elipsa Steinera
Parabole Artza
Hiperbola Kieperta

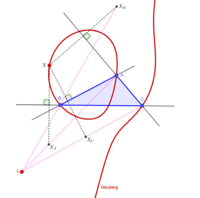
Sześcienne trójkąty

Krzywe sześcienne pojawiają się naturalnie w badaniu trójkątów. Na przykład miejsce punktu P na płaszczyźnie trójkąta odniesienia ABC takie, że jeśli odbicia P na bokach trójkąta ABC to P a , P b , P _c , _to proste _AP a _, BP _b i CP _c są współbieżne to krzywa sześcienna o nazwie sześcienny Neuberg . Jest to pierwszy sześcienny wymieniony w Katalogu sześciennych trójkątów Bernarda Gilberta . Ten katalog zawiera ponad 1200 trójkątów sześciennych z informacjami na temat każdej krzywej, takimi jak równanie barycentryczne krzywej, środki trójkątów leżące na krzywej, właściwości locus krzywej i odniesienia do literatury na temat krzywej.

Sześcienny Neuberga ( K001 )
Sześcienny McCay z trzema równoległymi asymptotami ( K003 )
Tucker sześcienny ( K011 )

Komputery w geometrii trójkąta

Pojawienie się komputerów miało decydujący wpływ na przebieg rozwoju zainteresowania geometrią trójkątów, obserwowany w ostatnich latach XX wieku i na początku obecnego stulecia. Niektóre sposoby, w jakie komputery wpłynęły na ten kurs, zostały nakreślone przez Philipa Davisa. Komputery zostały wykorzystane do wygenerowania nowych wyników w geometrii trójkąta. Artykuł z ankiety opublikowany w 2015 roku zawiera opis niektórych ważnych nowych wyników odkrytych przez program komputerowy „Dircoverer”. Poniższa próbka twierdzeń daje przedsmak nowych wyników odkrytych przez Discoverer.

Twierdzenie 6.1 Niech P i Q będą punktami, z których żaden nie leży na boku trójkąta ABC. Jeśli P i Q są koniugatami izogonalnymi względem ABC, to iloczyn Ceva ich dopełnień leży na hiperboli Kieperta.
Twierdzenie 9.1. Środek kongruencji Yff jest wewnętrznym środkiem podobieństwa okręgu wpisanego i okręgu opisanego w odniesieniu do trójkąta pedałowego środka.
Koło Lestera to okrąg, który przechodzi przez środek okręgu opisanego, środek dziewięciopunktowy oraz zewnętrzne i wewnętrzne punkty Fermata. Uogólniony okrąg Lestera to okrąg, który przechodzi przez co najmniej cztery środki trójkąta. Odkrywca odkrył kilka uogólnionych kręgów Lestera.

Sava Grozdev, Hiroshi Okumura, Deko Dekov prowadzą portal internetowy poświęcony odkrytej komputerowo encyklopedii geometrii euklidesowej.

Dodatkowa lektura

Johna Mackaya (1896). „Symmedianie trójkąta i ich kręgi towarzyszące” (PDF) . Postępowanie z matematyki w Edynburgu . soc . XIV : 37–103 . Źródło 7 stycznia 2022 r .
Williama Gallatly'ego (1910). Współczesna geometria trójkąta . Londyn: Francis Hodgson . Źródło 4 stycznia 2022 r .
Rossa Honsbergera (1995). Epizody w dziewiętnastowiecznej i dwudziestowiecznej geometrii euklidesowej . Amerykańskie Stowarzyszenie Matematyczne.
Roger Johnson (31 sierpnia 2007). Zaawansowana geometria euklidesowa . Dover Publications Inc. ISBN 978-0486462370 .
HSM Coexter (5 września 1996). Geometria po raz kolejny . Amerykańskie Stowarzyszenie Matematyczne. ISBN 0883856190 .
Altshiller-Court, Nathan (1952). geometria uczelni; wprowadzenie do współczesnej geometrii trójkąta i koła . Nowy Jork: Barnes & Noble . Źródło 10 stycznia 2022 r .
Kimberling, C (1998). „Centra trójkątów i trójkąty środkowe”. Kongr. liczba. : 1–295.
Paul Yiu (grudzień 2012). Wprowadzenie do geometrii trójkąta (PDF) . Wydział Matematyki Florida Atlantic University . Źródło 5 stycznia 2022 r .
Scott, Charlotte Angas (1894). Wstępne omówienie niektórych współczesnych idei i metod płaskiej geometrii analitycznej . Londyn: Macmillan and Co. Źródło 10 stycznia 2022 r .