Ruch uliczny

W matematyce i inżynierii transportu przepływ ruchu to badanie interakcji między podróżnymi (w tym pieszymi, rowerzystami, kierowcami i ich pojazdami) a infrastrukturą (w tym autostradami, oznakowaniem i urządzeniami kontroli ruchu) w celu zrozumienia i opracowania optymalnego sieci transportowej o sprawnym ruchu i minimalnych problemach z zatłoczeniem .

Historia

Próby stworzenia matematycznej teorii przepływu ruchu sięgają lat dwudziestych XX wieku, kiedy Frank Knight po raz pierwszy przedstawił analizę równowagi ruchu, którą w 1952 roku doprecyzowano w pierwszą i drugą zasadę równowagi Wardropa .

Niemniej jednak, nawet wraz z pojawieniem się znacznej mocy obliczeniowej komputerów, do tej pory nie było zadowalającej ogólnej teorii, którą można by konsekwentnie zastosować do rzeczywistych warunków przepływu. Obecne modele ruchu wykorzystują mieszankę technik empirycznych i teoretycznych . Modele te są następnie opracowywane w prognozach ruchu i uwzględniają proponowane lokalne lub poważne zmiany, takie jak zwiększone wykorzystanie pojazdów, zmiany w użytkowaniu gruntów lub zmiany w środkach transportu (na przykład ludzie przesiadają się z autobusu do pociągu lub samochodu), oraz zidentyfikować obszary zatory , w przypadku których sieć wymaga dostosowania.

Przegląd

Pojemność pasażerska różnych środków transportu

Wymagania dotyczące przestrzeni drogowej

Ruch drogowy zachowuje się w sposób złożony i nieliniowy, w zależności od interakcji dużej liczby pojazdów . Ze względu na indywidualne reakcje ludzkich kierowców, pojazdy nie wchodzą w interakcje ^{gęstości pojazdu , po} prostu zgodnie z prawami mechaniki, ale raczej tworzą skupiska i propagację fali uderzeniowej , zarówno do przodu jak i do tyłu, w zależności od . Niektóre modele matematyczne przepływu ruchu wykorzystują kolejkę pionową założenie, że pojazdy na zatłoczonym odcinku nie cofają się wzdłuż odcinka.

W sieci o swobodnym przepływie teoria przepływu ruchu odnosi się do zmiennych strumienia ruchu, takich jak prędkość, przepływ i koncentracja. Zależności te dotyczą głównie niezakłóconego przepływu ruchu, występującego przede wszystkim na autostradach lub drogach ekspresowych. Warunki przepływu są uważane za „swobodne”, gdy na drodze znajduje się mniej niż 12 pojazdów na milę na pas ruchu. „Stabilny” jest czasami określany jako 12–30 pojazdów na milę na pas. Gdy gęstość osiągnie maksymalne masowe natężenie przepływu (lub strumień ) i przekroczy optymalną gęstość (powyżej 30 pojazdów na milę na pas), przepływ ruchu staje się niestabilny, a nawet drobny incydent może spowodować trwałe warunki jazdy typu stop-and-go . Stan „awarii” występuje, gdy ruch staje się niestabilny i przekracza 67 pojazdów na milę na pasie. „Gęstość korków” odnosi się do ekstremalnego natężenia ruchu, gdy natężenie ruchu całkowicie się zatrzymuje, zwykle w zakresie 185–250 pojazdów na milę na pas.

Obliczenia dotyczące przeciążonych sieci są jednak bardziej złożone i opierają się bardziej na badaniach empirycznych i ekstrapolacjach z rzeczywistych liczb dróg. Ponieważ często mają one charakter miejski lub podmiejski, inne czynniki (takie jak bezpieczeństwo użytkowników dróg i względy środowiskowe) również wpływają na optymalne warunki.

Właściwości strumienia ruchu

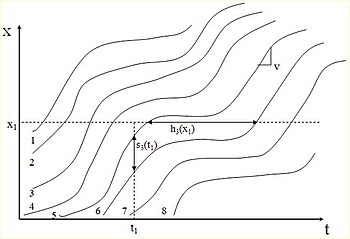
Przepływ ruchu jest na ogół ograniczony wzdłuż jednowymiarowej ścieżki (np. pasa ruchu). Diagram czasoprzestrzenny przedstawia graficznie przepływ pojazdów wzdłuż ścieżki w czasie. Czas jest wyświetlany na osi poziomej, a odległość na osi pionowej. Ruch drogowy na diagramie czasoprzestrzennym jest reprezentowany przez poszczególne linie trajektorii poszczególnych pojazdów. Pojazdy jadące po sobie wzdłuż danego pasa ruchu będą miały trajektorie równoległe, a trajektorie będą się krzyżować, gdy jeden pojazd mija drugi. Diagramy czasoprzestrzenne są przydatnymi narzędziami do wyświetlania i analizowania charakterystyk przepływu ruchu na danym odcinku jezdni w czasie (np. analiza natężenia ruchu).

Istnieją trzy główne zmienne do wizualizacji strumienia ruchu: prędkość (v), gęstość (oznaczona k; liczba pojazdów na jednostkę przestrzeni) i przepływ [ ^{wymagane wyjaśnienie ]} (oznaczona q; liczba pojazdów na jednostkę czasu) .

Rysunek 1. Diagram czasoprzestrzeni

Prędkość

Prędkość to odległość pokonywana w jednostce czasu. Nie można śledzić prędkości każdego pojazdu; tak więc w praktyce średnia prędkość jest mierzona poprzez pobieranie próbek pojazdów na danym obszarze w określonym czasie. Zidentyfikowano dwie definicje średniej prędkości: „średnia prędkość w czasie” i „średnia prędkość w przestrzeni”.

„Średnia prędkość w czasie” jest mierzona w punkcie odniesienia na jezdni w pewnym okresie czasu. W praktyce mierzy się to za pomocą detektorów pętli. Detektory pętli rozmieszczone na obszarze odniesienia mogą zidentyfikować każdy pojazd i śledzić jego prędkość. Jednak pomiary średniej prędkości uzyskane tą metodą nie są dokładne, ponieważ prędkości chwilowe uśrednione dla kilku pojazdów nie uwzględniają różnicy w czasie podróży dla pojazdów poruszających się z różnymi prędkościami na tej samej odległości. ^{[ wymagane wyjaśnienie ]}
${\ Displaystyle v_ {t} = (1/m) \ suma _ {i = 1} ^ {m} v_ {i}}$

gdzie m oznacza liczbę pojazdów przejeżdżających przez stały punkt, a v _i to prędkość i- tego pojazdu.
„Średnia prędkość w przestrzeni” jest mierzona na całym odcinku jezdni. Kolejne zdjęcia lub wideo segmentu jezdni śledzą prędkość poszczególnych pojazdów, a następnie obliczana jest średnia prędkość. Uważa się, że jest dokładniejszy niż średnia prędkość w czasie. Dane do obliczania średniej prędkości w przestrzeni mogą pochodzić ze zdjęć satelitarnych, aparatu fotograficznego lub obu. ${\ Displaystyle v_ {s} = \ lewo ((1/n) \ suma _ {i = 1} ^ {n} (1 / v_ {i}) \ prawo) ^ {- 1}}$
gdzie n oznacza liczbę pojazdów przejeżdżających przez odcinek jezdni.

„Średnia prędkość w przestrzeni” jest zatem średnią harmoniczną prędkości. Średnia prędkość w czasie nigdy nie jest mniejsza niż średnia prędkość w przestrzeni: ${\ Displaystyle v_ {t} = v_ {s} + {\ Frac {\ sigma _ {s} ^ {2} σ s 2 {\ Displaystyle \ sigma _ {s} ^ {2}} jest wariancją średniej prędkości w przestrzeni σ s 2 {\ Displaystyle \ sigma _$ $}$ ^ {2}

Rysunek 2. Średnie prędkości przestrzenne i średnie czasowe

Na diagramie czasoprzestrzennym prędkość chwilowa pojazdu v = dx/dt jest równa nachyleniu wzdłuż trajektorii pojazdu. Średnia prędkość pojazdu jest równa nachyleniu linii łączącej punkty końcowe trajektorii, w których pojazd wjeżdża i wyjeżdża z odcinka jezdni. Pionowa separacja (odległość) między równoległymi trajektoriami to odległość (s) pojazdów między pojazdem poprzedzającym i jadącym z tyłu. Podobnie separacja pozioma (czas) reprezentuje drogę pojazdu (h). Diagram czasoprzestrzenny jest przydatny do powiązania odpowiednio drogi i odstępów z natężeniem ruchu i gęstością.

Gęstość

Gęstość (k) definiowana jest jako liczba pojazdów na jednostkę długości jezdni. W przepływie ruchu dwie najważniejsze gęstości to gęstość krytyczna ( _kc ) i gęstość korków ( kj ) _. Maksymalna gęstość osiągalna przy swobodnym przepływie wynosi kc _, podczas gdy kj jest maksymalną gęstością osiąganą przy przeciążeniu _. Ogólnie gęstość zacięcia jest pięciokrotnie większa od gęstości krytycznej. Odwrotnością gęstości jest odstęp (s), czyli odległość od środka do środka między dwoma pojazdami.

${\ Displaystyle k = {\ Frac {1} {s}}}$

Rysunek 3. Zależność Gęstość przepływu

Rysunek 4. Zależność między przepływem ( q ), gęstością ( k ) i prędkością ( v )

Gęstość ( k ) na długości jezdni ( L ) w danym czasie ( t ₁ ) jest równa odwrotności średniego odstępu n pojazdów .

${\ Displaystyle K (L, t_ {1}) = {\ Frac {n} {L}} = {\ Frac {1} {{{ \bar {s}}(t_{1})}}}$

Na diagramie czasoprzestrzennym gęstość można oszacować w obszarze A.

${\ Displaystyle k (A) = {\ Frac {n} {L}} = {\ Frac {n \, dt} {L \, dt}} = {\ Frac {tt} {\ lewo | A \ prawo \ odwróć }}}$

gdzie tt to całkowity czas podróży w A .

Rysunek 5

Przepływ

Przepływ ( q ) to liczba pojazdów przejeżdżających przez punkt odniesienia w jednostce czasu, pojazdach na godzinę. Odwrotność przepływu to posuw ( h ), czyli czas, jaki upływa między i- tym pojazdem mijającym punkt odniesienia w przestrzeni a ( i + 1)-tym pojazdem. W zatłoczeniu h pozostaje stałe. Gdy tworzy się korek uliczny, h zbliża się do nieskończoności.

${\ displaystyle q = kv \,}$

${\ Displaystyle q = 1 / h \,}$

Przepływ ( q ) przepływający przez stały punkt ( x ₁ ) w przedziale ( T ) jest równy odwrotności średniego postępu m pojazdów.

${\ Displaystyle q (T, x_ {1}) = {\ Frac {m} {T}} = {\ Frac {1} {{{ \bar {h}}(x_{1})}}}$

Na diagramie czasoprzestrzennym przepływ można ocenić w obszarze B .

${\ Displaystyle q (B) = {\ Frac {m} {T}} = {\ Frac {m \, dx} T \, dx}} = {\ Frac {td} {\ lewo | B \ prawo \ odwróć }}}$

gdzie td jest całkowitą drogą przebytą w B .

Rysunek 6

Metody analizy

Analitycy podchodzą do problemu na trzy główne sposoby, odpowiadające trzem głównym skalom obserwacji w fizyce:

Skala mikroskopowa : Na najbardziej podstawowym poziomie każdy pojazd jest traktowany jako jednostka. Dla każdego można napisać równanie, zwykle równanie różniczkowe zwyczajne (ODE). Można również zastosować modele automatyzacji komórkowej, w których droga jest podzielona na komórki, z których każda zawiera poruszający się samochód lub jest pusta. Prostym przykładem takiego modelu jest model Nagela -Schreckenberga . Gdy samochody wchodzą w interakcje, może modelować zjawiska zbiorowe, takie jak korki uliczne .
Skala makroskopowa : Podobnie jak w przypadku modeli dynamiki płynów , za przydatne uważa się zastosowanie układu równań różniczkowych cząstkowych , które równoważą prawa dla pewnych wielkości brutto będących przedmiotem zainteresowania; np. gęstość pojazdów lub ich średnia prędkość.
Skala mezoskopowa (kinetyczna): Trzecią, pośrednią możliwością jest zdefiniowanie funkcji, która wyraża prawdopodobieństwo posiadania pojazdu w czasie $t$ $}$ w pozycji $która$ $działa$ z . Funkcję tę, zgodnie z metodami mechaniki statystycznej , można obliczyć za pomocą równania całkowo-różnicowego, takiego jak równanie Boltzmanna .

Inżynierskie podejście do analizy problemów przepływu ruchu na autostradzie opiera się przede wszystkim na analizie empirycznej (tj. obserwacji i matematycznym dopasowaniu krzywej). Jednym z głównych odniesień wykorzystywanych przez amerykańskich planistów jest Podręcznik przepustowości autostrad , opublikowany przez Radę ds. Badań nad Transportem , która jest częścią Narodowej Akademii Nauk Stanów Zjednoczonych . Zaleca się modelowanie przepływów ruchu z wykorzystaniem całego czasu podróży przez łącze za pomocą funkcji opóźnienia/przepływu, w tym skutków kolejkowania. Technika ta jest wykorzystywana w wielu modelach ruchu w USA oraz w modelu SATURN w Europie.

W wielu częściach Europy stosuje się hybrydowe podejście empiryczne do projektowania ruchu, łączące cechy makro-, mikro- i mezoskopowe. Zamiast symulować stan ustalony przepływu na trasie, symulowane są przejściowe „szczyty popytu” zatorów komunikacyjnych. Są one modelowane przy użyciu małych „wycinków czasu” w sieci w ciągu dnia roboczego lub weekendu. Zazwyczaj miejsca początkowe i docelowe podróży są najpierw szacowane, a model ruchu jest generowany przed kalibracją poprzez porównanie modelu matematycznego z zaobserwowanymi liczbami rzeczywistych przepływów ruchu, sklasyfikowanych według typu pojazdu. Następnie do modelu stosuje się „oszacowanie macierzowe”, aby uzyskać lepsze dopasowanie do zaobserwowanej liczby linków przed wprowadzeniem jakichkolwiek zmian, a poprawiony model jest używany do wygenerowania bardziej realistycznej prognozy ruchu dla każdego proponowanego schematu. Model byłby uruchamiany kilka razy (w tym bieżący poziom bazowy, prognoza „średniego dnia” oparta na szeregu parametrów ekonomicznych i poparta analizą wrażliwości) w celu zrozumienia skutków tymczasowych blokad lub incydentów w sieci. Z modeli można zsumować czas potrzebny wszystkim kierowcom różnych typów pojazdów w sieci, a tym samym wywnioskować średnie zużycie paliwa i emisje.

Wiele praktyk władz brytyjskich, skandynawskich i holenderskich polega na wykorzystaniu programu do modelowania CONTRAM dla dużych projektów, który był rozwijany przez kilka dziesięcioleci pod auspicjami brytyjskiego Transport Research Laboratory, a ostatnio przy wsparciu szwedzkiej administracji drogowej . Modelując prognozy sieci drogowej na kilkadziesiąt lat w przyszłość, można obliczyć korzyści ekonomiczne zmian w sieci drogowej, wykorzystując szacunki wartości czasu i innych parametrów. Dane wyjściowe tych modeli można następnie wprowadzić do programu analizy kosztów i korzyści.

Skumulowane krzywe liczby pojazdów ( N -krzywe)

Krzywa skumulowanej liczby pojazdów, krzywa N , przedstawia skumulowaną liczbę pojazdów, które przejeżdżają przez określoną lokalizację x w czasie t , mierzonym od przejazdu jakiegoś pojazdu referencyjnego. Krzywą tę można wykreślić, jeśli znane są czasy przybycia poszczególnych pojazdów zbliżających się do lokalizacji x , a czasy odjazdu są również znane, gdy opuszczają one lokalizację x . Uzyskanie tych czasów przyjazdu i odjazdu może wiązać się z gromadzeniem danych: na przykład można ustawić dwa czujniki punktowe w lokalizacjach X ₁ i X ₂ i policz liczbę pojazdów, które przejeżdżają przez ten segment, jednocześnie rejestrując czas, w którym każdy pojazd przybywa do X ₁ i odjeżdża z X ₂ . Otrzymany wykres jest parą krzywych skumulowanych, gdzie oś pionowa ( N ) przedstawia skumulowaną liczbę pojazdów, które przejeżdżają przez dwa punkty: X ₁ i X ₂ , a oś pozioma ( t ) reprezentuje czas, jaki upłynął od X ₁ i X ₂ .

Rysunek 8. Proste krzywe skumulowane

Rysunek 9. Krzywe przyjazdu, wirtualnego przyjazdu i wyjazdu

Jeśli pojazdy nie doświadczają żadnych opóźnień podczas podróży z X ₁ do X ₂ , to przyjazdy pojazdów do lokalizacji X ₁ są reprezentowane przez krzywą N ₁ , a przyjazdy pojazdów do lokalizacji X ₂ są reprezentowane przez N ₂ na rysunku 8. Więcej zwykle krzywa N ₁ jest znana jako krzywa przybycia pojazdów do lokalizacji X ₁ , a krzywa N ₂ jest znana jako krzywa przybycia pojazdów do lokalizacji X ₂ . Używając jako przykładu jednopasmowego wjazdu do skrzyżowania z sygnalizacją świetlną, gdzie X ₁ to położenie poprzeczki zatrzymania na wjeździe, a X ₂ to dowolna linia na pasie docelowym po drugiej stronie skrzyżowania, kiedy sygnalizacja świetlna jest zielona , pojazdy mogą przejechać przez oba punkty bez opóźnień, a czas potrzebny na pokonanie tej odległości jest równy czasowi podróży w swobodnym przepływie. Graficznie jest to pokazane jako dwie oddzielne krzywe na rysunku 8.

Jednakże, gdy sygnalizacja świetlna jest czerwona, pojazdy docierają do słupka zatrzymania ( X ₁ ) i są opóźniane przez czerwone światło przed przekroczeniem X ₂ jakiś czas po zmianie sygnału na zielony. W rezultacie na skrzyżowaniu tworzy się kolejka, ponieważ coraz więcej pojazdów przybywa na skrzyżowanie, podczas gdy sygnalizacja świetlna jest nadal czerwona. _{Zatem tak długo, jak pojazdy}_{przybywające} do skrzyżowania są nadal zatrzymywane przez kolejkę, krzywa N2 nie przedstawia już przybycia pojazdów do miejsca X2 ; reprezentuje teraz wirtualne przybycie pojazdów w lokalizacji X ₂ , czyli innymi słowy reprezentuje przybycie pojazdów do X _{2 ,} jeśli nie doświadczyły żadnego opóźnienia. Przybycie pojazdów do lokalizacji X ₂ , z uwzględnieniem opóźnienia spowodowanego sygnalizacją świetlną, jest teraz reprezentowane przez krzywą N' ₂ na rysunku 9.

Jednak koncepcja krzywej wirtualnego przybycia jest błędna. Krzywa ta nie przedstawia poprawnie długości kolejki wynikającej z przerwy w ruchu (tj. sygnału czerwonego). Zakłada się, że wszystkie pojazdy wciąż docierają do poprzeczki, zanim zostaną opóźnione przez czerwone światło. Innymi słowy, krzywa wirtualnego przybycia przedstawia pionowe układanie pojazdów na pasku zatrzymania. Kiedy sygnalizacja świetlna zmienia kolor na zielony, pojazdy te są obsługiwane w kolejności FIFO (first in first first out). Jednak w przypadku podejścia wielopasmowego zlecenie serwisowe niekoniecznie jest FIFO. Niemniej jednak interpretacja jest nadal użyteczna ze względu na uwzględnienie średniego całkowitego opóźnienia zamiast całkowitych opóźnień dla poszczególnych pojazdów.

Funkcja krokowa a funkcja gładka

Rysunek 10. Funkcja schodkowa

Przykład sygnalizacji świetlnej przedstawia N -krzywe jako gładkie funkcje. Teoretycznie jednak wykreślenie N -krzywych z zebranych danych powinno skutkować funkcją schodkową (rysunek 10). Każdy krok reprezentuje przybycie lub odjazd jednego pojazdu w tym momencie. Kiedy N zostanie narysowana w większej skali, odzwierciedlającej okres czasu obejmujący kilka cykli, wówczas kroki dla poszczególnych pojazdów można zignorować, a krzywa będzie wyglądać jak płynna funkcja (rysunek 8).

Przydział ruchu

Rysunek 14. Czterostopniowy model zapotrzebowania na podróż dla przydziału ruchu

Celem analizy potoków ruchu jest stworzenie i wdrożenie modelu, który umożliwiłby pojazdom dotarcie do celu w jak najkrótszym czasie przy wykorzystaniu maksymalnej przepustowości jezdni. Jest to czteroetapowy proces:

Generacja – program szacuje, ile przejazdów zostałoby wygenerowanych. W tym celu program potrzebuje danych statystycznych dotyczących obszarów zamieszkania według ludności, lokalizacji miejsc pracy itp.;
Dystrybucja – po wygenerowaniu tworzy różne pary Origin-Destination (OD) między lokalizacją znalezioną w kroku 1;
Modal Split/Mode Choice – system musi zdecydować, jaki procent populacji zostanie podzielony między różne dostępne środki transportu, np. samochody, autobusy, koleje itp.;
Przypisanie trasy – wreszcie trasy są przydzielane pojazdom na podstawie minimalnych kryteriów.

Ten cykl jest powtarzany, aż rozwiązanie będzie zbieżne.

Istnieją dwa główne podejścia do rozwiązania tego problemu wraz z celami końcowymi:

Optymalny system

Krótko mówiąc, sieć jest optymalna dla systemu (SO), gdy całkowity koszt systemu jest najniższy spośród wszystkich możliwych przypisań.

System Optimum opiera się na założeniu, że trasy wszystkich pojazdów będą kontrolowane przez system, a zmiana tras będzie oparta na maksymalnym wykorzystaniu zasobów i minimalnym całkowitym koszcie systemu. (Koszt można zinterpretować jako czas podróży). Dlatego w algorytmie trasowania optymalnego dla systemu wszystkie trasy między daną parą OD mają ten sam koszt krańcowy. W tradycyjnej ekonomii transportu optymalny system jest określany przez funkcję równowagi popytu i funkcję kosztów krańcowych. W tym podejściu koszt krańcowy jest z grubsza przedstawiany jako rosnąca funkcja w zatłoczeniu ruchu. W podejściu do przepływu ruchu koszt krańcowy podróży można wyrazić jako sumę kosztów (czas opóźnienia, w ) doświadczane przez kierowcę oraz efekty zewnętrzne ( e ), które kierowca nakłada na pozostałych użytkowników.

₀₀ Załóżmy, że istnieje autostrada (0) i trasa alternatywna (1), którą użytkownicy mogą skierować na zjazd. Operator zna całkowity wskaźnik przyjazdu ( A ( t )), przepustowość autostrady ( μ ) oraz przepustowość trasy alternatywnej ( μ ₁ ). Od momentu „t ”, kiedy autostrada jest zatłoczona, część użytkowników zaczyna przemieszczać się na trasę alternatywną. Jednak gdy t ₁ , trasa alternatywna jest również pełna przepustowości. Teraz operator decyduje o liczbie pojazdów (N), które korzystają z trasy alternatywnej. Optymalna liczba pojazdów ( N ₀ ) można uzyskać za pomocą rachunku zmienności, aby zrównać koszt krańcowy każdej trasy. Zatem optymalnym warunkiem jest T = T ₁ + ∆ ₁ . Na tym wykresie widać, że kolejka na trasie alternatywnej powinna przejechać ∆ ₁ jednostek czasu, zanim opuści autostradę. To rozwiązanie nie definiuje, w jaki sposób powinniśmy przydzielać pojazdy przyjeżdżające między t ₁ a T ₁ , możemy jedynie stwierdzić, że rozwiązanie optymalne nie jest jednoznaczne. Jeśli operator chce, aby autostrada nie była zatłoczona, może nałożyć opłatę za zator, ₀ e ― e ₁ , czyli różnica między efektem zewnętrznym autostrady i trasy alternatywnej. W tej sytuacji autostrada utrzyma prędkość swobodnego ruchu, jednak trasa alternatywna będzie bardzo zatłoczona.

Równowaga użytkownika

W skrócie, sieć znajduje się w równowadze użytkownika (UE), gdy każdy kierowca wybiera trasy o najniższym koszcie między punktem początkowym a docelowym, niezależnie od tego, czy całkowity koszt systemu jest zminimalizowany.

Optymalna równowaga użytkownika zakłada, że wszyscy użytkownicy wybierają własną trasę do miejsca docelowego na podstawie czasu podróży, który zostanie zużyty w różnych wariantach trasy. Użytkownicy wybiorą trasę, która wymaga najmniejszego czasu przejazdu. Model optymalny dla użytkownika jest często używany do symulacji wpływu wąskich gardeł na autostradzie na przydział ruchu. Kiedy zator pojawi się na autostradzie, wydłuży to czas opóźnienia w podróży przez autostradę i wydłuży czas podróży. Przy założeniu optymalnego użytkownika użytkownicy zdecydowaliby się poczekać, aż czas przejazdu określoną autostradą zrówna się z czasem przejazdu ulicami miasta, a tym samym zostanie osiągnięta równowaga. Ta równowaga nazywana jest równowagą użytkownika, równowagą Wardropa lub równowagą Nasha.

Rysunek 15. Model ruchu równowagi użytkownika

Podstawową zasadą User Equilibrium jest to, że wszystkie używane trasy między daną parą OD mają taki sam czas podróży. Opcja trasy alternatywnej jest dostępna do użycia, gdy rzeczywisty czas podróży w systemie osiągnął czas podróży swobodnej na tej trasie.

Dla optymalnego modelu użytkownika autostrady uwzględniającego jedną alternatywną trasę, typowy proces przydzielania ruchu pokazano na rysunku 15. Kiedy zapotrzebowanie na ruch pozostaje poniżej przepustowości autostrady, czas opóźnienia na autostradzie pozostaje zerowy. Gdy zapotrzebowanie ruchu przekroczy przepustowość, na autostradzie pojawi się kolejka pojazdów, a czas opóźnienia wzrośnie. Niektórzy użytkownicy zwrócą się na ulice miasta, gdy czas opóźnienia osiągnie różnicę między czasem swobodnego przejazdu autostradą a czasem swobodnego przejazdu ulicami miasta. Wskazuje to, że użytkownicy przebywający na autostradzie spędzą w podróży tyle samo czasu, co ci, którzy skierują się na ulice miasta. Na tym etapie czas przejazdu zarówno autostradą, jak i trasą alternatywną pozostaje taki sam. Sytuację tę można zakończyć, gdy popyt spadnie poniżej przepustowości dróg, czyli czas przejazdu autostradą zacznie się skracać i wszyscy użytkownicy pozostaną na autostradzie. Suma części obszaru 1 i 3 przedstawia korzyści wynikające z zapewnienia alternatywnej trasy. Suma obszaru 4 i obszaru 2 pokazuje całkowity koszt opóźnienia w systemie, gdzie obszar 4 to całkowite opóźnienie występujące na autostradzie, a obszar 2 to dodatkowe opóźnienie spowodowane przeniesieniem ruchu na ulice miasta.

Funkcję nawigacji w Mapach Google można określić jako typową przemysłową aplikację dynamicznego przydzielania ruchu w oparciu o User Equilibrium, ponieważ zapewnia ona każdemu użytkownikowi opcję wyznaczania trasy przy jak najniższym koszcie (czasie podróży).

Opóźnienie

Zarówno User Optimum, jak i System Optimum można podzielić na dwie kategorie na podstawie podejścia do opóźnienia czasowego przyjętego dla ich rozwiązania:

Predykcyjne opóźnienie czasowe

Predykcyjne opóźnienie czasowe zakłada, że użytkownik systemu dokładnie wie, jak długie będzie opóźnienie. Predykcyjne opóźnienie wie, kiedy zostanie osiągnięty określony poziom zatoru i kiedy opóźnienie tego systemu byłoby większe niż zabranie innego systemu, więc decyzja o zmianie trasy może zostać podjęta na czas. Na wykresie zliczeń pojazdów w funkcji czasu przewidywane opóźnienie w czasie t jest poziomym odcinkiem linii po prawej stronie czasu t, między krzywą przyjazdu i wyjazdu, pokazaną na rysunku 16. Odpowiednia współrzędna y to numer n-tego pojazdu, który opuszcza system w czasie t.

Reaktywne opóźnienie czasowe

Reaktywne opóźnienie czasowe ma miejsce, gdy użytkownik nie ma wiedzy o warunkach drogowych z przodu. Użytkownik czeka, aby doświadczyć punktu, w którym zaobserwowano opóźnienie, a decyzja o zmianie trasy jest reakcją na to doświadczenie w danym momencie. Opóźnienie predykcyjne daje znacznie lepsze wyniki niż metoda opóźnienia reaktywnego. Na wykresie zliczeń pojazdów w funkcji czasu przewidywane opóźnienie w czasie t jest poziomym odcinkiem linii po lewej stronie czasu t, między krzywą przyjazdu i wyjazdu, pokazaną na rysunku 16. Odpowiednia współrzędna y to numer n-tego pojazdu, który wjeżdża do systemu w czasie t.

Rysunek 16. Predykcyjne i reaktywne opóźnienie czasowe

Zmienne przypisanie ograniczenia prędkości

To nadchodzące podejście do eliminacji fali uderzeniowej i zwiększenia bezpieczeństwa pojazdów. Koncepcja opiera się na fakcie, że ryzyko wypadku na jezdni wzrasta wraz z różnicą prędkości między pojazdami poprzedzającymi i jadącymi z prądem. Dwa rodzaje ryzyka zderzenia, które można zmniejszyć dzięki wdrożeniu VSL, to uderzenie w tył pojazdu i zderzenie podczas zmiany pasa ruchu. Zmienne ograniczenia prędkości mają na celu ujednolicenie prędkości, co prowadzi do bardziej stałego przepływu. Badacze zastosowali różne podejścia w celu zbudowania odpowiedniego algorytmu VSL.

Zmienne ograniczenia prędkości są zwykle wprowadzane, gdy czujniki wzdłuż jezdni wykryją, że zatory lub zdarzenia pogodowe przekroczyły progi. Ograniczenie prędkości na jezdni zostanie następnie zmniejszone w krokach co 5 mil na godzinę za pomocą znaków nad jezdnią (Dynamic Message Signs) kontrolowanych przez Departament Transportu. Celem tego procesu jest zarówno zwiększenie bezpieczeństwa poprzez zmniejszenie liczby wypadków, jak i uniknięcie lub opóźnienie powstania zatorów na jezdni. Idealny wynikający z tego przepływ ruchu jest ogólnie wolniejszy, ale mniej zatrzymywania się i ruszania, co skutkuje mniejszą liczbą wypadków związanych z najechaniem na tył pojazdu i wypadkami przy zmianie pasa ruchu. Korzystanie z VSL również regularnie wykorzystuje pobocza dozwolone dla transportu tylko w stanach zatłoczenia, z którymi ten proces ma na celu zwalczanie. Potrzeba zmiennego ograniczenia prędkości jest pokazana na wykresie Flow-Density po prawej stronie.

Diagram prędkości i przepływu dla typowej jezdni

Na tym rysunku („Wykres przepływu i prędkości dla typowej jezdni”) punkt krzywej reprezentuje optymalny ruch drogowy zarówno pod względem przepływu, jak i prędkości. Jednak poza tym punktem prędkość podróży szybko osiąga próg i zaczyna gwałtownie spadać. Aby zmniejszyć potencjalne ryzyko tego gwałtownego spadku prędkości, zmienne ograniczenia prędkości zmniejszają prędkość w bardziej stopniowym tempie (co 5 mil na godzinę), dając kierowcom więcej czasu na przygotowanie się i przystosowanie do spowolnienia spowodowanego korkami/pogodą. Rozwój jednolitej prędkości jazdy zmniejsza prawdopodobieństwo nieobliczalnego zachowania kierowcy, a tym samym wypadków.

Na podstawie danych historycznych uzyskanych na obiektach VSL ustalono, że wdrożenie tej praktyki zmniejsza liczbę wypadków o 20-30%.

Oprócz kwestii związanych z bezpieczeństwem i wydajnością, VSL mogą również przynosić korzyści dla środowiska, takie jak zmniejszona emisja, hałas i zużycie paliwa. Wynika to z faktu, że pojazdy zużywają mniej paliwa, gdy poruszają się ze stałą prędkością, a nie w stanie stałego przyspieszania i zwalniania, jak zwykle w zatłoczonych warunkach.

Węzły drogowe

Ważnym elementem przepustowości dróg jest projektowanie skrzyżowań. Pozwalając na długie „splatające się odcinki” na łagodnie zakrzywionych drogach na stopniowanych skrzyżowaniach, pojazdy często mogą poruszać się po pasach bez powodowania znacznych zakłóceń w ruchu. Jest to jednak kosztowne i zajmuje dużo miejsca, dlatego często stosuje się inne wzory, szczególnie na obszarach miejskich lub bardzo wiejskich. Większość dużych modeli wykorzystuje prymitywne symulacje skrzyżowań, ale dostępne są symulacje komputerowe do modelowania określonych zestawów sygnalizacji świetlnej, rond i innych scenariuszy, w których przepływ jest przerywany lub współdzielony z innymi typami użytkowników dróg lub pieszych. Dobrze zaprojektowane skrzyżowanie może zapewnić znacznie większy przepływ ruchu w ciągu dnia przy różnym natężeniu ruchu. Dopasowując taki model do „Inteligentnego Systemu Transportowego”, ruch może być wysyłany w nieprzerwanych „pakietach” pojazdów z określoną prędkością przez szereg fazowanych sygnalizacji świetlnych. Wielkiej Brytanii TRL opracował programy do modelowania skrzyżowań dla lokalnych schematów na małą skalę, które mogą uwzględniać szczegółową geometrię i linie wzroku; ARCADY dla rond, PICADY dla skrzyżowań z priorytetem oraz OSCADY i TRANSYT dla sygnałów. Istnieje wiele innych pakietów oprogramowania do analizy połączeń, takich jak Sidra , LinSig i Synchro.

Model fali kinematycznej

Model fali kinematycznej został po raz pierwszy zastosowany do przepływu ruchu przez Lighthilla i Whithama w 1955 roku. Ich dwuczęściowy artykuł jako pierwszy rozwinął teorię fal kinematycznych na przykładzie ruchu wody. W drugiej połowie rozszerzyli teorię na ruch na „zatłoczonych arteriach”. Ten artykuł dotyczył przede wszystkim rozwinięcia koncepcji „garbów” (zwiększenia przepływu) i ich wpływu na prędkość, zwłaszcza w przypadku wąskich gardeł.

Autorzy rozpoczęli od omówienia wcześniejszych podejść do teorii przepływu ruchu. Zauważają, że w tamtym czasie prowadzono pewne prace eksperymentalne, ale „teoretyczne podejście do tematu [było] w powijakach”. W szczególności jeden badacz, John Glen Wardrop, zajmował się przede wszystkim statystycznymi metodami badania, takimi jak średnia prędkość w przestrzeni, średnia prędkość w czasie oraz „wpływ zwiększenia przepływu na wyprzedzanie” i wynikające z tego zmniejszenie prędkości. Inne wcześniejsze badania koncentrowały się na dwóch oddzielnych modelach: jeden dotyczył prędkości ruchu drogowego z natężeniem ruchu, a drugi dotyczył prędkości ruchu między pojazdami.

Z drugiej strony celem Lighthilla i Whithama było zaproponowanie nowej metody badawczej „sugerowanej przez teorie przepływu dotyczące pocisków naddźwiękowych i ruchu powodziowego w rzekach”. Powstały model uchwyciłby obie wyżej wymienione zależności, prędkość-przepływ i prędkość-postęp, w jednej krzywej, która „[podsumowałaby] wszystkie właściwości odcinka drogi, które są istotne dla jego zdolności do obsługi przepływu zatłoczony ruch”. Przedstawiony przez nich model powiązał natężenie ruchu z koncentracją (obecnie zwykle określaną jako gęstość). Napisali: „Podstawową hipotezą tej teorii jest to, że w dowolnym punkcie drogi przepływ q (pojazdów na godzinę) jest funkcją koncentracji k (pojazdów na milę)”. Zgodnie z tym modelem przepływ ruchu przypominał przepływ wody w tym sensie, że „Niewielkie zmiany przepływu są propagowane z powrotem przez strumień pojazdów wzdłuż 'fal kinematycznych', których prędkość względem drogi jest nachyleniem wykresu przepływu w funkcji koncentracji. ” Autorzy zamieścili przykład takiego wykresu; ten wykres przepływu w zależności od stężenia (gęstości) jest nadal używany (patrz rysunek 3 powyżej).

Autorzy wykorzystali ten model koncentracji przepływu, aby zilustrować koncepcję fal uderzeniowych, które spowalniają wjeżdżające w nie pojazdy oraz warunki, które je otaczają. Omówili również wąskie gardła i skrzyżowania, odnoszące się do ich nowego modelu. Dla każdego z tych tematów uwzględniono diagramy przepływu-stężenia i czasoprzestrzeni. Na koniec autorzy zauważyli, że nie istnieje żadna uzgodniona definicja przepustowości i argumentowali, że należy ją zdefiniować jako „maksymalny przepływ, do którego zdolna jest droga”. Lighthill i Whitham zauważyli również, że ich model miał istotne ograniczenia: nadawał się tylko do użytku na długich, zatłoczonych drogach, ponieważ podejście „ciągłego przepływu” sprawdza się tylko w przypadku dużej liczby pojazdów.

Elementy falowego modelu kinematycznego teorii potoków ruchu

Kinematyczny model falowy teorii przepływu ruchu jest najprostszym dynamicznym modelem przepływu ruchu, który odtwarza propagację fal ruchu . Składa się z trzech elementów: diagramu podstawowego , równania zachowania i warunków początkowych. Podstawowym prawem rządzącym modelem fali kinematycznej jest prawo zachowania:

${\ Displaystyle {\ Frac {\ częściowe k} {\ częściowe t}} + {\ Frac {\ częściowe q} {\ częściowe x}} = 0,}$

Podstawowy diagram modelu fali kinematycznej wiąże przepływ ruchu z gęstością, jak pokazano na rysunku 3 powyżej. Można to zapisać jako:

${\ Displaystyle {q} = {F (k)}}$

Na koniec należy zdefiniować warunki początkowe, aby rozwiązać problem za pomocą modelu. Granica jest zdefiniowana jako $gęstość$ i Granice te zwykle przybierają dwie różne formy, co skutkuje problemami z wartością początkową (IVP) i problemami z wartością graniczną (BVP). Problemy z wartością początkową dają gęstość ruchu w czasie ${\ displaystyle {t} = {0}}$ , takie, że gdzie $Displaystyle {g (x)}}$ $x )$ jest daną funkcją gęstości Problemy z wartościami granicznymi dają pewną funkcję $,$ ${\ Displaystyle {k (t, 0)} = {g (t)}}$ $t$ pozycji , . Model ma wiele zastosowań w przepływie ruchu. Jednym z podstawowych zastosowań jest modelowanie wąskich gardeł ruchu, jak opisano w następnej sekcji.

Wąskie gardło w ruchu

Wąskie gardła w ruchu to zakłócenia w ruchu na jezdni spowodowane przez projekt drogi, sygnalizację świetlną lub wypadki. Istnieją dwa ogólne rodzaje wąskich gardeł, stacjonarne i ruchome wąskie gardła. Stacjonarne wąskie gardła to te, które powstają w wyniku zakłócenia występującego w wyniku stacjonarnej sytuacji, takiej jak zwężenie jezdni, wypadek. Z drugiej strony ruchome wąskie gardła to te pojazdy lub zachowania pojazdów, które powodują zakłócenia w pojazdach znajdujących się przed pojazdem. Generalnie wąskie gardła w ruchu są powodowane przez ciężkie samochody ciężarowe, ponieważ są to pojazdy wolno poruszające się z mniejszym przyspieszeniem, a także mogą powodować zmiany pasa ruchu.7

Przyczyny korków w Stanach Zjednoczonych

Wąskie gardła (40%)

Zdarzenia drogowe (25%)

Strefy pracy (10%)

Zła pogoda (15%)

Słabe taktowanie sygnału (5%)

Wydarzenia specjalne / inne (5%)

Wąskie gardła to ważne kwestie, ponieważ wpływają na płynność ruchu i średnie prędkości pojazdów. Główną konsekwencją zatoru jest natychmiastowe zmniejszenie przepustowości jezdni. Federalny Urząd ds. Autostrad stwierdził, że 40% wszystkich zatorów wynika z wąskich gardeł. ^{[ potrzebne źródło ]}

Stacjonarne wąskie gardło

Rysunek 18

Ogólną przyczyną stacjonarnych wąskich gardeł są spadki pasa ruchu, które występują, gdy wielopasmowa jezdnia traci jeden lub więcej pasów ruchu. Powoduje to, że ruch kołowy na końcowych pasach łączy się z innymi pasami.

Ruchome wąskie gardło

Jak wyjaśniono powyżej, ruchome wąskie gardła są spowodowane przez wolno poruszające się pojazdy, które powodują zakłócenia w ruchu. Ruchome wąskie gardła mogą być aktywnymi lub nieaktywnymi wąskimi gardłami. Jeżeli zmniejszona przepustowość (qu ₎ spowodowana poruszającym się wąskim gardłem jest większa niż rzeczywista przepustowość (μ) za pojazdem, wówczas mówi się, że to wąskie gardło jest wąskim gardłem aktywnym.

Klasyczne teorie przepływu ruchu

Ogólnie przyjęte klasyczne podstawy i metodologie teorii ruchu i transportu są następujące:

Model Lighthill-Whitham-Richards (LWR) wprowadzony w latach 1955–56. Daganzo wprowadził model transmisji komórkowej (CTM), który jest zgodny z modelem LWR.
Niestabilność potoku ruchu powodująca narastającą falę lokalnego zmniejszenia prędkości pojazdów. Ta klasyczna niestabilność przepływu ruchu została wprowadzona w latach 1959–61 w modelu podążania za samochodem General Motors (GM) przez Hermana, Gazisa, Montrolla, Pottsa i Rothery'ego. Klasyczna niestabilność przepływu ruchu w modelu GM została uwzględniona w ogromnej liczbie modeli przepływu ruchu, takich jak model Gippsa, model Payne'a, model optymalnej prędkości (OV) Newella, model Wiedemanna, model Whithama, automat komórkowy Nagel-Schreckenberg (NaSch) (CA), Bando i in. model OV, IDM Treibera, model Kraußa, model Aw-Rascle i wiele innych znanych mikroskopowych i makroskopowych modeli potoków ruchu, które są podstawą do symulacji ruchu szeroko stosowane przez inżynierów i badaczy ruchu (patrz np. przegląd literatury).
Rozumienie przepustowości autostrady jako szczególnej wartości. Takie rozumienie przepustowości dróg zostało prawdopodobnie wprowadzone w latach 1920–35 (patrz ). Obecnie przyjmuje się, że przepustowość autostrady przy wąskim gardle autostrady jest wartością stochastyczną. Jednak zgodnie z klasycznym rozumieniem przepustowości autostrady przyjmuje się, że w danej chwili czasowej może istnieć tylko jedna konkretna wartość tej stochastycznej przepustowości autostrady (patrz literatura w książce).
Zasady równowagi użytkownika (UE) i optymalnego systemu (SO) Wardrop dla optymalizacji i kontroli ruchu i sieci transportowej.

Alternatywy: trójfazowa teoria ruchu Kernera

Teoria ruchu trójfazowego jest alternatywną teorią przepływu ruchu, stworzoną przez Borisa Kernera pod koniec lat 90. (przeglądy w książkach). Prawdopodobnie najważniejszym rezultatem teorii trójfazowej jest to, że w każdej chwili istnieje zakres przepustowości autostrady swobodnego przepływu w wąskim gardle. Zakres wydajności mieści się między pewnymi maksymalnymi i minimalnymi wydajnościami. Zakres przepustowości autostrady swobodnego przepływu w wąskim gardle w teorii ruchu trójfazowego zaprzecza zasadniczo klasycznym teoriom ruchu, a także metodom zarządzania ruchem i sterowania ruchem, które w każdej chwili zakładają istnienie szczególną deterministyczną lub stochastyczną przepustowość autostrady w przypadku wąskiego gardła. Osoby niebędące specjalistami, które nigdy wcześniej nie miały styczności ze zjawiskami drogowymi, mogą znaleźć w książce uproszczone wyjaśnienia rzeczywistych, mierzonych zjawisk drogowych prowadzących do powstania trójfazowej teorii ruchu Kernera; w książce można znaleźć niektóre zastosowania inżynierskie teorii Kernera.

Modele scalania Newella-Daganzo

Diagram modelu scalania Newella-Daganzo i jego zmienne

W warunkach potoków opuszczających dwa rozgałęzienia i łączących się w jeden ciąg przez jedną jezdnię, określenie potoków przechodzących przez proces łączenia oraz stanu poszczególnych rozgałęzień staje się ważnym zadaniem dla inżynierów ruchu. Model scalania Newella -Daganzo jest dobrym podejściem do rozwiązania tych problemów. Ten prosty model jest wynikiem zarówno opisu procesu łączenia przez Gordona Newella, jak i modelu transmisji komórkowej Daganzo . Aby zastosować model do wyznaczenia potoków wychodzących z dwóch odgałęzień oraz statystyki każdego z odgałęzień, należy znać przepustowość dwóch wejściowych odgałęzień, przepustowość zjazdową, zapotrzebowanie dla każdego z odgałęzień oraz liczbę pasów ruchu na jednej jezdni. Współczynnik scalania zostanie obliczony w celu określenia proporcji dwóch przepływów wejściowych, gdy oba odgałęzienia jezdni poruszają się w warunkach zatoru.

Jak widać na uproszczonym modelu procesu scalania, wyjściowa przepustowość układu jest określona jako μ, przepustowość dwóch wejściowych odgałęzień jezdni jako μ 1 i μ 2 , a _{zapotrzebowanie} dla _każdego odgałęzienia jezdni definiuje się jako q ₁^D i q ₂^D . q ₁ i q ₂ są danymi wyjściowymi modelu, które są przepływami przechodzącymi przez proces łączenia. Proces modelu opiera się na założeniu, że suma przepustowości dwóch gałęzi wejściowych jezdni jest mniejsza od przepustowości wyjściowej systemu, μ ₁ + μ ₂ ≤ μ.

Modele podążające za samochodami

Modele podążania za samochodem opisują, w jaki sposób jeden pojazd podąża za innym pojazdem w nieprzerwanym ruchu drogowym. Są rodzajem mikroskopijnego modelu przepływu ruchu .

Przykłady modeli podążających za samochodami

Model podążający za samochodem Newella
Louis A. Pipes zaczął badać i zdobywać uznanie opinii publicznej na początku lat pięćdziesiątych. Model podążania za samochodem Pipesa oparty jest na zasadzie bezpiecznej jazdy zawartej w kalifornijskim kodeksie pojazdów silnikowych, a model ten wykorzystuje założenie bezpiecznej odległości: dobrą zasadą podążania za innym pojazdem jest wyznaczenie odległości między pojazdami co najmniej równej długości samochód na każde dziesięć mil na godzinę prędkości pojazdu. M
Aby uchwycić potencjalne efekty nieliniowe w dynamice podążania za samochodem, GF Newell zaproponował nieliniowy model podążania za samochodem oparty na danych empirycznych. W przeciwieństwie do modelu Pipesa, który opiera się wyłącznie na zasadach bezpiecznej jazdy, nieliniowy model Newella ma na celu uchwycenie prawidłowego kształtu podstawowych diagramów (np. ).
Model optymalnej prędkości (OVM) został wprowadzony przez Bando i in. w 1995 r. przy założeniu, że każdy kierowca stara się osiągnąć optymalną prędkość zgodnie z różnicą między pojazdami i różnicą prędkości między pojazdami poprzedzającymi.
Model inteligentnego kierowcy jest szeroko stosowany w badaniach pojazdów połączonych (CV) oraz pojazdów połączonych i autonomicznych (CAV).

Zobacz też

Dalsza lektura

Ankieta na temat stanu techniki w modelowaniu przepływu ruchu:

N. Bellomo, V. Coscia, M. Delitala, O matematycznej teorii przepływu ruchu kołowego I. Dynamiczne i kinetyczne modelowanie płynów, Math. mod. met. Aplikacja. Sc. , Tom. 12, nr 12 (2002) 1801–1843
S. Maerivoet, Modelowanie ruchu na autostradach: najnowocześniejsza analiza danych numerycznych i dynamiczne wyznaczanie ruchu , Katholieke Universiteit Leuven, 2006
M. Garavello i B. Piccoli, Przepływ ruchu w sieciach, American Institute of Mathematical Sciences (AIMS), Springfield, MO, 2006. s. xvi+243 ISBN 978-1-60133-000-0
Carlos F. Daganzo, „Podstawy transportu i operacji drogowych”, Pergamon-Elsevier, Oxford, Wielka Brytania (1997)
BS Kerner, Wprowadzenie do współczesnej teorii przepływu ruchu i sterowania: długa droga do trójfazowej teorii ruchu , Springer, Berlin, Nowy Jork 2009
Cassidy, MJ i RL Bertini. „Obserwacje w wąskim gardle autostrady”. Teoria transportu i ruchu (1999).
Daganzo, Carlos F. „Prosta procedura analizy ruchu”. Sieci i ekonomia przestrzenna 1.i (2001): 77–101.
Lindgren, Roger VF „Analiza funkcji przepływu w ruchu w kolejce na niemieckiej autostradzie”. Uniwersytet Stanowy w Portland (2005).
Ni, B. i JD Leonard. „Bezpośrednie metody określania charakterystyki strumienia ruchu według definicji”. Rekord badań transportu (2006).

Książki przydatne z fizycznego punktu widzenia:

M. Treiber i A. Kesting, „Dynamika przepływu ruchu”, Springer, 2013
BS Kerner, Fizyka ruchu drogowego , Springer, Berlin, Nowy Jork 2004
Przepływ ruchu na arxiv.org
maja, Adolfie. Podstawy przepływu ruchu . Prentice Hall, Englewood Cliffs, NJ, 1990.
Taylor, Mikołaj. Dynamiczny model przydziału ruchu Contram TRL 2003

Linki zewnętrzne

Piąte wydanie Podręcznika dotyczącego przepustowości autostrad (HCM 2010) wydane przez Transportation Research Board (TRB)