Rachunkowość wzrostu

Rachunek wzrostu to procedura stosowana w ekonomii do pomiaru udziału różnych czynników we wzroście gospodarczym i pośredniego obliczania tempa postępu technologicznego, mierzonego jako pozostałość, w gospodarce. Rachunkowość wzrostu rozkłada stopę wzrostu całkowitej produkcji gospodarki na tę, która jest spowodowana wzrostem udziału zastosowanych czynników - zwykle wzrostem ilości kapitału i pracy — oraz tego, czego nie można wytłumaczyć obserwowalnymi zmianami w wykorzystaniu czynników produkcji. Następnie przyjmuje się, że niewyjaśniona część wzrostu PKB reprezentuje wzrost produktywności (uzyskanie większej produkcji przy tych samych nakładach) lub miarę szeroko rozumianego postępu technologicznego.

Technika ta została zastosowana do praktycznie każdej gospodarki na świecie i powszechnie stwierdza się, że obserwowanych poziomów wzrostu gospodarczego nie można wytłumaczyć po prostu zmianami w zasobach kapitału w gospodarce lub tempem wzrostu liczby ludności i siły roboczej. Stąd postęp technologiczny odgrywa kluczową rolę we wzroście gospodarczym narodów lub jego braku.

Historia

Metodologia ta została wprowadzona przez Roberta Solowa i Trevora Swana w 1957 r. Rachunkowość wzrostu została zaproponowana do rachunkowości zarządczej w latach 80. XX wieku. ale nie zyskały na znaczeniu jako narzędzia zarządzania. Powód jest jasny. Funkcje produkcji są różnie rozumiane i formułowane w rachunkowości wzrostu i rachunkowości zarządczej. W rachunku wzrostu funkcja produkcji jest formułowana jako funkcja WYJŚCIE=F (WEJŚCIE), które to sformułowanie prowadzi do maksymalizacji średniego wskaźnika produktywności WYJŚCIE/WEJŚCIE. Średnia produktywność nigdy nie została zaakceptowana w rachunkowości zarządczej (w biznesie) jako kryterium wydajności lub cel, który należy maksymalizować, ponieważ oznaczałoby to koniec dochodowego biznesu. Zamiast tego funkcja produkcji jest formułowana jako funkcja DOCHÓD=F(PRODUKCJA-WEJŚCIE), która ma zostać zmaksymalizowana. Celem gry jest maksymalizacja dochodów, a nie maksymalizacja produktywności czy produkcji.

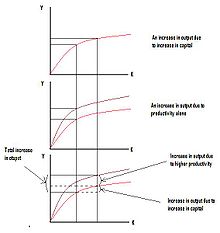
Abstrakcyjny przykład

Dekompozycja wzrostu produkcji na ten spowodowany technologią i ten spowodowany wzrostem kapitału (kliknij, aby powiększyć)

Model rozliczania wzrostu jest zwykle wyrażany w postaci wykładniczej funkcji wzrostu. Jako abstrakcyjny przykład rozważmy gospodarkę, której całkowita produkcja (PKB) rośnie w tempie 3% rocznie. W tym samym okresie jej kapitał rośnie o 6% rocznie, a siła robocza o 1%. Wkład stopy wzrostu kapitału w produkcję jest równy stopie wzrostu ważonej udziałem kapitału w produkcji ogółem, a wkład pracy jest określony przez stopę wzrostu pracy ważoną udziałem pracy w dochodzie. 2/3 1/3 udział kapitału w produkcji wynosi , to wynosi udział pracy (zakładając, że są to jedyne dwa czynniki produkcji). Oznacza to, że część ) 0,027 wzrostu produkcji spowodowana zmianami czynników wynosi 0,06×( czyli 1/3)+0,01×(2/3 . = 2,7% Oznacza to, że nadal istnieje 0,3% wzrostu produkcji, którego nie można wyjaśnić. Ta reszta to wzrost produktywności czynników, który miał miejsce w danym okresie, lub miara postępu technologicznego w tym czasie.

Konkretny przykład

Rachunek wzrostu można również wyrazić w postaci modelu arytmetycznego, który jest tutaj stosowany, ponieważ jest bardziej opisowy i zrozumiały. Zasada modelu księgowego jest prosta. Ważone stopy wzrostu nakładów (czynników produkcji) są odejmowane od ważonych stóp wzrostu produkcji. Ponieważ wynik księgowy uzyskuje się przez odjęcie, często nazywany jest „resztą”. Resztę często definiuje się jako stopę wzrostu produkcji, której nie wyjaśniają ważone udziałami stopy wzrostu nakładów.

Możemy wykorzystać rzeczywiste dane procesowe modelu produkcji , aby pokazać logikę modelu rozliczania wzrostu i zidentyfikować możliwe różnice w stosunku do modelu produktywności. Gdy dane produkcyjne są takie same w porównaniu modeli, różnice w wynikach księgowych wynikają tylko z modeli księgowych. Otrzymujemy następujące rozliczenie wzrostu z danych produkcyjnych.

Kalkulacja modelu rozliczania wzrostu

Procedura rozliczania wzrostu przebiega w następujący sposób. Najpierw obliczane są stopy wzrostu produkcji i nakładów, dzieląc liczby z okresu 2 przez liczby z okresu 1. Następnie wagi nakładów są obliczane jako udziały nakładów w całkowitym nakładzie (okres 1). Ważone szybkości wzrostu (WG) uzyskuje się przez ważenie szybkości wzrostu wagami. Wynik księgowy uzyskuje się przez odjęcie ważonych stóp wzrostu nakładów od stopy wzrostu produkcji globalnej. W tym przypadku wynik księgowy wynosi 0,015, co implikuje wzrost produktywności o 1,5%.

Zauważamy, że model produktywności podaje wzrost wydajności o 1,4% na podstawie tych samych danych produkcyjnych. Różnica (1,4% w stosunku do 1,5%) wynika z różnej wielkości produkcji zastosowanej w modelach. W modelu produktywności wielkość nakładów jest miarą wielkości produkcji, co daje stopę wzrostu 1,063. W tym przypadku produktywność definiowana jest w następujący sposób: wielkość produkcji przypadająca na jednostkę wielkości produkcji. W modelu rozliczania wzrostu wielkość produkcji jest używana jako miara wielkości produkcji, co daje stopę wzrostu 1,078. W tym przypadku produktywność definiowana jest następująco: zużycie nakładów przypadające na jednostkę wielkości produkcji. Przypadek ten można łatwo zweryfikować za pomocą modelu produktywności wykorzystującego wielkość produkcji jako wielkość produkcji.

Wynik księgowy modelu rozliczania wzrostu jest wyrażony jako liczba indeksu, w tym przykładzie 1,015, która przedstawia średnią zmianę produktywności. Jak wykazano powyżej, nie możemy wyciągnąć prawidłowych wniosków na podstawie średnich liczb dotyczących produktywności. Wynika to z faktu, że produktywność jest ujmowana jako zmienna niezależna oddzielona od podmiotu, do którego należy, czyli tworzenia dochodu realnego. Stąd, jeśli porównamy w praktyce dwa wyniki rozliczania wzrostu tego samego procesu produkcyjnego, nie wiemy, który z nich jest lepszy pod względem wydajności produkcji. Musimy znać osobno efekty dochodowe zmiany produktywności i zmiany wielkości produkcji lub ich łączny efekt dochodowy, aby zrozumieć, który wynik jest lepszy io ile lepszy.

Ten rodzaj naukowego błędu o złym poziomie analizy został już dawno rozpoznany i opisany. Wygotski przestrzega przed ryzykiem oddzielenia badanego zagadnienia od całego środowiska, którego istotą jest to zagadnienie. Studiując tylko ten odosobniony problem, prawdopodobnie dojdziemy do błędnych wniosków. Drugi praktyczny przykład ilustruje to ostrzeżenie. Załóżmy, że badamy właściwości wody podczas gaszenia pożaru. Jeśli skupimy się w recenzji na małych elementach całości, w tym przypadku na pierwiastkach tlenu i wodoru, dojdziemy do wniosku, że wodór jest gazem wybuchowym, a tlen jest katalizatorem spalania. Dlatego ich woda złożona może być wybuchowa i nieodpowiednia do gaszenia pożaru. Ten błędny wniosek wynika z faktu, że składniki zostały oddzielone od podmiotu.

Wyprowadzenie techniczne

Całkowita produkcja gospodarki jest modelowana jako wytwarzana przez różne czynniki produkcji, przy czym kapitał i praca są głównymi czynnikami we współczesnych gospodarkach (chociaż można również uwzględnić ziemię i zasoby naturalne). Zwykle jest to wychwytywane przez zagregowaną funkcję produkcji :

${\ Displaystyle Y = F (A, K, L)}$

gdzie Y to całkowita produkcja, K to zasób kapitału w gospodarce, L to siła robocza (lub populacja), a A to czynnik „całkowity” dla technologii, roli instytucji i innych odpowiednich sił, który mierzy, jak produkcyjnie kapitał i praca jest wykorzystywana w produkcji.

Standardowe założenia co do postaci funkcji F(.) są takie, że jest ona rosnąca w K, L, A (jeśli zwiększysz produktywność lub zwiększysz liczbę użytych czynników, otrzymasz więcej produkcji) i że jest jednorodna pierwszego stopnia , lub innymi słowy, że istnieją stałe korzyści skali (co oznacza, że ​​jeśli podwoisz zarówno K, jak i L, uzyskasz podwójny wynik). Założenie stałych korzyści skali ułatwia założenie doskonałej konkurencji , co z kolei oznacza, że ​​czynniki uzyskują swoje produkty krańcowe:

${\ Displaystyle {dY} / {dK} = MPK = r}$

${\ Displaystyle {dY} / {dL} = MPL = w}$

gdzie MPK oznacza dodatkowe jednostki produkcji wytworzonej przy dodatkowej jednostce kapitału i analogicznie dla MPL. Płace wypłacane pracownikom są oznaczane przez w, a stopa zysku lub realna stopa procentowa jest oznaczana przez r. Zauważmy, że założenie doskonałej konkurencji pozwala nam przyjmować ceny zgodnie z danymi. Dla uproszczenia przyjmujemy cenę jednostkową (tj. P = 1), a więc ilości reprezentują również wartości we wszystkich równaniach.

Jeśli całkowicie zróżniczkujemy powyższą funkcję produkcji, otrzymamy;

$dY = F_ {A} dA + F_ {K} dK + F_ {L} dL$

gdzie oznacza pochodną cząstkową względem czynnika i lub w przypadku kapitału i pracy $produktów$ Przy doskonałej konkurencji równanie to wygląda następująco:

$F_ {A} dA + MPKdK + MPLdL = F_ {A$

Jeśli podzielimy przez Y i przeliczymy każdą zmianę na stopy wzrostu, otrzymamy:

${\ Displaystyle {dY}/{Y} = ({F_ {A}} A/{Y}) ({dA}/{A}) + (r {K}/{Y}) * ({dK}/ {K})+(w{L}/{Y})*({dL}/{L})}$

lub oznaczając tempo wzrostu (zmianę procentową w czasie) czynnika jako ${\ Displaystyle g_ {i} = {di}/{i}}$ otrzymujemy:

$\ Displaystyle g_ {Y} = ({F_ {A}} A / {Y})*g_{A}+({rK}/{Y})*g_{K}+({wL}/{Y})*g_{L}}$

Wtedy ${\ Displaystyle {rK} / {Y}} to udział w całkowitym dochodzie$${wL} / {Y}}$ który trafia do kapitału, co można oznaczyć jako i $Displaystyle$ to udział w całkowitym dochodzie przeznaczony na pracę, oznaczony przez ${\ displaystyle 1-\ alpha}$ . To pozwala nam wyrazić powyższe równanie jako:

${\ Displaystyle g_ {Y} = {F_ {A}} A / {Y} * g_ {A} + \alpha *g_{K}+(1-\alpha )*g_{L}}$

$}$ zasadzie wszystkie terminy są obserwowalne i można $je$$zaobserwować$$displaystyle$ K } mierzone przy użyciu standardowych metod księgowania dochodu narodowego (przy czym zasób kapitału jest mierzony przy użyciu stóp inwestycji metodą wieczystej inwentaryzacji ). Termin ${\ displaystyle {\ frac {F_ {A} A} {Y}} * g_ {A}}$ nie jest jednak bezpośrednio obserwowalny, ponieważ oddaje rozwój technologiczny i poprawę produktywności, które nie są związane ze zmianami wykorzystania czynników. Termin ten jest zwykle określany jako rezydualny wzrost produktywności czynników produkcji Solowa lub całkowity wzrost produktywności czynników produkcji. Nieznacznie przestawiając poprzednie równanie, możemy to zmierzyć jako część wzrostu produkcji całkowitej, która nie jest spowodowana (ważonym) wzrostem nakładów czynników produkcji:

${\ Displaystyle SolowResidual = g_ {Y} - \ alfa * g_ {K} - (1 -\alfa )*g_{L}}$

Innym sposobem wyrażenia tej samej idei jest przeliczenie na mieszkańca (lub na pracownika), w którym odejmujemy stopę wzrostu siły roboczej z obu stron:

${\ Displaystyle SolowResidual = g_ {(Y/L)} - \ alfa * g_ {(K. /L)}}$

który stwierdza, że ​​stopa wzrostu technologicznego to ta część stopy wzrostu dochodu na mieszkańca, która nie wynika z (ważonej) stopy wzrostu kapitału na osobę.