Aksjomaty Huzity-Hatoriego

Aksjomaty Huzita-Justin lub aksjomaty Huzita-Hatori to zestaw reguł związanych z matematycznymi zasadami origami , opisującymi operacje, które można wykonać podczas składania kartki papieru. Aksjomaty zakładają, że operacje są wykonywane na płaszczyźnie (tj. idealnej kartce papieru), a wszystkie fałdy są liniowe . To nie jest minimalny zestaw aksjomatów, ale raczej pełny zestaw możliwych pojedynczych fałd.

Pierwsze siedem aksjomatów zostało po raz pierwszy odkrytych przez francuskiego matematyka i foldera Jacquesa Justina w 1986 roku. Aksjomaty od 1 do 6 zostały ponownie odkryte przez japońsko - włoskiego matematyka Humiaki Huzitę i przedstawione na Pierwszej Międzynarodowej Konferencji na temat Origami w Edukacji i Terapii w 1991 roku. Aksjomaty od 1 do 5 zostały ponownie odkryte przez Auckly i Cleveland w 1995. Aksjomat 7 został ponownie odkryty przez Koshiro Hatori w 2001; Robert J. Lang znalazł również aksjomat 7.

Siedem aksjomatów

Pierwsze 6 aksjomatów to aksjomaty Justina lub aksjomaty Huzity. Aksjomat 7 został odkryty przez Jacquesa Justina. Koshiro Hatori i Robert J. Lang również znaleźli aksjomat 7. Aksjomaty są następujące:

1. Biorąc pod uwagę dwa różne punkty p ₁ i p ₂ , istnieje unikalna fałda, która przechodzi przez oba z nich.
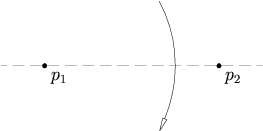
2. Biorąc pod uwagę dwa różne punkty p ₁ i p ₂ , istnieje unikalna fałda , która umieszcza p ₁ na p ₂ .
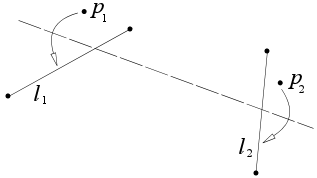
3. Biorąc pod uwagę dwie linie l ₁ i l ₂ , istnieje fałda, która umieszcza l ₁ na l ₂ .
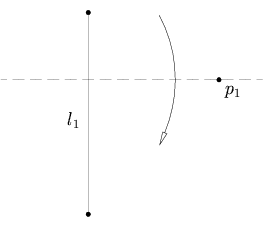
4. Mając dany punkt p ₁ i prostą l ₁ , istnieje unikalne zagięcie prostopadłe do l ₁ , które przechodzi przez punkt p ₁ .
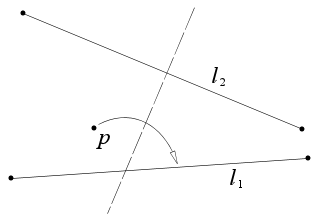
5. Biorąc pod uwagę dwa punkty p ₁ i p ₂ oraz prostą l ₁ , istnieje fałda , która umieszcza p ₁ na l ₁ i przechodzi przez p ₂ .
6. Biorąc pod uwagę dwa punkty p ₁ i p ₂ oraz dwie proste l ₁ i l ₂ , istnieje fałda, która umieszcza p ₁ na l ₁ i p ₂ na l ₂ .
7. Mając jeden punkt p i dwie proste l ₁ i l ₂ , istnieje fałda, która umieszcza p na l ₁ i jest prostopadła do l ₂ .

Aksjomat 5 może mieć 0, 1 lub 2 rozwiązania, podczas gdy Aksjomat 6 może mieć 0, 1, 2 lub 3 rozwiązania. W ten sposób otrzymane geometrie origami są silniejsze niż geometrie kompasu i liniału , gdzie maksymalna liczba rozwiązań aksjomatu wynosi 2. Zatem geometria kompasu i liniału rozwiązuje równania drugiego stopnia, podczas gdy geometria origami lub orygametria może rozwiązywać równania trzeciego stopnia i rozwiązywać problemy, takie jak trysekcja kąta i podwojenie sześcianu . Konstrukcja fałdy gwarantowana przez Aksjomat 6 wymaga „przesunięcia” papieru, czyli neusis , co nie jest dozwolone w klasycznych konstrukcjach kompasu i liniału. Użycie neusis wraz z kompasem i liniałem pozwala na trysekcję dowolnego kąta.

Detale

Aksjomat 1

Biorąc pod uwagę dwa punkty p ₁ i p ₂ , istnieje unikalna fałda, która przechodzi przez oba z nich.

W postaci parametrycznej równanie prostej przechodzącej przez dwa punkty jest następujące:

${\ Displaystyle F (s) = p_ {1} + s (p_ {2} -p_ {1}).}$

Aksjomat 2

Biorąc pod uwagę dwa punkty p ₁ i p ₂ , istnieje unikalna fałda , która umieszcza p ₁ na p ₂ .

Jest to równoważne znalezieniu dwusiecznej prostopadłej odcinka p ₁ p ₂ . Można to zrobić w czterech krokach:

• P. $P (s) = p_$ s p ₁ + p ₁ Displaystyle s
• Znajdź punkt środkowy p _środek P ( s ) _
• Znajdź wektor v ^perp prostopadły do ​​P ( s )
• Równanie parametryczne zagięcia ma wtedy postać:

${\ Displaystyle F (s) = p _ {\ operatorname {środek}} + s \ cdot \ mathbf {v} ^ {\ operatorname {sprawca}}.}$

Aksjomat 3

Biorąc pod uwagę dwie linie l ₁ i l ₂ , istnieje fałda, która umieszcza l ₁ na l ₂ .

Jest to równoważne znalezieniu dwusiecznej kąta między l ₁ a l ₂ . Niech p ₁ i p ₂ będą dowolnymi dwoma punktami na l ₁ i niech q ₁ i q ₂ będą dowolnymi dwoma punktami na l ₂ . Niech u i v będą również jednostkowymi wektorami _kierunkowymi odpowiednio l1 i l2 _; to jest:

${\ Displaystyle \ mathbf {u} = (p_ {2} - p_ {1}) / \ lewo | ( p_ {2} - p_ {1}) \ prawo |}$

${\ Displaystyle \ mathbf {v} = (q_ {2} -q_ {1}) / \ lewo | (q_ {2} -q_ {1}) \ prawo |.}$

Jeśli dwie proste nie są równoległe, to ich punkt przecięcia to:

${\ Displaystyle p _ {\ operatorname {int}} = p_ {1} + s _ {\ operatorname {int}} \ cdot \ mathbf {u}}$

Gdzie

${\ Displaystyle s_ {int} = - {\ Frac {\ mathbf {v} ^ {\ perp} \ cdot (p_ {1} -q_ {1})} {\ mathbf {v} ^ {\ perp} \ cdot \mathbf {u} }}.}$

Kierunek jednej z dwusiecznych wynosi wtedy:

${\ Displaystyle \ mathbf {w} = {\ Frac {\ lewo | \ mathbf {u} \ prawo | \ mathbf {v} + \ lewo | \ mathbf {v} \ prawo | \ mathbf {u}} {\ lewo |\mathbf {u} \right|+\left|\mathbf {v} \right|}}.}$

A parametryczne równanie zagięcia to:

${\ Displaystyle F (s) = p _ {\ operatorname {int}} + s \ cdot \ mathbf {w}.}$

Istnieje również druga dwusieczna, prostopadła do pierwszej i przechodząca przez p _int . Złożenie wzdłuż tej drugiej dwusiecznej również pozwoli uzyskać pożądany rezultat w postaci umieszczenia l ₁ na l ₂ . Wykonanie jednego lub drugiego z tych zagięć może nie być możliwe, w zależności od położenia punktu przecięcia.

Jeśli dwie proste są równoległe, to nie mają punktu przecięcia. Zagięcie musi być linią pośrodku między l ₁ a l ₂ i równoległą do nich.

Aksjomat 4

Mając dany punkt p ₁ i prostą l ₁ , istnieje unikalne zagięcie prostopadłe do l ₁ , które przechodzi przez punkt p ₁ .

Jest to równoważne znalezieniu prostopadłej do l ₁ przechodzącej przez p ₁ . Jeśli znajdziemy jakiś wektor v , który jest prostopadły do ​​prostej l ₁ , to parametryczne równanie zagięcia wygląda następująco:

${\ Displaystyle F (s) = p_ {1} + s \ cdot \ mathbf {v}.}$

Aksjomat 5

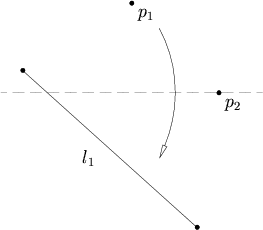
Biorąc pod uwagę dwa punkty p ₁ i p ₂ oraz prostą l ₁ , istnieje fałda , która umieszcza p ₁ na l ₁ i przechodzi przez p ₂ .

Ten aksjomat jest równoważny znalezieniu przecięcia prostej z okręgiem, więc może mieć 0, 1 lub 2 rozwiązania. Linia jest wyznaczona przez l ₁ , a okrąg ma środek w punkcie p ₂ i promień równy odległości od p ₂ do p ₁ . Jeśli prosta nie przecina okręgu, nie ma rozwiązań. Jeśli prosta jest styczna do okręgu, to jest jedno rozwiązanie, a jeśli prosta przecina okrąg w dwóch miejscach, to są dwa rozwiązania.

Jeśli znamy dwa punkty na prostej ( x ₁ , y ₁ ) i ( x ₂ , y ₂ ), to prostą można wyrazić parametrycznie jako:

${\ Displaystyle x = x_ {1} + s (x_ {2} -x_ {1})}$

${\ Displaystyle y = y_ {1} + s (y_ {2} -y_ {1}).}$

Niech okrąg będzie określony przez jego środek w punkcie p ₂ = ( x _c , y _c ), o promieniu ${\ displaystyle r = \ lewo | p_ {1} - p_ {2} \ prawo |}$ . Wtedy okrąg można wyrazić jako:

${\ Displaystyle (xx_ {c}) ^ {2} + (yy_ {c}) ^ {2} = r ^ {2}.}$

Aby wyznaczyć punkty przecięcia prostej z okręgiem, podstawiamy składowe x i y równań dla prostej do równania dla okręgu, otrzymując:

${\ Displaystyle (x_ {1} + s (x_ {2} -x_ {1}) -x_ {c}) ^ {2} + (y_ {1} + s (y_ {2} -y_ {1}) -y_{c})^{2}=r^{2}.}$

Lub uproszczone:

${\ Displaystyle jako ^ {2} + bs + c = 0}$

Gdzie:

${\ Displaystyle a = (x_ {2} -x_ {1}) ^ {2} + (y_ {2} -y_ {1} )^{2}}$

${\ Displaystyle b = 2 (x_ {2} -x_ {1}) (x_ {1} -x_ {c}) + 2 (y_ {2} -y_ {1}) (y_ {1} -y_ {c})}$

${\ Displaystyle c = x_ {c} ^ {2} + y_ {c} ^ {2} + x_ {1} ^ {2} + y_ {1} ^ {2} -2 (x_ {c} x_ {1} }+y_{c}y_{1})-r^{2}.}$

Następnie po prostu rozwiązujemy równanie kwadratowe:

${\ Displaystyle {\ Frac {-b \ pm {\ sqrt {b ^ {2} -4ac}}} {2a}}.}$

Jeśli dyskryminator b ² − 4 ac < 0, nie ma rozwiązań. Okrąg nie przecina ani nie dotyka linii. Jeśli wyróżnik jest równy 0, to istnieje jedno rozwiązanie, w którym prosta jest styczna do okręgu. A jeśli dyskryminator jest większy niż 0, istnieją dwa rozwiązania reprezentujące dwa punkty przecięcia. Nazwijmy rozwiązania d ₁ i d ₂ , jeśli istnieją. Mamy 0, 1 lub 2 segmenty linii:

${\ Displaystyle m_ {1} = {\ overline {p_ {1} d_ {1}}}}$

${\ Displaystyle m_ {2} = {\ overline {p_ {1} d_ {2}}}.}$

Zagięcie F ₁ ( s ) prostopadłe do m ₁ przechodzące przez jego środek spowoduje umieszczenie p ₁ na linii w miejscu d ₁ . Podobnie zagięcie F ₂ ( s ) prostopadłe do m ₂ przechodzące przez jego środek spowoduje umieszczenie p ₁ na linii w miejscu d ₂ . Zastosowanie Aksjomatu 2 z łatwością to umożliwia. Równania parametryczne fałd są zatem następujące:

${\ Displaystyle {\ rozpocząć {wyrównane} F_ {1} (s) & = p_ {1} + {\ Frac {1} {2}} (d_ {1} -p_ {1}) + s (d_ {1} }-p_{1})^{\perp }\\[8pt]F_{2}(s)&=p_{1}+{\frac {1}{2}}(d_{2}-p_{1 })+s(d_{2}-p_{1})^{\perp}.\end{wyrównane}}}$

Aksjomat 6

Biorąc pod uwagę dwa punkty p ₁ i p ₂ oraz dwie proste l ₁ i l ₂ , istnieje fałda, która umieszcza p ₁ na l ₁ i p ₂ na l ₂ .

Ten aksjomat jest równoważny znalezieniu prostej stycznej jednocześnie do dwóch parabol i można go uznać za równoważny rozwiązaniu równania trzeciego stopnia, ponieważ na ogół istnieją trzy rozwiązania. Dwie parabole mają ogniska, _{odpowiednio ,} p1 i p2 , z kierunkami określonymi _{odpowiednio przez} l1 i l2 .

Ta fałda jest nazywana fałdą Belocha na cześć Margharity P. Beloch , która w 1936 roku wykazała za jej pomocą, że origami może być używane do rozwiązywania ogólnych równań sześciennych.

Aksjomat 7

Mając jeden punkt p i dwie linie l ₁ i l ₂ , które nie są równoległe, istnieje fałda, która umieszcza p na l ₁ i jest prostopadła do l ₂ .

Ten aksjomat został pierwotnie odkryty przez Jacquesa Justina w 1989 roku, ale został przeoczony i ponownie odkryty przez Koshiro Hatori w 2002 roku. Robert J. Lang udowodnił, że ta lista aksjomatów uzupełnia aksjomaty origami.

Konstruowalność

Podzbiory aksjomatów można wykorzystać do konstruowania różnych zestawów liczb. Pierwsze trzy mogą być użyte z trzema podanymi punktami nie na linii, aby zrobić to, co Alperin nazywa konstrukcjami Thaliańskimi.

Pierwsze cztery aksjomaty z dwoma danymi punktami definiują system słabszy niż konstrukcje kompasu i liniału : każdy kształt, który można złożyć za pomocą tych aksjomatów, można zbudować za pomocą kompasu i liniału, ale niektóre rzeczy można skonstruować za pomocą kompasu i liniału, których nie można złożyć za pomocą te aksjomaty. Liczby, które można skonstruować, nazywane są liczbami origami lub pitagorejskimi, jeśli odległość między dwoma podanymi punktami wynosi 1, to wszystkie konstruowalne punkty mają postać gdzie ( α $Displaystyle (\ alfa, \ beta)}$${\ displaystyle \ alpha}$$liczbami$ są Pitagorasa. $Liczby pitagorejskie$$.$ zawierające liczby wymierne i ilekroć jest taką

Dodanie piątego aksjomatu daje liczby euklidesowe , czyli punkty konstruowalne za pomocą kompasu i linii prostej .

Dodając neusis aksjomat 6, można wykonać wszystkie konstrukcje kompasowo-liniowe i nie tylko. W szczególności konstruowalne wielokąty foremne $}$ tymi aksjomatami to wielokąty z bokami, gdzie jest ${\ Displaystyle 2 ^ {a} 3 ^ {b} \ rho \ geq 3$ iloczyn różnych liczb pierwszych Pierponta . Konstrukcje z prostą linią kompasową dopuszczają tylko te z $\ geq 3}$ boki, gdzie jest $liczb$ różnych pierwszych Fermata . (Liczby pierwsze Fermata są podzbiorem liczb pierwszych Pierponta).

Siódmy aksjomat nie pozwala na konstruowanie kolejnych aksjomatów. Siedem aksjomatów daje wszystkie pojedyncze konstrukcje, które można wykonać, zamiast być minimalnym zestawem aksjomatów.

Ósmy aksjomat

Istnienie ósmego aksjomatu stwierdził Lucero w 2017 r., co można wyrazić następująco: wzdłuż danej linii l _{1 zachodzi fałda} . Nowy aksjomat został znaleziony po wyliczeniu wszystkich możliwych przypadków między konstruowalnymi punktami i prostymi na płaszczyźnie. Chociaż nie tworzy nowej linii, jest jednak potrzebny w rzeczywistym składaniu papieru, gdy wymagane jest złożenie warstwy papieru wzdłuż linii zaznaczonej na warstwie bezpośrednio poniżej.

Linki zewnętrzne

• Konstrukcje geometryczne origami autorstwa Thomasa Hulla
• Matematyczna teoria konstrukcji origami i liczb autorstwa Rogera C. Alperina
• Lang, Robert J. (2003). „Konstrukcje origami i geometryczne” (PDF) . Roberta J. Langa . Źródło 2007-04-12 . {{ cite journal }} : Cite journal wymaga |journal= ( pomoc )