Składanie mapy
W matematyce składania papieru , składania mapy i składania znaczków to dwa problemy związane z liczeniem, na ile sposobów można złożyć kartkę papieru. W problemie składania znaczków papier jest paskiem znaczków z fałdami między nimi, a fałdy muszą leżeć na fałdach. W problemie składania mapy papier jest mapą podzieloną załamaniami na prostokąty, a zagięcia muszą ponownie leżeć tylko wzdłuż tych zagięć.
Lucas (1891) przypisuje wynalezienie problemu składania znaczków Émile'owi Lemoine'owi . Touchard (1950) dostarcza kilku innych wczesnych odniesień.
Oznaczone znaczki
W problemie składania znaczków papier do złożenia to pasek kwadratowych lub prostokątnych znaczków oddzielonych zagięciami, a znaczki można złożyć tylko wzdłuż tych zagięć. W jednej powszechnie rozważanej wersji problemu uważa się, że każdy znaczek można odróżnić od siebie, więc dwa zagięcia paska znaczków są uważane za równoważne tylko wtedy, gdy mają ten sam pionowy ciąg znaczków. Na przykład istnieje sześć sposobów na złożenie paska trzech różnych znaczków:
Obejmują one wszystkie sześć permutacji znaczków, ale w przypadku więcej niż trzech znaczków nie wszystkie permutacje są możliwe. Jeśli dla permutacji p istnieją dwie liczby i oraz j o takiej samej parzystości , że cztery liczby i , j , i + 1 oraz j + 1 pojawiają się w p w tym porządku cyklicznym , to p nie może zostać zwinięte. Warunek parzystości oznacza, że fałdy między stemplami i i i + 1 , a między znaczkami j i j + 1 pojawiają się po tej samej stronie stosu złożonych znaczków, ale warunek cyklicznej kolejności implikuje, że te dwa zagięcia krzyżują się, co jest fizyczną niemożliwością. Na przykład czteroelementowa permutacja 1324 nie może zostać złożona, ponieważ ma zakazany wzór z i = 1 i j = 3 . Wszystkie pozostałe permutacje, bez tego wzoru, można złożyć. Liczba różnych sposobów złożenia paska n znaczków jest określona przez ciąg
- 1, 2, 6, 16, 50, 144, 462, 1392, 4536, 14060, 46310, 146376, 485914, 1557892, 5202690, ... (sekwencja A000136 w OEIS ) .
Liczby te są zawsze podzielne przez n (ponieważ cykliczna permutacja składanej sekwencji znaczków jest zawsze składana), a ilorazy tego podziału to
- 1, 1, 2, 4, 10, 24, 66, 174, 504, 1406, 4210, 12198, 37378, 111278, 346846, 1053874, ... (sekwencja A000682 w OEIS ) ,
liczba różnych topologicznie sposobów, w jakie półnieskończona krzywa może wykonać n przecięć z linią, zwanych „półmeandrami”.
Czy istnieje formuła lub algorytm czasu wielomianowego do liczenia rozwiązań problemu składania znaczków?
W latach 60. John E. Koehler i WF Lunnon wdrożyli algorytmy , które w tamtym czasie mogły obliczyć te liczby dla maksymalnie 28 znaczków. Pomimo dodatkowych badań znane metody obliczania tych liczb wymagają wykładniczego czasu jako funkcji n . Zatem nie jest znany żaden wzór ani skuteczny algorytm, który mógłby rozszerzyć tę sekwencję do bardzo dużych wartości n . Niemniej jednak heurystyczne z fizyki mogą być wykorzystane do przewidywania tempa wykładniczego wzrostu tej sekwencji.
Problem składania stempla zwykle uwzględnia tylko liczbę możliwych stanów złożenia paska znaczków, bez rozważania, czy jest możliwe fizyczne zbudowanie złożenia przez sekwencję ruchów rozpoczynających się od rozłożonego paska znaczków. Jednak zgodnie z rozwiązaniem problemu reguły stolarza każdy stan złożony można skonstruować (lub równoważnie można go rozłożyć).
Nieopisane znaczki
W innej odmianie problemu składania stempla pasek znaczków jest uważany za pusty, tak że nie można odróżnić jednego jego końca od drugiego, a dwa zagięcia są uważane za odrębne tylko wtedy, gdy mają różne kształty. Odwrócenie złożonego paska do góry nogami lub tyłem do przodu nie jest uważane za zmianę jego kształtu, więc trzy znaczki mają tylko dwa zagięcia, krzywą w kształcie litery S i spiralę. Mówiąc bardziej ogólnie, liczba fałd z tą definicją to
- 1, 1, 2, 5, 14, 38, 120, 353, 1148, 3527, 11622, 36627, 121622, 389560, 1301140, 4215748, ... (sekwencja A001011 w OEIS )
Mapy
Składanie mapy polega na tym, na ile sposobów można złożyć prostokątną mapę wzdłuż jej zagięć, aby każde zagięcie utworzyło fałdę górską lub dolinową. Różni się od składania znaczków tym, że zawiera zarówno pionowe, jak i poziome zagięcia, a nie tylko zagięcia w jednym kierunku.
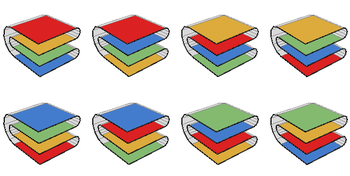
Istnieje osiem sposobów składania mapy 2 × 2 wzdłuż jej zagięć, licząc każdą inną pionową sekwencję złożonych kwadratów jako odrębny sposób składania mapy:
Jednak ogólny problem liczenia liczby sposobów złożenia mapy pozostaje nierozwiązany. Liczba sposobów składania n × n jest znana tylko dla n ≤ 7 . Oni są:
Złożoność
Biorąc pod uwagę przypisanie górskiej doliny dla zagięć mapy, czy można skutecznie przetestować, czy można ją złożyć na płasko?
Problemy składania mapy i składania znaczków są związane z problemem w matematyce origami , czy kwadrat ze wzorem zagięć można złożyć do płaskiej figury. Jeśli kierunek składania ( fałd górski lub fałd doliny ) jest przypisany do każdego zagięcia paska znaczków, można sprawdzić, czy wynik można złożyć płasko w czasie wielomianowym .
W przypadku tego samego problemu na mapie (podzielonej na prostokąty fałdami z przypisanymi kierunkami) nie wiadomo, czy ogólnie istnieje wielomianowy algorytm składania w czasie, chociaż algorytm wielomianowy jest znany dla map 2 × n . W ograniczonym przypadku, w którym mapa ma być złożona przez sekwencję „prostych” fałd, które składają papier wzdłuż jednej linii, problem jest wielomianowy. Niektóre rozszerzenia problemu, na przykład do nieprostokątnych arkuszy papieru, są NP-zupełne .
Nawet w przypadku jednowymiarowego paska znaczków, z jego fałdami już oznaczonymi jako fałdy górskie lub dolinowe, NP-trudno jest znaleźć sposób na złożenie go, który zminimalizowałby maksymalną liczbę znaczków leżących między dwoma stemplami dowolnego zagięcia.
Zobacz też
- Regularna sekwencja składania papieru , nieskończona sekwencja zer i jedynek opisująca jeden ze sposobów składania pasków znaczków
Linki zewnętrzne
- Eric W. Weisstein , Składanie map ( składanie znaczków ) w MathWorld .
- „Składanie paska oznaczonych znaczków” z projektu The Wolfram Demonstrations Project: http://demonstrations.wolfram.com/FoldingAStripOfLabeledStamps/