Regularna sekwencja składania papieru

W matematyce regularna sekwencja składania papieru , znana również jako sekwencja krzywej smoka , jest nieskończoną sekwencją zer i jedynek. Otrzymuje się go z powtarzającej się częściowej sekwencji

1, ?, 0, ?, 1, ?, 0, ?, 1, ?, 0, ?, ...

wypełniając znaki zapytania inną kopią całej sekwencji. Kilka pierwszych wyrazów wynikowej sekwencji to:

1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, ... (sekwencja A014577 w OEIS )

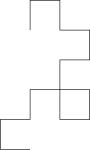
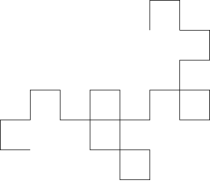
Jeśli pasek papieru jest składany wielokrotnie na pół w tym samym kierunku, $prawo$ , otrzyma $,$ lewo lub w jest określony przez wzór zer i jedynek w pierwszym ${\ Displaystyle 2 ^ {i} -1}$ terminy regularnej sekwencji składania papieru. Otwarcie każdego zagięcia w celu utworzenia narożnika pod kątem prostym (lub, równoważnie, wykonanie sekwencji skrętów w lewo i w prawo przez regularną siatkę, zgodnie ze wzorem sekwencji składania papieru) tworzy sekwencję wielokątnych łańcuchów, które zbliżają się do fraktala krzywej smoka :

1	1 1 0	1 1 0 1 1 0 0	1 1 0 1 1 0 0 1 1 1 0 0 1 0 0	...

Nieruchomości

Wartość dowolnego danego terminu $,$$sekwencji$ składania papieru, zaczynając od znaleźć rekurencyjnie w następujący Podziel ${\ displaystyle n}$ przez dwa, tyle razy, ile to możliwe, aby uzyskać rozkład na czynniki postaci gdzie ${\ Displaystyle n = m \ cdot 2 ^ {k}}$ gdzie ${\ displaystyle m}$ jest liczbą nieparzystą . Następnie

$${\ Displaystyle t_ {n} = {\ rozpocząć {przypadki} 1 i {\ tekst {jeśli}} m \ równoważnik 1 \ mod 4 \\ 0 i { \text{if }}m\równoważnik 3\mod 4\end{przypadki}}}$$

Tak więc, na przykład, ${\ displaystyle t_ {12} = t_ {3} = 0}$ : dwukrotne podzielenie 12 przez dwa daje liczbę nieparzystą 3. Jako inny przykład, ${\ displaystyle t_{13}=1}$ , ponieważ 13 jest zgodne z 1 mod 4.

Słowo składania papieru 1101100111001001..., które jest tworzone przez połączenie warunków regularnej sekwencji składania papieru, jest stałym punktem reguł morfizmu lub podstawiania ciągów

11 → 1101

01 → 1001

00 → 10

1000 → 1100

następująco:

11 → 1101 → 11011001 → 1101100111001001 → 11011001110010011101100011001001 ...

Z reguł morfizmu można zauważyć, że słowo składające się na papier zawiera co najwyżej trzy kolejne zera i co najwyżej trzy kolejne jedynki.

Sekwencja składania papieru spełnia również relację symetrii:

${\ Displaystyle t_ {n} = {\ rozpocząć {przypadki} 1 i {\ tekst {jeśli}} n =2^{k}\\1-t_{2^{k}-n}&{\text{if }}2^{k-1}<n<2^{k}\end{przypadki}}}$

co pokazuje, że słowo składania papieru można skonstruować jako granicę innego iterowanego procesu w następujący sposób:

1

1 1 0

110 1 100

1101100 1 1100100

110110011100100 1 110110001100100

W każdej iteracji tego procesu na końcu łańcucha poprzedniej iteracji umieszczana jest cyfra 1, a następnie ciąg ten jest powtarzany w odwrotnej kolejności, zastępując 0 przez 1 i odwrotnie.

Funkcja generująca

Funkcja generująca sekwencji składania papieru jest dana przez

${\ Displaystyle G (t_ {n}; x) = \ suma _ {n = 1} ^ {\ infty} t_ {n} x ^ {n} \,.}$

Z konstrukcji sekwencji składania papieru widać, że G spełnia zależność funkcyjną

${\ Displaystyle G (t_ {n}; x) = G (t_ {n}; x ^ {2}) + \ suma _ {n = 0} ^ {\ infty} x ^ {4n + 1} = G ( t_{n};x^{2})+{\frac {x}{1-x^{4}}}\,.}$

Stała składania papieru

0 Podstawienie x = 0,5 do funkcji generującej daje liczbę rzeczywistą między a 1 , której rozwinięciem binarnym jest słowo składania papieru

${\ Displaystyle G (t_ {n}; {\ Frac {1} {2}}) = \ suma _ {n = 1} ^ { \infty}{\frac {t_{n}}{2^{n}}}}$

Ta liczba jest znana jako stała składania papieru i ma wartość

${\ Displaystyle \ suma _ {k = 0} ^ {\ infty} {\ Frac {8 ^ {2 ^ {k}}}} 2^{2^{k+2}}-1}}=0,85073618820186...}$ (sekwencja A143347 w OEIS )

Ogólna kolejność składania papieru

Regularna sekwencja składania papieru odpowiada składaniu paska papieru konsekwentnie w tym samym kierunku. Jeśli pozwolimy, aby kierunek fałdy zmieniał się na każdym kroku, otrzymamy bardziej ogólną klasę sekwencji. Mając sekwencję binarną ( _fi ) _, możemy zdefiniować ogólną sekwencję składania papieru z instrukcjami składania ( fi ).

Dla słowa binarnego w , niech w ^‡ oznacza odwrotność dopełnienia w . Zdefiniuj operatora F _a jako

${\ Displaystyle F_ {a}: w \ mapsto waw ^ {\ ddagger} \}$

₀ a następnie zdefiniuj ciąg słów w zależności od ( f _i ) przez w = ε,

${\ Displaystyle w_ {n} = F_ {f_ {1}} (F_ {f_ {2}} (\ cdots F_ {f_ {n}} (\ varepsilon) \ cdots)} \ .}$

Granicą w sekwencji w _n jest sekwencja składania papieru. Regularna sekwencja składania papieru odpowiada sekwencji składania f _i = 1 dla wszystkich i .

Jeśli n = m ·2 ^k gdzie m jest nieparzyste, to wtedy

${\ Displaystyle t_ {n} = {\ rozpocząć {przypadki} f_ {j} i {\ tekst {jeśli}} m \ równoważny 1\mod 4\\1-f_{j}&{\tekst{jeśli}}m\równoważny 3\mod 4\end{przypadki}}}$

które mogą być użyte jako definicja sekwencji składania papieru.

Nieruchomości

• Sekwencja składania papieru nie jest ostatecznie okresowa.
• Sekwencja składania papieru jest 2- automatyczna wtedy i tylko wtedy, gdy sekwencja składania jest ostatecznie okresowa (1-automatyczna).

•    Allouche, Jean-Paul; Szallit, Jeffrey (2003). Sekwencje automatyczne: teoria, zastosowania, uogólnienia . Wydawnictwo Uniwersytetu Cambridge . ISBN 978-0-521-82332-6 . Zbl 1086.11015 .