Historia hindusko-arabskiego systemu liczbowego
| Część serii o |
| systemach liczbowych |
|---|
| Lista systemów liczbowych |
System liczb hindusko-arabskich to dziesiętny system liczbowy z wartością miejsca , który wykorzystuje glif zerowy , jak w „205”.
Jego glify pochodzą od indyjskich cyfr Brahmi . Pełny system pojawił się między VIII a IX wiekiem i po raz pierwszy został opisany poza Indiami w dziele Al-Khwarizmi On the Calculation with Hindu Liczby (ok. 825), a następnie w czterotomowej pracy Al-Kindi On the Use of cyfry indyjskie (ok. 830). Obecnie zwykle używa się nazwy cyfry hindusko-arabskie .
System dziesiętny
Historycy śledzą współczesne cyfry w większości języków na podstawie cyfr Brahmi , które były używane około połowy III wieku pne. System wartości miejsca rozwinął się jednak później. Cyfry Brahmi znaleziono w inskrypcjach w jaskiniach i na monetach w regionach w pobliżu Pune, Maharashtra i Uttar Pradesh w Indiach. Cyfry te (z niewielkimi zmianami) były używane do IV wieku.
W okresie Gupta (początek IV wieku do końca VI wieku) cyfry Gupta rozwinęły się z cyfr Brahmi i zostały rozrzucone na dużych obszarach przez imperium Guptów, gdy podbijały one terytorium. Począwszy od około VII wieku, cyfry Gupta rozwinęły się w cyfry Nagari.
Rozwój w Indiach
W okresie wedyjskim (1500-500 pne), motywowany geometryczną konstrukcją ołtarzy przeciwpożarowych i astronomią, stosowaniem systemu numerycznego i podstawowych operacji matematycznych rozwinęło się w północnych Indiach. Kosmologia hinduska wymagała opanowania bardzo dużych liczb, takich jak kalpa (czas życia wszechświata), o której mówi się, że wynosi 4 320 000 000 lat, a „orbita nieba” to 18 712 069 200 000 000 yojanów . Liczby zostały wyrażone za pomocą „nazwanego zapisu wartości miejsca”, używając nazw dla potęg 10, takich jak dasa , shatha , sahasra , ayuta , niyuta , prayuta , arbuda , nyarbuda , samudra , madhya , anta , parardha itd., ostatnia z nich jest nazwą biliona (10 12 ). Na przykład liczba 26 432 została wyrażona jako „2 ayuta , 6 sahasra , 4 shatha , 3 dasa , 2”. W tekście buddyjskim Lalitavistara Mówi się, że Budda przekazał schemat liczb do 10 53 .
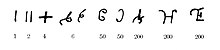
Forma cyfr w inskrypcjach Aśoki zapisanych pismem Brahmi (połowa III wieku p.n.e.) obejmowała osobne znaki dla liczb od 1 do 9, od 10 do 90, 100 i 1000. Wielokrotność 100 lub 1000 była reprezentowana przez modyfikację (lub „szyfrowanie”) znaku liczby przy użyciu znaku liczby mnożnika. Takie zaszyfrowane cyfry bezpośrednio reprezentowały nazwane cyfry wartości miejsc używane werbalnie. Nadal były używane w inskrypcjach do końca IX wieku.
W swoim przełomowym tekście z 499 roku n.e. Aryabhata opracował nowatorski system liczb pozycyjnych, używając sanskryckich spółgłosek dla małych liczb i samogłosek dla potęg 10. Korzystając z tego systemu, liczby do miliarda można było wyrazić za pomocą krótkich fraz, np. np. khyu-ghṛ reprezentujące liczbę 4 320 000. System nie przyjął się, ponieważ generował całkiem trudne do wymówienia wyrażenia, ale mógł przekazać zasadę pozycyjnego systemu liczbowego (nazywanego dasa-gunottara , wykładniki 10) późniejszym matematykom. Bardziej eleganckie katapayadi schemat został opracowany w późniejszych stuleciach, reprezentujący system wartości miejsc obejmujący zero.
Cyfry miejscowe bez zera

Podczas gdy cyfry w tekstach i inskrypcjach wykorzystywały nazwaną notację wartości miejsca, w obliczeniach mógł być zastosowany bardziej wydajny zapis, prawdopodobnie z I wieku n.e. Obliczenia przeprowadzono na glinianych tabliczkach pokrytych cienką warstwą piasku, co dało początek terminowi dhuli-karana („praca z piasku”) dla wyższych obliczeń. Karl Menninger uważa, że w takich obliczeniach musieli zrezygnować z zaszyfrowanych cyfr i zapisać tylko sekwencje cyfr reprezentujących liczby. Zero byłoby reprezentowane jako „brakujące miejsce”, takie jak kropka. Pojedynczy rękopis z dostępnymi nam przykładami prac, The Rękopis Bakhshali (o niejasnej dacie) wykorzystuje system wartości miejsca z kropką oznaczającą zero. Kropka była nazywana shunya-sthana „pustym miejscem”. Ten sam symbol był również używany w wyrażeniach algebraicznych dla nieznanego (jak w kanonicznym x we współczesnej algebrze).
Tekstowe odniesienia do systemu wartości miejsc pojawiają się od V wieku n.e. Buddyjski filozof Vasubandhu w V wieku mówi, że „kiedy [ten sam] gliniany element liczący znajduje się w miejscu jednostek, oznacza się go jako jeden, gdy w setkach, sto”. W komentarzu do Jogasutr Patańdżalego z V wieku czytamy: „Tak jak linia w miejscu setek [oznacza] sto, w miejscu dziesiątek dziesięć, a jedna w miejscu jedności, tak jedna i ta sama kobieta jest nazywana matka, córka i siostra”.
System zwany bhūta-sankhya („liczby obiektów” lub „konkretne liczby”) został zastosowany do przedstawiania cyfr w wersetach sanskryckich, używając pojęcia reprezentującego cyfrę jako samej cyfry. Tekst Jain zatytułowany Lokavibhaga , datowany na 458 rok n.e., wspomina o zobiektywizowanej liczbie
" panchabhyah khalu shunyebhyah param dve sapta chambaram ekam trini cha rupam cha "
co oznacza „pięć pustek, potem dwa i siedem, niebo, jeden i trzy oraz formę”, tj. liczbę 13107200000. Takie zobiektywizowane liczby były szeroko stosowane od VI wieku, zwłaszcza po Varāhamihira ( ok. 575 n.e. ) . Zero jest wyraźnie reprezentowane w takich liczbach, jak „pustka” ( sunya ) lub „niebo-przestrzeń” ( ambara akaśa ). Odpowiednio, kropka użyta zamiast zera w pisanych cyfrach była określana jako sunya-bindu .
Cyfry miejscowe z zerem

W 628 roku n.e. astronom-matematyk Brahmagupta napisał swój tekst Brahma Sphuta Siddhanta , który zawierał pierwsze matematyczne podejście do zera. Zdefiniował zero jako wynik odejmowania liczby od samej siebie, postulował liczby ujemne i omawiał ich właściwości w ramach działań arytmetycznych. Jego słowem oznaczającym zero było shunya (pustka), tym samym terminem używanym wcześniej dla pustego miejsca w 9-cyfrowym systemie wartości miejsca. Dało to nowe spojrzenie na shunya-bindu jako cyfra i utorowała drogę do ostatecznej ewolucji cyfry zerowej. Kropka była nadal używana przez co najmniej 100 lat później i została przeniesiona do Azji Południowo-Wschodniej i Arabii. Pismo Sharada Kaszmiru zachowało kropkę jako zero do dziś.
Pod koniec VII wieku liczby dziesiętne zaczęły pojawiać się w inskrypcjach w Azji Południowo-Wschodniej, a także w Indiach. Niektórzy uczeni utrzymują, że pojawiły się one jeszcze wcześniej. Często cytowany jest grant z miedzianej płyty z Mankani z VI wieku, noszący cyfrę 346 (odpowiadającą 594 n.e.). Ale jego niezawodność jest przedmiotem sporu. Pierwsze niekwestionowane wystąpienie 0 w inskrypcji ma miejsce w Gwalior w 876 roku n.e., zawierające cyfrę „270” w notacji zaskakująco podobnej do naszej. W VIII i IX wieku używano zarówno starych cyfr Brahmi, jak i nowych cyfr dziesiętnych, czasami pojawiających się w tych samych inskrypcjach. W niektórych dokumentach widać, że przejście nastąpiło około 866 roku n.e.
Adopcja przez Arabów
Przed powstaniem kalifatu hindusko -arabski system liczbowy przemieszczał się już na zachód i został wspomniany w Syrii w 662 r. przez syryjskiego nestoriańskiego uczonego Severusa Sebokhta , który napisał, co następuje:
- „Pominę wszelkie dyskusje na temat nauki Indian…, ich subtelnych odkryć w astronomii, odkryć bardziej pomysłowych niż te dokonane przez Greków i Babilończyków, oraz ich cennych metod obliczeniowych, których nie da się opisać. powiedzieć, że to obliczenie odbywa się za pomocą dziewięciu znaków. Gdyby ci, którzy wierzą, ponieważ mówią po grecku, że dotarli do granic nauki, czytali teksty indyjskie, byliby przekonani, nawet jeśli trochę późno dzień, że są inni, którzy wiedzą coś wartościowego”.
Według Historii uczonych ludzi Al-Qifti :
- „… osoba z Indii przedstawiła się kalifowi al-Mansurowi w roku [776 ne], który był dobrze zaznajomiony z siddhantą metodą obliczeń związanych z ruchem ciał niebieskich i posiadał sposoby obliczania równań oparte na półakord [zasadniczo sinus] obliczony w pół stopniach… Wszystko to jest zawarte w pracy… z której, jak twierdził, wziął półakord obliczony na jedną minutę. Al-Mansur nakazał przetłumaczenie tej książki na arabski i praca do napisania, oparta na tłumaczeniu, aby dać Arabom solidną podstawę do obliczania ruchów planet…”
Dziełem tym najprawdopodobniej była Brāhmasphuṭasiddhānta (Otwarcie wszechświata) Brahmagupty, napisana w 628 roku. Niezależnie od tego, czy jest to błędne, ponieważ wszystkie teksty indyjskie po Aryabhatiya Aryabhaty używały indyjskiego systemu liczbowego, z pewnością z tego W tym czasie Arabowie mieli tłumaczenie tekstu zapisanego w indyjskim systemie liczbowym.
W swoim tekście The Arithmetic of Al-Uqlîdisî (Dordrecht: D. Reidel, 1978) badania AS Saidana nie były w stanie w pełni odpowiedzieć, w jaki sposób cyfry dotarły do świata arabskiego:
- „Wydaje się prawdopodobne, że dryfował stopniowo, prawdopodobnie przed VII wiekiem, przez dwa kanały, jeden zaczynający się od Sind, przechodzący perską filtrację i rozprzestrzeniający się na obszarze znanym obecnie jako Bliski Wschód, a drugi wychodzący z wybrzeży Oceanu Indyjskiego i rozciągające się na południowe wybrzeża Morza Śródziemnego”.
Al-Uqlidisi opracował notację do reprezentowania ułamków dziesiętnych. Cyfry zyskały sławę dzięki ich zastosowaniu w kluczowym dziele perskiego matematyka Al -Khwarizmiego , którego książka „ O obliczeniach z liczbami hinduskimi” została napisana około 825 roku, oraz arabskiego matematyka Al-Kindiego , który napisał cztery tomy (zob. ]) „O użyciu liczb indyjskich” (Ketab fi Isti'mal al-'Adad al-Hindi) około 830 r. Między innymi przyczyniły się one do rozpowszechnienia indyjskiego systemu numeracji na Bliskim Wschodzie i Zachód.
Rozwój symboli
Rozwój cyfr we wczesnej Europie pokazano poniżej:
Liczydło a hindusko-arabski system liczbowy na wczesnych nowożytnych obrazach
Adopcja w Europie
- 976 . Pierwsze cyfry arabskie w Europie pojawiły się w Codex Vigilanus w roku 976.
- 1202 . Fibonacci , włoski matematyk, który studiował w Béjaïa (Bougie) w Algierii, promował system liczb arabskich w Europie swoją książką Liber Abaci , opublikowaną w 1202 roku.
- 1482 . System nie wszedł jednak do powszechnego użytku w Europie, aż do wynalezienia druku . (Zobacz na przykład mapę świata Ptolemeusza z 1482 r. Wydrukowaną przez Lienharta Holle'a w Ulm i inne przykłady w Muzeum Gutenberga w Moguncji w Niemczech ).
- 1512 . Liczby pojawiają się w ich współczesnej formie na stronie tytułowej „Conpusicion de la arte de la arismetica y juntamente de geometría” napisanej przez Juana de Ortegę.
- 1549 . To jest poprawny format i kolejność „ nowoczesnych liczb ” na stronie tytułowej Libro Intitulado Arithmetica Practica autorstwa Juana de Yciar , baskijskiego kaligrafa i matematyka, Saragossa 1549.
W ciągu ostatnich kilku stuleci europejska odmiana cyfr arabskich rozpowszechniła się na całym świecie i stopniowo stała się najczęściej używanym systemem liczbowym na świecie.
Nawet w wielu krajach w językach, które mają własne systemy liczbowe, europejskie cyfry arabskie są szeroko stosowane w handlu i matematyce .
Wpływ na arytmetykę
Znaczenie rozwoju systemu liczb pozycyjnych opisuje francuski matematyk Pierre-Simon Laplace (1749–1827), który napisał:
To Indie dały nam pomysłową metodę wyrażania wszystkich liczb za pomocą dziesięciu symboli, z których każdy otrzymuje wartość pozycji, jak również wartość bezwzględną; głęboka i ważna idea, która wydaje się nam teraz tak prosta, że ignorujemy jej prawdziwą wartość, ale sama jej prostota, wielka łatwość, jakiej udzieliła wszystkim obliczeniom, stawia naszą arytmetykę na pierwszym miejscu użytecznych wynalazków i docenimy ją wielkość tego osiągnięcia, gdy przypomnimy sobie, że umknęło ono geniuszowi Archimedesa i Apoloniusza , dwóch największych umysłów stworzonych przez starożytność.
Zobacz też
- Lista tematów systemu liczbowego
- Lista systemów liczbowych
- Tabela symboli matematycznych według daty wprowadzenia
Notatki
- ^ „Cyfry hindusko-arabskie” . Zarchiwizowane od oryginału w dniu 2005-12-27 . Źródło 2005-12-13 .
- ^ ab " "Abu Yusuf Yaqub ibn Ishaq al-Sabbah Al-Kindi . Zarchiwizowane od oryginału w dniu 2007-10-26 . Źródło 2007-01-12 .
- ^ a b c John J O'Connor i Edmund F. Robertson (listopad 2000). „cyfry indyjskie” . Archiwum historii matematyki MacTutor . Zarchiwizowane od oryginału w dniu 2015-07-06 . Źródło 2022-07-24 .
- ^ Smith i Karpiński 2013 , s. 12–15.
- Bibliografia _ _ 2.
- ^ Plofker 2009 , s. 68–69.
- Bibliografia _ _ 14.
- Bibliografia _ _ 397.
- ^ Smith i Karpiński 2013 , s. 15.
- Bibliografia _ _ 57.
- Bibliografia _ _ 395.
- Bibliografia _ _ 44.
- ^ Plofker 2009 , s. 73–75.
- ^ Plofker 2009 , s. 75–77.
- Bibliografia _ _ 398.
- ^ Sarasvati i Jyotishmati 1979 , s. 27, 66.
- Bibliografia _ _ 46.
- Bibliografia _ _ 417.
- Bibliografia _ _ 416.
- ^ Twierdzono, że tekst Yavana-jataka z połowy III wieku n.e. (o „horoskopie greckim”) wykorzystywał urządzenie bhūta-sankhyas ( Plofker 2009 , s. 47). Ale obecnie uważa się to za błąd w interpretacji. ( Mak, Bill M. (2013), „The Transmission of Greek Astral Science into India Reconsidered-Critical Uwagi on the Content and the Newly Discovered Manuscript of the Yavanajātaka”, History of Science in South Asia , 1 : 1–20, doi : 10.18732/H2RP4T )
- ^ Smith & Karpiński 2013 , Ch. III; Ifrah 1998 , s. 411–418; Menninger 2013 , s. 398
- ^ abcd , Oxford indyjska Salomon, Richard (1998), Epigrafia : przewodnik po badaniu inskrypcji w sanskrycie, prakrycie i innych językach indo-aryjskich University Press, USA, s. 61–63, ISBN 978- 0-19-535666-3
- ^ Smith, David Eugeniusz; Karpiński, Ludwik Karol (1911). Cyfry hindusko-arabskie . Boston, Londyn, Ginn and Company. P. 52.
- ^ Dla nowoczesnego obrazu
- Bibliografia _ _ 439.
- Bibliografia _ _ 45.
- ^ Shastri, Ajaya Mitra (1998), „Mankaṇi Charter of Taralasvāmin and the Antiquity of the Decimal Notation”, Annals of the Bhandarkar Oriental Research Institute , 79 (1/4): 161–170, JSTOR 41694535
- ^ Plofker 2009 , s. 45–46; Menninger 2013 , s. 396–397; Ifrah 1998 , s. 400
-
^ a b c d
„cyfry arabskie” . MacTutor Archiwum Historii Matematyki . Źródło 2021-05-23 .
{{ cite web }}: CS1 maint: stan adresu URL ( link ) - ^ Ifrah, Georges (2000). Uniwersalna historia liczb: od prehistorii do wynalezienia komputera . Dawid Bellos. Nowy Jork: Wiley. ISBN 0-471-37568-3 . OCLC 42291138 .
- ^ Biografia Al-Uqlidisi autorstwa JJ O'Connora i EF Robertsona
- ^ Najwcześniejsze zastosowania symboli ułamków autorstwa Jeffa Millera
- ^ „Conpusicion de la arte de la arismetica y juntamente de geometría” napisany przez Juana de Ortegę
- ^ Kumar Raj (2003). Eseje o starożytnych Indiach . Wydawnictwo Discovery. s. 196–. ISBN 978-81-7141-682-0 .
- Źródła
- Ifrah, Georges (1998) [po raz pierwszy opublikowana w języku francuskim w 1981 r.], The Universal History of Numbers: From Prehistory to the Invention of the Computer , Harvill, ISBN 978-1-860-46324-2
- Menninger, Karl (2013) [opublikowane po raz pierwszy przez MIT Press w 1969 r.], Number Words and Number Symbols: A Cultural History of Numbers , przetłumaczone przez Paula Broneera, Courier Corporation, ISBN 978-0-486-31977-3
- Plofker, Kim (2009), Matematyka w Indiach , Princeton University Press, ISBN 978-0-691-12067-6
- Sarasvati, Svami Satya Prakash; Jyotishmati, Usha (1979), The Bakhshali Manuscript: An Ancient Treatise of Indian Arithmetic (PDF) , Allahabad: Dr. Ratna Kumari Svadhyaya Sansthan, zarchiwizowane z oryginału (PDF) w dniu 2014-06-20 , pobrane 2016-01-19
- Smith, Niemcy ; Karpinski, LC (2013) [po raz pierwszy opublikowano w Bostonie, 1911], The Hindu-Arabic Liczby , Dover, ISBN 978-0486155111
- „Rozwój arytmetyki hindusko-arabskiej i tradycyjnej chińskiej” profesora Lam Lay Yong, członka Międzynarodowej Akademii Historii Nauki
- Cyfry indyjskie autorstwa JJ O'Connora i EF Robertsona
- Cyfry arabskie autorstwa JJ O'Connora i EF Robertsona
- Cyfry hindusko-arabskie
- System liczb arabskich autorstwa: JJ O'Connor i EF Robertson Zarchiwizowane 2010-02-23 w Wayback Machine
- Filliozat, Pierre-Sylvain (2004), „Starożytna matematyka sanskrycka: tradycja ustna i literatura pisana”, w: Chemla, Karine ; Cohen, Robert S.; Renn, Jürgen; i in. (red.), History of Science, History of Text (Boston Series in the Philosophy of Science) , Dordrecht: Springer Holandia, 254 strony, s. 137–157, doi : 10.1007/1-4020-2321-9_7 , ISBN 978 -1-4020-2320-0 .











