system katapajadi
| Część serii o |
| systemach liczbowych |
|---|
| Lista systemów liczbowych |
) of numerical notation is an Indian to numeralsnumbers System Kaṭapayadi ( Devanagari : कटपयादि, znany również jako Paralppēru , malajalam : പരൽപ്പേര് ) notacji <a i=8>numerycznej starożytny indyjski <a i=10>alfasylabowy system liczbowy przedstawiający litery na <a i=14><a i=15>cyfry łatwego zapamiętania <a i=17>liczb słów lub <a i=20><a i=21>wersetów or verses . Przypisując więcej niż jedną literę do jednej cyfry i unieważniając niektóre inne litery jako bezwartościowe, system ten zapewnia elastyczność w tworzeniu znaczących słów z liczb, które można łatwo zapamiętać.
Historia
Najstarsze dostępne dowody na użycie systemu Katapayadi (sanskryt: कटपयादि) pochodzą z Grahacāraṇibandhana autorstwa Haridatta w 683 roku n.e. Użyto go w Laghu·bhāskarīya·vivaraṇa napisanej przez Śankarę narayaṇę w 869 roku n.e.
Niektórzy twierdzą, że system pochodzi od Vararuci . W niektórych tekstach astronomicznych popularnych w Kerali pozycje planet były zakodowane w systemie Katapayadi. Za pierwsze takie dzieło uważa się Chandra-vakyani z Vararuci , którego tradycyjnie przypisuje się IV wiek n.e. Dlatego gdzieś na początku pierwszego tysiąclecia można racjonalnie oszacować pochodzenie systemu Katapayadi .
Aryabhata w swoim traktacie Ārya·bhaṭīya używał podobnego, bardziej złożonego systemu do przedstawiania liczb astronomicznych . Nie ma ostatecznych dowodów na to, czy Ka-ṭa-pa-yā-di wywodzi się z numeracji Āryabhaṭa .
Geograficzny zasięg użytkowania
Prawie wszystkie dowody na użycie systemu Ka-ṭa-pa-yā-di pochodzą z południowych Indii , zwłaszcza z Kerali . Niewiele wiadomo o jego zastosowaniu w północnych Indiach. Jednak na sanskryckim astrolabium odkrytym w północnych Indiach stopnie wysokości są zaznaczone w systemie Katapayadi . Jest przechowywany w Bibliotece Sarasvati Bhavan Uniwersytetu Sampurnanand Sanskrit w Varanasi .
System Ka-ṭa-pa-yā-di nie ogranicza się do Indii. W Birmie odkryto kilka palijskich chronogramów opartych na systemie Ka-ṭa-pa-yā-di .
Zasady i praktyki
Poniższy werset znaleziony w Sadratnamala Śankarawarmana wyjaśnia mechanizm systemu.
नञावचश्च शून्यानि संख्या: कटपयादय:। मिश्रे तूपान्त्यहल् संख्या न च चिन्त्यो हलस् वर: ॥
Transliteracja:
nanyāvacaśca śūnyāni saṃkhyāḥ katapayadayaḥ miśre tupantyahal saṃkhyā na ca cintyo halasvaraḥ
Tłumaczenie: na (न), ña (ञ) i a (अ)-s, tj. samogłoski reprezentują zero . Dziewięć liczb całkowitych jest reprezentowanych przez grupę spółgłosek zaczynającą się od ka , ṭa , pa , ya . W koniunkcji spółgłoskowej liczy się tylko ostatnia ze spółgłosek. Spółgłoskę bez samogłoski należy zignorować.
Wyjaśnienie: Przypisanie liter do cyfr jest zgodne z następującym układem (odpowiednio w skryptach dewanagari, kannada, telugu i malajalam)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| ka क ಕ క ക | kha ख ಖ ఖ ഖ | ga ग ಗ గ ഗ | gha घ ಘ ఘ ഘ |
nga ङ ಙ ఙ ങ |
ca च ಚ చ ച | cha छ ಛ ఛ ഛ | ja ज ಜ జ ജ | jha झ ಝ ఝ ഝ | nya ञ ಞ ఞ ഞ |
| Ta ट ಟ ట ട | Tha ठ ಠ ఠ ഠ | Da ड ಡ డ ഡ | ḍha ढ ಢ ఢ ഢ | ṇa ण ಣ ణ ണ | ta त ತ త ത | tak थ ಥ థ ഥ | da द ದ ద ദ | dha ध ಧ ధ ധ | na न ನ న ന |
| pa प ಪ ప പ | pha फ ಫ ఫ ഫ | ba ब బ ബ | bha भ ಭ భ ഭ | ma म ಮ మ മ | – | – | – | – | – |
| tak य ಯ య യ | ra र ರ ర ര | la ल ల ల ല | va व ವ వ വ | śa श ಶ శ ശ | Sa ष ಷ ష ഷ | sa स ಸ స സ | ha ह ಹ హ ഹ | – | – |
- Spółgłoski mają przypisane cyfry zgodnie z powyższą tabelą. Na przykład ba (ब) to zawsze 3, podczas gdy 5 może być reprezentowane przez nga (ङ) lub ṇa (ण) lub ma (म) lub śha (श).
- Wszystkie samodzielne samogłoski, takie jak a (अ) i ṛ (ऋ), są przypisane do zera.
- W przypadku koniunkcji spółgłoski dołączone do niesamogłoski będą bezwartościowe. Na przykład kya (क्य) jest utworzone przez k (क्) + y (य्) + a (अ). Jedyną spółgłoską stojącą z samogłoską jest ya (य). Zatem odpowiednią cyfrą dla kya (क्य) będzie 1.
- W systemie nie ma możliwości reprezentacji separatora dziesiętnego .
- Indianie używali do numerowania systemu cyfr hindusko-arabskich , tradycyjnie zapisywanych rosnącymi wartościami miejsc od lewej do prawej. Jest to zgodne z regułą „अङ्कानां वामतो गतिः”, co oznacza, że liczby idą od prawej do lewej.
Wariacje
- Spółgłoska ḷ (malajalam: ള, Devanāgarī: ळ, kannada: ಳ) jest używana w pracach wykorzystujących system Kaṭapayadi, podobnie jak tabela sinusów Madhawy .
- Praktycy późnego średniowiecza nie odwzorowują samodzielnych samogłosek na zero. Ale czasami jest uważany za bezwartościowy.
Stosowanie
Matematyka i astronomia
- Tablica sinusów Mādhavy skonstruowana przez XIV-wiecznego matematyka z Kerali - astronoma Mādhavę z Saṅgama · grama wykorzystuje system Katapayadi do zapisania sinusów trygonometrycznych kątów.
- Karaṇa·paddhati , napisana w XV wieku, ma następującą ślokę dla wartości pi (π)
- അനൂനനൂന്നാനനനുന്നനിത്യൈ-
- സ്സമാഹതാശ്ചക്രകല ാവിഭക്താഃ
- <a i=3>ചണ്ഡാംശുചന്ദ്രാധമകുംഭിപാലൈർ-
- വ്യാസസ്തദര്ദ്ധം ത്രിഭമൗര്വിക സ്യാത്
- Transliteracja
- anūnanūnnānananunnnanityai
- ssmāhatāścakra kalāvibhaktoḥ
- caṇḍāṃśucandrādhamakuṃbhipālair
vyāsastadarddhaṃ tribhamaurvika syāt
- Daje obwód koła o średnicy, anūnanūnnānanananunnanityai (10 000 000 000) jako caṇḍāṃśucandrādhamakuṃbhipālair (31415926536).
- Sad·ratna·māla Śankary Varmana używa systemu Katapayadi. Pierwszy werset rozdziału 4 Sad·ratna·mālā kończy się wersem:
- (स्याद्) भद्राम्बुधिसिद्धजन्मगणितश ्रद्धा स्म यद् भूपगी:
- Transliteracja
- (syād) bhadrāmbudhisiddhajanmagaṇitaśraddhā sma yad bhūpagīḥ
- Rozdzielenie spółgłosek w odpowiedniej frazie daje,
| भ bha | द् d | रा Ra | म् m | बु bu | द् d | धि dhi | सि si | द् d | ध dha | ja | न् przym | म ma | ग ga | णि ṇi | त ta | श् ś | र ra | द् d | धा dha | स् s | म ma | tak | द् d | भू bhu | प pa | गी gī |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | – | 2 | – | 3 | – | 9 | 7 | – | 9 | 8 | – | 5 | 3 | 5 | 6 | – | 2 | – | 9 | – | 5 | 1 | – | 4 | 1 | 3 |
- Odwracając cyfry do współczesnego użycia malejącego porządku miejsc dziesiętnych, otrzymujemy 314159265358979324 , co jest wartością pi (π) do 17 miejsc po przecinku, z wyjątkiem ostatniej cyfry, która może być zaokrąglona do 4.
- Ten werset szyfruje wartość pi (π) do 31 miejsc po przecinku.
गोपीभाग्यमधुव्रात-शृङ्गिशोदधिसन्धिग॥ खलजीवितखाताव गलहालारसंधर॥
|| ಖಲಜೀವಿತಖಾತಾವ ಗಲಹಾಲಾರಸಂಧರ ||
Ten werset bezpośrednio daje dziesiętny odpowiednik liczby pi podzielonej przez 10: pi/10 = 0,31415926535897932384626433832792
| ఖలజీవితఖాతావ గలహాలారసంధర ||
Tradycyjnie kolejność cyfr jest odwracana, aby utworzyć liczbę, w systemie katapayadi. W tej śloce ta zasada jest łamana.
Muzyka karnatyczna
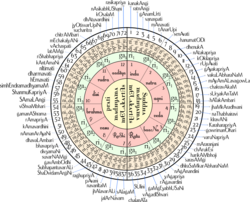
- Melakarta ragas muzyki karnatyckiej jest nazwana w taki sposób , że pierwsze dwie sylaby nazwy podają jej numer. Ten system jest czasami nazywany Ka-ta-pa-ya-di sankhya. Swary „ Pa” są ustalone, a oto jak uzyskać inne swary z numeru melakarta.
- Melakartas od 1 do 36 mają Ma1, a te od 37 do 72 mają Ma2.
- Pozostałe nuty uzyskuje się przez zanotowanie (części całkowitej) ilorazu i reszty, gdy jeden mniejszy niż liczba melakarta jest dzielony przez 6. Jeśli liczba melakarta jest większa niż 36, przed wykonaniem tego kroku odejmij 36 od liczby melakarta.
- Pozycje „Ri” i „Ga”: raga będzie miała:
- Ri1 i Ga1 , jeśli iloraz wynosi 0
- Ri1 i Ga2 , jeśli iloraz wynosi 1
- Ri1 i Ga3 , jeśli iloraz wynosi 2
- Ri2 i Ga2 , jeśli iloraz wynosi 3
- Ri2 i Ga3 , jeśli iloraz wynosi 4
- Ri3 i Ga3 , jeśli iloraz wynosi 5
- Pozycje „Da” i „Ni”: raga będzie miała:
- Da1 i Ni1 , jeśli reszta wynosi 0
- Da1 i Ni2 , jeśli reszta wynosi 1
- Da1 i Ni3 , jeśli reszta wynosi 2
- Da2 i Ni2 , jeśli reszta wynosi 3
- Da2 i Ni3 , jeśli reszta wynosi 4
- Da3 i Ni3 , jeśli reszta wynosi 5
- Zobacz swary w muzyce karnatyckiej, aby uzyskać szczegółowe informacje na temat powyższej notacji.
Raga Dheerasankarabharanam
Schemat katapayadi łączy dha i ra , stąd numer melakarta ragi to 29 (92 odwrócone). 29 mniej niż 36, stąd Dheerasankarabharanam ma Ma1. Podziel 28 (1 mniej niż 29) przez 6, iloraz to 4, a reszta to 4. Dlatego ta raga ma Ri2, Ga3 (iloraz to 4) i Da2, Ni3 (reszta to 4). Dlatego skala tej ragi to Sa Ri2 Ga3 Ma1 Pa Da2 Ni3 SA .
Raga MechaKalyani
Ze schematu kodowania Ma 5, Cha 6. Stąd numer melakarta ragi to 65 (56 odwrócony). 65 jest większe niż 36. Więc MechaKalyani ma Ma2. Ponieważ liczba ragi jest większa niż 36, odejmij od niej 36. 65–36 = 29. 28 (1 mniej niż 29) podzielone przez 6: iloraz=4, reszta=4. Występuje Ri2 Ga3. Występuje Da2 Ni3. Więc MechaKalyani ma notatki Sa Ri2 Ga3 Ma2 Pa Da2 Ni3 SA .
Wyjątek dla Simhendramadhyamam
Zgodnie z powyższym obliczeniem powinniśmy otrzymać Sa 7, Ha 8, podając liczbę 87 zamiast 57 dla Simhendramadhyamam. Idealnie powinno to być Sa 7, Ma 5, podając liczbę 57. Uważa się więc, że imię powinno być zapisane jako Sihmendramadhyamam (jak w przypadku Bra hmana w Sanskryt).
Reprezentacja dat
Ważne daty pamiętano, przeliczając je za pomocą systemu Katapayadi . Daty te są ogólnie przedstawiane jako liczba dni od początku Kali Yugi . Czasami nazywa się to kalidina sankhya .
- CE Kalendarz malajalam znany jako kollavarsham (malajalam: കൊല്ലവർഷം) został przyjęty w Kerali począwszy od 825 roku n.e., <a i=5><a i=6>przebudowując Data ta jest pamiętana jako āchārya vāgbhadā , przeliczona przy użyciu Katapayadi na 1434160 dni od początku Kali Yugi .
- Narayaniyam , napisany przez Melpathura Narayana Bhattathiri , kończy się wersem āyurārogyasaukhyam (ആയുരാരോഗ്യസൌഖ്യം), co oznacza długie życie, zdrowie i szczęście.
| W malajalam | ആയുരാരോഗ്യസൌഖ്യം |
|---|---|
| w dewanagari | आयुरारोग्यसौख्यम् |
| w IAST | āyurarogyasaukhyam |
| Wartość zgodnie z Katapayadi | 1712210 |
- Ta liczba to czas, w którym praca została zakończona, reprezentowana jako liczba dni od początku Kali Yugi , zgodnie z kalendarzem malajalam .
Inni
- Niektórzy ludzie używają systemu Katapayadi do nadawania imion noworodkom.
- Poniższy werset skompilowany w języku malajalam przez Koduṅṅallura Kuññikkuṭṭan Taṃpurān przy użyciu Katapayadi to liczba dni w miesiącach kalendarza gregoriańskiego .
- പുലർന്നാലോ
- കലക്കിലാം <a i=1>ഇല്ല ാ
- ഇല്ലാ പാലെന്നു ഗോപാലന് – ആംഗ്ലമാസദിനം ക്രമാല്
- palahāre pālu <a i=3>nallū
- palahāre pālu nallū, pularnnālo kalakkilāṃ
- gopālan – āṃgḷamāsadinaṃ kramāl Tłumaczenie: Mleko jest najlepsze na śniadanie, rano należy je zamieszać.
- Ale Gopālan mówi, że nie ma mleka – liczba dni w angielskich miesiącach w kolejności.
- Konwersja par liter za pomocą Kaṭapayadi daje - pala (പല) to 31, hāre (ഹാരേ) to 28, pālu പാലു = 31, nallū (ന്നാലോ) is 30, kala (ഇല്ലാ) is 30, (പാലെ) is 31, (നല്ലൂ) to 30, pular (പുലർ) to 31, nnālo ( <a i=4>ന്നാലോ <a i=5>കല ) to 31, kkilāṃ ക്കിലാം) to 31, illā ( <a i=10>ഇല്ലാ ( <a i=12>പാലെ idź (ന്നു ഗോ) wynosi 30, palan (പാലൻ) wynosi 31.
Zobacz też
Dalsza lektura
- AA Hattangadi, Explorations in Mathematics, Universities Press (Indie) Pvt. Ltd., Hyderabad (2001) ISBN 81-7371-387-1 [3]

