Kategoria trójkątna

W matematyce kategoria triangulowana to kategoria z dodatkową strukturą „funktora translacji” i klasą „trójkątów dokładnych”. Wybitnymi przykładami są kategoria pochodna kategorii abelowej , jak również kategoria stabilnej homotopii . Dokładne trójkąty uogólniają krótkie dokładne sekwencje w kategorii abelowej, a także sekwencje włókien i sekwencje włókien kowłóknistych w topologii.

Znaczna część algebry homologicznej jest wyjaśniona i rozszerzona przez język kategorii triangulowanych, czego ważnym przykładem jest teoria kohomologii snopów . W latach sześćdziesiątych typowym zastosowaniem kategorii triangulowanych było rozszerzenie właściwości snopów na przestrzeni X na kompleksy snopów, postrzeganych jako obiekty pochodnej kategorii snopów na X . Niedawno kategorie triangulowane stały się przedmiotami zainteresowania same w sobie. Udowodniono lub przypuszczono wiele równoważności między triangulowanymi kategoriami o różnym pochodzeniu. Na przykład homologicznej symetrii lustrzanej przewiduje, że pochodna kategoria rozmaitości Calabiego – Yau jest równoważna kategorii Fukayi jej „lustrzanej” rozmaitości symplektycznej .

Historia

Kategorie triangulowane zostały wprowadzone niezależnie przez Dietera Puppe (1962) i Jean-Louisa Verdiera (1963), chociaż aksjomaty Puppe'a były mniej kompletne (brak aksjomatu oktaedrycznego (TR 4)). Puppe był motywowany stabilną kategorią homotopii. Kluczowym przykładem Verdiera była kategoria pochodna kategorii abelowej, którą również zdefiniował, rozwijając idee Aleksandra Grothendiecka . Wczesne zastosowania kategorii pochodnych obejmowały dwoistość koherentną i dwoistość Verdiera , która rozszerza dwoistość Poincarégo na przestrzenie osobliwe.

Definicja

Funktor przesunięcia lub translacji na kategorii D jest addytywnym automorfizmem (lub dla niektórych autorów autorównoważnością ) $D$ do D . Często pisze się dla liczb całkowitych n ${\ Displaystyle X [n] = \ Sigma ^ {n} X}$ .

Trójkąt ( X , Y , Z , u , v , w ) składa się z trzech obiektów X , Y i Z wraz z morfizmami $Displaystyle u \ okrężnica X \ do Y}$ \ , ${\ Displaystyle v \ dwukropek Y \ do Z}$ i ${\ Displaystyle w \ dwukropek Z \ do X [1]}$ . Trójkąty są generalnie zapisywane w postaci rozplątanej:

${\ Displaystyle X {\ xrightarrow {{} \ na szczycie u}} Y {\ xrightarrow {{} \ na szczycie v}} Z {\ xrightarrow {{} \ na szczycie w}}X[1],}$

Lub

${\ Displaystyle X {\ xrightarrow {{} \ na szczycie u}} Y {\ xrightarrow {{} \ na szczycie v}} Z {\ xrightarrow {{} \ na szczycie w}}}$

w skrócie.

Kategoria triangulowana to kategoria addytywna D z funktorem translacji i klasą trójkątów, zwanych trójkątami dokładnymi (lub trójkątami wyróżnionymi ), spełniająca następujące właściwości (TR 1), (TR 2), (TR 3) i (TR 4) . (Te aksjomaty nie są całkowicie niezależne, ponieważ (TR 3) można wyprowadzić z innych.)

TR 1

• Dla każdego obiektu X następujący trójkąt jest dokładny:

${\ Displaystyle X {\ overset {\ tekst {id}} {\ do}} X \ do 0 \ do X [1] }$

• Dla każdego morfizmu $kowłóknem$ Z ( zwany lub morfizmu u ) Y trójkąta

${\ Displaystyle X {\ xrightarrow {{} \ na szczycie u}} Y \ do Z \ do X [1]}$

Nazwa „stożek” pochodzi od stożka mapy kompleksów łańcuchowych , który w turn został zainspirowany stożkiem mapującym w topologii. Z innych aksjomatów wynika $, że ​​​​dokładny$ szczególności obiekt Z ) jest określony aż do izomorfizmu przez morfizm , chociaż zawsze aż do unikalnego izomorfizmu.

• Każdy trójkąt izomorficzny z trójkątem dokładnym jest dokładny. Oznacza to, że jeśli

${\ Displaystyle X {\ xrightarrow {{} \ na szczycie u}} Y {\ xrightarrow {{} \ na szczycie v}} Z {\ xrightarrow {{ } \ na szczycie w}} X [1]}$

jest dokładnym trójkątem i ${\ Displaystyle f \ dwukropek X \ do X '}$ , ${\ Displaystyle g \ dwukropek Y \ do Y'}$ , i ${\ Displaystyle h \ dwukropek Z \ do Z '}$ są izomorfizmami, a następnie

${\ Displaystyle X '{\ xrightarrow {guf ^ {-1}}} Y' {\ xrightarrow {hvg ^ {-1}}} Z '{\ xrightarrow {f [1] wh ^ {-1}}} X '[1]}$

jest również dokładnym trójkątem.

TR 2

Jeśli

${\ Displaystyle X {\ xrightarrow {{} \ na szczycie u}} Y {\ xrightarrow {{} \ na szczycie v}} Z {\ xrightarrow {{} \ na szczycie w }}X[1]}$

jest dokładnym trójkątem, to takie są dwa obrócone trójkąty

${\ Displaystyle Y {\ xrightarrow {{} \ na szczycie v}} Z {\ xrightarrow {{} \ na szczycie w}} X [1 ]{\xrightarrow {-u[1]}}Y[1]}$

I

${\ Displaystyle Z [-1] {\ xrightarrow {-w [-1]}} X {\ xrightarrow {{} \ na szczycie u}} Y {\ xrightarrow {{} \ na szczycie v}} Z. \}$

Ze względu na ostatni trójkąt obiekt Z [-1] nazywany jest włóknem morfizmu X $\ Displaystyle X \ do Y}$ .

Drugi obrócony trójkąt ma bardziej złożoną postać, gdy i ${\ Displaystyle$$[-1]} nie$ jedynie wzajemnie odwrotnymi równoważnościami kategorii, ponieważ ${\ Displaystyle -w [-1]}$ jest morfizmem od ${\ Displaystyle Z [-1]}$ do ${\ Displaystyle (X [1]) [-1]}$ i aby uzyskać morfizm do ${\ Displaystyle [X]}$ trzeba komponować z naturalną transformacją ${\ Displaystyle (X [1]) [-1] {\ xrightarrow {}} X}$ . Prowadzi to do złożonych pytań o możliwe które należy nałożyć na naturalne przekształcenia, dokonując i $]}$ na parę odwrotnych $. Ze$$względu na$ problem założenie, że są wzajemnie odwrotnymi izomorfizmami $,$ w definicji kategorii

TR 3

Mając dwa dokładne trójkąty i mapę między pierwszymi morfizmami w każdym trójkącie, istnieje morfizm między trzecimi obiektami w każdym z dwóch trójkątów, który powoduje, że wszystko jest dojeżdżane . Oznacza to, że na poniższym diagramie (gdzie dwa wiersze są dokładnymi trójkątami, a f i g są morfizmami takimi, że gu = u′f ), istnieje mapa h (niekoniecznie unikalna), która powoduje, że wszystkie kwadraty dojeżdżają do pracy:

TR 4: Aksjomat oktaedryczny

Niech ${\ Displaystyle u \ okrężnica X \ do Y}$ i ${\ Displaystyle v \ okrężnica Y \ do Z}$ będą morfizmami i rozważmy złożony morfizm ${\ styl wyświetlania vu\dwukropek X\do Z}$ . Utwórz dokładne trójkąty dla każdego z tych trzech morfizmów zgodnie z TR 1. Aksjomat oktaedryczny stwierdza (w przybliżeniu), że trzy stożki odwzorowania można przekształcić w wierzchołki dokładnego trójkąta, tak że „wszystko dojeżdża”.

Bardziej formalnie, biorąc pod uwagę dokładne trójkąty

${\ Displaystyle X {\ xrightarrow {u \}} Y {\ xrightarrow {j}} Z '{\ xrightarrow {k}} X [1]}$

${\ Displaystyle Y {\ xrightarrow {v \}} Z {\ xrightarrow {l}} X '{\ xrightarrow {i}} Y [1]}$

${\ Displaystyle X {\ xrightarrow {{} \ na szczycie vu}} Z {\ xrightarrow {m}} Y '{\ xrightarrow {n}} X [1]$ }

istnieje dokładny trójkąt

${\ Displaystyle Z '{\ xrightarrow {f}} Y '{\ xrightarrow {g}} X' {\ xrightarrow {h}} Z '[ 1]}$

takie że

${\ Displaystyle l = gm, \ quad k = nf, \ quad h = j [1] i, \ quad ig = u [1] n, \ quad fj = mv.}$

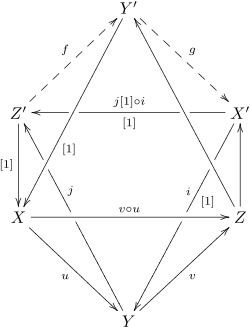
Ten aksjomat nazywa się „aksjomatem ośmiościennym”, ponieważ narysowanie wszystkich obiektów i morfizmów daje szkielet ośmiościanu , którego cztery ściany są dokładnymi trójkątami. Prezentacja tutaj jest autorstwa Verdiera i pojawia się wraz z diagramem ośmiościennym w (Hartshorne 1966 ). Na poniższym diagramie u i v są podanymi morfizmami, a pierwsze litery to stożki różnych map (wybrane tak, aby każdy dokładny trójkąt miał X , a Y i Z list). Różne strzałki zostały oznaczone [1], aby wskazać, że mają „stopień 1”; np. mapa od Z ′ do X jest w rzeczywistości od Z ′ do X [1]. Aksjomat oktaedryczny potwierdza następnie istnienie map f i g tworzących dokładny trójkąt, tak że f i g tworzą trójkąty przemienne na innych ścianach, które je zawierają:

Dwa różne obrazy pojawiają się w (Beilinson, Bernstein & Deligne 1982 ) (Gelfand i Manin ( 2006 ) również przedstawiają pierwszy). Pierwsza przedstawia górną i dolną piramidę powyższego ośmiościanu i stwierdza, że ​​mając dolną piramidę, można wypełnić górną piramidę tak, że dwie ścieżki od Y do Y ′ i od Y ′ do Y , są sobie równe (warunek ten jest pominięty, być może błędnie, w prezentacji Hartshorne'a). Trójkąty oznaczone + są przemienne, a te oznaczone „d” są dokładne:

Drugi schemat to bardziej innowacyjna prezentacja. Dokładne trójkąty są przedstawione liniowo, a diagram podkreśla fakt, że cztery trójkąty w „ośmiościanie” są połączone serią map trójkątów, gdzie trzy trójkąty (czyli te dopełniające morfizmy od X do Y , od Y do Z , i od X do Z ) są podane i twierdzi się istnienie czwartego. Jeden przechodzi między dwoma pierwszymi, „obracając się” wokół X , do trzeciego, obracając się wokół Z , a do czwartego, obracając się wokół X ′. Wszystkie obudowy na tym schemacie są przemienne (zarówno trygony, jak i kwadrat), ale drugi kwadrat przemienny, wyrażający równość dwóch ścieżek od Y ′ do Y , nie jest oczywisty. Wszystkie strzałki skierowane „poza krawędź” mają stopień 1:

Ten ostatni diagram ilustruje również przydatną intuicyjną interpretację aksjomatu oktaedrycznego. W kategoriach triangulowanych trójkąty odgrywają rolę dokładnych sekwencji, dlatego sugestywne jest myślenie o tych obiektach jako o „ilorazach”, ${\ Displaystyle Z'= Y/X}$ i ${\ Displaystyle Y '= Z/X}$ . W tych kategoriach istnienie ostatniego trójkąta wyraża się z jednej strony

${\ Displaystyle X'= Z/Y \}$ (patrząc na trójkąt ${\ Displaystyle Y \ do Z \ do X'\ do}$ ) i

${\ Displaystyle X '= Y'/Z'}$ (patrząc na trójkąt ${\ Displaystyle Z'\ do Y'\ do X'\ do}$ ).

Łącząc to razem, ośmiościenny aksjomat potwierdza „trzecie twierdzenie o izomorfizmie”:

${\ Displaystyle (Z / X) / (Y / X) \ cong Z / Y.}$

Jeśli kategoria triangulowana jest kategorią pochodną D ( A ) kategorii abelowej A , a X , Y , Z są obiektami A postrzeganymi jako kompleksy skoncentrowane w stopniu 0, a mapy ${\ Displaystyle X \ do Y}$ i ${\ Displaystyle Y \ do Z}$ są monomorfizmami w A , to stożki tych morfizmów w D ( A ) są w rzeczywistości izomorficzne z powyższymi ilorazami w A .

Wreszcie Neeman ( 2001 ) formułuje aksjomat oktaedryczny za pomocą dwuwymiarowego diagramu przemiennego z 4 rzędami i 4 kolumnami. Beilinson, Bernstein i Deligne ( 1982 ) również podają uogólnienia ośmiościennego aksjomatu.

Nieruchomości

Oto kilka prostych konsekwencji aksjomatów dla triangulowanej kategorii D .

• Biorąc pod uwagę dokładny trójkąt

${\ Displaystyle X {\ xrightarrow {{} \ na szczycie u}} Y {\ xrightarrow {{} \ na szczycie v}} Z {\ xrightarrow {{{} } \atop w}}X[1]}$

w D , złożenie dowolnych dwóch kolejnych morfizmów wynosi zero. Oznacza to, że vu = 0, wv = 0, u [1] w = 0 i tak dalej.

• Biorąc pod uwagę morfizm ${\ Displaystyle u \ dwukropek X \ do Y}$ , TR 1 gwarantuje istnienie stożka Z dopełniającego dokładnie trójkąt. Dowolne dwa stożki u są izomorficzne, ale izomorfizm nie zawsze jest jednoznacznie określony.

• Każdy monomorfizm w D jest włączeniem sumy bezpośredniej, $}$ każdy epimorfizm jest projekcją $Y$$Displaystyle X \ oplus$ . Powiązanym punktem jest to, że nie należy mówić o „iniekcji” lub „suriektywności” dla morfizmów w kategorii triangulowanej. Każdy morfizm $, który nie$ izomorfizmem, ma niezerowy „kokernel” Z oznacza, że ​​​​istnieje dokładny trójkąt ${\ Displaystyle X \ do Y \to Z\to X[1]}$ ), a także niezerowe „jądro”, mianowicie Z [−1].

Niefunkcjonalność konstrukcji stożka

Jedną z komplikacji technicznych związanych z kategoriami triangulowanymi jest fakt, że konstrukcja stożka nie jest funkcjonalna. Na przykład, biorąc pod uwagę pierścień $i$ mapę wyróżnionych trójkątów

${\ Displaystyle {\ rozpocząć {macierz} R & \ do & 0 & \ do & R [+1] i \ do \\\ strzałka w dół &&\strzałka w dół &&&\\0&\do &R[+1]&\do &R[+1]&\do \end{macierzy}}}$

w ${\ Displaystyle D ^ {b} (R)}$ istnieją dwie mapy, które uzupełniają ten diagram. Może to być mapa tożsamości lub mapa zerowa

${\ Displaystyle {\ rozpocząć {wyrównane} {\ tekst {id}}: & R [+1] \ do R [+1]\\0:&R[+1]\do R[+1]\end{wyrównane}}}$

z których oba są przemienne. Fakt istnienia dwóch map jest cieniem faktu, że kategoria triangulowana jest narzędziem, które koduje granice homotopii i colimit . Jedno rozwiązanie tego problemu zostało zaproponowane przez Grothendiecka , w którym rozważana jest nie tylko kategoria pochodna, ale także kategoria pochodna diagramów tej kategorii. Taki obiekt nazywamy Derivatorem .

Przykłady

1. Przestrzenie wektorowe nad ciałem k tworzą elementarną kategorię triangulowaną, w której X [1] = X dla wszystkich X . Dokładny trójkąt to sekwencja k - liniowych map (zapisywanie tej samej mapy $do Z \ do X \ do$$Displaystyle$ dwa razy), co jest dokładne w X , Y i Z. _
2. Jeśli A jest kategorią addytywną (na przykład kategorią abelową), zdefiniuj $kategorię$ homotopii aby mieć jako obiekty łańcuchowe w A jako morfizmy klasy homotopii morfizmów kompleksy. Wtedy ${\ Displaystyle K (A)}$ jest kategorią triangulowaną. Przesunięcie X [1] to zespół X przesunięty o jeden krok w lewo (i z różniczkami pomnożonymi przez −1). Dokładny trójkąt w $)}$$X$ trójkątem, który jest izomorficzny z trójkątem $[1]}$$\ Displaystyle X$$X$ związany z jakąś mapą kompleksów łańcuchowych (Tu ${\ Displaystyle {\ tekst {stożek}} (f)}$ oznacza stożek odwzorowania mapy łańcucha.)
3. Kategoria pochodna D ( A ) kategorii abelowej A jest kategorią triangulowaną. Skonstruowana jest z kategorii kompleksów C ( A ) przez lokalizowanie względem wszystkich quasi-izomorfizmów . Oznacza to, że formalnie dołącz odwrotny morfizm dla każdego quasi-izomorfizmu. Przedmioty D ( A ) pozostają niezmienione; to znaczy, są to kompleksy łańcuchowe. Dokładny trójkąt w D ( A ) to trójkąt, który jest izomorficzny w D
   ( ZA ) do trójkąta ${\ Displaystyle X \ do Y \ do {\ tekst {stożek}} (f) \ do X [1]}$ związany z jakąś mapą ${\ displaystyle f \ dwukropek X \ do Y}$ kompleksów łańcuchowych. Kluczową motywacją dla kategorii pochodnej jest to, że funktory pochodne na A mogą być postrzegane jako funktory na kategorii pochodnej. Niektóre naturalne podkategorie D ( A ) są również kategoriami triangulowanymi, na przykład podkategorią kompleksów X , których obiekty kohomologii w A znikają dla i wystarczająco negatywnego, wystarczająco pozytywnego lub obu, zwanych H. ja ${\ Displaystyle H ^ {i} (X$${\ Displaystyle D ^ {+} (A), D ^ {-} (A), D ^ {\ tekst {b}} (A) }$ odpowiednio.
4. W topologii stabilna kategoria homotopii $.$ kategorią Obiekty to widma , przesunięcie X [1] to zawieszenie (lub równoważnie opóźnienie $)$ i dokładne trójkąty $X}$ są sekwencjami cofiber. Charakterystyczną cechą stabilnej kategorii homotopii (w porównaniu z niestabilną kategorią homotopii ) jest to, że sekwencje włókien są takie same jak sekwencje kowłókna. W rzeczywistości, w dowolnej triangulowanej kategorii, dokładne trójkąty mogą być postrzegane jako sekwencje włókien, a także jako sekwencje włókien współwłóknistych.
5. W modułowej teorii reprezentacji skończonej grupy G stabilna kategoria modułowa StMod( kG ) jest kategorią triangulowaną. Jego obiektami są reprezentacje G na polu k , a morfizmy są zwykłymi morfizmami modulo tymi, które uwzględniają rzutowe (lub równoważnie iniekcyjne ) moduły kG . Mówiąc bardziej ogólnie, stabilna kategoria modułów jest zdefiniowana dla dowolnej algebry Frobeniusa zamiast kG .

Czy są lepsze aksjomaty?

Niektórzy eksperci podejrzewają , że ^{na str. 190} (patrz np. (Gelfand & Manin 2006 , Wprowadzenie, Rozdział IV)) kategorie triangulacyjne nie są tak naprawdę „właściwą” koncepcją. Zasadniczym powodem jest to, że stożek morfizmu jest unikalny tylko do nieunikalnego izomorfizmu. W szczególności stożek morfizmu na ogół nie zależy funkcjonalnie na morfizmie (zwróć na przykład uwagę na niejednoznaczność w aksjomacie (TR 3), na przykład). Ta nieunikalność jest potencjalnym źródłem błędów. Aksjomaty działają jednak odpowiednio w praktyce i istnieje wiele literatury poświęconej ich badaniu.

pochodne

Jedną z alternatywnych propozycji jest teoria derywatorów zaproponowana w Pursuing stacks przez Grothendiecka w latach 80. ^{s. 191} , a później rozwinięta w latach 90. w jego rękopisie na ten temat. $W$ są to systemy kategorii homotopii podane przez kategorie diagramów $(M, W)$ kategorii z klasą słabych równoważności . Kategorie te są następnie powiązane morfizmami diagramów ${\ Displaystyle I \ do J}$ . Ten formalizm ma tę zaletę, że jest w stanie odzyskać granice homotopii i kolimity, co zastępuje konstrukcję stożka.

Stabilne ∞-kategorie

Inną zbudowaną alternatywą jest teoria stabilnych ∞-kategorii . Kategoria homotopii stabilnej kategorii ∞ jest kanonicznie triangulowana, a ponadto czopki mapujące stają się zasadniczo unikalne (w precyzyjnym sensie homotopicznym). Co więcej, stabilna kategoria ∞ w naturalny sposób koduje całą hierarchię zgodności dla swojej kategorii homotopii, na dole której znajduje się aksjomat oktaedryczny. Zatem zdecydowanie silniejsze jest podanie danych stabilnej kategorii ∞ niż podanie danych triangulacji jej kategorii homotopii. Prawie wszystkie triangulowane kategorie, które pojawiają się w praktyce, pochodzą ze stabilnych ∞-kategorii. Podobnym (ale bardziej szczególnym) wzbogaceniem kategorii triangulowanych jest pojęcie a kategoria dg .

W pewnym sensie stabilne kategorie ∞ lub kategorie dg działają lepiej niż kategorie triangulowane. Jednym z przykładów jest pojęcie dokładnego funktora między triangulowanymi kategoriami, omówione poniżej. Dla gładkiej rozmaitości rzutowej $ograniczona$ na polu k , kategoria pochodna snopów kategorii w naturalny sposób. Dla rozmaitości X i Y każdy funktor z kategorii dg X do kategorii of Y pochodzi z kompleksu snopów na ${\ displaystyle X \ razy Y}$ przez transformatę Fouriera – Mukai . Dla kontrastu, istnieje przykład dokładnego funktora z ${\ Displaystyle {\ tekst {D}} ^ {\ tekst {b}} (X)}$ do ${\ Displaystyle {\ tekst {D}} ^ {\ tekst {b}} (Y)},$ który nie pochodzi z kompleksu snopów na ${\ Displaystyle X \ razy Y}$ . W świetle tego przykładu „właściwe” pojęcie morfizmu między triangulowanymi kategoriami wydaje się pochodzić z morfizmu podstawowych kategorii dg (lub stabilnych ∞-kategorii).

Kolejna przewaga stabilnych kategorii ∞ lub kategorii dg nad kategoriami triangulowanymi pojawia się w algebraicznej teorii K. Można zdefiniować algebraiczną teorię $K$ stabilnej kategorii ∞ lub kategorii dg podając grup abelowych liczb całkowitych . Grupa $C.$ prosty opis w kategoriach triangulowanej . Ale przykład pokazuje, że wyższe grupy K kategorii dg nie zawsze są określane przez powiązaną kategorię triangulowaną. Tak więc kategoria triangulowana ma dobrze zdefiniowaną $grupę$ ale generalnie nie wyższe grupy K.

Z drugiej strony teoria kategorii triangulowanych jest prostsza niż teoria stabilnych kategorii ∞ lub kategorii dg iw wielu zastosowaniach struktura triangulowana jest wystarczająca. Przykładem jest dowód hipotezy Blocha-Kato , gdzie wiele obliczeń przeprowadzono na poziomie kategorii triangulowanych, a dodatkowa struktura ∞-kategorii lub dg-kategorii nie była wymagana.

Kohomologia w triangulowanych kategoriach

Kategorie triangulowane dopuszczają pojęcie kohomologii, a każda kategoria triangulowana ma duży zapas funktorów kohomologicznych. Funktor kohomologiczny F od triangulowanej kategorii D do abelowej kategorii A jest funktorem takim, że dla każdego dokładnego trójkąta

${\ Displaystyle X \ do Y \ do Z \ do X [1], \}$

sekwencja w A jest dokładna ${\ Displaystyle F (X) \ do F (Y) \ do F (Z)} .$ Ponieważ dokładny trójkąt określa nieskończoną sekwencję dokładnych trójkątów w obu kierunkach,

${\ Displaystyle \ cdots \ do Z [-1] \ do X \ do Y \ do Z \ do X [1] \ do \cdots ,\ }$

funktor kohomologiczny F faktycznie daje długi dokładny ciąg w abelowej kategorii A :

${\ Displaystyle \ cdots \ do F (Z [-1]) \ do F (X) \ do F (Y) \ do F (Z) \ do F (X [1]) \ do \ cdots. \}$

Kluczowym przykładem jest: dla każdego obiektu B w triangulowanej kategorii D , funktory ${\ Displaystyle \ operatorname {Hom} (B, {\ tekst {-}})}$ i ${\ Displaystyle \ operatorname {Hom} ({\ tekst {-}}, B)}$ są kohomologiczne, z wartościami należącymi do kategorii grup abelowych . (Ściślej mówiąc, ten ostatni jest funktorem kontrawariantnym , który można uznać za funktor na przeciwna kategoria D . ) Oznacza to, że dokładny trójkąt określa dwie długie dokładne sekwencje grup abelowych: ${\ Displaystyle X \ do Y \ do Z \ do X [1]}$

${\ Displaystyle \ cdots \ do \ operatorname {Hom} (B, X [i]) \ do \ operatorname {Hom} (B, Y [i]) \ do \ operatorname {Hom} (B, Z [i]) \do \nazwa_operatora {Hom} (B,X[i+1])\do \cdots }$

I

${\ Displaystyle \ cdots \ do \ operatorname {Hom} (Z, B [i]) \ do \ operatorname {Hom} (Y, B [i]) \ do \ operatorname {Hom} (X, B [i]) \to \operatorname {Hom} (Z,B[i+1])\to \cdots .}$

W przypadku określonych triangulowanych kategorii te dokładne sekwencje dają wiele ważnych dokładnych sekwencji w kohomologii snopów, kohomologii grup i innych obszarach matematyki.

Można również użyć notacji

${\ Displaystyle \ operatorname {Ext} ^ {i} (B, X) = \ operatorname {Hom} (B, X [i]) }$

dla liczb całkowitych i , uogólniając funktor Ext w kategorii abelowej. W tym zapisie pierwsza dokładna sekwencja powyżej byłaby zapisana:

${\ Displaystyle \ cdots \ do \ nazwa operatora {zewn.} ^ {i} (B, X) \ do \ nazwa operatora {zewn} ^ {i} (B, Y) \ do \ nazwa operatora {zewn} ^ {i} (B ,Z)\do \nazwa_operatora {Ext} ^{i+1}(B,X)\do \cdots .\ }$

Dla kategorii abelowej $($ inny przykład funktora kohomologicznego w kategorii pochodnej re ZA ) wysyła X do obiektu A . $_$ dokładny trójkąt w D ( ZA A :

${\ Displaystyle \ cdots \ do H ^ {i} (X) \ do H ^ { i}(Y)\do H^{i}(Z)\do H^{i+1}(X)\do \cdots ,}$

używając tego ${\ Displaystyle H ^ {0} (X [i]) \ cong H ^ {i} (X)}$ .

Dokładne funktory i równoważności

Funktor dokładny (zwany także $jest$ triangulowanym ) z triangulowanej kategorii do triangulowanej kategorii E funktorem addytywnym, , luźno mówiąc, komutuje z tłumaczeniem i trójkąty na dokładne trójkąty.

Bardziej szczegółowo, dokładny funktor ma naturalny izomorfizm $F}$ gdzie pierwszy oznacza funktor translacyjny $\ dwukropek F \ Sigma \ do \ Sigma$ z D , a drugi oznacza funktor translacji E ), taki, że kiedykolwiek ${\ displaystyle \ Sigma}$

${\ Displaystyle X {\ xrightarrow {{} \ na szczycie u}} Y {\ xrightarrow {{} \ na szczycie v}} Z {\ xrightarrow {{} \ na szczycie w }}X[1]}$

jest dokładnym trójkątem w D ,

${\ Displaystyle F (X) {\ xrightarrow {F (u )}} F (Y) {\ xrightarrow {F (v)}} F (Z) {\ xrightarrow {\ eta _ {X} F (w)}} F (X) [1]}$

jest dokładnym trójkątem w E .

Równoważność triangulowanych kategorii jest dokładnym $również$ , kategorii W tym przypadku istnieje dokładny funktor taki, że $i$ GF są z funktorami tożsamości

Kompaktowo generowane triangulowane kategorie

Niech D będzie kategorią triangulowaną taką, że w D istnieją sumy bezpośrednie indeksowane przez dowolny zbiór (niekoniecznie skończony) . Obiekt X w D nazywany jest zwartym , jeśli funktor ${\ Displaystyle {\ tekst {Hom}} _ {D} (X, {\ tekst {-}})}$ dojeżdża z bezpośrednimi sumami. Wyraźnie oznacza to, że dla każdej rodziny obiektów w D indeksowanej przez zbiór ${\ displaystyle Y_ {i}}$ S , naturalny homomorfizm grup abelowych ${\ Displaystyle \ oplus _ {i \ w S} \ mathrm {Hom} _{D}(X,Y_{i})\to \mathrm {Hom} _{D}(X,\oplus _{i\in S}Y_{i})} jest izomorfizmem$ . Różni się to od ogólnego pojęcia zwartego obiektu w teorii kategorii, która obejmuje wszystkie współograniczenia, a nie tylko koprodukty.

Na przykład zwarty obiekt w stabilnej kategorii homotopii $.$ skończonym Zwarty obiekt w pochodnej kategorii pierścienia lub w quasi-koherentnej kategorii pochodnej schematu jest złożeniem doskonałym . W przypadku gładkiej rozmaitości rzutowej X na polu, kategorię Perf( X ) kompleksów doskonałych można również postrzegać jako ograniczoną pochodną kategorię spójnych snopów, ${\ Displaystyle D _ {\ tekst {coh}} ^ {\ tekst {b}} (X)}$ .

Triangulowana kategoria D jest generowana zwięźle, jeśli

• D ma dowolne (niekoniecznie skończone) sumy bezpośrednie;
• Istnieje zbiór S zwartych obiektów w D taki, że dla każdego niezerowego obiektu X w D istnieje obiekt Y w S z niezerową mapą ${\ Displaystyle Y [n] \ do X$ } liczba całkowita n .

Wiele naturalnie występujących „dużych” trójkątnych kategorii jest generowanych zwartie:

• Pochodna kategoria modułów na pierścieniu R jest generowana zwięźle przez jeden obiekt, R -moduł R .
• Quasi-spójna kategoria pochodna schematu quasi-zwartego quasi-rozdzielonego jest generowana zwięźle przez jeden obiekt.
• Stabilna kategoria homotopii jest zwięźle generowana przez jeden obiekt, widmo sferyczne . ${\ displaystyle S ^ {0}}$ .

Amnon Neeman uogólnił twierdzenie Browna o reprezentowalności na dowolną zwarto generowaną kategorię triangulowaną w następujący sposób. Niech D będzie $.$ kategorią triangulowaną, kohomologicznym, który przenosi Wtedy H jest reprezentowalne. (Oznacza to, że istnieje obiekt W z D taki, że ${\ Displaystyle H (X) \ cong {\ tekst {Hom}} (X, W)}$ dla wszystkich X .) W innej wersji niech D będzie generowaną kompaktowo kategorią triangulowaną, T dowolną kategorią triangulowaną. Jeśli dokładny funktor $do$ koprodukty , to F prawe

Twierdzenie Browna o reprezentatywności może być użyte do zdefiniowania różnych funktorów między triangulowanymi kategoriami. W szczególności Neeman użył go do uproszczenia i uogólnienia konstrukcji wyjątkowego odwrotnego funktora obrazu $\ displaystyle f ^ {!}}$ { dla morfizmu f schematów , centralnej cechy spójnej teorii dualności .

struktury t

Główny artykuł: struktura t

Dla każdej kategorii abelowej A , kategoria pochodna D ( A ) jest kategorią triangulowaną, zawierającą A jako pełną podkategorię (zespoły skoncentrowane w stopniu zero). Różne kategorie abelowe mogą mieć równoważne kategorie pochodne, więc nie zawsze jest możliwe zrekonstruowanie A z D ( A ) jako kategorii triangulowanej.

Alexander Beilinson , Joseph Bernstein i Pierre Deligne opisali tę sytuację za pomocą pojęcia struktury t na triangulowanej kategorii D. Struktura t na D określa kategorię abelową wewnątrz D , a różne struktury t na D mogą dawać różne kategorie abelowe.

Lokalizowanie i grube podkategorie

Niech D będzie kategorią triangulowaną z dowolnymi sumami prostymi. Lokalizująca podkategoria D jest ściśle w pełni triangulowaną podkategorią, która jest zamknięta w dowolnych bezpośrednich sumach . Aby wyjaśnić nazwę: jeśli lokalizacyjna podkategoria S zwarto wygenerowanej trójkątnej kategorii D jest generowana przez zbiór obiektów, to istnieje funktor lokalizacji Bousfielda z jądrem ${\ displaystyle L \ dwukropek D \ do D}$ S . (Oznacza to, że dla każdego obiektu X w D istnieje dokładny trójkąt ${\ Displaystyle Y \ do X \ do LX \ do Y [1]}$ z Y w S i LX w prawy ortogonalny ${\ Displaystyle S ^ {\ perp}}$ .) Na przykład ta konstrukcja obejmuje lokalizację widma na liczbie pierwszej lub ograniczenie z kompleksu snopów na przestrzeni do otwartego podzbioru.

Pojęcie równoległe jest bardziej odpowiednie dla „małych” triangulowanych kategorii: gruba podkategoria triangulowanej kategorii C jest podkategorią ściśle triangulowaną, która jest zamknięta na bezpośrednie sumy. (Jeśli C jest idempotent-complete , podkategoria jest gruba wtedy i tylko wtedy, gdy jest również idempotent-complete.) Podkategoria lokalizacyjna jest gruba. Więc jeśli S jest lokalizującą podkategorią triangulowanej kategorii D , to przecięcie S z podkategorią ${\ Displaystyle D ^ {\ text {c}}}$ obiektów zwartych to gruba podkategoria re do $^ {\ text {c}}}$ .

Na przykład Devinatz- Hopkins -Smith opisał wszystkie grube podkategorie triangulowanej kategorii skończonych widm w kategoriach K-teorii Morawy . Lokalizujące podkategorie całej kategorii stabilnej homotopii nie zostały sklasyfikowane.

Zobacz też

• Transformata Fouriera-Mukai
• Sześć operacji
• Przewrotny snop
• Moduł D
• Lokalizacja Beilinsona-Bernsteina
• Widmo modułu
• Dekompozycja semiortogonalna
• Warunek stateczności Bridgelanda

Notatki

Niektóre podręcznikowe wprowadzenia do triangulowanych kategorii to:

•    Gelfand, Siergiej; Manin, Yuri (2006), „IV. Kategorie triangulowane”, Metody algebry homologicznej , Springer Monographs in Mathematics (wyd. 2), Springer-Verlag , doi : 10.1007/978-3-662-12492-5 , ISBN 978- 3540435839 , MR 1950475
•    Kashiwara, Masaki ; Schapira, Pierre (2006), Kategorie i snopy , Grundlehren der mathematischen Wissenschaften, Berlin, New York: Springer-Verlag , doi : 10.1007/3-540-27950-4 , ISBN 978-3-540-27949-5 , MR 2182076
•     Weibel, Charles A. (1994). Wprowadzenie do algebry homologicznej . Cambridge Studies in Advanced Mathematics. Tom. 38. Cambridge University Press. ISBN 978-0-521-55987-4 . MR 1269324 . OCLC 36131259 .

Zwięzłe podsumowanie z aplikacjami to:

•    Kashiwara, Masaki ; Schapira, Pierre (2002), „ROZDZIAŁ I. HOMOLOGALNA Algebra”, Sheves na kolektorach , Grundlehren der Mathematischen Wissenschaften, Springer-Verlag , doi : 10.1007/978-3-662-02661-8 , ISBN 978-3540518617 , MR 1074006

Niektóre bardziej zaawansowane odniesienia to:

•    Beilinson, AA ; Bernstein, J .; Deligne, P. (2018) [1982], "Faisceaux pervers" , Astérisque , Société Mathématique de France, Paryż, 100 , ISBN 978-2-85629-878-7 , MR 0751966
•   Dugger, Daniel; Shipley, Brooke (2009), „Ciekawy przykład trójkątnych równoważnych kategorii modeli, które nie są odpowiednikami Quillena”, Algebraic and Geometric Topology , 9 : 135–166, arXiv : 0710,3070 , doi : 10,2140/agt.2009.9.135 , MR 2482071
•    Hartshorne, Robin (1966), „Rozdział I. Kategoria pochodna”, Reszty i dwoistość , Lecture Notes in Mathematics 20 , Springer-Verlag , s. 20–48, doi : 10.1007 / BFb0080482 , ISBN 978-3-540-03603 -6 , MR 0222093
•   Krause, Henning (2010), „Teoria lokalizacji dla kategorii triangulowanych”, Kategorie triangulowane , seria notatek z wykładów London Mathematical Society, tom. 375, Cambridge University Press, s. 161–235, arXiv : 0806.1324 , doi : 10.1017/CBO9781139107075.005 , MR 2681709
•   Neeman, Amnon (1996), „Twierdzenie o dualności Grothendiecka za pomocą technik Bousfielda i reprezentacji Browna”, Journal of the American Mathematical Society , 9 : 205–236, doi : 10.1090 / S0894-0347-96-00174-9 , MR 1308405
•    Neeman, Amnon (2001), kategorie triangulowane , Annals of Mathematics Studies , Princeton University Press, doi : 10.1515/9781400837212 , ISBN 978-0691086866 , MR 1812507
•   Puppe, Dieter (1962), „O formalnej strukturze stabilnej teorii homotopii”, Colloquium on algebraic topology , Aarhus Universitet Matematisk Institute, s. 65–71, Zbl 0139.41106
•   Puppe, Dieter (1967), "Stale Homotopietheorie. I.", Mathematische Annalen , 169 : 243–274, doi : 10.1007/BF01362348 , MR 0211400
•    Ravenel, Douglas (1992), Nilpotencja i okresowość w stabilnej teorii homotopii , Princeton University Press, ISBN 9780691025728 , MR 1192553
•   Rizzardo, Alicja; Van den Bergh, Michel ; Neeman, Amnon (2019), „Przykład funktora innego niż Fouriera-Mukai między pochodnymi kategoriami spójnych snopów”, Inventiones Mathematicae , 216 : 927–1004, arXiv : 1410,4039 , doi : 10,1007/s00222-019-00862-9 , MR 3955712
•   Toën, Bertrand (2007), „Teoria homotopii kategori dg i pochodna teoria Mority”, Inventiones Mathematicae , 167 : 615–667, arXiv : math/0408337 , doi : 10.1007/s00222-006-0025-y , MR 2276263
•    Verdier, Jean-Louis (1977) [1963], „Categories dérivées: quelques résultats (état 0)” , Cohomologie étale (SGA 4 1/2) (PDF) , Notatki z wykładów z matematyki, tom. 569, Springer, s. 262–311, doi : 10.1007/BFb0091525 , ISBN 978-3-540-08066-4 , MR 3727440
•   Verdier, Jean-Louis (1996) [1967] Des catégories dérivées des catégories abéliennes , Astérisque, tom. 239, Société Mathématique de France, MR 1453167

Linki zewnętrzne

• J. Peter May , Aksjomaty kategorii triangulowanych
• Autorzy projektu Stacks, Projekt Stacks