Funktor zewnętrzny
W matematyce funktory Ext są funktorami pochodnymi funktora Hom . Wraz z funktorem Tor , Ext jest jednym z podstawowych pojęć algebry homologicznej , w której idee z topologii algebraicznej są używane do definiowania niezmienników struktur algebraicznych. Kohomologię grup , algebry Liego i algebry asocjacyjne można zdefiniować za pomocą Ext. Nazwa wzięła się stąd, że pierwsza grupa Ext Ext 1 klasyfikuje rozszerzenia jednego modułu przez inny.
W szczególnym przypadku grup abelowych Ext został wprowadzony przez Reinholda Baera (1934). Został nazwany przez Samuela Eilenberga i Saundersa MacLane'a (1942) i zastosowany do topologii ( twierdzenie o uniwersalnym współczynniku dla kohomologii ). Dla modułów na dowolnym pierścieniu , Ext zostało zdefiniowane przez Henri Cartana i Eilenberga w ich książce Homological Algebra z 1956 roku .
Definicja
Niech R będzie pierścieniem i niech R -Mod będzie kategorią modułów nad R . (Można przyjąć, że oznacza to albo lewe R , albo prawe moduły R. ) Dla ustalonego modułu R A niech T ( B ) = Hom R ( A , B ) dla B w R -Mod. (Tutaj Hom R ( A , B ) jest abelową grupą R -liniowych odwzorowań od A do B ; jest to R -moduł, jeśli R jest przemienny .) Jest to lewy funktor dokładny z R -Mod do kategorii abelowych grup Ab, a więc ma funktory wyprowadzone w prawo R i T . Grupy Ext to grupy abelowe zdefiniowane przez
dla liczby całkowitej i . Z definicji oznacza to: weź dowolną rozdzielczość iniekcyjną
usuń termin B i utwórz kompleks kołańcuchowy :
0 Dla każdej liczby całkowitej i , Ext
i R ( A , B ) jest kohomologią tego kompleksu w pozycji i . Jest zero dla i ujemne. Na przykład Ext 0
R ( A , B ) jest jądrem mapy Hom R ( A , I ) → Hom R ( A , I 1 ), która jest izomorficzna z Hom R ( A , B ).
Alternatywna definicja używa funktora G ( A )=Hom R ( A , B ) dla stałego R - modułu B. Jest to funktor kontrawariantny , który można postrzegać jako lewy funktor dokładny z przeciwnej kategorii ( R -Mod) op do Ab. Grupy Ext są zdefiniowane jako prawe funktory pochodne R i G :
Oznacza to, że wybierz dowolną rozdzielczość projekcyjną
usuń termin A i utwórz kompleks kołańcuchowy:
Wtedy Ext
i R ( A , B ) jest kohomologią tego kompleksu w pozycji i .
Cartan i Eilenberg wykazali, że konstrukcje te są niezależne od wyboru rozdzielczości rzutowej lub iniekcyjnej i że obie konstrukcje dają te same grupy Ext. Ponadto dla ustalonego pierścienia R Ext jest funktorem w każdej zmiennej (kontrawariantny w A , kowariantny w B ).
Dla pierścienia przemiennego R i R -moduły A i B , Ext
i R ( A , B ) jest R -modułem (używając tego, że Hom R ( A , B ) jest w tym przypadku R -modułem). Dla nieprzemiennego pierścienia R , Ext
i R ( A , B ) jest ogólnie tylko grupą abelową. Jeśli R jest algebrą na pierścieniu S (co oznacza w szczególności, że S jest przemienny), to Ext
i R ( A , B ) jest co najmniej S -modułem.
Właściwości zewn
Oto niektóre z podstawowych właściwości i obliczeń grup Ext.
- Ext 0
R ( A , B ) ≅ Hom R ( A , B ) dla dowolnych modułów R A i B .
- Ext
i R ( A , B ) = 0 dla wszystkich i > 0 jeśli moduł R A jest rzutowy (na przykład wolny ) lub jeśli B jest iniekcyjny .
- Conversy posiadają również:
- Jeśli Ext
1 R ( A , B ) = 0 dla wszystkich B , to A jest rzutowe (a zatem Ext
i R ( A , B ) = 0 dla wszystkich i > 0). - Jeśli Ext
1 R ( A , B ) = 0 dla wszystkich A , to B jest iniekcyjne (a zatem Ext
i R ( A , B ) = 0 dla wszystkich i > 0).
- Jeśli Ext
- dla wszystkich ja ≥ 2 i wszystkich grup abelowych A i B .
- Jeśli R jest pierścieniem przemiennym, a u w R nie jest dzielnikiem zera , to
- dla dowolnego modułu R B . Tutaj B [ u ] oznacza podgrupę u -torsji B , { x ∈ B : ux = 0}. Biorąc R za pierścień całkowitych, to obliczenie można wykorzystać do obliczenia dla dowolnej skończenie wygenerowanej grupy abelowej A .
- Uogólniając poprzedni przykład, można obliczyć grupy Ext, gdy pierwszym modułem jest iloraz pierścienia przemiennego przez dowolny ciąg regularny , używając kompleksu Koszula . Na przykład, jeśli R jest pierścieniem wielomianowym k [ x 1 ,..., x n ] nad ciałem k , to Ext
* R ( k , k ) jest zewnętrzną algebrą S nad k na n generatorach w Ext 1 . Ponadto Ext
* S ( k , k ) jest pierścieniem wielomianowym R ; jest to przykład dwoistości koszulskiej .
- Z ogólnych właściwości funktorów pochodnych wynika, że istnieją dwa podstawowe ciągi dokładne dla Ext. Po pierwsze, krótki ciąg dokładny 0 → K → L → M → 0 R -modułów indukuje długi ciąg dokładny postaci
- dla dowolnego modułu R A . Również krótki ciąg dokładny 0 → K → L → M → 0 indukuje długi ciąg dokładny postaci
- dla dowolnego modułu R B .
- Ext bierze bezpośrednie sumy (prawdopodobnie nieskończone) w pierwszej zmiennej i iloczyny w drugiej zmiennej do produktów. To jest:
- Niech A będzie skończenie generowanym modułem na przemiennym pierścieniu noetherowskim R . Wtedy Ext komutuje z lokalizacją w tym sensie, że dla każdego multiplikatywnie domkniętego zbioru S w R , każdego R -modułu B i każdej liczby całkowitej i ,
Rozszerzenia i rozszerzenia
Równoważność rozszerzeń
Grupy Ext wywodzą swoją nazwę od ich stosunku do rozszerzeń modułów. Biorąc pod uwagę R -moduły A i B , rozszerzenie A przez B jest krótką dokładną sekwencją R -modułów
Dwa rozszerzenia
mówi się, że są równoważne (jako rozszerzenia A przez B ), jeśli istnieje diagram przemienny :
Zauważ, że lemat o pięciu implikuje, że środkowa strzałka jest izomorfizmem. Przedłużenie A przez B nazywa się podziałem , jeśli jest równoważne trywialnemu rozszerzeniu
Istnieje zgodność jeden do jednego między klasami równoważności rozszerzeń A przez B i elementami Ext
1 R ( A , B ). Trywialne rozszerzenie odpowiada elementowi zerowemu Ext
1 R ( A , B ).
Suma Baera rozszerzeń
Suma Baera jest wyraźnym opisem struktury grup abelowych na Ext
1 R ( A , B ), postrzeganej jako zbiór klas równoważności rozszerzeń A przez B . Mianowicie, biorąc pod uwagę dwa rozszerzenia
I
najpierw utwórz wycofanie ponad }
Następnie utwórz moduł ilorazu
Suma Baera E i E ′ jest rozszerzeniem
gdzie pierwsza mapa to a drugi to .
Aż do równoważności rozszerzeń suma Baera jest przemienna i ma trywialne rozszerzenie jako element tożsamości. Ujemne rozszerzenie 0 → B → E → A → 0 jest rozszerzeniem obejmującym ten sam moduł E , ale z homomorfizmem B → E zastąpionym jego ujemnym.
Konstrukcja Ext w kategoriach abelowych
Nobuo Yoneda zdefiniował grupy abelowe Ext
n C ( A , B ) dla obiektów A i B w dowolnej kategorii abelowej C ; zgadza się to z definicją pod względem rozdzielczości, jeśli C ma wystarczającą liczbę rzutów lub wystarczającą liczbę iniekcji . Po pierwsze, Ext 0
C ( A , B ) = Hom C ( A , B ). Następnie Ext
1 C ( A , B ) jest zbiorem klas równoważności rozszerzeń A przez B , tworzących grupę abelową pod sumą Baera. Wreszcie wyższe grupy Ext Ext
n C ( A , B ) są zdefiniowane jako klasy równoważności n-rozszerzeń , które są dokładnymi sekwencjami
w ramach relacji równoważności generowanej przez relację identyfikującą dwa rozszerzenia
jeśli istnieją mapy dla wszystkich m w {1, 2, ..., , że każdy wynikowy do pracy to , jeśli istnieje mapa łańcucha ξ → ξ', która jest tożsamością na A i B .
Suma Baera dwóch - rozszerzeń jak powyżej tworzona przez pozwolenie na wycofanie X 1 i być wypchnięciem X n X } pod B . Wtedy suma Baera rozszerzeń wynosi
Kategoria pochodna i produkt Yoneda
Ważną kwestią jest to, że grupy Ext w kategorii abelowej C można postrzegać jako zbiory morfizmów w kategorii powiązanej z C , kategorii pochodnej D ( C ). Obiektami kategorii pochodnej są kompleksy obiektów w C. Konkretnie, jeden ma
gdzie obiekt C jest postrzegany jako kompleks skoncentrowany w stopniu zero, a [ i ] oznacza przesunięcie kompleksu i krokami w lewo. Z tej interpretacji wynika mapa dwuliniowa , czasami nazywana iloczynem Yoneda :
który jest po prostu złożeniem morfizmów w kategorii pochodnej.
Produkt Yoneda można też opisać bardziej elementarnie. Dla i = j = 0 produktem jest złożenie map w kategorii C . Ogólnie rzecz biorąc, produkt można zdefiniować, łącząc ze sobą dwa przedłużenia Yoneda.
Alternatywnie produkt Yoneda można zdefiniować w kategoriach rozdzielczości. (Jest to zbliżone do definicji kategorii pochodnej.) Na przykład, niech R będzie pierścieniem z R -modułami A , B , C , i niech P , Q i T będą rzutowymi rozdzielczościami A , B , C . Wówczas Ext
i R ( A , B ) można utożsamiać z grupą klas homotopii łańcuchów map łańcuchowych P → Q [ i ]. Produkt Yoneda jest podawany poprzez komponowanie map łańcucha:
W dowolnej z tych interpretacji produkt Yoneda jest asocjacyjny. W rezultacie pierścieniem _ _ _ _ _ Na przykład daje to strukturę pierścienia na kohomologii grupowej ponieważ można to postrzegać jako . Również przez asocjatywność produktu Yoneda: dla dowolnych modułów R A i B , jest moduł nad .
Ważne przypadki szczególne
- H. = , gdzie G jest grupą, M jest reprezentacją G na liczbach całkowitych i to pierścień grupy G .
- Dla algebry A na polu k i A - bimodułu M , kohomologia Hochschilda jest zdefiniowana przez
- Kłamstwo kohomologia przez gdzie jest algebrą Liego przemiennym pierścieniu k , M jest moduł jest uniwersalną algebrą obwiedni
- Dla przestrzeni topologicznej X snopów można zdefiniować jako A kategorii snopów abelowych na X , a snopem funkcji o wartościach stałych
- Dla przemiennego lokalnego pierścienia Noetherowskiego R z polem reszt k , jest uniwersalną algebrą obejmującą a stopniowana algebra Liego π*( R ) nad k , znana jako homotopia algebry Liego R . (Mówiąc precyzyjnie, gdy k ma charakterystykę 2, π * ( R ) należy postrzegać jako „dostosowaną algebrę Liego”.) Istnieje naturalny homomorfizm stopniowanych algebr Liego z kohomologii André – Quillena D * ( k / R , k ) do π*( R ), co jest izomorfizmem, jeśli k ma charakterystyczne zero.
Zobacz też
Notatki
- Avramov, Luchezar (2010), „Nieskończone wolne rozdzielczości”, Sześć wykładów z algebry przemiennej , Birkäuser , s. 1–108, doi : 10.1007 / 978-3-0346-0329-4_1 , ISBN 978-3-7643-5951- 5 , MR 2641236
- Baer, Reinhold (1934), „Erweiterung von Gruppen und ihren Isomorphismen”, Mathematische Zeitschrift , 38 (1): 375–416, doi : 10.1007/BF01170643 , Zbl 0009.01101
- Cartan, Henri ; Eilenberg, Samuel (1999) [1956], algebra homologiczna , Princeton: Princeton University Press , ISBN 0-691-04991-2 , MR 0077480
- Eilenberg, Samuel ; MacLane, Saunders (1942), „Rozszerzenia grup i homologia”, Annals of Mathematics , 43 (4): 757–931, doi : 10.2307/1968966 , JSTOR 1968966 , MR 0007108
- Gelfand, Siergiej I.; Manin, Jurij Iwanowicz (2003), Metody algebry homologicznej , Berlin, Nowy Jork: Springer-Verlag , doi : 10.1007/978-3-662-12492-5 , ISBN 978-3-540-43583-9 , MR 1950475
- Sjödin, Gunnar (1980), „Algebry Hopfa i pochodne”, Journal of Algebra , 64 : 218–229, doi : 10.1016/0021-8693 (80) 90143-X , MR 0575792
- Weibel, Charles A. (1994). Wprowadzenie do algebry homologicznej . Cambridge Studies in Advanced Mathematics. Tom. 38. Cambridge University Press. ISBN 978-0-521-55987-4 . MR 1269324 . OCLC 36131259 .
- Weibel, Charles A. (1999), „Historia algebry homologicznej” (PDF) , Historia topologii , Amsterdam: North-Holland, s. 797–836, ISBN 9780444823755 , MR 1721123







![{\displaystyle \operatorname {Ext} _{R}^{i}(R/(u),B)\cong {\begin{cases}B[u]&i=0\\B/uB&i=1\\0&{\text{otherwise,}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d29b19b92e3188770f876e89fe5d69f61f2bb030)









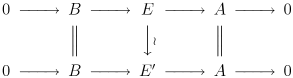

![{\displaystyle 0\to B{\xrightarrow[{f}]{}}E{\xrightarrow[{g}]{}}A\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99b91ef9769c22705bb158052b57276636e7906c)
![{\displaystyle 0\to B{\xrightarrow[{f'}]{}}E'{\xrightarrow[{g'}]{}}A\to 0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3c3b1f07bd8dcc1d933bb0a1b72b397a6e885e9)




![b\mapsto [(f(b),0)]=[(0,f'(b))]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee75b87481bf9de19754e30ff4b98f9e3a93c53f)











![{\displaystyle \operatorname {Ext} _{\mathbf {C} }^{i}(A,B)=\operatorname {Hom} _{D({\mathbf {C} })}(A,B[i]),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd4f0a89006dc8d51c99160bf062be7b92891c2f)

![{\displaystyle P\to Q[i]\to T[i+j].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e1db5574c44feacd2e3448b888bb92c98bb8c17)


![{\displaystyle \operatorname {Ext} _{\mathbb {Z} [G]}^{*}(\mathbb {Z} ,\mathbb {Z} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caa2d03e117e399c9fc5a96b1e4383be50277a2b)

![{\displaystyle H^{*}(G,M)=\operatorname {Ext} _{\mathbb {Z} [G]}^{*}(\mathbb {Z} ,M)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75ea5c28b67c0bc2f3dea33b55aa97d33977f830)
![{\displaystyle \mathbb {Z} [G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f40260c366fc309a5872899d2ea34cf094855857)






