Obiekt iniekcyjny

W matematyce , zwłaszcza w dziedzinie teorii kategorii , pojęcie przedmiotu iniekcyjnego jest uogólnieniem pojęcia modułu iniekcyjnego . Pojęcie to jest ważne w kohomologii , w teorii homotopii iw teorii kategorii modelowych . Podwójne pojęcie to pojęcie obiektu projekcyjnego .

Definicja

Obiekt Q jest iniekcyjny, jeśli przy danym monomorfizmie f : X → Y dowolny g : X → Q można rozszerzyć do Y .

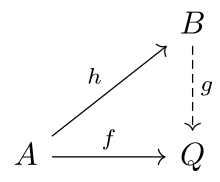
O obiekcie w kategorii mówi się, że jest iniekcyjny $\ displaystyle Q$ jeśli dla każdego $i$ każdego $g$ dla każdego morfizmu ${\ Displaystyle g: X \ do Q}$ istnieje morfizm ${\ Displaystyle h: Y \ do Q}$ rozszerzający ${\ displaystyle g}$ do ${\ displaystyle Y}$ , tj. takie, że ${\ displaystyle h \ circ f = g}$ .

$X \ do Q}$ to, że każdy morfizm uwzględnia każdy monomorfizm $displaystyle$ .

Morfizm w $powyższej$$definicji$ nie musi być $jednoznacznie$ i .

W lokalnie małej kategorii jest to równoważne wymaganiu, aby funktor hom ${\ Displaystyle \ operatorname {Hom} _ {\ mathbf {C}} (-, Q)}$ niósł monomorfizmy w ${ \displaystyle \mathbf {C}}$ do surjektywnych map zbiorów.

W kategoriach abelowych

Pojęcie iniekcji zostało po raz pierwszy sformułowane dla kategorii abelowych i nadal jest to jeden z głównych obszarów jego zastosowania. Kiedy _{jest kategorią} $abelową$ , obiekt Q z jest iniekcyjny wtedy i tylko wtedy, gdy $funktor$ hom Hom C –, Q ) jest dokładny .

Jeśli $\ do U \ do V \ do 0}$$jest$ dokładną sekwencją w takiej, że Q jest iniekcyjne, to sekwencja się dzieli .

Dość wtryskiwaczy i łusek wtryskowych

Mówi się, że $istnieje$ ma wystarczającą liczbę iniekcji $,$ jeśli dla każdego obiektu X z monomorfizm od do obiektu iniekcji.

Monomorfizm g w nazywany jest monomorfizmem podstawowym , jeśli dla dowolnego morfizmu f złożony $jest$ jest monomorfizmem tylko wtedy, gdy f monomorfizmem .

Jeśli g jest podstawowym monomorfizmem z domeną X i iniekcyjną kodomeną G , to G nazywa się iniekcyjnym kadłubem X . Kadłub iniekcyjny jest wtedy jednoznacznie określony przez X aż do niekanonicznego izomorfizmu.

Przykłady

• W kategorii grup abelowych i homomorfizmów grupowych Ab obiekt iniekcyjny jest z konieczności grupą podzielną . Zakładając aksjomat wyboru, pojęcia są równoważne.
• W kategorii (lewych) modułów i homomorfizmów modułów , R - Mod , obiekt iniekcyjny jest modułem iniekcyjnym . R - Mod ma kadłuby iniekcyjne (w konsekwencji R - Mod ma wystarczającą ilość iniekcji).
• W kategorii przestrzeni metrycznych Met obiekt iniekcyjny jest przestrzenią iniekcyjną metryczną , a iniekcyjnym szkieletem przestrzeni metrycznej jest jej ciasna rozpiętość .
• W kategorii przestrzeni T ₀ i odwzorowań ciągłych obiekt iniekcyjny jest zawsze topologią Scotta na sieci ciągłej , a zatem jest zawsze trzeźwy i lokalnie zwarty .

Używa

Jeśli kategoria abelowa ma wystarczającą liczbę iniekcji, możemy utworzyć rezolucje iniekcyjne , tj. dla danego obiektu X możemy utworzyć długi ciąg dokładny

${\ Displaystyle 0 \ do X \ do Q ^ {0} \ do Q ^ {1} \ do Q ^ {2} \ do \ cdots}$

a następnie można zdefiniować pochodne funktory danego funktora F , stosując F do tej sekwencji i obliczając homologię wynikowej (niekoniecznie dokładnej) sekwencji. Podejście to jest używane do definiowania Ext i Tor , a także różnych teorii kohomologii w teorii grup , topologii algebraicznej i geometrii algebraicznej . Stosowane kategorie to zazwyczaj kategorie funktorów lub kategorie snopów O Moduły _X nad pewną przestrzenią pierścieniową ( X , O _X ) lub, bardziej ogólnie, dowolną kategorią Grothendiecka .

Uogólnienie

Obiekt Q jest H -injektywny, jeśli przy danym h : A → B w H , dowolne f : A → Q rozkłada się przez h .

Niech będzie $kategorią$ i niech $będzie$ klasą morfizmów z do $\ mathbf {C}$ displaystyle .

Mówi się, że obiekt jest $}$$do$ jeśli dla $} :$ każdego $morfizmu$ fa $}$$H.$ i każdy morfizm w ${\ mathcal {H}}}$ morfizm ${\ Displaystyle g: B \ do Q}$ z ${\ Displaystyle g \ circ h = f}$ .

Jeśli jest klasą monomorfizmów , wracamy do obiektów iniekcyjnych, które zostały omówione $.$

Mówi się, że wystarczającą $kategoria$ iniekcji ma $C}}$$,$ jeśli dla każdego obiektu X z istnieje do H ${\ Displaystyle {\ mathcal {H}}}$ -morfizm od X do -injective obiektu $\ Displaystyle {\ mathcal {H}}} .$

ZA ${\ Displaystyle {\ mathcal {H}}}$ -morfizm sol w do {\ Displaystyle \ mathbf { $}}$ nazywa się ${\ Displaystyle {\ mathcal {H}}}$ -istotny, jeśli dla dowolnego morfizmu f , złożony fg jest w tylko wtedy, gdy ${\ mathcal {H}}$ { \ $}$ .

Jeśli g jest -istotnym morfizmem z domeną $G$ i -injective codomain , to G nazywa się ${\mathcal {H}}}$ kadłub ${\ displaystyle {$$displaystyle$ -iniekcyjny X .

Przykłady obiektów iniekcyjnych H

• W kategorii zbiorów uproszczonych $obiekty iniekcyjne w odniesieniu$ do klasy rozszerzeń anodynowych to kompleksy Kan
• W kategorii częściowo uporządkowanych zbiorów i map monotonicznych kompletne kraty tworzą obiekty iniekcyjne dla klasy osadzania porządku , a uzupełnienie częściowo uporządkowanego zestawu przez Dedekinda-MacNeille'a to ${\ displaystyle {\ mathcal {H}}}$ jego $kadłub$ .

Zobacz też

• Obiekt projekcyjny

Notatki

• Jiri Adamek, Horst Herrlich, George Strecker. Kategorie abstrakcyjne i konkretne: Radość kotów, rozdział 9, Obiekty iniekcyjne i istotne osadzenia, ponownie opublikowane w przedrukach i zastosowaniach kategorii, nr 17 (2006) s. 1-507 , Wiley (1990).
• J. Rosicky, Iniekcja i dostępne kategorie
• ₀ F. Cagliari i S. Montovani, T -refleksyjne i iniekcyjne łuski przestrzeni światłowodowych