Macierzowa reprezentacja przekrojów stożkowych

W matematyce macierzowa reprezentacja przekrojów stożkowych umożliwia wykorzystanie narzędzi algebry liniowej do badania przekrojów stożkowych . Zapewnia łatwe sposoby obliczania osi przekroju stożkowego , wierzchołków , stycznych oraz biegunów i relacji biegunowych między punktami i liniami płaszczyzny określonej przez stożek. Technika ta nie wymaga umieszczania równania przekroju stożkowego w postaci standardowej, co ułatwia badanie tych przekrojów stożkowych, których osie nie są równolegle do układu współrzędnych .

Przekroje stożkowe (w tym zdegenerowane ) to zbiory punktów, których współrzędne spełniają równanie wielomianowe drugiego stopnia w dwóch zmiennych,

$\ Displaystyle Q (x, y) = Ax ^ {2} + Bxy + Cy ^ { 2}+Dx+Ey+F=0.}$

Przez nadużycie notacji ten przekrój stożkowy będzie również nazywany Q , gdy nie może dojść do pomyłki.

To równanie można zapisać w notacji macierzowej , w postaci macierzy symetrycznej, aby uprościć niektóre kolejne wzory, np

${\ Displaystyle \ lewo ({\ rozpocząć {macierz} x & y \ koniec {macierz} }\right)\left({\begin{macierz}A&B/2\\B/2&C\end{macierz}}\right)\left({\begin{macierz}x\\y\end{macierz}}\ right)+\left({\begin{macierz}D&E\end{macierz}}\right)\left({\begin{matrix}x\\y\end{macierz}}\right)+F=0.}$

Suma trzech pierwszych wyrazów tego równania, tj

${\ Displaystyle Ax ^ {2} + Bxy + Cy ^ {2} = \ lewo ({\begin{matrix}x&y\end{matrix}}\right)\left({\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right)\left({\begin{ macierz}x\\y\koniec{macierz}}\prawo),}$

jest formą kwadratową powiązaną z równaniem i macierzą

${\ Displaystyle A_ {33} = \ lewo ({\ rozpocząć {macierz} A & B / 2 \\ B / 2 i C \ koniec {matrycy}} \ prawej)}$

nazywa się macierzą postaci kwadratowej . Ślad i wyznacznik są niezmienne w odniesieniu do obrotu osi i $translacji$ ( ruch początku .

Równanie kwadratowe można również zapisać jako

${\ Displaystyle \ mathbf {x} ^ {T} A_ {Q} \ mathbf {x} = 0,}$

gdzie jest jednorodnym wektorem współrzędnych w trzech zmiennych ograniczonych tak, że ostatnia zmienna to 1, tj. x {\ $Displaystyle \ mathbf {x}$

${\ Displaystyle {\ rozpocząć {pmatrix} x \\ y \\ 1 \ koniec {pmatrix}}}$

i gdzie $_$

${\ Displaystyle A_ {Q} = {\ początek {pmatrix} A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\koniec {pmatrix}}.}$

Macierz $nazywana$ macierzą kwadratowego . Podobnie jak w przypadku $obrotu,$ i translacji.

Lewa górna podmacierz 2 × 2 (macierz rzędu 2) A _Q , uzyskana przez usunięcie trzeciego (ostatniego) wiersza i trzeciej (ostatniej) kolumny z A _Q jest macierzą postaci kwadratowej. Powyższa notacja A ₃₃ jest używana w tym artykule dla podkreślenia tej zależności.

Klasyfikacja

Q _Właściwe (niezdegenerowane) i zdegenerowane przekroje stożkowe można rozróżnić na podstawie wyznacznika A :

Jeśli ${\ displaystyle \ det A_ {Q} = 0}$ , stożek jest zdegenerowany.

Jeśli ${\ Displaystyle \ det A_ {Q} \ neq 0}$ tak, że Q nie jest zdegenerowany, możemy zobaczyć, jaki to jest typ przekroju stożkowego, obliczając mniejszy , det $\ Displaystyle \ det A_ { 33}}$ :

• Q jest hiperbolą wtedy i tylko wtedy, gdy ${\ displaystyle \ det A_ {33}<0}$ ,
• Q jest parabolą wtedy i tylko wtedy, gdy ${\ Displaystyle \ det A_ {33} = 0}$ i
• Q jest elipsą wtedy i tylko wtedy, gdy ${\ Displaystyle \ det A_ {33}> 0}$ .

W przypadku elipsy szczególny przypadek koła możemy wyróżnić porównując dwa ostatnie elementy diagonalne odpowiadające współczynnikom x ² i y ² :

• Jeśli A = C i B = 0 , to Q jest kołem.

Co więcej, w przypadku niezdegenerowanej elipsy (z ${\ Displaystyle \ det A_ {33}> 0}$ i ${\ Displaystyle \ det A_ {Q} \ neq 0}$ ) mieć prawdziwą elipsę, jeśli $Q}<0}$ ale wyimaginowaną elipsę, jeśli ${\ Displaystyle (A + C) \ det A_ {Q}> 0}$ . Przykładem tego ostatniego $ma$ rzeczywistych

Jeśli przekrój stożkowy jest zdegenerowany ( $A_ {Q} = 0}$$det$ ), pozwala nam rozróżnić jego

• Dwie przecinające się linie (hiperbola zdegenerowana do swoich dwóch asymptot) wtedy i tylko wtedy, gdy ${\ displaystyle \ det A_ {33}<0}$ .
• Dwie równoległe linie proste ( zdegenerowana parabola ) wtedy i tylko wtedy, gdy ${\ Displaystyle \ det A_ {33} = 0}$ . Linie te są różne i rzeczywiste, jeśli ${\ Displaystyle D ^ {2} + E ^ {2}> 4 (A + C) F}$ , zbieżne, jeśli ${\ Displaystyle D ^ {2} + E ^ {2} = 4 (A + C) F}$ i nie istnieje na płaszczyźnie rzeczywistej, jeśli ${\ Displaystyle D ^ {2} + E ^ {2}<4 (A + C) F}$ .
• Pojedynczy punkt (zdegenerowana elipsa) wtedy i tylko wtedy, gdy ${\ Displaystyle \ det A_ {33}> 0}$ .

Przypadek zbieżnych linii występuje wtedy i tylko wtedy, gdy ranga macierzy 3 × 3 ${\ displaystyle A_ {Q}}$ 1; ZA we wszystkich innych zdegenerowanych przypadkach jego ranga wynosi 2.

Stożki środkowe

Gdy istnieje geometryczny środek przekroju stożkowego i takie przekroje stożkowe (elipsy i hiperbole) nazywane są stożkami centralnymi ${\ Displaystyle \ det A_ {33} \ neq 0$ }

Centrum

Środek stożka, jeśli istnieje, jest punktem, który przecina wszystkie cięciwy stożka, które przez niego przechodzą. Tej właściwości można użyć do obliczenia współrzędnych środka, który można pokazać jako punkt, w którym gradient funkcji kwadratowej Q - to znaczy

${\ Displaystyle \ nabla Q = \ lewo [{\ Frac {\ częściowe Q} {\ częściowe x}}, {\ Frac {\ częściowe Q} {\ częściowe y}} \ prawej] = [0,0].}$

Daje to środek podany poniżej.

Alternatywne podejście wykorzystujące postać macierzową równania kwadratowego opiera się na fakcie, że gdy środek jest początkiem układu współrzędnych, w równaniu nie ma wyrazów liniowych. Dowolne przekształcenie na początek układu współrzędnych ₀₀ ( x , y ) przy użyciu x * = x – x ₀ , y * = y − y ₀ daje początek

${\ Displaystyle \ lewo ({\ rozpocząć {macierz} x ^ {*} + x_ {0} i y ^ {*} + y_ {0} \ koniec {macierz}} \ prawo) \ lewo ({\ rozpocząć {macierz} A&B/2\\B/2&C\end{macierz}}\right)\left({\begin{matrix}x^{*}+x_{0}\\y^{*}+y_{0}\end {macierz}}\right)+\left({\begin{matrix}D&E\end{matrix}}\right)\left({\begin{matrix}x^{*}+x_{0}\\y^ {*}+y_{0}\end{macierz}}\right)+F=0.}$

Warunkiem, aby ₀₀ ( x , y ) było środkiem stożka ( x _c , y _c ) jest to, że współczynniki liniowych wyrazów x* i y* , gdy to równanie jest mnożone, wynoszą zero. Ten warunek daje współrzędne środka:

${\ Displaystyle {\ rozpocząć {pmatrix} x_ {c} \\ y_ {c} \ koniec {pmatrix}} = {\ rozpocząć {pmatrix} A&B/2 \\ B/2&C \ koniec {pmatrix}} ^ {\! -1}{\begin{pmatrix}-D/2\\-E/2\end{pmatrix}}={\begin{pmatrix}(BE-2CD)/(4AC-B^{2})\\( DB-2AE)/(4AC-B^{2})\end{pmatrix}}.}$

To obliczenie można również wykonać, biorąc pierwsze dwa wiersze powiązanej macierzy A _Q , mnożąc każdy przez ( x , y , 1) ^⊤ i ustawiając oba iloczyny wewnętrzne na 0, otrzymując następujący układ:

${\ Displaystyle Ax + (B/2) y + D/2 = 0,}$

${ \displaystyle (B/2)x+Cy+E/2=0.}$

Daje to powyższy punkt środkowy.

W przypadku paraboli, czyli gdy 4 AC − B ² = 0 , nie ma środka, ponieważ powyższe mianowniki stają się zerowe (lub, interpretując rzutowo , środek znajduje się na linii w nieskończoności ).

Wyśrodkowane równanie macierzowe

Środkowy (nieparaboliczny) stożek ${\ Displaystyle Ax ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F =0}$ można przepisać w postaci wyśrodkowanej macierzy jako

${\ Displaystyle \ lewo ({\ rozpocząć {macierz} x-x_ {c }&y-y_{c}\end{macierz}}\right)\left({\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right)\left({\begin{matrix }x-x_{c}\\y-y_{c}\end{macierz}}\right)=K,}$

Gdzie

${\ Displaystyle K = {\ Frac {- \ det (A_ {Q})} {AC- (B/2) ^ {2}}} = {\ Frac {- \ det (A_ {Q})} {\ det(A_{33})}}.}$

Wtedy dla przypadku elipsy AC > ( B /2) ² , elipsa jest rzeczywista, jeśli znak K jest równy znakowi ( A + C ) (to jest znak każdego z A i C ), urojona, jeśli one mają przeciwne znaki i zdegenerowaną elipsę punktową, jeśli K = 0 . W przypadku hiperboli AC < ( B /2) ² hiperbola jest zdegenerowana wtedy i tylko wtedy, gdy K = 0 .

Standardowa forma centralnego stożka

Główne artykuły: Przekrój stożkowy § Formy standardowe we współrzędnych kartezjańskich i Przekrój stożkowy § Konwersja do postaci kanonicznej

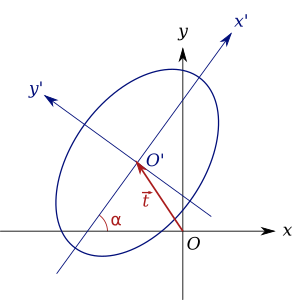
Standardową postać równania środkowego przekroju stożkowego uzyskuje się, gdy przekrój stożkowy jest przesuwany i obracany w taki sposób, że jego środek leży w środku układu współrzędnych, a jego osie pokrywają się z osiami współrzędnych. Jest to równoznaczne z powiedzeniem, że środek układu współrzędnych jest przesuwany, a osie współrzędnych są obracane, aby spełnić te właściwości. Na diagramie oryginalny xy z początkiem O został przeniesiony do układu współrzędnych x'y' z początkiem O' .

Przesuwanie i obracanie współrzędnych

Translacja odbywa się za pomocą wektora ${\ Displaystyle {\ vec {t}} = {\ rozpocząć {pmatrix} x_ {c} \\ y_ {c} \ koniec {pmatrix}}.}$

Obrót o kąt α można przeprowadzić przez diagonizację macierzy A ₃₃ . Zatem jeśli _i są $,$ własnymi macierzy A 33 równanie można przepisać na $zmienne$ x i y ' jako

${\ Displaystyle \ lambda _ {1} x' ^ {2} + \ lambda _ {2} y' ^ {2} = - {\ Frac {\ det A_ {Q}} {\ det A_ {33}}} .}$

Dzieląc przez $ZA$ otrzymujemy standardową postać

Na przykład dla elipsy ta forma jest

${\ Displaystyle {\ Frac {{x '} ^ {2}} {a ^ {2}}} + {\ Frac {{y'} ^ {2} }}{b^{2}}}=1.}$

Stąd otrzymujemy a i b , długości głównych i pół małych osi w notacji konwencjonalnej.

W przypadku stożków centralnych obie wartości własne są niezerowe, a klasyfikację przekrojów stożkowych można uzyskać, badając je.

• Jeśli λ ₁ i λ ₂ mają ten sam znak algebraiczny, to Q jest elipsą rzeczywistą, elipsą urojoną lub punktem rzeczywistym, jeśli K ma odpowiednio ten sam znak, przeciwny znak lub zero.
• Jeśli λ ₁ i λ ₂ mają przeciwne znaki algebraiczne, to Q jest hiperbolą lub dwiema przecinającymi się liniami, w zależności od tego, czy K jest odpowiednio niezerowe czy zerowe.

osie

Zgodnie z twierdzeniem o osi głównej dwa wektory własne macierzy formy kwadratowej centralnego przekroju stożka (elipsy lub hiperboli) są prostopadłe ( ortogonalne względem siebie) i każdy z nich jest równoległy (w tym samym kierunku co) do głównej lub mała oś stożka. Wektor własny o najmniejszej wartości własnej (w wartości bezwzględnej ) odpowiada głównej osi.

Konkretnie, jeśli środkowy przekrój stożkowy ma środek ( x _c , y _c ) i wektor własny A ₃₃ jest dany przez v → ( v ₁ , v ₂ ) , to główna oś (większa lub mniejsza) odpowiadająca temu wektorowi własnemu ma równanie:

${\ Displaystyle {\ Frac {xx_ {c}} {v_ {1}}} = {\ Frac {y-y_ {c}} {v_ {2}}}.}$

Wierzchołki

Wierzchołki stożka środkowego można wyznaczyć, obliczając przecięcia stożka i jego osi — innymi słowy, rozwiązując układ składający się z kwadratowego równania stożka i równania liniowego dla naprzemiennie jednej lub drugiej osi. Dla każdej osi uzyskuje się dwa wierzchołki lub nie uzyskuje się ich wcale, ponieważ w przypadku hiperboli oś mniejsza nie przecina hiperboli w punkcie o rzeczywistych współrzędnych. Jednak z szerszego spojrzenia na płaszczyznę zespoloną , mniejsza oś hiperboli przecina hiperbolę, ale w punktach o zespolonych współrzędnych.

Bieguny i bieguny

Główny artykuł: Polak i biegun

Korzystając z jednorodnych współrzędnych , punkty

${\ Displaystyle \ mathbf {p} = {\ rozpocząć {pmatrix} p_ {0} \\ p_ {1} \\ p_ {2} \ koniec {pmatrix}}}$ i ${\ Displaystyle \ mathbf {r} = {\ rozpocząć {pmatrix} r_ {0} \\ r_ {1} \\ r_ {2} \ koniec {pmatrix}}}$

są sprzężone w odniesieniu do dostarczonego stożkowego Q

${\ Displaystyle \ mathbf {p} ^ {T} A_ {Q} \ mathbf {r} = 0.}$

Koniugaty punktu stałego p albo tworzą linię, albo składają się ze wszystkich punktów na płaszczyźnie stożka. Kiedy koniugaty p tworzą linię, linię nazywamy biegunową p , a punkt p nazywamy biegunem linii, w odniesieniu do stożka. Ta zależność między punktami a liniami nazywana jest biegunowością .

Jeśli stożek nie jest zdegenerowany, koniugaty punktu zawsze tworzą linię, a biegunowość określona przez stożek jest bijekcją między punktami i liniami rozciągłej płaszczyzny zawierającej stożek (czyli płaszczyzny wraz z punktami i linia w nieskończoności ).

Jeśli punkt p leży na stożku Q , linia biegunowa p jest styczną do Q w punkcie p .

Równanie we współrzędnych jednorodnych linii biegunowej punktu p względem niezdegenerowanego stożka Q jest określone wzorem

${\ Displaystyle \ mathbf {p} ^ {T} A_ {Q} {\ początek {pmatrix} x \\ y \\ z \ koniec {pmatrix}} = 0. }$

Tak jak p jednoznacznie określa swoją linię biegunową (w odniesieniu do danego stożka), tak każda prosta określa unikalny biegun p . Ponadto punkt p leży na prostej L , która jest biegunem punktu r , wtedy i tylko wtedy, gdy biegun p przechodzi przez punkt r ( twierdzenie La Hire'a ). Zależność ta jest więc wyrazem geometrycznej dualności między punktami i prostymi na płaszczyźnie.

Kilka znanych koncepcji dotyczących przekrojów stożkowych jest bezpośrednio związanych z tą biegunowością. Środek niezdegenerowanego stożka można zidentyfikować jako biegun linii w nieskończoności . Parabola, będąc styczną do linii w nieskończoności, miałaby środek będący punktem na linii w nieskończoności. Hiperbole przecinają linię w nieskończoności w dwóch różnych punktach, a linie biegunowe tych punktów są asymptotami hiperboli i są liniami stycznymi do hiperboli w tych punktach nieskończoności. Również linia biegunowa ogniska stożka jest odpowiadającą mu kierownicą.

Styczne

Niech prosta L będzie linią biegunową punktu p względem niezdegenerowanego stożka Q . Zgodnie z twierdzeniem La Hire'a każda prosta przechodząca przez p ma swój biegun na L . Jeśli L przecina Q w dwóch punktach (maksimum możliwych), to bieguny tych punktów są liniami stycznymi przechodzącymi przez p i taki punkt nazywany jest zewnętrznym lub zewnętrznym punktem Q . Jeśli L przecina Q tylko w jednym punkcie, to jest to prosta styczna, a p jest punktem styczności. Wreszcie, jeśli L nie przecina Q , to p nie ma przechodzących przez nie linii stycznych i nazywa się to punktem wewnętrznym lub wewnętrznym .

Równanie linii stycznej (we współrzędnych jednorodnych) w punkcie p na niezdegenerowanym stożku Q jest określone wzorem

${\ Displaystyle \ mathbf {p} ^ {T} A_ {Q} {\ początek {pmatrix} x \\ y \\ z \ koniec {pmatrix}} = 0. }$

Jeśli p jest punktem zewnętrznym, najpierw znajdź równanie jego bieguna (powyższe równanie), a następnie przecięcia tej prostej ze stożkiem, powiedzmy w punktach s i t . Bieguny s i t będą stycznymi przechodzącymi przez p .

Korzystając z teorii biegunów i biegunów, problem znalezienia czterech wzajemnych stycznych dwóch stożków sprowadza się do znalezienia punktu przecięcia dwóch stożków .

Zobacz też

• Przekrój stożkowy # Ogólna forma kartezjańska
• Forma kwadratowa (statystyka)

Notatki

• Ayoub , AB ( 1993 ) _ _
•   Brannan, David A.; Esplen, Matthew F.; Szary, Jeremy J. (1999), Geometria , Cambridge University Press, ISBN 978-0-521-59787-6
• Lawrence, J. Dennis (1972), Katalog specjalnych krzywych płaszczyzny , Dover
•   Ostermann, Aleksander; Wanner, Gerhard (2012), Geometria według swojej historii , Springer, doi : 10.1007/978-3-642-29163-0 , ISBN 978-3-642-29163-0
•   Pettofrezzo, Anthony (1978) [1966], Matryce i transformacje , Dover, ISBN 978-0-486-63634-4
•   Hiszpania, Barry (2007) [1957], stożki analityczne , Dover, ISBN 978-0-486-45773-4