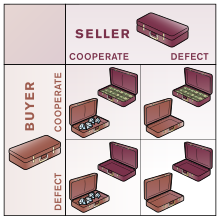
Dylemat więźnia

Standardowa macierz wypłat dylematu więźnia
B A	B milczy	B zdradza
A milczy	−2 −2	0 -10
Zdradza _	-10 0	−5 −5

Dylemat więźnia to gra analizowana w teorii gier ^{[ potrzebne źródło ]} . To eksperyment myślowy, który rzuca dwóm całkowicie racjonalnym agentom dylemat: mogą współpracować ze swoim partnerem dla obopólnych korzyści lub zdradzić partnera („wada”) dla indywidualnej nagrody.

Dylemat ten został pierwotnie sformułowany przez Merrilla Flooda i Melvina Dreshera w 1950 roku, kiedy pracowali w RAND ^{[ potrzebne źródło ]} . Albert W. Tucker sformalizował później grę, konstruując nagrody w kategoriach kar pozbawienia wolności i nazwał ją „dylematem więźnia”. William Poundstone opisał tę grę w swojej książce Prisoner's Dilemma z 1993 roku :

Dwóch członków gangu przestępczego A i B zostaje aresztowanych i uwięzionych. Każdy więzień przebywa w izolatce i nie ma możliwości komunikowania się ze swoim partnerem. Główny zarzut groziłby karą dziesięciu lat więzienia; jednakże policja nie ma dowodów pozwalających na wydanie wyroku skazującego. Planują skazać obu na dwa lata więzienia za mniejszą stawkę, ale oferują każdemu więźniowi faustowski układ : jeśli jeden z nich przyzna się do przestępstwa z głównego zarzutu, zdradzając drugiego, zostanie ułaskawiony i będzie mógł opuścić inny musi odbyć całą karę, a nie tylko dwa lata za niższy zarzut.

Prowadzi to do możliwych czterech różnych wyników:

Odpowiedź: Jeśli obaj A i B będą milczeć, każdemu z nich odsiedzi mniejszy zarzut, czyli 2 lata więzienia.
B: Jeśli A zdradzi B, ale B będzie milczeć, A zostanie uwolniony, a B odsiedzi 10 lat więzienia.
C: Jeśli A będzie milczeć, ale B zdradzi A, A odsiedzi 10 lat w więzieniu, a B zostanie uwolniony.
D: Jeżeli A i B zdradzą się nawzajem, podzielą się wyrokiem i odsiedzą 5 lat.

Dylemat więźnia, będący projekcją racjonalnego zachowania pod względem lojalności wobec partnera w przestępstwie, sugeruje, że przestępca, któremu zaoferuje się większą nagrodę, zdradzi swojego partnera.

Lojalność wobec partnera jest w tej grze irracjonalna. To szczególne założenie racjonalności implikuje, że jedynym możliwym rezultatem dla dwóch czysto racjonalnych więźniów jest zdrada, nawet jeśli wzajemna współpraca przyniosłaby większą nagrodę netto. Zaproponowano alternatywne koncepcje rządzące zachowaniem – zob. na przykład Elinor Ostrom .

Najlepsza odpowiedź, tj. dominującą strategią jest zdradzenie drugiego, co jest zgodne z zasadą pewności . Dylemat więźnia ilustruje również, że decyzje podejmowane w ramach racjonalności zbiorowej niekoniecznie muszą być takie same, jak te podejmowane w ramach racjonalności indywidualnej. Konflikt ten jest także widoczny w sytuacji zwanej „ Tragedia wspólnoty gmin ”.

W rzeczywistości systemowe nastawienie na zachowania oparte na współpracy ma miejsce pomimo przewidywań prostych modeli „racjonalnego” działania opartego na własnym interesie. To nastawienie na współpracę było widoczne od czasu, gdy tę grę po raz pierwszy przeprowadzono w RAND: zaangażowani sekretarze często ufali sobie nawzajem i pracowali razem, aby osiągnąć jak najlepszy wspólny wynik.

Dylemat więźnia stał się przedmiotem szeroko zakrojonych badań eksperymentalnych. Badania te przyjęły jedną z trzech form: grę pojedynczą (agenci grają tylko w jedną grę), grę iteracyjną (agenci grają w kilka gier z rzędu) i grę iteracyjną przeciwko zaprogramowanemu graczowi. Badania nad dylematem więźnia uzasadniły imperatyw kategoryczny podniesiony przez Immanuela Kanta , który stwierdza, że od racjonalnego podmiotu oczekuje się „działania w sposób, w jaki chciałbyś, aby inni postępowali”. Teoria ta jest niezbędna w sytuacji, w której biorą udział różni gracze, z których każdy działa w swoim najlepszym interesie, a którzy muszą wziąć pod uwagę działania innych, aby dokonać własnego wyboru.

W „iteracyjnym” wariancie gry, w którym dwóch agentów gra przeciwko sobie kilka razy, agenci w sposób ciągły mają możliwość ukarania drugiego za wcześniejsze decyzje. Jeśli gracze wiedzą, ile razy gra zostanie rozegrana, to poprzez indukcję wsteczną dwóch klasycznie racjonalnych graczy zdradzi się wielokrotnie, z tych samych powodów, co w wariancie jednostrzałowym. W grze o nieskończonej lub nieznanej długości nie ma ustalonej optymalnej strategii i organizuje się turnieje dylematu więźnia, aby rywalizować i testować algorytmy dla takich przypadków.

Szczególne zainteresowanie badaczy budzi iterowana wersja dylematu więźnia. Ze względu na iteracyjny charakter poprzednich badaczy zaobserwowali, że częstotliwość współpracy graczy może się zmieniać w zależności od wyników każdej iteracji. W szczególności gracz może być mniej chętny do współpracy, jeśli jego odpowiednik nie współpracował wiele razy, co powoduje rozczarowanie. I odwrotnie, z biegiem czasu współpraca może się nasilić w wyniku zawarcia „milczącego porozumienia” między graczami. Innym aspektem powtarzanej wersji eksperymentu jest to, że milczące porozumienie między graczami zawsze było osiągane z sukcesem, nawet jeśli liczba iteracji była podawana do wiadomości publicznej obu stronom.

Gra dylemat więźnia może modelować wiele rzeczywistych sytuacji obejmujących zachowania kooperacyjne. W codziennym użyciu etykietę „dylemat więźnia” można zastosować do każdej sytuacji, w której dwa podmioty mogłyby odnieść istotne korzyści ze współpracy lub ucierpieć z powodu jej zaniechania, ale koordynacja ich działań jest dla nich trudna lub kosztowna – choć niekoniecznie niemożliwa .

Strategia dylematu więźnia

Dwóch więźniów jest rozdzielonych do oddzielnych pomieszczeń i nie mogą się ze sobą komunikować. Poniżej pokazano normalną grę:

Więzień B Więzień A	Więzień B milczy ( współpracuje )	Więzień B zdradza ( wady )
Więzień A milczy ( współpracuje )	Każdy służy 2 lata	Więzień A: 10 lat Więzień B: wychodzi na wolność
Więzień A zdradza ( wady )	Więzień A: wychodzi na wolność Więzień B: 10 lat	Każdy służy 5 lat

Zakłada się, że obaj więźniowie rozumieją naturę gry, nie są wobec siebie lojalni i nie będą mieli możliwości zemsty ani nagrody poza grą. Niezależnie od decyzji drugiej strony, każdy więzień otrzymuje wyższą nagrodę za zdradę drugiego („ucieczka”). Rozumowanie obejmuje analizę najlepszych reakcji obu graczy : B albo będzie współpracował, albo odstąpi. Jeżeli B współpracuje, A powinien odejść, bo lepsze jest wyjście na wolność niż 2 lata więzienia. Jeśli B odsiaduje dezercję, A również powinien odejść, ponieważ odsiadywanie 5 lat jest lepsze niż 10 lat. Tak czy inaczej, A powinien odsiedzieć dezercję, ponieważ dezercja jest najlepszą reakcją A, niezależnie od strategii B. Równoległe rozumowanie pokaże, że B powinien zdezerterować.

Dezercja zawsze skutkuje lepszą wypłatą niż współpraca, dlatego jest to strategia ściśle dominująca zarówno dla A, jak i B. Wzajemna dezercja jest jedyną silną równowagą Nasha w grze (tzn. jedynym wynikiem, w którym każdy gracz może jednostronnie osiągnąć tylko gorsze wyniki). zmiana strategii). Dylemat polega na tym, że wzajemna współpraca daje lepszy wynik niż wzajemna zdrada, ale nie jest wynikiem racjonalnym, ponieważ decyzja o współpracy z punktu widzenia własnego interesu jest irracjonalna. Zatem dylemat więźnia jest grą, w której równowaga Nasha nie jest efektywna w sensie Pareto .

Uogólniona forma

Strukturę tradycyjnego dylematu więźnia można uogólnić na podstawie jego pierwotnego kontekstu więźnia. Załóżmy, że obaj gracze są reprezentowani przez kolory czerwony i niebieski i że każdy z nich wybiera albo „współpracę”, albo „wadę”.

Jeśli obaj gracze współpracują, obaj otrzymują nagrodę R za współpracę. Jeśli obaj gracze odejdą, obaj otrzymają karę P . Jeśli Niebieski złamie się, podczas gdy Czerwony będzie współpracował, wówczas Niebieski otrzyma pokusę T , podczas gdy Czerwony otrzyma nagrodę „frajera” S . Podobnie, jeśli Niebieski współpracuje, podczas gdy Czerwony odmawia, wówczas Niebieski otrzymuje zapłatę S od frajera , podczas gdy Czerwony otrzymuje zapłatę za pokusę T.

Można to wyrazić w postaci normalnej :

Kanoniczna macierz wypłat PD
Czerwony Niebieski	Współpracować	Wada
Współpracować	R R	T S
Wada	S T	P P

aby była to gra oparta na dylematach więźnia w mocnym tego słowa znaczeniu, w przypadku wypłat musi spełnić następujący warunek:

{\ displaystyle T> R> P> S}

Relacja wypłaty implikuje, że wzajemna współpraca jest lepsza od wzajemnej zdrady, podczas gdy relacje wypłat i ${\ displaystyle T> R}$ $oznaczają,$ R $> P}$ Dezercja jest dominującą strategią obu agentów.

Przypadek specjalny: gra polegająca na darowiznach

„Gra o darowizny” to forma dylematu więźnia, w której współpraca polega na zaoferowaniu drugiemu graczowi korzyści b po osobistym koszcie c , gdzie b > c . Dezercja oznacza nieoferowanie niczego. Macierz wypłat wygląda następująco

Czerwony Niebieski	Współpracować	Wada
Współpracować	b - do b - do	B - ok
Wada	- ok B	0 0

Należy zauważyć, że $displaystyle$ tj $2R> T + S} ($ grę w zakresie grę (patrz następna sekcja).

Gra w darowizny może zostać zastosowana na rynkach. Załóżmy, że X uprawia pomarańcze, a Y jabłka. Użyteczność krańcowa jabłka dla plantatora pomarańczy X wynosi b i jest wyższa niż użyteczność krańcowa ( c ) pomarańczy, ponieważ X ma nadwyżkę pomarańczy i nie ma jabłek. Podobnie dla hodowcy jabłek Y użyteczność krańcowa pomarańczy wynosi b , podczas gdy użyteczność krańcowa jabłka wynosi c . Jeśli X i Y zawrą umowę na wymianę jabłka i pomarańczy i każdy z nich wypełni swoją część umowy, wówczas każdy otrzyma wypłatę w wysokości b - c . Jeśli ktoś „wadzi” i nie dostarcza zgodnie z obietnicą, dezerter otrzyma zapłatę w wysokości b , podczas gdy współpracownik straci c . Jeśli obydwaj zawiodą, żaden z nich nic nie zyska ani nie straci.

Powtarzający się dylemat więźnia

Jeśli dwóch graczy rozegra dylemat więźnia więcej niż raz z rzędu, pamiętając poprzednie działania swojego przeciwnika i może odpowiednio zmienić swoją strategię, grę nazywa się iterowanym dylematem więźnia.

Oprócz powyższej ogólnej formy, wersja iteracyjna wymaga również, $zapobiec$ i dezercji, dającej większą nagrodę niż

Gra w powtarzalny dylemat więźnia ma fundamentalne znaczenie dla niektórych teorii ludzkiej współpracy i zaufania. Zakładając, że gra skutecznie modeluje transakcje między dwojgiem ludzi wymagające zaufania, zachowania kooperacyjne w populacjach można modelować za pomocą iterowanej wersji gry dla wielu graczy. W 1975 roku Grofman i Pool oszacowali liczbę poświęconych temu artykułom naukowym na ponad 2000. Powtarzający się dylemat więźnia nazywany jest także „ grą w wojnę pokojową ”.

Jeśli gra zostanie rozegrana N razy i obaj gracze o tym wiedzą, wówczas dominującą strategią jest dezercja we wszystkich rundach. Jedyną możliwą równowagą Nasha jest zawsze defekt. Dowód jest indukcyjny : równie dobrze można zdezerterować w ostatniej turze, ponieważ przeciwnik nie będzie miał szansy na późniejszy odwet. Dlatego obaj ulegną dezercji w ostatniej turze. Zatem gracz może równie dobrze zdezerterować w przedostatniej turze, ponieważ przeciwnik zdezerteruje w ostatniej turze, niezależnie od tego, co się stanie, i tak dalej. To samo dotyczy sytuacji, gdy długość gry jest nieznana, ale ma znany górny limit.

W przeciwieństwie do standardowego dylematu więźnia, w powtarzalnym dylemacie więźnia strategia ucieczki jest sprzeczna z intuicją i nie pozwala przewidzieć zachowania graczy-ludzi, mimo że dezercja jest jedyną poprawną odpowiedzią w standardowej teorii gier. Strategia superracjonalna w iterowanym dylemacie więźnia z ustalonym N polega na współpracy przeciwko ponadracjonalnemu przeciwnikowi, a w granicach dużego N wyniki eksperymentów dotyczące strategii są zbieżne z wersją superracjonalną, a nie racjonalną z teorii gier.

Aby między racjonalnymi graczami zajmującymi się teorią gier mogła zaistnieć współpraca , liczba rund N musi być nieznana graczom. W tym przypadku „zawsze defekt” może nie być już strategią ściśle dominującą, ale jedynie równowagą Nasha. Jak pokazał Robert Aumann w artykule z 1959 r., ^{[ potrzebne źródło ]} racjonalni gracze, którzy wielokrotnie wchodzą w interakcje w nieskończenie długich grach, mogą podtrzymać wynik współpracy.

Według eksperymentalnego badania przeprowadzonego w 2019 r. w American Economic Review, w ramach którego sprawdzano, jakie strategie stosują prawdziwi badani w powtarzających się sytuacjach dylematu więźnia, przy doskonałym monitorowaniu, większość wybranych strategii zawsze polegała na ucieczce, wet za wet i ponurym wyzwalaczu . To, jaką strategię wybrali badani, zależało od parametrów gry.

Strategia dla iteracyjnego dylematu więźnia

Zainteresowanie iterowanym dylematem więźnia (IPD) rozbudził Robert Axelrod w swojej książce The Evolution of Cooperative (1984), w której relacjonuje zorganizowany przez siebie turniej dylematu więźnia stopnia N (wraz z N ustalone), w którym uczestnicy muszą raz po raz wybierać wspólną strategię i pamiętać swoje poprzednie spotkania. Axelrod zaprosił kolegów akademickich z całego świata do opracowania strategii komputerowych umożliwiających rywalizację w turnieju IPD. Programy, które wprowadzono, różniły się znacznie pod względem złożoności algorytmicznej, początkowej wrogości, zdolności do przebaczenia i tak dalej.

Axelrod odkrył, że kiedy te spotkania powtarzały się przez długi czas z wieloma graczami, każdy z inną strategią, strategie zachłanne na dłuższą metę radziły sobie bardzo słabo, podczas gdy strategie bardziej altruistyczne radziły sobie lepiej, oceniając wyłącznie na podstawie własnego interesu . Wykorzystał to, aby pokazać możliwy mechanizm ewolucji zachowań altruistycznych z mechanizmów, które początkowo są czysto egoistyczne, w drodze doboru naturalnego .

Zwycięską strategią deterministyczną była „wet za wet” , opracowana i wprowadzona do turnieju przez Anatola Rapoporta . Był to najprostszy ze wszystkich wprowadzonych programów, zawierający tylko cztery linie języka BASIC i wygrał konkurs. Strategia polega po prostu na współpracy przy pierwszej iteracji gry; następnie gracz robi to samo, co zrobił jego przeciwnik w poprzednim ruchu. W zależności od sytuacji nieco lepszą strategią może być „wet za wet z przebaczeniem”. Kiedy przeciwnik dezerteruje, w następnym ruchu gracz czasami i tak współpracuje z małym prawdopodobieństwem (ok. 1–5%). Pozwala to na okazjonalne wyzdrowienie z uwięzienia w cyklu dezercji. Dokładne prawdopodobieństwo zależy od składu przeciwników.

Po przeanalizowaniu strategii zapewniających najwyższe wyniki Axelrod stwierdził kilka warunków niezbędnych, aby strategia odniosła sukces:

Ładna: Najważniejszym warunkiem jest to, że strategia musi być „ładna”. Oznacza to, że nie ulegnie defektowi, zanim zrobi to jego przeciwnik (czasami nazywa się to algorytmem „optymistycznym”). Prawie wszystkie strategie zapewniające najwyższą liczbę punktów były dobre. Strategia czysto egoistyczna nie „oszuka” przeciwnika najpierw z powodów czysto egoistycznych.
Odwet: Axelrod twierdził jednak, że skuteczna strategia nie może być ślepym optymistą; czasami musi wziąć odwet. Przykładem strategii braku odwetu jest Always Corate, bardzo zły wybór, który będzie często wykorzystywany przez „paskudne” strategie.
Przebaczanie: Skuteczne strategie muszą także polegać na przebaczaniu. Chociaż gracze zemszczą się, ponownie powrócą do współpracy, jeśli przeciwnik nie będzie nadal uciekał. Może to zatrzymać długie serie zemsty i przeciwrewanżu, maksymalizując punkty.
Brak zawiści: Ostatnią cechą jest brak zawiści, co oznacza, że nie starasz się zdobyć więcej punktów niż przeciwnik.

Optymalną strategią (maksymalizującą punkty) w jednorazowej grze PD jest po prostu dezercja; jak wyjaśniono powyżej, jest to prawdą niezależnie od składu przeciwników (zwanych łącznie „populacją”). Jednak w grze iterowanej PD optymalna strategia zależy od strategii prawdopodobnych przeciwników oraz ich reakcji na dezercje i współpracę. Rozważmy na przykład populację, w której wszyscy za każdym razem dezerterują, z wyjątkiem jednej osoby stosującej strategię „wet za wet”. Osoba ta jest w nieco gorszej sytuacji z powodu porażki w pierwszej turze. W takiej populacji optymalną strategią dla tej osoby jest dezercja za każdym razem. Z kolei, biorąc pod uwagę populację z pewnym odsetkiem zawsze dezerterów, a reszta to gracze typu „wet za wet”, optymalna strategia dla danej osoby zależy od odsetka i ilości rozegranych iteracji.

W strategii zwanej Pavlov, wygrana-zostań, przegrana-zmiana , w obliczu braku współpracy, gracz zmienia strategię w następnej turze. W pewnych okolicznościach ^{[ określ ]} Pawłow przewyższa wszystkie inne strategie, preferencyjnie traktując współgraczy stosujących podobną strategię.

Wyznaczanie optymalnej strategii odbywa się zazwyczaj na dwa sposoby:

Równowaga Bayesa Nasha : Jeśli można określić statystyczny rozkład przeciwstawnych strategii (np. 50% wet za wet, 50% zawsze współpracuje), można analitycznie wyprowadzić optymalną przeciwstrategię.
Przeprowadzono symulacje Monte Carlo populacji, w których osobniki z niskimi wynikami wymierają, a te z wysokimi wynikami rozmnażają się ( algorytm genetyczny pozwalający znaleźć optymalną strategię). Mieszanka algorytmów w populacji końcowej generalnie zależy od kombinacji w populacji początkowej. Wprowadzenie mutacji (losowej zmienności podczas reprodukcji) zmniejsza zależność od populacji początkowej; eksperymenty empiryczne z takimi systemami zwykle dają korzyści graczom (patrz na przykład Chess 1988), ^{[ potrzebne wyjaśnienie ]} , ale nie istnieje żaden analityczny dowód, że tak będzie zawsze.

Chociaż „wet za wet” jest uważany za najsolidniejszą strategię podstawową, zespół z Uniwersytetu w Southampton w Anglii wprowadziło nową strategię podczas konkursu iterowanych dylematów więźnia z okazji 20. rocznicy, która okazała się skuteczniejsza niż wet za wet. Strategia ta opierała się na zmowie między programami w celu uzyskania jak największej liczby punktów dla pojedynczego programu. Uczelnia zgłosiła do konkursu 60 programów, które miały na celu wzajemne rozpoznanie się na starcie poprzez serię od pięciu do dziesięciu ruchów. Po dokonaniu tego rozpoznania jeden program zawsze współpracował, a drugi zawsze dezerterował, zapewniając dezerterowi maksymalną liczbę punktów. Gdyby program zdał sobie sprawę, że gra z graczem spoza Southampton, stale dezerterowałby, próbując zminimalizować wynik konkurencyjnego programu. W rezultacie widać wyniki Turnieju Dylematów Więźniów z 2004 roku Uniwersytetu w Southampton na pierwszych trzech miejscach (i kilka pozycji w dół), pomimo mniejszej liczby zwycięstw i znacznie większej liczby porażek niż strategia GRIM. (W turnieju PD celem gry nie jest „wygrywanie” meczów – co można łatwo osiągnąć poprzez częste ucieczki).

Strategia z Southampton wykorzystuje fakt, że w tych konkretnych rozgrywkach dopuszczono wiele zgłoszeń i że wyniki drużyny mierzono na podstawie wyników gracza, który zdobył najwięcej punktów (co oznacza, że wykorzystanie poświęcających się graczy było formą minmaxingu ) . . Ze względu na tę nową zasadę zawody te mają również niewielkie znaczenie teoretyczne przy analizie strategii pojedynczego agenta w porównaniu z przełomowym turniejem Axelroda. Zapewniło to jednak podstawę do analizy, w jaki sposób można osiągnąć strategie współpracy w środowiskach wieloagentowych, szczególnie w obecności szumu. Dawkins w swojej książce tak naprawdę na długo przed rozegraniem tego turnieju według nowych zasad Samolubny gen wskazał na możliwość wygrania takich strategii, gdyby pozwolono na wielokrotne zgłoszenia, ale zauważył, że najprawdopodobniej Axelrod by na nie nie pozwolił, gdyby zostały zgłoszone. Opiera się również na obchodzeniu przepisów dotyczących dylematu więźnia, ponieważ między dwoma graczami nie jest dozwolona komunikacja, co prawdopodobnie zrobiły programy z Southampton dzięki zaprogramowanemu „taniecowi w dziesięciu ruchach”, aby się rozpoznawać; podkreślając, jak cenna może być komunikacja w zmianie równowagi gry.

Nawet bez ukrytej zmowy pomiędzy strategiami oprogramowania (wykorzystywanymi przez zespół z Southampton) „wet za wet” nie zawsze jest absolutnym zwycięzcą danego turnieju; precyzyjniej byłoby powiedzieć, że jej długoterminowe wyniki w serii turniejów przewyższają rywali. (W każdym przypadku dana strategia może być nieco lepiej dostosowana do konkurencji niż „wet za wet”, ale „wet za wet” jest solidniejsza). To samo dotyczy wariantu „wet za wet” z przebaczeniem i innych optymalnych strategii: w danym dniu mogą nie „wygrać” z określoną kombinacją strategii kontr. Alternatywnym sposobem wyrażenia tego jest użycie teorii darwinowskiej Symulacja ESS . W takiej symulacji zasada „wet za wet” prawie zawsze będzie dominować, chociaż paskudne strategie będą pojawiać się i wychodzić z populacji, ponieważ populację „wet za wet” można przeniknąć za pomocą miłych strategii niemających odwetu, które z kolei są łatwym łupem dla paskudnych. strategie. Richard Dawkins pokazał, że w tym przypadku żadna statyczna mieszanka strategii nie tworzy stabilnej równowagi, a system zawsze będzie oscylował pomiędzy granicami.

Stochastyczny iterowany dylemat więźnia

W stochastycznej grze z iterowanym dylematem więźnia strategie są określone w kategoriach „prawdopodobieństwa współpracy”. W spotkaniu pomiędzy graczem X i graczem Y , strategia X jest określona przez zbiór prawdopodobieństw P współpracy z Y. P jest funkcją wyników ich poprzednich spotkań lub ich podzbioru. Jeśli P jest funkcją tylko ich najnowszego n spotkania, nazywa się to strategią „pamięci-n”. Strategia pamięci-1 jest następnie określona przez cztery prawdopodobieństwa współpracy: ${dd} \}}$ ${\ Displaystyle P = \ {P_ {cc}, P_ {cd}, P_ {$ $jest$ , gdzie prawdopodobieństwo, że X będzie współpracować w obecnym spotkaniu, biorąc pod uwagę, że poprzednie spotkanie charakteryzowało się (ab). Na przykład, jeśli podczas poprzedniego spotkania X współpracował, a Y uciekł $,$ wówczas jest prawdopodobieństwo, że będzie obecnego spotkania. Jeśli każde z prawdopodobieństw wynosi 1 lub 0, strategię nazywa się deterministyczną. Przykładem strategii deterministycznej jest strategia „wet za wet” zapisana jako P ={1,0,1,0}, w której X odpowiada Y zrobił podczas poprzedniego spotkania. Inną jest wygrana – pozostanie, przegrana – zmiana zapisana jako P ={1,0,0,1}, w której X reaguje tak jak w poprzednim spotkaniu, jeśli była to „wygrana” (tj. zmienia strategię, jeśli była to strata (tj. cd lub dd). Wykazano, że dla każdej strategii pamięci-n istnieje odpowiadająca strategia pamięci-1, która daje takie same wyniki statystyczne, więc należy wziąć pod uwagę tylko strategie pamięci-1.

Jeśli zdefiniujemy P jako powyższy 4-elementowy wektor strategii X i ${\ displaystyle Q = \ {Q_ {cc}, Q_ {cd} ,Q_{dc},Q_{dd}\}}$ jako 4-elementowy wektor strategii Y , dla X można zdefiniować macierz przejścia M , której ij ten wpis to prawdopodobieństwo, że wynikiem konkretnego spotkania pomiędzy X i Y będzie j , biorąc pod uwagę, że poprzednim spotkaniem było i , gdzie i i j to jeden z czterech wskaźników wyniku: cc , cd , dc lub dd . Na przykład, z punktu widzenia X , prawdopodobieństwo, że wynik obecnego spotkania będzie cd , biorąc pod uwagę, że poprzednie spotkanie było cd jest równe ${\ Displaystyle M_ {cd, cd} = P_ {cd} (1-Q_ {dc})}$ . (Wskaźniki Q są z punktu widzenia Y : wynik cd dla X jest wynikiem DC dla Y. ) Zgodnie z tymi definicjami, iterowany dylemat więźnia kwalifikuje się jako proces stochastyczny i M jest macierzą stochastyczną , pozwalającą na zastosowanie całej teorii procesów stochastycznych.

Jednym z wyników teorii stochastycznej jest to, że istnieje stacjonarny wektor v dla macierzy M taki, że ${\ displaystyle v \ cdot M = v}$ . Bez utraty ogólności można określić, że v jest znormalizowane w taki sposób, że suma jego czterech składników wynosi jedność. Ij - $X$ wpis w poda prawdopodobieństwo , że wynikiem spotkania pomiędzy i Y j biorąc pod uwagę, że spotkanie z n kroków poprzedzających to i . W granicy, gdy n zbliża się do nieskończoności, M zbiegnie się do macierzy o ustalonych wartościach, dając długoterminowe prawdopodobieństwa spotkania dającego j , które będzie niezależne od i . Innymi słowy, wiersze będą identyczne, co da prawdopodobieństwa wyniku długoterminowej równowagi iterowanego dylematu więźnia bez konieczności jawnej oceny dużej $.$ Można zauważyć, że v jest wektorem stacjonarnym dla, $}$ $zwłaszcza dla$ , tak każdy wiersz $}$ być równy v . Zatem wektor stacjonarny określa prawdopodobieństwa wyniku równowagi dla X . Definiowanie i $S, T, P \}}$ , ${\ Displaystyle S_ {y} = \ {R, T, S, P \}}$ jako krótkoterminowe wektory wypłat dla {cc, cd, dc, dd} wyników (z punktu widzenia X ) wypłaty równowagi dla X i Y można teraz określić jako i ${\ displaystyle s_ {x} = v \ cdot S_$ { $umożliwiając porównanie$ dwóch strategii P i Q pod kątem ich długoterminowych korzyści.

Strategie o zerowej determinacji

Zależność między wyznacznikiem zerowym (ZD), strategiami współpracy i dezercji w iterowanym dylemacie więźnia (IPD) zilustrowanym na diagramie Venna . Strategie współpracujące zawsze współdziałają z innymi strategiami współpracującymi, a strategie dezercji zawsze ustępują innym strategiom dezercji. Obydwa zawierają podzbiory strategii, które są odporne w warunkach silnej selekcji, co oznacza, że żadna inna strategia pamięci-1 nie jest wybierana w celu inwazji na takie strategie, gdy są one obecne w populacji. Jedynie strategie współpracujące zawierają podzbiór, który jest zawsze solidny, co oznacza, że nie wybrano żadnej innej strategii pamięci-1, która mogłaby zaatakować i zastąpić takie strategie, zarówno w przypadku silnych, jak i słaby wybór . Punktem przecięcia ZD i dobrych strategii współpracujących jest zbiór hojnych strategii ZD. Strategie wymuszenia są skrzyżowaniem ZD i niesolidnych strategii dezercji. Wet za wet leży na skrzyżowaniu strategii współpracy, dezercji i ZD.

W 2012 roku William H. Press i Freeman Dyson opublikowali nową klasę strategii stochastycznego iterowanego dylematu więźnia, zwaną strategiami „zero determinanty” (ZD). Długoterminowe wypłaty w przypadku spotkań pomiędzy X i Y można wyrazić jako wyznacznik macierzy będącej funkcją obu strategii i krótkoterminowych wektorów wypłat: ${\ displaystyle s_ {x}=D(P,Q,S_{x})}$ i ${\ Displaystyle s_ {y} = D (P, Q, S_ {y})}$ , które nie obejmują stacjonarnego wektora v . Ponieważ funkcja wyznacznika w f , wynika z tego, że $\ Displaystyle s_ {y} = D (P$ ${\ Displaystyle \ alfa s_ {x} + \ beta s_ {y} + \ gamma = D (P, Q, \ alfa S_ {x} +\beta S_{y}+\gamma U)}$ (gdzie U = {1, 1, 1, 1} ). Dowolne strategie, dla których ${\ Displaystyle D (P, Q, \ alfa S_ {x} + \ beta S_ {y} + \ gamma U) = 0} jest$ z definicji strategią ZD, a długoterminowe korzyści są zgodne z zależnością ${\ displaystyle \ alfa s_ {x} + \ beta s_ {y} + \ gamma = 0}$ .

Wet za wet to strategia ZD, która jest „sprawiedliwa” w tym sensie, że nie polega na zdobywaniu przewagi nad drugim graczem. Jednak przestrzeń ZD zawiera również strategie, które w przypadku dwóch graczy mogą pozwolić jednemu z graczy jednostronnie ustalić wynik drugiego gracza lub alternatywnie zmusić gracza ewolucyjnego do osiągnięcia wypłaty o pewien procent niższej od jego własnej. Wymuszony gracz mógłby odejść, ale w ten sposób wyrządziłby sobie krzywdę, uzyskując niższą wypłatę. W ten sposób rozwiązania w zakresie wymuszenia zamieniają powtarzający się dylemat więźnia w rodzaj gry w ultimatum . W szczególności X jest w stanie wybrać strategię, dla której ${\ Displaystyle D (P, Q, \ beta S_ {y} + \ gamma U) = 0}$ , jednostronnie ustawiając $s_ {y}}$ displaystyle określona wartość w określonym zakresie wartości, niezależna od strategii Y , oferująca X możliwość „wymuszenia” gracza Y (i odwrotnie) . (Okazuje się, że jeśli X spróbuje ustawić $określonej$ wartości zakres możliwości jest znacznie mniejszy i obejmuje jedynie pełną współpracę lub całkowitą dezercję.)

Rozszerzeniem IPD jest ewolucyjna stochastyczna IPD, w której względna liczebność poszczególnych strategii może się zmieniać, przy stosunkowo większym wzroście skuteczniejszych strategii. Proces ten można osiągnąć poprzez naśladowanie przez mniej skutecznych graczy bardziej skutecznych strategii lub poprzez eliminację mniej skutecznych graczy z gry i pomnożenie tych, którzy odnieśli większy sukces. Wykazano, że nieuczciwe strategie ZD nie są ewolucyjnie stabilne . Kluczową intuicją jest to, że ewolucyjnie stabilna strategia musi nie tylko być w stanie zaatakować inną populację (co mogą zrobić wymuszenia strategii ZD), ale musi także dobrze radzić sobie z innymi graczami tego samego typu (co wyłudzający gracze ZD radzą sobie słabo, ponieważ zmniejszają wzajemne nadwyżka).

Teoria i symulacje potwierdzają, że powyżej krytycznej wielkości populacji wymuszenie ZD przegrywa w ewolucyjnej konkurencji ze strategiami bardziej kooperacyjnymi, w wyniku czego średnia wypłata w populacji wzrasta, gdy populacja jest większa. Ponadto w niektórych przypadkach oszuści mogą nawet katalizować współpracę, pomagając w przełamaniu starcia między uciekinierami w mundurach a agentami, w których wygrywa – zostaje, traci – zmienia .

Chociaż wymuszone strategie ZD nie są stabilne w dużych populacjach, inna klasa ZD, zwana strategiami „hojnymi”, jest zarówno stabilna, jak i solidna. W rzeczywistości, jeśli populacja nie jest zbyt mała, strategie te mogą zastąpić każdą inną strategię ZD, a nawet dobrze działać w porównaniu z szeroką gamą ogólnych strategii w przypadku powtarzającego się dylematu więźnia, w tym wygrana – pozostanie, przegrana – zmiana. Zostało to udowodnione szczególnie w przypadku gry w darowizny Aleksandra Stewarta i Joshuy Plotkina w 2013 roku. Strategie hojne będą współpracować z innymi graczami współpracującymi, a w obliczu dezercji hojny gracz traci więcej użyteczności niż jego rywal. Strategie hojne to skrzyżowanie strategii ZD i tak zwanych strategii „dobrych”, które Akin (2013) zdefiniował jako takie, w przypadku których gracz reaguje na przeszłą wzajemną współpracę z przyszłą współpracą i równo dzieli oczekiwane wypłaty, jeśli otrzyma co najmniej spółdzielnia oczekiwała wypłaty. Wśród dobrych strategii podzbiór hojny (ZD) sprawdza się dobrze, gdy populacja nie jest zbyt mała. Jeśli populacja jest bardzo mała, dominują strategie ucieczki.

Ciągły, powtarzający się dylemat więźnia

Większość prac nad iterowanym dylematem więźnia skupiała się na dyskretnym przypadku, w którym gracze albo współpracują, albo dezerterują, ponieważ model ten jest stosunkowo prosty do analizy. Jednak niektórzy badacze przyjrzeli się modelom ciągłego, iteracyjnego dylematu więźnia, w którym gracze mogą wnieść zmienny wkład na rzecz drugiego gracza. Le i Boyd odkryli, że w takich sytuacjach o wiele trudniej jest rozwinąć współpracę niż w przypadku dyskretnego, iterowanego dylematu więźnia. Podstawowa intuicja prowadząca do tego wyniku jest prosta: w przypadku dylematu ciągłego więźnia, jeśli populacja zaczyna od stanu równowagi braku współpracy, gracze, którzy są tylko nieznacznie bardziej skłonni do współpracy niż niewspółpracujący, odnoszą niewielkie korzyści z mieszając ze sobą. Z drugiej strony, w przypadku dyskretnego dylematu więźnia, współpracownicy „wet za wet” czerpią duży zastrzyk korzyści z dobierania się między sobą w równowadze niewspółpracującej w porównaniu z osobami niewspółpracującymi. Ponieważ natura prawdopodobnie oferuje więcej możliwości zmiennej współpracy niż ścisłą dychotomię współpracy lub ucieczki, ciągły dylemat więźnia może pomóc wyjaśnić, dlaczego rzeczywiste przykłady współpracy na zasadzie wet za wet są w przyrodzie niezwykle rzadkie (np. Hammerstein) chociaż wet za wet wydaje się solidny w modelach teoretycznych.

Pojawienie się stabilnych strategii

Wydaje się, że gracze nie są w stanie koordynować wzajemnej współpracy, dlatego często wpadają w gorszą, ale stabilną strategię dezercji. W ten sposób iterowane rundy ułatwiają ewolucję stabilnych strategii. Powtarzane rundy często prowadzą do powstania nowych strategii, które mają wpływ na złożone interakcje społeczne. Jedną z takich strategii jest wygrana – pozostanie – przegrana. Ta strategia przewyższa prostą strategię „wet za wet” – to znaczy, jeśli możesz uniknąć oszukiwania, powtórz to zachowanie. Jeśli jednak zostaniesz złapany, zmień.

Jedynym problemem tej strategii „wet za wet” jest to, że są one podatne na błędy sygnału. Problem pojawia się, gdy jedna osoba oszukuje w odwecie, a druga interpretuje to jako oszustwo. W rezultacie druga osoba oszukuje, a następnie rozpoczyna się huśtawkowy wzór oszukiwania w reakcji łańcuchowej.

Nawet bez powtarzających się gier silny, oświecony interes własny może skutkować stabilnym i skutecznym wynikiem.

Przykłady z życia

Sytuacja więźnia może wydawać się wymyślona, ale w rzeczywistości istnieje wiele przykładów interakcji międzyludzkich, a także interakcji w przyrodzie, które mają tę samą matrycę wypłat. Dylemat więźnia jest zatem przedmiotem zainteresowania nauk społecznych , takich jak ekonomia , polityka i socjologia , a także nauk biologicznych, takich jak etologia i biologia ewolucyjna . Wiele naturalnych procesów ujęto w modele, w których żywe istoty angażują się w niekończące się gry dylematem więźnia. To szerokie zastosowanie PD nadaje grze istotne znaczenie.

Badania środowiskowe

W badaniach środowiskowych PD jest widoczne w przypadku kryzysów takich jak globalna zmiana klimatu . Argumentuje się, że wszystkie kraje odniosą korzyści ze stabilnego klimatu, lecz żaden kraj często waha się przed ograniczeniem CO ₂ . Uważa się, że bezpośrednie korzyści dla dowolnego kraju z utrzymania obecnego zachowania będą większe niż rzekome ostateczne korzyści dla tego kraju w przypadku zmiany zachowania wszystkich krajów, co wyjaśnia impas dotyczący zmian klimatycznych w 2007 r.

Ważną różnicą między polityką dotyczącą zmian klimatycznych a dylematem więźnia jest niepewność; nie jest znany zakres i tempo, w jakim zanieczyszczenia mogą zmieniać klimat. Dylemat, przed którym stoją rządy, różni się zatem od dylematu więźnia tym, że korzyści ze współpracy są nieznane. Ta różnica sugeruje, że państwa będą współpracować znacznie mniej niż w przypadku rzeczywistego iterowanego dylematu więźnia, zatem prawdopodobieństwo uniknięcia ewentualnej katastrofy klimatycznej jest znacznie mniejsze niż to, które sugeruje analiza sytuacji oparta na teorii gier z wykorzystaniem prawdziwego iterowanego dylematu więźnia.

Osang i Nandy (2003) dostarczają teoretycznego wyjaśnienia wraz z dowodami na napędzaną regulacjami sytuację, w której wygrywają obie strony, zgodnie z hipotezą Michaela Portera , w której regulacja rządowa konkurujących firm jest znacząca.

Zwierząt

Jako przykład dylematu więźnia można rozumieć kooperatywne zachowanie wielu zwierząt. Często zwierzęta angażują się w długoterminowe partnerstwa, co można dokładniej modelować jako powtarzalny dylemat więźnia. Na przykład gupiki kontrolują drapieżniki wspólnie w grupach i uważa się, że karzą inspektorów odmawiających współpracy.

Nietoperze wampiry to zwierzęta społeczne, które angażują się w wzajemną wymianę pożywienia. Zastosowanie korzyści wynikających z dylematu więźnia może pomóc w wyjaśnieniu tego zachowania:

Współpracuj/Współpracuj: „Nagroda: dostaję krew w moje pechowe noce, co ratuje mnie przed śmiercią z głodu. Muszę oddawać krew w moje szczęśliwe noce, co nie kosztuje mnie zbyt wiele”.
Wada/Współpraca: „Pokusa: ratujesz mi życie podczas mojej kiepskiej nocy. Ale z drugiej strony otrzymuję dodatkową korzyść w postaci braku konieczności ponoszenia niewielkich kosztów karmienia cię podczas mojej dobrej nocy”.
Współpraca/Defekt: „Zapłata frajera: w moją dobrą noc płacę koszt ratowania twojego życia. Ale w moją złą noc nie nakarmisz mnie i ryzykuję, że umrę z głodu”.
Wada/wada: „Kara: nie muszę płacić niewielkich kosztów karmienia cię podczas moich dobrych nocy. Ale w czasie moich kiepskich nocy istnieje realne ryzyko, że umrę z głodu”.

Psychologia

W badaniach nad uzależnieniami / ekonomią behawioralną George Ainslie wskazuje, że uzależnienie można postrzegać jako międzyokresowy problem choroby Parkinsona, występujący pomiędzy teraźniejszością i przyszłą jaźnią osoby uzależnionej . W tym przypadku dezercja oznacza nawrót i łatwo zauważyć, że zaniechanie dezercji zarówno dzisiaj, jak i w przyszłości, jest zdecydowanie najlepszym rezultatem. Najgorszy wynik to sytuacja, w której ktoś powstrzymuje się od palenia dzisiaj, ale w przyszłości powróci do nałogu – w pewnym sensie dyscyplina i poświęcenie związane z dzisiejszą abstynencją zostały „zmarnowane”, ponieważ przyszły nawrót oznacza, że osoba uzależniona wróciła tam, gdzie zaczęła i będzie trzeba zaczynać od nowa (co jest dość demoralizujące i utrudnia rozpoczynanie od nowa). Nawrót do nałogu dzisiaj i jutro to nieco „lepszy” wynik, ponieważ osoba uzależniona nadal jest uzależniona, ale nie włożyła wysiłku w to, by przestać. Ostatni przypadek, w którym dzisiaj podejmuje się uzależniające zachowanie, a „jutro” powstrzymuje się od nałogu, będzie znany każdemu, kto zmagał się z nałogiem. Problem polega na tym, że (podobnie jak w przypadku innych PD) dezercja „dziś” przynosi oczywistą korzyść, ale jutro ktoś stanie w obliczu tego samego PD i wówczas pojawią się te same oczywiste korzyści, co ostatecznie doprowadzi do niekończącego się ciągu dezercji.

John Gottman w swoich badaniach opisanych w „The Science of Trust” definiuje dobre relacje jako takie, w których partnerzy wiedzą, aby nie wchodzić do komórki (D,D) lub przynajmniej nie wpadać w nią dynamicznie w pętlę. W neurobiologii poznawczej szybka sygnalizacja mózgowa związana z przetwarzaniem różnych rund może wskazywać na wybory w następnej rundzie. Wzajemne wyniki współpracy pociągają za sobą zmiany w aktywności mózgu, które pozwalają przewidzieć, jak szybko dana osoba będzie współpracować w naturze przy następnej okazji; aktywność ta może być powiązana z podstawowymi procesami homeostatycznymi i motywacyjnymi, prawdopodobnie zwiększając prawdopodobieństwo przejścia na skróty do komórki (C, C) gry.

Ekonomia

Dylemat więźnia został nazwany bakterią coli psychologii społecznej i był szeroko stosowany w badaniach nad różnymi tematami, takimi jak konkurencja oligopolistyczna i zbiorowe działania na rzecz wytworzenia dobra zbiorowego.

Reklama jest czasami przytaczana jako prawdziwy przykład dylematu więźnia. Kiedy reklama papierosów była legalna w Stanach Zjednoczonych, konkurujący producenci papierosów musieli decydować, ile pieniędzy wydać na reklamę. Skuteczność reklamy firmy A była częściowo zdeterminowana reklamą prowadzoną przez firmę B. Podobnie na zysk uzyskany z reklamy firmy B wpływa reklama prowadzona przez firmę A. Jeśli zarówno firma A, jak i firma B zdecydowały się reklamować w danym okresie, wówczas reklama jednej firmy neguje reklamę drugiej, wpływy pozostają stałe, a wydatki rosną ze względu na koszty reklamy. Obie firmy skorzystałyby na ograniczeniu reklam. Jeśli jednak firma B zdecyduje się nie reklamować, firma A może odnieść ogromne korzyści z reklamy. Niemniej jednak optymalna ilość reklam jednej firmy zależy od tego, ile reklam podejmie się druga. Ponieważ najlepsza strategia zależy od tego, co wybierze druga firma, nie ma strategii dominującej, co nieco różni się od dylematu więźnia. Wynik jest jednak podobny, ponieważ obie firmy byłyby w lepszej sytuacji, gdyby reklamowały się rzadziej niż w równowadze. Czasami w sytuacjach biznesowych pojawiają się zachowania oparte na współpracy. Na przykład producenci papierosów poparli wprowadzenie przepisów zakazujących reklamy papierosów, rozumiejąc, że obniży to koszty i zwiększy zyski w całej branży. Analiza ta może być istotna w wielu innych sytuacjach biznesowych związanych z reklamą. ^{[ potrzebne źródło ]}

Bez wykonalnych porozumień członkowie kartelu są również uwikłani w dylemat więźnia (w trybie wieloosobowym). „Współpraca” oznacza zazwyczaj utrzymywanie cen na wcześniej uzgodnionym poziomie minimalnym. „Dezercja” oznacza sprzedaż poniżej tego minimalnego poziomu i natychmiastowe odebranie interesów (i zysków) innym członkom kartelu. antymonopolowe chcą, aby potencjalni członkowie kartelu wzajemnie się zdradzali, zapewniając konsumentom możliwie najniższe ceny .

Sport

Jako przykład dylematu więźnia przytaczano doping w sporcie .

Dwóch rywalizujących sportowców ma możliwość zażycia nielegalnego i/lub niebezpiecznego narkotyku w celu zwiększenia swoich wyników. Jeśli żaden ze sportowców nie zażyje leku, żaden z nich nie uzyska przewagi. Jeśli tylko jeden tak zrobi, sportowiec uzyska znaczną przewagę nad konkurentem, zmniejszoną przez prawne i/lub medyczne niebezpieczeństwa wynikające z zażywania leku. Jeśli jednak obaj sportowcy zażyją lek, korzyści znikną, a pozostaną jedynie niebezpieczeństwa, co stawia ich obu w gorszej sytuacji, niż gdyby żaden z nich nie stosował dopingu.

W rozmowie z Kenem Griffeyem Jr. po sezonie MLB 1998 Barry Bonds wyraził swoją frustrację z powodu używania sterydów przez innych graczy. Bonds stwierdził: „Miałem w zeszłym roku piekielny sezon i nikogo to nie obchodziło. Nikt. Mimo że narzekałem na McGwire, Canseco i całe to gówno na sterydach, jestem zmęczony walką z tym. W tym roku kończę 35 lat rok. Zostały mi trzy lub cztery dobre sezony i chcę zarabiać. Po prostu zacznę brać jakieś hardkorowe rzeczy i mam nadzieję, że nie zaszkodzi to mojemu ciału. Potem wyjdę z tego grać i mieć to już za sobą.” Bonds znalazł się w dylemacie więźnia, jakim jest doping w baseballu, poczucie, że musi stosować sterydy, aby jego konkurenci nie mieli nad nim tak znaczącej przewagi, co stawia go na równych zasadach, choć wszyscy są w gorszej sytuacji niż gdyby nikt w ogóle nie stosował sterydów.

Polityka międzynarodowa

W teorii stosunków międzynarodowych dylemat więźnia jest często używany do wykazania, dlaczego współpraca kończy się niepowodzeniem w sytuacjach, gdy współpraca między państwami jest zbiorowo optymalna, ale indywidualnie nieoptymalna. Klasyczny przykład dylematu bezpieczeństwa przy czym wzrost bezpieczeństwa jednego państwa (np. zwiększenie jego siły militarnej) powoduje, że inne państwa obawiają się o własne bezpieczeństwo (ponieważ nie wiedzą, czy państwo zwiększające bezpieczeństwo zamierza wykorzystać swoją rosnącą siłę militarną do celów ofensywnych). W rezultacie środki zwiększające bezpieczeństwo mogą prowadzić do napięć, eskalacji lub konfliktu z jedną lub większą liczbą innych stron, dając wynik, którego żadna ze stron tak naprawdę nie pragnie; polityczny przykład dylematu więźnia. Dylemat bezpieczeństwa jest szczególnie dotkliwy w sytuacjach, gdy (1) trudno jest odróżnić broń ofensywną od broni defensywnej oraz (2) w każdym konflikcie przewagę ma atak nad obroną. Technologia wojskowa i geografia silnie wpływają na równowagę ataku i obrony.

Dylemat więźnia był często wykorzystywany przez realistycznych teoretyków stosunków międzynarodowych do wykazania, dlaczego wszystkie państwa (niezależnie od ich polityki wewnętrznej czy wyznawanej ideologii) w warunkach międzynarodowej anarchii będą miały trudności ze współpracą ze sobą, nawet jeśli wszystkie na takiej współpracy skorzystają.

Krytycy realizmu twierdzą jednak, że iteracja i poszerzanie cienia przyszłości to rozwiązania dylematu więźnia. Kiedy aktorzy raz odgrywają dylemat więźnia, mają motywację do ucieczki, ale kiedy spodziewają się, że będą grać w tę grę wielokrotnie, mają większą motywację do współpracy.

Dylematy gry wieloosobowej

Wiele rzeczywistych dylematów dotyczy wielu graczy. Tragedia dobra wspólnego Hardina , choć metaforyczna, może być postrzegana jako przykład uogólnienia PD w trybie dla wielu graczy: każdy wieśniak dokonuje wyboru dla osobistych korzyści lub dla ograniczenia. Zbiorową nagrodą za jednomyślną (lub nawet częstą) dezercję są bardzo niskie nagrody (reprezentujące zniszczenie „dobra wspólnego”). Powszechnym dylematem, z którym może się utożsamić większość ludzi, jest zmywanie naczyń we wspólnym domu. Nie myjąc naczyń, można zyskać, oszczędzając swój czas, ale jeśli wszyscy mieszkańcy przyjmą takie zachowanie, zbiorowym kosztem nie będą dla nikogo czyste talerze.

Nie zawsze wykorzystuje się to, co wspólne: William Poundstone w książce o dylemacie więźnia opisuje sytuację w Nowej Zelandii, gdzie skrzynki z gazetami pozostają otwarte. Możliwe jest, że ludzie przyjmą papier bez płacenia ( zdezerterują ), ale bardzo niewielu to robi, czując, że jeśli oni nie zapłacą, to inni też tego nie zrobią, niszcząc system. Późniejsze badania Elinor Ostrom , laureatki Nagrody Nobla w dziedzinie nauk ekonomicznych w 2009 roku postawił hipotezę, że tragedia dobra wspólnego jest nadmiernie uproszczona, a na jej negatywny wynik wpływają wpływy zewnętrzne. Bez komplikowania presji grupy komunikują się między sobą i zarządzają tym, co wspólne, dla obopólnych korzyści, egzekwując normy społeczne mające na celu ochronę zasobów i osiągnięcie maksymalnego dobra dla grupy, co jest przykładem wpływania na najlepszy wynik w przypadku PD.

Powiązane gry

Wymiana w zamkniętym worku

Dylemat więźnia jako wymiana teczki

Douglas Hofstadter zasugerował kiedyś, że ludziom często łatwiej jest zrozumieć problemy takie jak problem PD, gdy zilustruje się je w formie prostej gry lub kompromisu. Jednym z kilku przykładów, których użył, była „wymiana zamkniętych toreb”:

Spotykają się dwie osoby i wymieniają zamknięte torby, przy założeniu, że jedna z nich zawiera pieniądze, a druga zakup. Każdy z graczy może zdecydować się na wywiązanie się z umowy i włożyć do swojej torby to, na co się zgodził, lub może odstąpić od umowy, przekazując pustą torbę.

Przyjaciel czy wróg?

Przyjaciel czy wróg? to teleturniej emitowany od 2002 do 2003 roku w sieci Game Show Network w Stanach Zjednoczonych. Jest to przykład gry dylematu więźnia testowanej na prawdziwych ludziach, tyle że w sztucznej scenerii. W teleturnieju rywalizują ze sobą trzy pary osób. Kiedy para zostaje wyeliminowana, grają w grę podobną do dylematu więźnia, aby ustalić, w jaki sposób zostaną podzielone wygrane. Jeśli oboje współpracują (Przyjaciel), dzielą się wygraną 50–50. Jeżeli jeden współpracuje, a drugi wycofuje się (Wróg), dezerter otrzymuje całą wygraną, a współpracujący nic. Jeśli obaj odejdą, obaj odejdą z niczym. Zauważ, że macierz nagród różni się nieco od standardowej podanej powyżej, ponieważ nagrody w przypadku „obu defektów” i „współpracy, gdy przeciwnik defekt” są identyczne. To sprawia, że przypadek „oba defektów” jest słabą równowagą w porównaniu ze ścisłą równowagą w standardowym dylemacie więźnia. Jeśli uczestnik wie, że jego przeciwnik zagłosuje na „Wroga”, wówczas jego własny wybór nie wpływa na jego wygraną. W konkretnym sensie Przyjaciel czy wróg ma model nagród pomiędzy dylematem więźnia a grą w Kurczaka .

Macierz nagród to

Para 2 Para 1	„Przyjaciel” (współpraca)	„Wróg” (wada)
„Przyjaciel” (współpraca)	1 1	2 0
„Wróg” (wada)	0 2	0 0

Tę macierz wypłat wykorzystano także w brytyjskich programach telewizyjnych Trust Me , Shafted , The Bank Job i Golden Balls oraz w amerykańskich teleturniejach Take It All , a także w przypadku zwycięskiej pary w programach Reality Show Bachelor Pad i Love Wyspa . Dane gry ze Złotych Piłek seria została przeanalizowana przez zespół ekonomistów, który stwierdził, że współpraca była „zaskakująco wysoka” w przypadku kwot, które w prawdziwym świecie wydawałyby się znaczące, ale były stosunkowo niskie w kontekście gry.

Iterowana zaspa śnieżna

Naukowcy z Uniwersytetu w Lozannie i Uniwersytetu w Edynburgu zasugerowali, że „Iterowana gra w zaspę śnieżną” może lepiej odzwierciedlać rzeczywiste sytuacje społeczne. Chociaż ten model jest w rzeczywistości grą w kurczaka , zostanie on tutaj opisany. W tym modelu ryzyko bycia wyzyskiwanym w wyniku ucieczki jest niższe, a jednostki zawsze zyskują na wyborze opartym na współpracy. Gra o zaspie śnieżnej przedstawia dwóch kierowców, którzy utknęli po przeciwnych stronach zaspy , z których każdy ma możliwość odgarnięcia śniegu w celu oczyszczenia ścieżki lub pozostania w samochodzie. Największą zapłatą dla gracza jest pozostawienie przeciwnika, aby sam odśnieżył cały śnieg, ale przeciwnik nadal jest nominalnie nagradzany za swoją pracę.

Może to lepiej odzwierciedlać scenariusze ze świata rzeczywistego – badacze podają przykład dwóch naukowców współpracujących nad raportem, przy czym obaj odnieśliby korzyści, gdyby drugi pracował ciężej. „Ale jeśli Twój współpracownik nie wykonuje żadnej pracy, prawdopodobnie lepiej będzie, jeśli wykonasz całą pracę samodzielnie. Nadal będziesz mieć ukończony projekt”.

Przykładowe wypłaty za zaspę śnieżną (A, B)
B A	Współpracuje	Wady
Współpracuje	500, 500	200, 800
Wady	800, 200	0, 0

Przykładowe wypłaty PD (A, B)
B A	Współpracuje	Wady
Współpracuje	500, 500	−200, 1200
Wady	1200, -200	0, 0

Gry koordynacyjne

W grach koordynacyjnych gracze muszą koordynować swoje strategie, aby uzyskać dobry wynik. Przykładem są dwa samochody, które nagle spotykają się podczas zamieci; każdy musi wybrać, czy skręcić w lewo, czy w prawo. Jeżeli obydwa skręcają w lewo lub obydwa w prawo, samochody nie zderzają się. W koordynacji działań pomaga lokalna konwencja ruchu lewostronnego i prawostronnego .

Symetryczne gry koordynacyjne obejmują polowanie na jelenie oraz Bacha lub Strawińskiego .

Asymetryczne dylematy więźnia

Bardziej ogólny zestaw gier jest asymetryczny. Podobnie jak w przypadku dylematu więźnia, najlepszym rezultatem jest współpraca, a istnieją motywy ucieczki. Jednak w przeciwieństwie do dylematu symetrycznego więźnia, jeden z graczy ma więcej do stracenia i/lub więcej do zyskania niż drugi. Niektóre takie gry zostały opisane jako dylemat więźnia, w którym jeden więzień ma alibi , stąd termin „gra alibi”.

W eksperymentach gracze uzyskujący nierówne wypłaty w powtarzających się grach mogą dążyć do maksymalizacji zysków, ale tylko pod warunkiem, że obaj gracze otrzymają równe wypłaty; może to prowadzić do stabilnej strategii równowagi, w której pokrzywdzony gracz popełnia błędy w każdej grze X, podczas gdy drugi zawsze współpracuje. Takie zachowanie może zależeć od norm społecznych eksperymentu dotyczących uczciwości.

Dylemat Strażnika

Nie tylko więźniowie stają przed dylematami. Strażnicy konfrontują się także z sytuacjami, w których do wyboru są jedynie nieatrakcyjne wybory. Przykłady można łatwo znaleźć w przypadkach, gdy jeden agent musi załagodzić napięcia między swoimi własnymi partnerami: można pomyśleć o dwóch kolegach walczących o awans zawodowy i kłopotach, jakie powoduje to dyrektor zarządzający ich firmy ; dwóch urzędników rywalizujących o awans i napięcie, jakie to powoduje dla szefa ich biura ; lub w rodzicielstwie gdy dwójka rodzeństwa rywalizuje o uwagę i niepokój, jaki powoduje to u rodziców. Jeśli zachowanie opiekuna satysfakcjonuje jedną stronę, druga strona czuje się odsłonięta i wyobcowana.

Z perspektywy stosunków międzynarodowych dr Spyros Katsoulas wprowadza koncepcję dylematu opiekuna. Dylemat strażnika definiuje się jako stan, w którym dwa państwa utrzymują wobec siebie wrogość, pomimo posiadania silniejszego wspólnego sojusznika. Domyślnie dylematem jest sytuacja, w której dokonano niezadowalających wyborów. Dylemat strażnika polega na tym, że silniejsze państwo nie może ani uniknąć kryzysu pomiędzy swoimi sojusznikami, ani aktywnie się w niego zaangażować, nie naruszając kruchej równowagi. Jeśli opiekun wstrzyma się od głosu, sytuacja może wymknąć się spod kontroli; jeśli opiekun się w to zaangażuje, jakiekolwiek przechylenie w jedną stronę może zostać odebrane jako zwycięstwo lub szansa dla drugiej. Rozwijanie się W koncepcji dylematu bezpieczeństwa sojuszu Glenna Snydera wyniki interakcji pomiędzy strażnikiem a dwoma mniejszymi partnerami opisuje się jako porzucenie, uwięzienie i ośmielenie.

Oprogramowanie

Stworzono kilka pakietów oprogramowania do przeprowadzania symulacji dylematu więźnia i turniejów, z których część ma dostępny kod źródłowy.

Kod źródłowy drugiego turnieju prowadzonego przez Roberta Axelroda (napisany przez Axelroda i wielu współpracowników w Fortranie ) jest dostępny online
Prison , biblioteka napisana w Javie , ostatnia aktualizacja w 1998 roku
Axelrod-Python , napisany w Pythonie
Evoplex , szybki program do modelowania agentowego wydany w 2018 roku przez Marcosa Cardinota

W fikcji

Hannu Rajaniemi umieścił scenę otwierającą swoją trylogię The Quantum Thief w „więzieniu dylematów”. Główny temat serii został opisany jako „nieadekwatność binarnego wszechświata”, a ostatecznym antagonistą jest postać zwana All-Defector. Rajaniemi jest matematykiem z wykształceniem Cambridge i posiada stopień doktora. w fizyce matematycznej - wymienność materii i informacji jest główną cechą książek, których akcja rozgrywa się w przyszłości „po osobliwości”. Pierwsza książka z tej serii została opublikowana w 2010 roku i zawierała dwie kontynuacje: The Fractal Prince i The Causal Angel , opublikowane odpowiednio w 2012 i 2014 roku.

Gra wzorowana na (iterowanym) dylemacie więźnia jest głównym tematem gry wideo Zero Escape: Virtue's Last Reward z 2012 roku i niewielką częścią jej kontynuacji Zero Escape: Zero Time Dilemma z 2016 roku .

W Tajemnicze Towarzystwo Benedykta i dylemat więźnia autorstwa Trentona Lee Stewarta główni bohaterowie zaczynają od zagrania w pewną wersję gry i całkowitej ucieczki z „więzienia”. Później stają się prawdziwymi więźniami i ponownie uciekają.

W podarcie Strefa przygód : Równowaga podczas gry w cierpienie postacie graczy dwukrotnie stają przed dylematem więźnia podczas pobytu w domenie dwóch liszów, raz współpracując, a raz uciekając.

W ósmej powieści autora Jamesa SA Corey Tiamat's Gniew Winston Duarte wyjaśnia dylemat więźnia swojej 14 - letniej córce Teresie, aby przeszkolić ją w myśleniu strategicznym. ^{[ potrzebne źródło ]}

Skrajną wersję dylematu więźnia przedstawiono w filmie Mroczny rycerz z 2008 roku , w którym Joker ustawia dwa promy, jeden z więźniami, a drugi z cywilami, uzbrajając obie grupy w środki umożliwiające wzajemne zdetonowanie bomby na promach drugiej strony. Ostatecznie obie strony decydują się nie podejmować działań.

Zobacz też

Dalsza lektura

Amadae, S. (2016). „Dylemat więźnia” , Więźniowie rozumu . Cambridge University Press , Nowy Jork, s. 24–61.
Aumann, Robert (1959). „Dopuszczalne punkty w ogólnych grach kooperacyjnych n -osobowych”. W Luce, Dakota; Tucker, AW (red.). Wkład do teorii gier 23 IV . Roczniki Studium Matematyki. Tom. 40. Princeton New Jersey: Princeton University Press. s. 287–324. MR 0104521 .
Axelrod, R. (1984). Ewolucja współpracy . ISBN 0-465-02121-2
Bicchieri, Cristina (1993). Racjonalność i koordynacja. Wydawnictwo Uniwersytetu Cambridge .
Szachy, David M. (grudzień 1988). „Symulowanie ewolucji zachowania: problem powtarzalnego dylematu więźnia” (PDF) . Złożone systemy . 2 (6): 663–70. Zarchiwizowane (PDF) od oryginału w dniu 30.05.2015 r.
Collins, Rory W. (marzec 2022). „Paradoks dylematu więźnia: racjonalność, moralność i wzajemność” . Pomyśl: filozofia dla każdego . 21 (61): 45–55. doi : 10.1017/S1477175621000464 .
Dresher, M. (1961). Matematyka gier strategicznych: teoria i zastosowania Prentice-Hall , Englewood Cliffs, NJ.
Greif, A. (2006). Instytucje i droga do nowoczesnej gospodarki: lekcje ze średniowiecznego handlu. Cambridge University Press, Cambridge , Wielka Brytania.
Kopelman, Shirli (luty 2020). „Wet za wet i nie tylko: legendarne dzieło Anatola Rapoporta” . Badania nad negocjacjami i zarządzaniem konfliktami . 13 (1): 60–84. doi : 10.1111/ncmr.12172 .
Poundstone, William (1993). Dylemat więźnia (wyd. 1. Anchor Books). Nowy Jork: Kotwica. ISBN 0-385-41580-X .
Rapoport, Anatol i Albert M. Chammah (1965). Dylemat więźnia . Wydawnictwo Uniwersytetu Michigan .
Schneider, Marek; Shields, Timothy W. (czerwiec 2022). „Motywy współpracy w dylemacie jednorazowego więźnia” . Journal of finansów behawioralnych . 23 (4): 438–456. doi : 10.1080/15427560.2022.2081974 .

Linki zewnętrzne

Media związane z dylematem więźnia w Wikimedia Commons
Dylemat więźnia ( Encyklopedia filozofii Stanforda )
Dylemat Bowerbirda Dylemat więźnia w ornitologii – komiks matematyczny Larry'ego Gonicka.
Dylemat więźnia Dylemat więźnia z minifigurkami Lego.
Dixit, Avinash ; Nalebuff, Barry (2008). „Dylemat więźnia” . W David R. Henderson (red.). Zwięzła Encyklopedia Ekonomii (wyd. 2). Indianapolis: Biblioteka Ekonomii i Wolności . ISBN 978-0865976658 . OCLC 237794267 .
Teoria gier 101: Dylemat więźnia
Dawkins: Mili goście kończą pierwsi
Biblioteka Pythona dla dylematu więźnia Axelroda
Zagraj w Dylemat więźnia na oTree (nie dotyczy 11-5-17)
Ewolucja zaufania Nicky'ego Case'a , przykład gry w darowizny
Gra internetowa Iterated Prisoner's Dilemma autorstwa Wayne'a Davisa

Paradoksy
Filozoficzny	Analiza Most Buridana Argument marzeń epikurejczyk Fikcja Znajomość Fitcha Wolna wola Goodmana Hedonizm Liberał Meno Zwykły dodatek Moore'a Newcomba Nihilizm Wszechmoc Przedmowa Przestrzeganie zasad Soryt Statek Tezeusza biały koń Zenona
Logiczny	Fryzjer Jagoda Bhartrhariego Burali-Forti Sąd Krokodyl Curry’ego Epimenides Paradoks wolnego wyboru Grellinga-Nelsona Kleene–Rosser Kłamca Karta Nie? Nie Pinokio Quine’a Yabla Dzień na odwrót Paradoksy teorii mnogości Richarda Russella Sokratejski hotelu Hilberta Paradoks temperatury Fryzjer Złap 22 Kurczak lub jajko Pijący Majorat Loteria Broda Platona Kruk Rossa Nieoczekiwane powieszenie „ Co żółw powiedział Achillesowi ” Paradoks śmierci cieplnej Paradoks Olbersa
Gospodarczy	Allais Antymonopolowe Informacje o strzałce Bertranda Braessa Konkurs Dochód i płodność Downs – Thomson Easterlina Edgewortha Ellsberga europejski Gibsona Giffen dobrze Ikar Jevonsa Leontiefa Lerner Lucas Mandeville'a Mayfielda Metzlera Mnóstwo Wydajność Dobrobyt Ścitowski Odzyskiwanie usługi Petersburg Oszczędność Trud Tullock Wartość
Teoria decyzji	Abilene Podział Alabama Nowe stany Populacja Strzałka Tyłek Buridana Sieci sklepów Condorceta Podejmowanie decyzji Upadki Ellsberga Fenno Fredkina Zielony Jeż Wynalazca Zagadka toksyn Kavki Widelec Mortona Nawigacja Newcomba Parrondo Gotowość Zapobieganie Dylemat więźnia Tolerancja Siła woli
Lista Kategoria

Zagadnienia z teorii gier
Definicje	Gra w zagęszczenie Gra kooperacyjna Determinacja Eskalacja zaangażowania Gra w rozbudowanej formie Wygrywa pierwszy i drugi gracz Złożoność gry Gra graficzna Hierarchia przekonań Zestaw informacji Gra w normalnej formie Pierwszeństwo Gra sekwencyjna Symultaniczna gra Jednoczesny wybór akcji Rozwiązana gra Zwięzła gra
Pojęcia równowagi	Równowaga Bayesa Nasha Równowaga Berge’a Rdzeń Skorelowana równowaga Równowaga epsilon Strategia stabilna ewolucyjnie Równowaga Gibbsa Równowaga stabilna Mertensa Doskonała równowaga Markowa Równowaga Nasha Efektywność Pareta Doskonała równowaga Bayesa Właściwa równowaga Równowaga odpowiedzi kwantowej Równowaga quasi-idealna Dominacja ryzyka Równowaga satysfakcji Samopotwierdzająca się równowaga Równowaga sekwencyjna wartość Shapley’a Silna równowaga Nasha Perfekcja podgry Drżąca ręka
Strategie	Indukcja wsteczna Cieniowanie stawek Zmowa Indukcja do przodu Ponury spust Strategia Markowa Strategie dominujące Czysta strategia Strategia mieszana Argument kradzieży strategii Wet za wet
Zajęcia z gier	Problem z targowaniem się Tania rozmowa Globalna gra Gra nieprzechodnia Gra na średnim boisku Projekt mechanizmu gra n -osobowa Doskonała informacja Duża gra Poissona Potencjalna gra Powtórzona gra Gra ekranowa Gra sygnalizacyjna Konkurs Stackelberga Ściśle zdeterminowana gra Gra stochastyczna Gra symetryczna Gra o sumie zerowej
Gry	Iść Szachy Nieskończone szachy Warcaby Kółko i krzyżyk Dylemat więźnia Gra polegająca na wymianie prezentów Opcjonalny dylemat więźnia Dylemat podróżnika Gra koordynacyjna Kurczak Gra stonoga Gra sygnalizacyjna Lewisa Dylemat wolontariusza Aukcja dolara Wojna płci Polowanie na jelenia Pasujące grosze Gra w ultimatum Nożyczki do papieru kamiennego Gra piracka Gra dyktatora Gra dóbr publicznych Gra Blotto Wojna na wyniszczenie Problem z barem El Farol Uczciwy podział Uczciwe krojenie ciasta Gra Cournota Impas Dylemat Dinera Zgadnij 2/3 średniej Poker Kuhna Gra negocjacyjna Nasha Zagadki indukcyjne Zaufaj grze Gra Księżniczka i potwór Problem ze spotkaniem
Twierdzenia	Twierdzenie Arrowa o niemożliwości Twierdzenie o zgodności Aumanna Twierdzenie ludowe Twierdzenie Minimaxa Twierdzenie Nasha Twierdzenie o oczyszczaniu Zasada objawienia Twierdzenie Zermelo
Kluczowe dane	Alberta W. Tuckera Amosa Twerskiego Antoine’a Augustina Cournota Ariela Rubinsteina Claude'a Shannona Daniela Kahnemana Davida K. Levine’a David M. Kreps Donalda B. Gilliesa Drew Fudenberg Eryk Maskin Harolda W. Kuhna Herberta Szymona Herve Moulin Johna Conwaya Jana Tyrola Jean-François Mertensa Jennifer Tour Chayes Johna Harsanyi’ego Johna Maynarda Smitha Johna Nasha Johna von Neumanna Kennetha Arrowa Kennetha Binmore’a Leonida Hurwicza Lloyda Shapleya Melvina Dreshera Merrill M. Powódź Olga Bondarewa Oskara Morgensterna Pawła Milgroma Peytona Younga Reinharda Seltena Roberta Axelroda Roberta Aumanna Roberta B. Wilsona Rogera Myersona Samuela Bowlesa Zuzanna Scotchmer Thomasa Schellinga Williama Vickreya
Różnorodny	Aukcja za całość Przycinanie alfa-beta Paradoks Bertranda Ograniczona racjonalność Kombinatoryczna teoria gier Analiza konfrontacji Kokonkurencyjność Ewolucyjna teoria gier Przewaga pierwszego ruchu w szachach Język opisu gry Mechanika gry Słowniczek teorii gier Lista teoretyków gier Lista gier w teorii gier Sytuacja bez wygranej Rozwiązywanie szachów Gra topologiczna Tragedia wspólnego pastwiska Tyrania małych decyzji

Kontrola władzy
Biblioteki Narodowe	Hiszpania Francja Dane BnF Niemcy Izrael Stany Zjednoczone
Inny	SZYBKO IdRef 2