Definiowanie równania (fizyka)

Aby zapoznać się ze wspólną nomenklaturą wielkości podstawowych używanych w tym artykule, zobacz wielkość fizyczną . Aby zapoznać się z modyfikacjami 4-wektorowymi stosowanymi w teorii względności, zobacz czterowektorowe .

W fizyce równania definiujące to równania , które definiują nowe wielkości w kategoriach wielkości podstawowych. W tym artykule zastosowano obecny system jednostek SI , a nie jednostki naturalne lub charakterystyczne .

Opis jednostek i wielkości fizycznych

Ilości fizyczne i jednostki mają tę samą hierarchię; wybrane wielkości podstawowe mają określone jednostki podstawowe , z których można wyprowadzić dowolne inne wielkości , które mają odpowiednie jednostki pochodne .

Analogia mieszania kolorów

Definiowanie ilości jest analogiczne do mieszania kolorów i można je klasyfikować w podobny sposób, chociaż nie jest to standardowe. Kolory podstawowe dotyczą ilości podstawowych; tak jak kolory drugorzędne (lub trzeciorzędowe itp.) mają się do wielkości pochodnych. Mieszanie kolorów jest analogiczne do łączenia wielkości za pomocą działań matematycznych. Ale kolory mogą być dla światła lub farby , i analogicznie system jednostek może mieć jedną z wielu form: takich jak SI (obecnie najczęściej), CGS , Gaussa , stare jednostki imperialne , specyficzna forma jednostek naturalnych lub nawet arbitralnie zdefiniowane jednostki charakterystyczne dla rozważanego układu fizycznego ( jednostki charakterystyczne ).

Wybór podstawowego systemu wielkości i jednostek jest arbitralny; ale raz wybrany musi być przestrzegany podczas całej analizy, która następuje dla zachowania spójności. Mieszanie różnych systemów jednostek nie ma sensu. Wybór systemu jednostek, jednego systemu z SI, CGS itp., jest jak wybór, czy użyć farby, czy jasnych kolorów.

W świetle tej analogii definicje pierwotne to wielkości podstawowe bez definiującego równania, ale zdefiniowane warunki standardowe, definicje „drugorzędne” to wielkości zdefiniowane wyłącznie za pomocą wielkości podstawowych, „trzeciorzędowe” dla wielkości zarówno pod względem wielkości podstawowych, jak i „wtórnych” , „czwartorzędowy” dla ilości wyrażonych jako ilości podstawowe, „drugorzędne” i „trzeciorzędowe” i tak dalej.

Motywacja

Wiele dziedzin fizyki wymaga definicji, aby równania miały sens.

Implikacje teoretyczne: Definicje są ważne, ponieważ mogą prowadzić do nowego spojrzenia na dziedzinę fizyki. Dwa takie przykłady wystąpiły w fizyce klasycznej. Kiedy entropię S – zakres termodynamiki został znacznie rozszerzony poprzez powiązanie chaosu i nieporządku z wielkością liczbową, która mogła odnosić się do energii i temperatury, co doprowadziło do zrozumienia drugiej zasady termodynamiki i mechaniki statystycznej .

Również funkcjonał działania (również zapisywany jako S ) (wraz z uogólnionymi współrzędnymi i pędami oraz funkcją Lagrange'a ), początkowo alternatywne sformułowanie mechaniki klasycznej do praw Newtona , obecnie rozszerza zakres współczesnej fizyki w ogóle - zwłaszcza mechaniki kwantowej , fizyki cząstek elementarnych , i ogólnej teorii względności .

Wygoda analityczna: pozwalają na bardziej zwięzłe zapisywanie innych równań, a tym samym umożliwiają łatwiejszą manipulację matematyczną; poprzez włączenie parametru do definicji, wystąpienia parametru mogą zostać wchłonięte do wielkości podstawionej i usunięte z równania.

Przykład

0 Jako przykład rozważmy prawo obwodu Ampère'a (z poprawką Maxwella) w postaci całkowej dla dowolnego przewodnika przewodzącego prąd w próżni (a więc zero namagnesowania spowodowanego ośrodkiem, tj. M = ):

$${\ Displaystyle \ punkt _ {S} \ mathbf {B} \ cdot d \ mathbf {l} = \ mu _ {0 }\oint _{S}\left(\mathbf {J} +\varepsilon _{0}{\frac {\częściowy \mathbf {E}}}{\częściowy t}}\right)\cdot d\mathbf {A } }$$

korzystając z definicji konstytutywnej

$${\ Displaystyle \ mathbf {B} = \ mu _ {0} \ mathbf {H},}$$

oraz definicja gęstości prądu

$${\ Displaystyle I = \ oint _ {S} \ mathbf {J} \ cdot d \ mathbf {A},}$$

podobnie dla gęstości prądu przesunięcia

$${\ Displaystyle \ mathbf {J} _ {\ rm {d}} = \ epsilon _ {0} {\ Frac {\ częściowy \ mathbf {E}} {\ częściowy t}}}$$

prowadząc do prądu przesunięcia

$${\ Displaystyle I_ {d} = \ punkt _ {S} \ mathbf {J} _ {\ tekst {d}} \ cdot d \ mathbf {A},}$$

mamy

$${\ Displaystyle \ oint _ {S} \ mathbf {B} \ cdot d \ mathbf {l} = \ mu _ {0}\oint _{S}\mathbf {J} \cdot d\mathbf {A} +\mu _{0}\oint _{S}\mathbf {J} _{\text{d}}\cdot d\mathbf {A} ,}$$

$${\ Displaystyle \ punkt _ {S} \ mathbf {H} \ cdot d \ mathbf {l} = I + I_ {d},}$$

co jest prostsze do zapisania, nawet jeśli równanie jest takie samo.

Łatwość porównania: Umożliwiają dokonywanie porównań pomiarów, gdy w przeciwnym razie mogą wydawać się niejednoznaczne i niejasne.

Przykład

Podstawowym przykładem jest gęstość masy. Nie jest jasne, jak porównać, ile materii składa się z różnych substancji, biorąc pod uwagę tylko ich masy lub tylko ich objętości. Biorąc pod uwagę oba dla każdej substancji, masa m na jednostkę objętości V lub gęstość masy ρ zapewnia sensowne porównanie między substancjami, ponieważ dla każdej ustalonej objętości odpowiada ilości masy zależnej od substancji. Aby to zilustrować; jeżeli dwie substancje A i B mają odpowiednio masy m _A i m _B , zajmując odpowiednio objętości V _A i V _B , to korzystając z definicji gęstości masy otrzymujemy:

ρ _ZA = m _ZA / V _ZA , ρ _b = m _b / V _b

po tym widać, że:

• jeśli m _ZA > m _B lub m _ZA < m _B i V _ZA = V _B , to ρ _ZA > ρ _B lub ρ _ZA < ρ _B ,
• jeśli m _ZA = m _B i V _A > V _B lub V _ZA < V _B , to ρ _ZA < ρ _B lub ρ _A > ρ _B ,
• jeśli ρ _A = ρ _B , to m _A / V _A = m _B / V _B więc m _A / m _B = V _A / V _B , wykazując, że jeśli m _A > m _B lub m _A < m _B , to V _A > V _B lub V _A < V _B .

Dokonywanie takich porównań bez logicznego użycia matematyki w ten sposób nie byłoby tak systematyczne.

Budowa równań definiujących

Zakres definicji

Równania definiujące są zwykle formułowane w kategoriach algebry elementarnej i rachunku różniczkowego , algebry wektorów i rachunku różniczkowego lub w najbardziej ogólnych zastosowaniach algebry tensorowej i rachunku różniczkowego , w zależności od poziomu studiów i prezentacji, złożoności tematu i zakresu zastosowania. Funkcje mogą być włączone do definicji, w przypadku rachunku różniczkowego jest to konieczne. Ilości mogą być również zespolonymi dla korzyści teoretycznych, ale dla pomiaru fizycznego istotna jest część rzeczywista, część urojoną można odrzucić. W przypadku bardziej zaawansowanych zabiegów może być konieczne zapisanie równania w równoważnej, ale alternatywnej formie przy użyciu innych równań definiujących, aby definicja była użyteczna. Często definicje mogą zaczynać się od algebry elementarnej, następnie modyfikować do wektorów, a następnie w granicznych przypadkach można użyć rachunku różniczkowego. Różne poziomy stosowanej matematyki zazwyczaj są zgodne z tym wzorem.

Zazwyczaj definicje są jawne, co oznacza, że ​​przedmiotem równania jest wielkość definiująca, ale czasami równanie nie jest zapisywane jawnie — chociaż można rozwiązać wielkość definiującą, aby równanie było wyraźne. W przypadku równań wektorowych czasami wielkość definiująca jest iloczynem krzyżowym lub kropkowym i nie można jej rozwiązać jawnie jako wektora, ale składniki mogą.

Strumień F przez powierzchnię , d S jest elementem pola wektora różniczkowego , n jest jednostką normalną do powierzchni. W przypadku przykładów fizycznych tutaj gęstość prądu J lub pole magnetyczne B to F na schemacie.

Moment pędu; składowe skalarne i wektorowe.

Przykłady

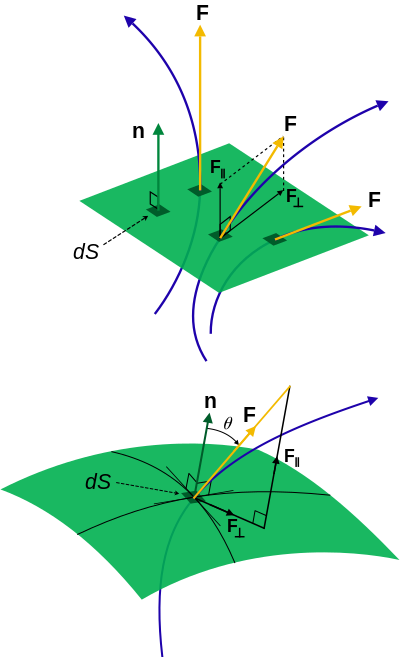
Gęstość prądu elektrycznego jest przykładem obejmującym wszystkie te metody, moment pędu to przykład, który nie wymaga rachunku różniczkowego. Zobacz sekcję mechaniki klasycznej poniżej, aby zapoznać się z nazewnictwem i diagramami po prawej stronie.

Algebra elementarna

Operacje to po prostu mnożenie i dzielenie. Równania można zapisać w postaci iloczynu lub ilorazu, obie oczywiście równoważne.

	Moment pędu	Gęstość prądu elektrycznego
Forma ilorazowa	${\ Displaystyle p = {\ Frac {L} {r}} \, \!}$	${\ Displaystyle J = {\ Frac {I} {A}} \, \!}$
Formularz produktu	${\ Displaystyle L = pr \, \!}$	${\ Displaystyle I = JA \, \!}$

Algebra wektorów

Nie ma możliwości podzielenia wektora przez wektor, więc nie ma form iloczynu ani ilorazu.

	Moment pędu	Gęstość prądu elektrycznego
Forma ilorazowa	Nie dotyczy	${\ Displaystyle \ mathbf {J} \ cdot \ mathbf {\ kapelusz {n}} = {\ Frac {I} {A}} \, \!}$
Formularz produktu	Zaczynając od ${\ Displaystyle L = pr, \, \!}$ 0 ponieważ L = gdy p i r są równoległe lub antyrównoległe i jest maksimum, gdy są prostopadłe, tak że jedynym składnikiem p , który przyczynia się do L , jest styczna | p | sin θ , wartość momentu pędu L należy przepisać jako ${\ Displaystyle L = pr \ sin \ teta. \, \!}$ Ponieważ r , p i L tworzą prawą triadę, prowadzi to do postaci wektorowej ${\ Displaystyle \ mathbf {L} = \ mathbf {r} \ razy \ mathbf {p}. \, \!}$	${\ Displaystyle \ mathbf {J} \ cdot \ mathbf {\ kapelusz {n}} A = ja, \, \!}$ ${\ Displaystyle \ mathbf {J} \ cdot \ mathbf {A} = ja, \, \!}$

Rachunek elementarny

Operacje arytmetyczne są modyfikowane do granicznych przypadków różniczkowania i całkowania. Równania można wyrazić na te równoważne i alternatywne sposoby.

	Gęstość prądu
Forma różniczkowa	$\ Displaystyle J = \ lim _ {A \ rightarrow 0} {\ Frac {I} {A}} = {\ Frac {\ operatorname {d} I} {\ matematyczna {d} A}}\,\!}$
Forma integralna	$ZA {\ Displaystyle I = \ lim _ {A_ {i} \ rightarrow 0} \ suma _ {i} JA_ {i} = \ int _$ gdzie d A oznacza różniczkowy element powierzchniowy (patrz także całka powierzchniowa ). Alternatywnie dla formy integralnej ${\ Displaystyle \ operatorname {d} ja = J {\ operatorname {d} A}, \, \!}$ ${\ Displaystyle I = \ int _ {S} J {\ operatorname {d} A}. \, \!}$

Rachunek wektorowy

	Gęstość prądu
Forma różniczkowa	${\ Displaystyle \ mathbf {J} \ cdot \ mathbf {\ kapelusz {n}} = {\ Frac {\ operatorname {d} I} {\ operatorname {d} A}} \ ,\!}$
Forma integralna	${\ Displaystyle I = \ int _ {S} \ mathbf {J} \ cdot \ operatorname {d} \ mathbf {A} \, \!}$ gdzie d A = n d A jest polem wektora różniczkowego .

Analiza tensorowa

tensorami rzędu 1 . Poniższe wzory to nic innego jak równania wektorowe w języku tensorów.

	Moment pędu	Gęstość prądu elektrycznego
Forma różniczkowa	Nie dotyczy	${\ Displaystyle J_ {i} n_ {i} = {\ Frac {\ operatorname {d} ja} {\ operatorname {d} A}} \, \!$
Forma produktu/integralna	Zaczynając od ${\ Displaystyle \ mathbf {L} = \ mathbf {r} \ razy \ mathbf {p} \, \!}$ składnikami są L i , r j , pi , gdzie i, j, k są indeksami fikcyjnymi, z których każdy przyjmuje wartości 1, 2, 3, używając identyczności z analizy tensorowej $\ Displaystyle \ mathbf {a} = \ mathbf {b} \ razy \ mathbf {c} \ quad a_ {i} = \ epsilon _ {ijk}b_{j}c_{k},\,\!}$ gdzie ε ijk jest permutacją/tensorem Levi-Cita , prowadzi do ${\ Displaystyle L_ {i} = \ epsilon _ {ijk} r_ {j} p_ {k}. \, \!}$	Korzystając z konwencji sumowania Einsteina , $\ Displaystyle J_ {i} n_ {i} \ operatorname {d} A = \ operatorname {d} ja \, \!}$ $\ Displaystyle \ int _ {S} J_ {i} \ operatorname {d} A_ {i} = ja \, \!}$

Definicje wielokrotnego wyboru

Czasami istnieje jeszcze dowolność w wybranym systemie jednostek, aby zdefiniować jedną lub więcej wielkości na więcej niż jeden sposób. Sytuacja dzieli się na dwa przypadki:

Wzajemnie wykluczające się definicje: Istnieje wiele możliwych opcji definiowania wielkości w kategoriach innych, ale można użyć tylko jednej, a innych nie. Wybór więcej niż jednego wyłącznego równania dla definicji prowadzi do sprzeczności – jedno równanie może wymagać, aby wielkość X była zdefiniowana w jeden sposób za pomocą innej wielkości Y , podczas gdy inne równanie wymaga odwrotności , Y należy zdefiniować za pomocą X , ale potem inne równanie może sfałszować użycie zarówno X , jak i Y , i tak dalej. Wzajemna niezgoda uniemożliwia stwierdzenie, które równanie określa jaką wielkość.

Równoważne definicje: Definiowanie równań, które są równoważne i samozgodne z innymi równaniami i prawami w ramach teorii fizycznej, po prostu zapisywane na różne sposoby.

W każdym przypadku są dwie możliwości:

Jedno równanie definiujące – jedna zdefiniowana wielkość: Równanie definiujące służy do zdefiniowania jednej wielkości w odniesieniu do wielu innych.

Jedno równanie definiujące – liczba zdefiniowanych wielkości: Równanie definiujące służy do definiowania wielu wielkości w odniesieniu do wielu innych. Pojedyncze równanie definiujące nie powinno zawierać jednej wielkości definiującej wszystkie inne wielkości w tym samym równaniu , w przeciwnym razie ponownie pojawią się sprzeczności. Nie ma oddzielnej definicji zdefiniowanych wielkości, ponieważ są one zdefiniowane przez jedną wielkość w jednym równaniu. Ponadto zdefiniowane wielkości mogły być już wcześniej zdefiniowane, więc jeśli inna wielkość definiuje je w tym samym równaniu, dochodzi do kolizji między definicjami.

Sprzeczności można uniknąć, definiując kolejno wielkości ; kolejność , musi być uwzględniona. Przykłady obejmujące te przypadki występują w elektromagnetyzmie i są podane poniżej.

Różnicowa siła magnetyczna d F spowodowana małym elementem ładunkowym d q tworzącym prąd elektryczny I ( używany jest prąd konwencjonalny ). Siła musi być całkowana liniowo wzdłuż ścieżki przepływu prądu względem elementu linii wektora d r .

Przykłady

Wzajemnie wykluczające się definicje:

Pole indukcji magnetycznej B można zdefiniować za pomocą ładunku elektrycznego q lub prądu I , a siłę Lorentza (człon magnetyczny) F , której doświadczają nośniki ładunku z powodu pola,

$\ Displaystyle {\ rozpocząć {wyrównane} \ mathbf {F} & = q \ lewo (\ mathbf {v} \ razy \ mathbf {B} \ prawej) \\& = \ lewo (\ int I \ operatorname {d} t\right)\left({\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}\times \mathbf {B} \right)\\&=\left (\int I\mathrm {d} t{\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}\right)\times \mathbf {B} \\&=I\ left(\int \mathrm {d} \mathbf {r} \right)\times \mathbf {B} \\&=I\left(\mathbf {l} \times \mathbf {B} \right),\end {wyrównany}}\,\!}$

gdzie ${\ Displaystyle \ mathbf {l} = \ int \ operatorname {d} \ mathbf {r} \, \!}$ to zmiana położenia, przez które przechodzą nośniki ładunku (zakładając, że prąd jest niezależny od położenia, jeśli nie, całka po linii musi być wykonana wzdłuż ścieżki prądu) lub w kategoriach strumienia magnetycznego Φ _b przez powierzchnię S , gdzie obszar jest używany jako skalar A i wektor: ${\ Displaystyle \ mathbf {A} = A \ mathbf {\ kapelusz {n}} \, \!}$ i ${\ Displaystyle \ mathbf {\ kapelusz {n}} \, \!}$ jest jednostką normalną do A , albo różniczkową formularz

${\ Displaystyle \ mathbf {B} \ cdot \ mathbf {\ kapelusz {n}} = {\ Frac {\ operatorname {d} \ Phi _ {B}} {\ operatorname {d} A}},\,\!}$

lub w formie integralnej,

${\ Displaystyle \ mathbf {B} \ cdot \ mathbf {\ kapelusz {n}} \ operatorname {d} A = \ operatorname {d} \ Phi _ {B} \ ,\!}$

${\ Displaystyle \ Phi _ {B} = \ int _ {S} \ mathbf {B} \ cdot \ operatorname {d} \ mathbf {A}. \, \!}$

Jednak tylko jedno z powyższych równań może być użyte do zdefiniowania B z następującego powodu, biorąc pod uwagę, że A , r , v i F zostały jednoznacznie zdefiniowane gdzie indziej (najprawdopodobniej mechanika i geometria euklidesowa ).

Jeśli równanie siły definiuje B , gdzie wcześniej zdefiniowano q lub I , to równanie strumienia definiuje Φ _B , ponieważ B zostało wcześniej zdefiniowane jednoznacznie. Jeżeli równanie strumienia określa B , gdzie Φ _B , równanie siły może być równaniem definiującym dla I lub q . Zwróć uwagę na sprzeczność, gdy B oba równania definiują B jednocześnie i gdy B nie jest wielkością bazową; równanie siły wymaga, aby q lub I było zdefiniowane w innym miejscu, podczas gdy równanie strumienia wymaga, aby q lub I były zdefiniowane przez równanie siły, podobnie równanie siły wymaga, aby Φ _B było zdefiniowane przez równanie strumienia, w tym samym czasie równanie strumienia wymaga, aby Φ _B było zdefiniowane gdzie indziej. Aby oba równania mogły być używane jednocześnie jako definicje, B musi być wielkością podstawową, tak aby można było zdefiniować F i Φ _{B jako} jednoznacznie wynikające z B.

Równoważne definicje:

Innym przykładem jest indukcyjność L , która ma dwa równoważne równania do wykorzystania jako definicja.

Pod względem I i Φ _B indukcyjność jest określona wzorem

${\ Displaystyle L = N {\ Frac {\ operatorname {d} \ Phi _ {B}} {\ operatorname {d} ja}}, \, \!}$

pod względem I i indukowanego emf V

${\ Displaystyle V = - L {\ Frac {\ operatorname {d} ja} {\ operatorname {d} t}}. \, \!}$

Te dwa są równoważne zgodnie z prawem indukcji Faradaya :

${\ Displaystyle V = - N {\ Frac {\ operatorname {d} \ Phi _ {B}} {\ operatorname {d} t}}, \, \!}$

${\ Displaystyle V {\ operatorname {d} t} = - N \ operatorname {d} \ Phi _ {B}, \, \!}$

zastępując w pierwszej definicji L

${\ Displaystyle L = - V {\ Frac {\ operatorname {d} t} {\ operatorname {d} ja}} \, \!} V$

$\ styl wyświetlania V = - L {\ frac {\ operatorname {d} I} {\ operatorname {d} t}} \, \!}$

więc nie wykluczają się wzajemnie.

Jedno równanie definiujące – liczba zdefiniowanych wielkości

Zauważ, że L nie może jednocześnie zdefiniować I i Φ _B - to nie ma sensu. I , Φ _B i V zostały najprawdopodobniej zdefiniowane wcześniej jako ( Φ _B podane powyżej w równaniu strumienia);

${\ Displaystyle V = {\ Frac {\ operatorname {d} W} {\ operatorname {d} q}}, \ quad I = {\ Frac {\ operatorname {d} q}{\mathrm {d} t}},\,\!}$

gdzie W = praca wykonana nad ładunkiem q . Co więcej, nie ma oddzielnej definicji ani I , ani Φ _B – ponieważ L definiuje je w tym samym równaniu.

Jednak używając siły Lorentza dla pola elektromagnetycznego :

${\ Displaystyle \ mathbf {F} = q \ lewo [\ mathbf {E} + \ lewo (\ mathbf {v} \ razy \ mathbf {B} \ prawo) \Prawidłowy],\,\!}$

jako pojedyncze równanie definiujące pole elektryczne E i pole magnetyczne B jest dozwolone, ponieważ E i B są zdefiniowane nie tylko przez jedną zmienną, ale przez trzy ; siła F , prędkość v i ładunek q . Jest to zgodne z izolowanymi definicjami E i B , ponieważ E jest definiowane za pomocą F i q :

${\ Displaystyle \ mathbf {E} = \ mathbf {F} / q. \, \!}$

i B określone przez F , v i q , jak podano powyżej.

Ograniczenia definicji

Definicje a funkcje: definiowanie wielkości może się różnić w zależności od parametrów innych niż te w definicji. Równanie definiujące określa jedynie sposób obliczania określonej wielkości, nie może opisywać, jak zmienia się wielkość w funkcji innych parametrów, ponieważ funkcja zmienia się w zależności od zastosowania. To, jak zdefiniowana wielkość zmienia się w funkcji innych parametrów, opisuje równanie lub równania konstytutywne , ponieważ zmienia się w zależności od zastosowania i od jednego przybliżenia (lub uproszczenia) do drugiego.

Przykłady

Gęstość masy ρ jest definiowana za pomocą masy m i objętości V przez, ale może zmieniać się w funkcji temperatury T i ciśnienia p , ρ = ρ ( p , T )

Częstotliwość kątowa ω propagacji fali jest określona za pomocą częstotliwości (lub równoważnie okresu czasu T ) oscylacji, jako funkcji liczby falowej k , ω = ω ( k ). Jest to zależność dyspersji dla propagacji fali.

Współczynnik restytucji dla zderzającego się obiektu jest określany za pomocą prędkości separacji i zbliżania się do punktu zderzenia, ale zależy od charakteru rozpatrywanych powierzchni.

Definicje a twierdzenia : Istnieje bardzo istotna różnica między definiowaniem równań a ogólnymi lub pochodnymi wynikami, twierdzeniami lub prawami. Definiowanie równań nie pozwala uzyskać żadnych informacji o układzie fizycznym, po prostu ponownie określa jeden pomiar w kategoriach innych. Z drugiej strony wyniki, twierdzenia i prawa dostarczają znaczących informacji, jeśli tylko w niewielkim stopniu, ponieważ reprezentują obliczenia dla wielkości przy danych innych właściwościach systemu i opisują, jak system zachowuje się, gdy zmieniają się zmienne.

Przykłady

Powyżej podano przykład dla prawa Ampere'a. Innym jest zachowanie pędu dla N ₁ początkowych cząstek o początkowym pędzie pi _gdzie i = 1, 2 ... N ₁ , oraz N _{2 końcowych} cząstek o końcowym pędzie pi (niektóre cząstki mogą eksplodować lub przylegać) gdzie j ₌ 1 , 2 ... N ₂ , równanie zachowania brzmi:

${\ Displaystyle \ suma _ {i} ^ {N_ {1}} \ mathbf {p} _ {\ rm {i}} = \ suma _ {j} ^ {N_{2}}\mathbf {p} _{\rm {j}}\,\!}$

Korzystając z definicji pędu w odniesieniu do prędkości:

${\ Displaystyle \ mathbf {p} = m \ mathbf {v} \, \!}$

więc dla każdej cząstki:

${\ Displaystyle \ mathbf {p} _ {\ rm {i}} = m_ {i} \ mathbf {v} _ {\ rm {i}} \, \!}$ i ${\ Displaystyle \ mathbf {p} _ {\ rm {j}} = m_ {j} \ mathbf {v} _ {\ rm {j}} \ \!}$

równanie zachowania można zapisać jako

${\ Displaystyle \ suma _ {i} ^ {N_ {1}} m_ {i} \ mathbf {v} _ {\ rm {i}} = \ suma _ {j} ^ {N_ {2}} m_ {i }\mathbf {v} _{\rm {i}}.\,\!}$

Jest identyczny z poprzednią wersją. Żadne informacje nie są tracone ani uzyskiwane poprzez zmianę ilości, gdy definicje są zastępowane, ale samo równanie dostarcza informacji o systemie.

Jednorazowe definicje

Niektóre równania, zwykle wynikające z wyprowadzenia, zawierają użyteczne wielkości, które służą jako jednorazowa definicja w zakresie ich zastosowania.

Przykłady

W szczególnej teorii względności masa relatywistyczna jest wspierana i odrzucana przez fizyków. Jest zdefiniowany jako:

${\ Displaystyle m = \ gamma m_ {0} \, \!}$

₀ gdzie m jest masą spoczynkową obiektu, a γ jest współczynnikiem Lorentza . To sprawia, że ​​​​niektóre wielkości, takie jak pęd p i energia E masywnego obiektu w ruchu, są łatwe do uzyskania z innych równań po prostu przy użyciu masy relatywistycznej:

${\ Displaystyle \ mathbf {p} = m \ mathbf {v} \ rightarrow \ mathbf {p} = \ gamma m_ {0} \ mathbf {v}}$

${\ Displaystyle E = mc ^ {2} \ strzałka w prawo E = \ gamma m_ {0} c ^ {2}}$

Jednak nie zawsze ma to zastosowanie, na przykład energia kinetyczna T i siła F tego samego obiektu nie są określone wzorem:

${\ Displaystyle T = {\ Frac {m} {2}} \ mathbf {v} \ cdot \ mathbf {v} \ nrightarrow T = {\ frac {\ gamma m_ {0}}{2}} \ mathbf {v} \ cdot \ mathbf {v}}$

${\ Displaystyle \ mathbf {F} = m \ mathbf {a} \nstrzałka w prawo \mathbf {F} =\gamma m_{0}\mathbf {a} }$

Czynnik Lorentza ma głębsze znaczenie i pochodzenie i jest używany w kategoriach czasu właściwego i czasu współrzędnych z czterema wektorami . Poprawne równania powyżej są konsekwencją zastosowania definicji we właściwej kolejności.

Pole magnetyczne odchylające naładowaną cząstkę, pseudookreślająca sztywność magnetyczna cząstki.

W elektromagnetyzmie naładowana cząstka (o masie m i ładunku q ) w jednorodnym polu magnetycznym B jest odchylana przez to pole po kołowym łuku spiralnym z prędkością v i promieniem krzywizny r , gdzie spiralna trajektoria jest nachylona pod kątem θ do B . Siła magnetyczna jest siłą dośrodkową , więc siła F działająca na cząstkę wynosi;

${\ Displaystyle \ mathbf {F} = - {\ Frac {m \ lewo (\ mathbf {v} \ cdot {\ mathbf {v}} \ prawej) \ mathbf {\ kapelusz {r }} }{\left|\mathbf {r} \right|}}=q\left(\mathbf {v} \times \mathbf {B} \right),\,\!}$

redukcja do postaci skalarnej i rozwiązanie dla | B || r |;

${\ Displaystyle {\ Frac {m \ lewo | \ mathbf {v} \ prawo | ^ {2}} {\ lewo | \ mathbf {r} \ prawo |}} = Q \ lewo | \ mathbf { v} \right|\left|\mathbf {B} \right|\sin \theta ,\,\!}$

${\ Displaystyle {\ Frac {m \ lewo | \ mathbf {v} \ prawo |} {\ lewo | \ mathbf {r} \ prawo |}} = Q \ lewo | \ mathbf {B} \ prawo |\sin \theta ,\,\!}$

${\ Displaystyle \ lewo | \ mathbf {B} \ prawo | \ lewo | \ mathbf {r} \ prawo | = {\ Frac {m \ lewo | \ mathbf {v} \ prawo |} {q \sin \theta }},\,\!}$

służy jako definicja sztywności magnetycznej cząstki. Ponieważ zależy to od masy i ładunku cząstki, jest przydatne do określania stopnia odchylenia cząstki w polu B , co występuje eksperymentalnie w spektrometrii mas i detektorach cząstek .

Zobacz też

• Równanie konstytutywne
• Definiowanie równania (chemia fizyczna)
• Lista równań elektromagnetyzmu
• Lista równań w mechanice klasycznej
• Lista równań w mechanice płynów
• Lista równań w grawitacji
• Lista równań w fizyce jądrowej i cząstek elementarnych
• Lista równań w mechanice kwantowej
• Lista równań fotoniki
• Lista równań relatywistycznych
• Tabela równań termodynamiki

Źródła

•   premiera Whelana; MJ Hodgeson (1978). Podstawowe zasady fizyki (wyd. 2). Johna Murraya. ISBN 0-7195-3382-1 .
•   G. Woan (2010). Cambridge Handbook of Physics Formuły . Wydawnictwo Uniwersytetu Cambridge. ISBN 978-0-521-57507-2 .
•   A. Halperna (1988). 3000 rozwiązanych problemów z fizyki, seria Schauma . Mc Graw Hill. ISBN 978-0-07-025734-4 .
•   RG Lerner ; GL Trigg (2005). Encyklopedia fizyki (wyd. 2). Wydawcy VHC, Hans Warlimont, Springer. s. 12–13. ISBN 978-0-07-025734-4 .
•   CB Parkera (1994). McGraw Hill Encyclopaedia of Physics (wyd. 2). Wzgórze McGrawa. ISBN 0-07-051400-3 .
•   PA Tipler; G. Mosca (2008). Fizyka dla naukowców i inżynierów: z nowoczesną fizyką (wyd. 6). WH Freeman and Co. ISBN 978-1-4292-0265-7 .
•   LN Ręka; JD Finch (2008). Mechanika analityczna . Wydawnictwo Uniwersytetu Cambridge. ISBN 978-0-521-57572-0 .
•   TB Arkill; CJ Millara (1974). Mechanika, wibracje i fale . Johna Murraya. ISBN 0-7195-2882-8 .
•   Ból HJ (1983). Fizyka wibracji i fal (wyd. 3). John Wiley & Synowie. ISBN 0-471-90182-2 .
•   JR Forshaw; AG Smith (2009). Dynamika i teoria względności . Wileya. ISBN 978-0-470-01460-8 .
•   GAG Bennet (1974). Elektryczność i współczesna fizyka (wyd. 2). Edwarda Arnolda (Wielka Brytania). ISBN 0-7131-2459-8 .
•   Grant IS; WR Phillips; Fizyka Manchesteru (2008). Elektromagnetyzm (wyd. 2). John Wiley & Synowie. ISBN 978-0-471-92712-9 .
•   DJ Griffiths (2007). Wprowadzenie do elektrodynamiki (wyd. 3). Pearson Education, Dorling Kindersley. ISBN 978-81-7758-293-2 .

Dalsza lektura

•   LH Greenberg (1978). Fizyka z nowoczesnymi zastosowaniami . Holt-Saunders International WB Saunders and Co. ISBN 0-7216-4247-0 .
•   JB Marion; WF Hornjak (1984). Zasady fizyki . Holt-Saunders International Saunders College. ISBN 4-8337-0195-2 .
•   A. Beisera (1987). Koncepcje fizyki współczesnej (wyd. 4). McGraw-Hill (międzynarodowy). ISBN 0-07-100144-1 .
•   HD Młody; RA Freedman (2008). Fizyka uniwersytecka - z fizyką współczesną (wyd. 12). Addison-Wesley (Pearson International). ISBN 978-0-321-50130-1 .